一种改进的LDPC码BP译码算法

郑伟，马晓越，赵成晨

(河北大学 电子信息工程学院 河北省数字医疗工程重点实验室，河北 保定 071002)



一种改进的LDPC码BP译码算法

郑伟，马晓越，赵成晨

(河北大学 电子信息工程学院 河北省数字医疗工程重点实验室，河北 保定 071002)

通过对LDPC码经典的BP译码算法进行研究，针对算法译码复杂度非常大、迭代次数多、不利于硬件实现的问题，提出了一种改进的BP译码算法.改进算法通过实时监控在连续3次迭代中译码是否稳定来减少在信噪比低于译码阈值时的迭代次数.同时，在变量消息更新过程中对传递的校验信息进行数据约束,防止由于数据溢出而导致的译码失败.仿真结果表明，改进的BP算法，在性能损失不大的情况下可以有效地降低译码的复杂度，从而更利于硬件的实现.

LDPC码；BP译码算法；迭代次数；数据约束

深空通信一般是指地球上的实体与处于月球及月球以外的宇宙空间中的航天器之间的通信，其难点是信息传输距离远，时延大，信号衰减严重.采用信道编码，尤其是高性能的信道编码可以提高信号接收能力，带来较高的编码增益，其中低密度奇偶校验码(low density parity check code,LDPC)和Turbo码就是2种优秀的信道编码，而且深空探测装置价格一般比较昂贵，为了获得较好的译码性能，往往采用复杂度较高译码算法，虽然这种算法也许只带来很少的编码增益，但这对于深空通信来说是必然的选择[1].

LDPC码是Gallager于20世纪60年代提出的一种性能接近Shannon极限的线性分组码[2].但是由于当时硬件条件和计算机条件的限制，使LDPC码在此后的很长时间内并未受到应有的重视.后来随着计算机技术的快速发展，以及众多学者重新对它进行了研究发现LDPC码与Turbo码相比具有以下优势：译码为并行迭代，运算量较低；结构并行，在硬件上易实现；码率可任意构造，灵活性更高；错误平层低，可应用于深空通信、磁盘存储工业等对误码率要求苛刻的场合；同时进一步完善了LDPC码的相关理论，使得LDPC码成为编码界继Turbo码之后最受关注的焦点.

LDPC码的译码方法主要有2种: 基于硬判决的比特翻转译码算法，简称BF算法和基于软判决的置信传播迭代译码(Belief propagation)算法，简称BP算法[3].BP算法根据消息在传递过程中的不同表现形式可以分为概率域BP算法和对数似然比(Log-likelihood Ratio,LLR)BP算法.概率域BP算法的消息用概率形式表示，相应的LLR-BP算法的消息用对数似然比表示.目前研究比较广泛的是BP译码算法和在此基础上改进的各种算法[4-9].对数域的BP算法(LLR-BP)相较于概率域的BP译码算法将大量的乘法运算变为加法运算；最小和算法(Min-Sum)减少了节点更新的计算复杂度；Normalized Min-Sum算法和Offset Min-Sum算法[10]主要用于补偿Min-Sum算法由于降低复杂度所引起的性能损失.

深空通信领域对编码增益具有较高的要求，其中BP译码算法在所有算法中译码性能最好，但是其译码复杂度比较高,不利于硬件的实现.本文针对以上问题，在BP算法的基础上提出了一种改进的BP算法，该算法通过引入校验子实时监控译码是否稳定.同时，在变量消息更新过程中对传递的校验信息进行数据约束，防止由于数据溢出而导致的译码失败.通过实验仿真表明，改进的算法能够在译码性能损失不大的情况下，降低译码复杂度，易于硬件实现.

1 LDPC码

LDPC码是一种具有稀疏性的线性分组码，所谓稀疏性是指校验矩阵中只有数量很少的元素为“1”，大部分都为“0”.LDPC码可以用校验矩阵H表示，若H的维数为(m,n)且为满秩，那么LDPC码的码长为n，信息位为前k=n-m个，校验位为后m个.LDPC码一般可以表示为(n,k)，其码率为R=k/n.

LDPC码可以由其校验矩阵H唯一确定，式(1)、(2)为(8，2，4)LDPC码的校验矩阵，从式(1)、(2)看出H矩阵的行重和列重分别为4和2.

(1)

对应的校验方程式

(2)

除了用矩阵形式来表示LDPC码外，利用Tanner图表示也是一种较为方便的方法，它可以生动形象地描述LDPC码的编译码的性能.Tanner图是一种双向图，可用节点的集合来表示.其中，H矩阵的行向量对应Tanner图中的校验节点；H矩阵的列向量对应于Tanner图中的变量节点.式(1)所示校验矩阵对应的Tanner图如图1所示，c1～c4表示校验节点，v1～v8表示变量节点.

2 BP译码算法

BP译码算法的主要思想就是在每一次的迭代过程中，利用从信道中接收到的信息，通过在变量节点和校验节点之间不断地进行信息的传递和迭代运算进行译码.BP算法的大致过程包括：初始化、信息处理和硬判决，其中信息的处理过程包括校验节点的信息处理和变量节点的信息处理.

图1 (8，2，4)LDPC码的Tanner图Fig.1 (8,2,4)Tanner graph of the LDPC codes

在信息传输的过程中，信道编码后得到二进制码字序列x=(x1,x2,…，xn)，该序列采用BPSK调制y=2x-1映射为y=(y1,y2,…，yn)，然后再输入高斯白噪声(AWGN)信道后得到输出序列z=(z1,z2,…，zn).在译码过程中，为简单定义如下：c=(c1,c2,…，cn)为译码得到的序列；rij(x)(x=0,1)表示校验节点j传递给变量节点i的信息；qij(x)(x=0,1)表示变量节点i传递给校验节点j的信息；R(j)表示与校验节点j相连的变量节点i的集合.C(i)表示与变量节点i相连的校验节点j的集合；R(j)/i表示除i外与校验节点j相连的变量节点的集合；C(i)/j表示除j外与变量节点i相连的校验节点的集合.

BP译码算法的大致步骤如下.

1)初始化

在已知信道先验知识的情况下，计算信道传递给变量节点的初始概率Pi(1)=P(xi=1)和Pi(0)=1-Pi(1)(i=1,2,…，n)，然后设定变量节点i传向校验节点j的初始消息：

qij(0)=Pi(0),

(3)

qij(1)=Pi(1).

(4)

2)校验节点的信息处理 计算变量节点传向校验节点的后验概率.

(5)

(6)

3)变量节点的信息处理 由校验节点的后验概率计算变量节点的后验概率.

利用步骤2)的rij(0)和rij(1)更新qij(0)和qij(1)，其计算公式为

(7)

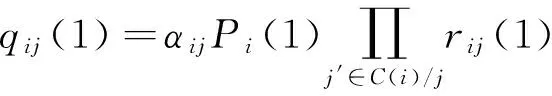
(8)

其中，αij为校正因子，满足qij(0)+qij(1)=1.

4)硬判决 对所有变量节点计算硬判决信息为

(9)

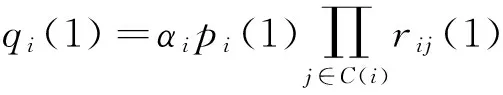
(10)

其中，αi为校正因子，满足qi(0)+qi(1)=1.

根据判决条件做出硬判决，当qi(1)>qi(0)时，令ci=1；反之令ci=0.得到全部译码输出序列c.若此时满足

HcTmod 2=0，

(11)

则译码停止，否则继续进行上述步骤，直至达到预先设定最大迭代次数，译码结束.BP译码算法流程图如图2所示.

图3为BP、LLR-BP、Min-Sum 3种不同译码算法性能比较，仿真中利用IEEE802.16e标准LDPC码的校验矩阵的准双对角线结构进行快速编码，再分别利用上述3种不同算法进行译码，其中选用的码长为580，码率为R=1/2，迭代次数为15.从图3可以看出，BP算法、LLR-BP算法、Min-Sum算法的译码性能是依次降低的，3种算法在相同信噪比(Signal-noise ratio,SNR)的情况下，误码率(bit error rate,BER)依次升高，这是因为LLR-BP算法是BP算法在对数域的计算，Min-Sum是在对数域的基础上取近似，故译码性能依次降低.由于在深空通信领域对译码性能要求比较高，故本文选用BP算法进行研究和改进.

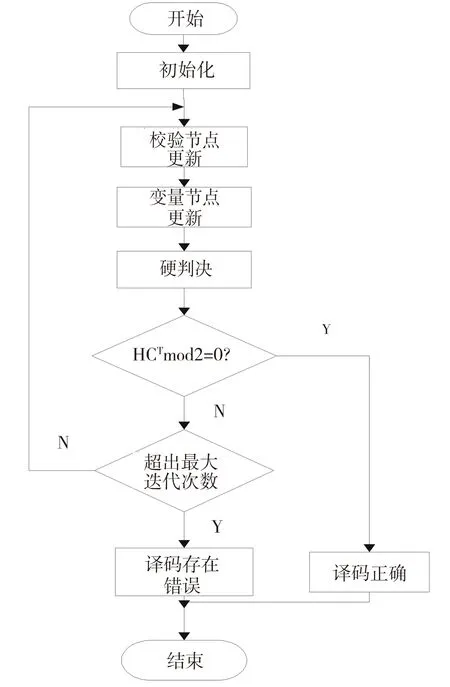
图2 BP译码算法流程Fig.2 Flowchart of BP decoding algorithm

图3 BP、LLR-BP、Min-Sum译码算法性能比较Fig.3 Comparison of BP，LLR-BP，Min-Sum decoding algorithm performance

3 改进的BP译码算法

当信道中信噪比较低时，随着迭代次数的增加节点之间交换的有效信息越来越少，当迭代达到一定次数后，节点之间不再交换有效信息，再增加迭代次数并不能使误码率降低，即迭代次数不需要达到最大就可使译码输出的误码率稳定，因此，需要设置终止准则来停止译码.本文通过引入校验子在连续3次迭代过程中是否稳定来判定是否结束循环[6，11].现定义校验子为z=HcTmod2，在每次迭代过程中，若式(11)满足条件，则表示译码正确；若式(11)不满足条件的话，判断校验子在连续3次迭代过程中非零元素的数目是否保持不变,若不变，则译码错误停止迭代；若变化，则继续进行迭代，直到达到最大迭代次数.

同时考虑到在信息传递过程中有很多接近0的小数存在，故在进行连乘等运算时很容易出现数据的溢出，导致译码失败，故改进的算法在上述的基础上加入了数据约束[12].在变量节点更新过程中存储的浮点信息均为单精度32位的浮点数，即在式(7)、(8)校验节点信息乘积过程中产生的浮点数很容易超出32位的表示范围，使数据溢出，导致译码失败.针对此问题，在进行乘积之前对rij(0)和rij(1)进行数据约束：若rij(0)和rij(1)的绝对值小于10-N则令其为10-N，以保证相乘的信息在其表示范围内，从而避免了数据溢出的问题.改进BP算法的程序流程如图4所示.

图5为当N取不同值时对BP算法性能的影响，从图5中可以看出，加入数据约束后的译码性能稍有降低，但由于对数据进行了约束，才能有效地防止数据溢出，保证译码的正确性.当为4时译码性能最接近BP算法，故取10-4作为数据约束值.

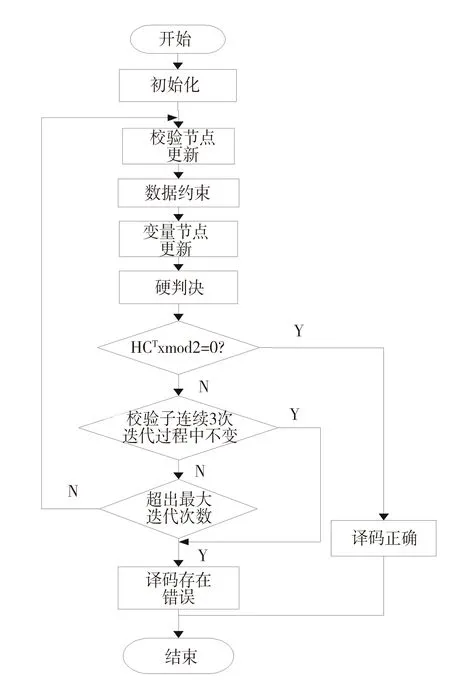
图4 改进BP译码算法流程Fig.4 Flowchart of improvement BP decoding algorithm

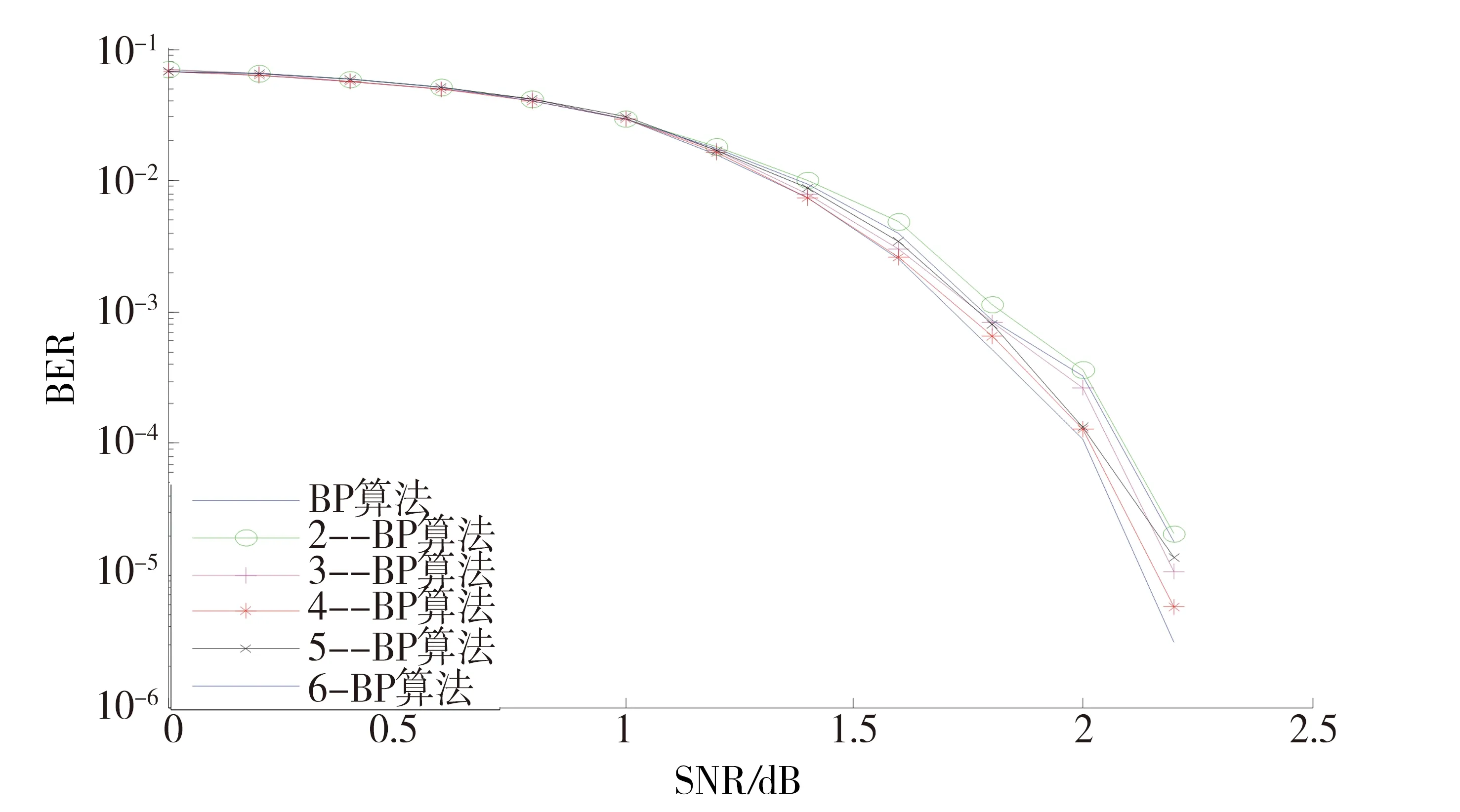
图5 N的不同取值对译码性能的影响Fig.5 Effect of different values of N on decoding performance

4 性能仿真

为了验证码长对译码算法性能的影响，在迭代次数固定为30时，分别选用码长为150、310、630、1 270的LDPC码进行仿真，实验结果如图6所示.从图6可以看出，码长为150的LDPC码译码性能最差，码长为1 270的LDPC码译码性能最好，即在相同码率与迭代次数的情况下，随着码长的增加，LDPC码的译码性能越来越好.

为了验证迭代次数对译码性能的影响，在码长固定为1 270时，选用不同迭代次数对译码性能进行比较，实验结果如图7所示.从图7可以看出，当迭代次数为5时，译码性能最差，随着迭代次数的增加曲线的收敛速度越快，译码性能越好，即在相同码率与码长的情况下，随着迭代次数的增加，译码性能越来越好.

为了验证改进BP算法的性能，以matlab作为实验平台进行仿真，仿真选用的是IEEE802.16e标准中的码长为1 270，码率为R=1/2的规则LDPC码.图8为改进的BP算法、原始BP算法、文献[6]BP算法3者译码性能比较，图9为3者迭代次数比较.

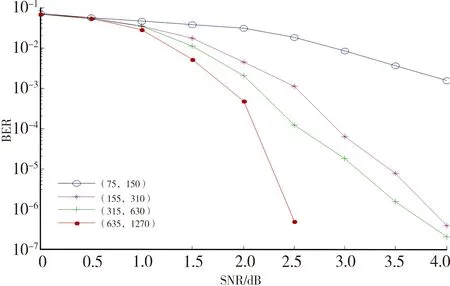
图6 码长对译码性能的影响Fig.6 Effect of code length to decoding performance

图7 迭代次数对译码性能的影响Fig.7 Effect of iterations to decoding performance

从图8可以看出，当处于较低SNR条件下时，改进的BP算法与上述2种算法的收敛速度几乎完全一致，而当SNR较高时，改进BP算法收敛速度相比于其他2种算法稍有下降.

从图9可以看出当信噪比较低时，改进BP算法与文献[6]BP算法的迭代次数相同且比原始BP算法相比有大幅的下降；当信噪比较高时,改进BP算法与原始BP算法的迭代次数相同且比文献[6]BP算法的低.所以改进的BP算法能够以较低的迭代次数满足性能的要求，从而在译码性能和复杂度上取得一个良好的折衷.

图8 3者译码性能比较Fig.8 Three decoding performance comparison

图9 3者迭代次数比较Fig.9 Comparison of three methods of iterations

5 结束语

经过仿真验证,本文提出的LDPC码的改进BP译码算法相对于原始的BP译码算法,可以降低在信噪比较低的条件下的译码迭代次数，同时有效地防止了由于数据溢出导致的译码失败.BP译码算法的迭代次数的多少和译码的正确与否直接影响着其实际应用.改进的算法在保证译码性能和译码正确性的前提下，降低了译码的复杂度，在一定程度上解决了硬件难以实现的问题，尤其对于深空通信中信噪比较低的情况下改进的算法具有一定的应用价值.

[1] 窦金芳，王楠，周宇昌，等.LDPC码在深空通信中的应用[J].遥测遥控，2009，30(1):30-34. DOU J F，WANG N，ZHOU Y C,et al.Application of LDPC codes in the deep space communication[J].Journal of Telemetry，Tracking and Command，2009,30(1):30-34.DOI:10.13435/j.cnki.ttc.002191.

[2] GALLAGER R G. Low-density parity-check code[J].IRE Transactions on Information Theory,1962,8(1):21-28.DOI:10.1109/TIT.1962.1057683.

[3] 刘明山，王亚忠，刘珊珊.LDPC码改进型LBP译码算法研究[J].吉林大学学报(信息科学版),2015,33(4):367-372.DOI:10.3969/j.issn.1671-5896.2015.04.004. LIU M S，WANG Y Z，LIU S S.Research on modified LBP decoding algorithm of LDPC codes[J].Journal of Jilin University(Information Science Edition),2015,33(4):367-372.DOI:10.3969/j.issn.1671-5896.2015.04.004.

[4] CHEN J，FOSSORIER M.Density evolution for two improved BP-based decoding algorithms of LDPC codes[J].IEEE on Communication Letters,2002,6(5):208-210.DOI:10.1109/4234.1001666.

[5] WANG L A，LIU X.Improved BP decoding Algorithm for LDPC codes[J].Advanced Materials Research，2013,846-847: 925-928.DOI:10.4028/www.scientific.net/AMR.846-847.925.

[6] 郭永富，周傲松.一种改进的LDPC码BP译码算法[J].宇航学报,2009,30(1):240-243.DOI:10.3873 j.issn.1000-1328.2009.00.042. GUO Y F,ZHOU A S.An improved BP decoding algorithm of LDPC codes[J].Journal of Astronautics,2009,30(1): 240-243.DOI:10.3873 j.issn.1000-1328.2009.00.042.

[7] 李秀花，高永安，马雯.LDPC码译码算法及性能分析[J].现代电子技术，2014，37(1):1-4.DOI:10.3969/j.issn.1004-373X.2014.01.001. LI X H，GAO Y A，MA W.Decoding algorithm and performance analysis of LDPC codes[J].Modern Electronics Technique,2014,37(1):1-4.DOI:10.3969/j.issn.1004-373X.2014.01.001.

[8] ZHANG Q H,ZHANG J W,BAO J R.FPGA-Based improved decoding algorithm of LDPC codes[J].Applied Mechanics and Materials,2014,519-520:993-997.DOI:10.4028/www.scientific.net/AMM.519-520.995.

[9] SUN Z Y，LI H H.Improvement of LDPC codes decoding algorithm in the application of the rotational OFDM system[J].Advanced Materials Research,2014,934:235-238.DOI:10.4028/www.scientific.net/AMR.934.235.

[10] ZHAO J,ZARKESHVARI F，BANIHASHCMI A H.On implementation of min-sum algorithm and its modifications for decoding Low-density parity-check(LDPC)codes[J].IEEE Transactions on Communications,2005,53(4):549-554.DOI:10.1109/TCOMM.2004.836563.

[11] 孙斌，王钢，杨文超，等.一种改进型LLR BP算法的LDPC译码研究[J].无线电工程，2015，45(3):4-6,18.DOI:10.3969/j.issn.1003-3106.2015.0302. SUN B，WANG G，YANG W C,et al.A new modified LLR BP algorithm research for LDPC decoders[J].Radio Engineering,2015,45(3):4-6,18.DOI:10.3969/j.issn.1003-3106.2015.0302.

[12] 张霖，赵旦峰，薛睿，等.基于BP算法的QC-LDPC译码器的DSP实现[J].应用科技，2011，38(3):34-37.DOI:10.3969/j.issn.1009-671X.2011.03.008. ZHANG L，ZHAO D F，XUE R,et al.The DSP implementation of QC-LDPC decoder based on BP algorithm[J].Applied Science and Technology,2011,38(3):34-37.DOI:10.3969/j.issn.1009-671X.2011.03.008.

(责任编辑：王兰英)

An improved BP decoding algorithm of LDPC codes

ZHENG Wei,MA Xiaoyue,ZHAO Chengchen

(Key Laboratory of Digital Medical Engineering in Hebei Province Electronic Information Engineering College,Hebei University,Baoding 071002,China)

In BP decoding algorithm of LDPC codes decoding algorithm complexity is usually very high，more iterations is not conducive to the realization of hardware.We proposed an improved BP decoding algorithm.The improved decoding algorithm for real-time monitoring through three consecutive iterations is stable to reduce the number of iterations in the decoding when the SNR is below the threshold value，at the same time the variable message updates to check information transmission constraints.Simulation results demonstrate that the improved BP algorithm，in the case of almost no performance loss,can effectively reduce the complexity of decoding，thus more conducive to the realization of the hardware.

LDPC codes;BP decoding algorithm;iterations;data constraints

10.3969/j.issn.1000-1565.2016.05.016

2015-12-05

河北大学医工交叉研究中心开放基金项目(BM201103)

郑伟(1972—)，女，黑龙江兰西人，河北大学教授，博士，主要从事图像处理、图像安全通信的研究． E-mail:147685650@qq.com

TN911

A

1000-1565(2016)05-0547-07