混合Markov与Bayes的客户欠费预测模型

吴舒霞，陈炼，高胜保

(1.南昌大学 信息工程学院，江西 南昌 330031；2.中国电信股份有限公司 江西分公司，江西 南昌 330029)



混合Markov与Bayes的客户欠费预测模型

吴舒霞1，陈炼1，高胜保2

(1.南昌大学 信息工程学院，江西 南昌 330031；2.中国电信股份有限公司 江西分公司，江西 南昌 330029)

为有效规避客户欠逃费和实现差异化处置，针对具有长期定时付费特征的后付费类服务，提出混合马尔科夫与贝叶斯的客户欠费预测模型，基于全客户多要素信息增益分析，给出潜在欠费客户的欠费概率，为客户欠费预警和处置提供全面、客观、精细的决策信息，并支持客户差异化处置.首先，基于其付费特点，建立k序马尔科夫模型，计算客户的初始欠费概率；然后，融合客户基本属性、行为特征和欠费信息等要素，基于条件互信息和爬山法生成目标贝叶斯网络，对初始欠费概率予以修正，形成客户最终欠费概率；最后，基于实际数据进行实证分析，验证了该模型的有效性.

后付费客户；欠费预测模型；混合马尔科夫；贝叶斯

中国服务业的迅速发展，使得人们的工作、生活更为快捷、便利.然而，对于各种具有长期使用定时付费特征的后付费型服务(如电信、电力、煤气等)的欠逃费现象也日益增加，造成服务企业的经济损失与资产流失，增加其运营成本，影响企业的业务发展，导致企业难以向社会提供更优质的服务.为有效解决上述问题，可以基于服务企业积累的海量数据，从中挖掘欠费行为的潜在规律及其主要影响因素，应用各种数据分析工具，构建数学预测模型，对客户的欠费可能性进行预测分析.目前，国内关于欠费预测模型的可参考文献很少.文献[1]通过贝叶斯和关联规则算法，对已有住院病人欠费现象进行分析，提出了住院病人欠费预测模型，给出其欠费概率；此模型基于历史数据，分析影响欠费的重要属性并根据现实场景予以调整，能够较好地规避一次性的欠逃费行为，但其不适用于长期定时付费型服务.文献[2]提出基于决策树算法的电信客户欠费预测模型，可以预测长期定时付费型服务的欠费客户，但仅依据历史客户欠费行为数据预测新增客户是否欠费和提供二值结果(欠费/不欠费)，而不是欠费概率.文献[3]提出了基于SVM的电信客户欠费分析模型，基于客户的行为分析，通过多项式核函数对客户进行欠费预测分析，能够获得较好的效果，其主要不足：1)仅用于预测分析已经欠费停机的客户是否会继续欠费；2)仅提供二值结果(欠费/不欠费)，而不是欠费概率.

综上，文献[2]和文献[3]一方面都仅侧重于对特定欠费客户的分析，存在客户局部性的不足；他们都仅给出二值结果(欠费/不欠费)，无法支持客户的差异化处置.文献[1]虽然给出了全体客户预测分析的欠费概率，但其仅使用已发生欠逃费病人的局部数据进行分析，而不是全部病人的全类型数据，并且仅适用于规避一次性的欠、逃费行为，不适用于长期定时付费型服务.为此，本文针对长期定时付费特征的后付费型服务，提出混合马尔科夫和贝叶斯的欠费预测模型HMBPM (prediction model of customer arrears based on hybrid Markov and Bayesian).该模型基于海量历史数据，融合客户基本属性、行为特征和欠费信息等多要素进行综合信息增益分析，给出潜在欠费客户的欠费概率.由此，就可以为客户欠费预警和处置提供更为全面、客观、精细的辅助决策信息，从而对其予以重点关注和处置，以有效地规避欠逃费行为；依据潜在欠费客户的欠费行为分析与欠费概率，可以针对性地采取差异化处置措施，从而优化客户感知，降低处置成本；通过分析数据，有助于企业提升服务质量和管理水平.主要工作：1)根据历史数据中欠费的状态转移情况，构建k序马尔科夫模型，计算客户的初始欠费概率；2)利用条件互信息和爬山法生成目标贝叶斯网络；3)对生成的目标贝叶斯网络进行学习，计算其边缘概率和条件概率，修正初始欠费概率，生成客户的最终欠费概率；4)基于电信运营商的实际数据进行实证分析，验证HMBPM模型的有效性.

1 HMBPM预测模型

1.1 数据定义

对于欠费问题的描述，通常从客户属性出发来评估客户的欠费行为，包括：客户的信用额度、开户时间、平均月消费、欠费次数、欠费原因、欠费金额、平均欠费时长，等.客户未欠费或者欠费金额在信用额度以内则称之为正常客户，否则为欠费客户，两者分别用C1和C2表示.假设使用m个指标数据为n个欠费客户给出评价，其中Xi表示客户的属性，Ci表示第i个客户的客户类型，Ci=1表示该客户属于正常客户，Ci=2表示该客户为欠费客户.样本集为G={(Xi,Ci)|i=1,2,…，n}，之后需要解决的问题就是如何根据已知数据，分析出哪些是正常客户哪些是欠费客户.

1.2 k序马尔科夫预测模型

基本马尔科夫模型的状态迁移过程中,从状态ii迁移到ii+1仅取决ii，而与ii-1及其之前的状态无关,而实际应用场景非常复杂，从ii到ii+1的迁移一般都与ii-1及其之前更多的状态相关.鉴于HMBPM必须考虑ii+1之前的k(k>1)个状态，才能保证预测的准确率，因而必须使用k序马尔科夫模型[4]，对客户进行预测，判断该客户下一时刻的欠费倾向.此时，k值的选择至关重要：一般而言，预测准确率正比于k的取值，但其计算复杂度也正比于k；若k值取得太小，却会由于样本的减少导致不能获得理想的预测准确率，故必须综合权衡计算复杂度和准确率，选取适当的k值.

第1步，构建基本马尔科夫模型.C={c1,c2,…，cn}为所有客户的集合，状态I={i1,i2,…，in}为所有状态的集合，则条件概率P(in+1|in,in-1,…,i1)表示此前状态分别为i1,i2,…，in的客户转移到下一状态in+1的概率.于是，基于基本马尔科夫模型对的in+1预测可以表示为

in+1=arg max{P{in+1|in,in-1,…,i1}}=argmax(P{in+1|in})，

(1)

其中，in表示客户在第n时刻的状态，则要预测在n+1时刻客户的状态，就要计算出条件概率P(in+1|in)值最大时的客户状态，即为此客户n+1时刻的状态[5].

第2步，构建k序马尔科夫预测模型.主要思想是“客户下一时刻的状态仅与最近的k个状态有关”，即下一时刻的预测与较近时刻的状态具有较强相关性，时间距其越远，则相关性随之递减,于是公式(1)可以表示为

in+1=argmax{P{in+1|in,in-1,…，i1}}=argmax{P{in+1|in,in-1,…，in-k+1}}.

(2)

第3步，计算该客户此前k个状态中分别为in,in-1,…，in-k+1的频数，结果记作S(in,in-1,…，in-k+1.根据似然估计法可知：P(in+1|in,in-1,…,in-k+1)，可表示为

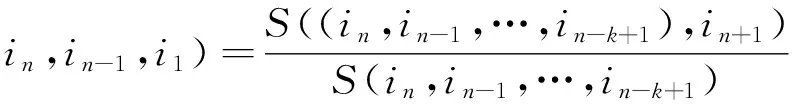
(3)

其中S((in,in-1,…，in-k+1),in+1)表示客户的前k个状态分别为in,in-1,…，in-k+1，并且下一状态为in+1的频数.

基于以下原因，HMBPM需要进一步引入贝叶斯网络对客户欠费概率进行修正.1)k序马尔科夫模型仅给出是否欠费的预测概率，无法深入分析客户欠费的原因，特别当样本状态数较少时，其正确率较低.2)计算每个客户的欠费概率时，其值有可能趋近0.5，导致进入判定客户是否欠费的模糊区.

1.3 基于贝叶斯的概率修正

1.3.1 事件因子提取

造成欠费的原因有很多，需要在众多的属性中提取符合恶意欠费判断条件的属性[6].需要考虑的属性可以分成动态属性和静态属性，静态属性一般是客户的基本资料，动态属性一般是客户欠费金额、平均月消费、付费时间等.以下采取多元逻辑回归的方式提取相关属性.定义：

P=β0+β1X1+β2X2+…+βmXm，

(4)

其中，客户X={X1,X2,…，Xm},Xi(i<=m)表示客户的属性.当P≤α时，属性变量对决策属性有很大影响；反之，该属性变量与决策属性无关.最终得到N个属性值，用于全面估计客户的欠费概率.

1.3.2 数据离散化

在上述N个属性值中，很多属性为数值型，而贝叶斯网络需要的数据是离散化数据，从而需要进行离散化处理.为此，采用等频率划分算法，根据给定的参数k将m个对象分成段,每一段中有m/k个对象.然后，将相关属性在所有实例上的取值按从小到大进行排列,每隔m/k取值作为一个断点段.参数k可以选取业务人员的经验值,以保证离散化的结果能够更真实地反映出数据的分布情况.离散化结果如表1，其中是否欠费属于决策属性，其余为条件属性.

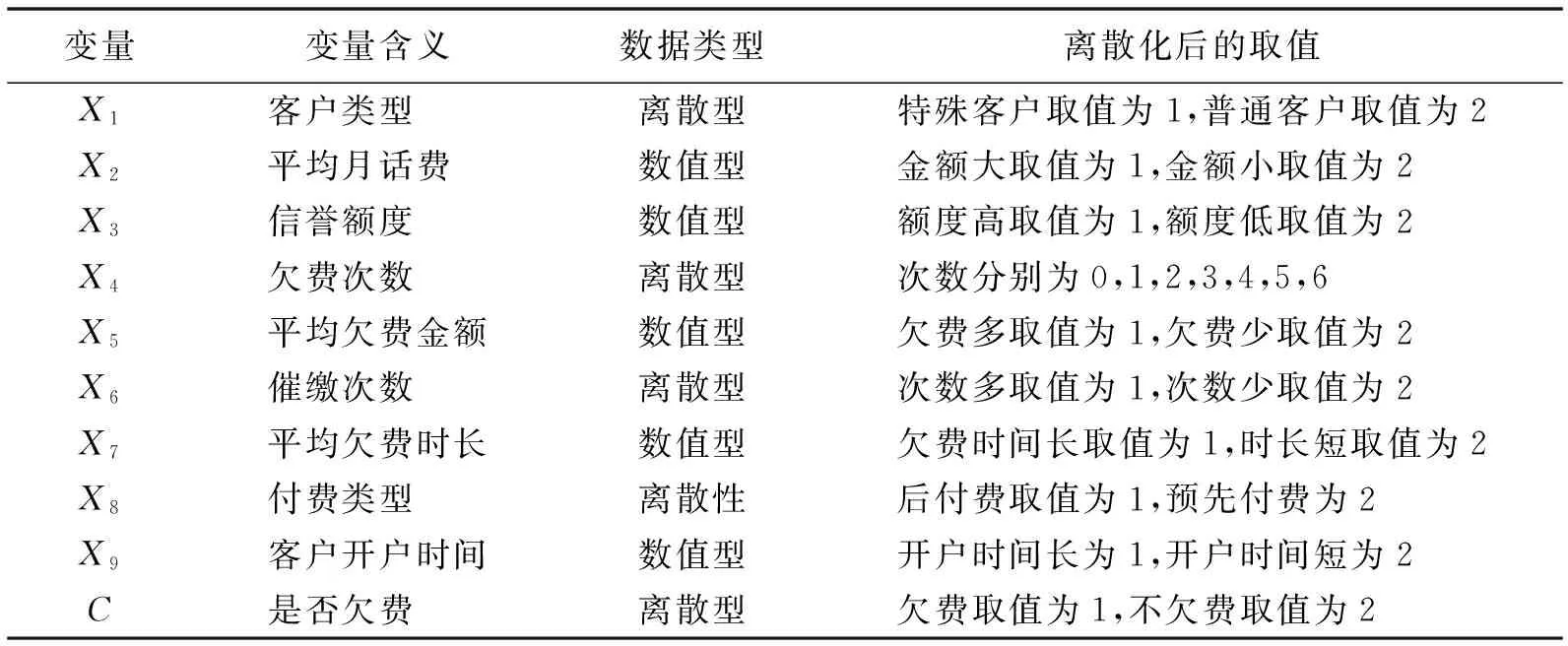
表1 客户属性值离散化处理

1.3.3 基于互信息和爬山法的贝叶斯计算

1)应用互信息公式计算事件因子与XiXj之间的条件概率依赖值生成无向图.如果两者的互信息值大于某个阈值，即MI(Xi,Xj,Ck)>ε,则二者之间存在一条边，否则两者之间相互独立，即不存在边；

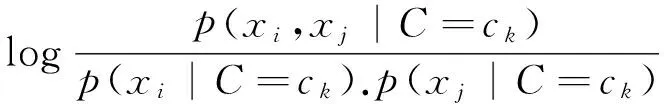
(5)

2)确定无向图中边的方向:为使贝叶斯网络中不存在回路和环，假定方向由编号小的属性指向编号大的属性[7]，生成原始贝叶斯网络；

3)应用爬山算法采用加边、减边、转边的方法进行搜索，比较贝叶斯网络的评分函数值的高低，选取其中分值最高者作为目标贝叶斯网络，相应的贝叶斯评分函数[8-9]如下：

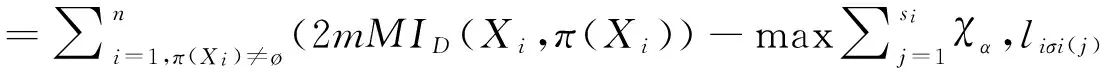
(6)

其中，MID(Xi,π(Xi))表示Xi与其父节点之间的互信息，si为Xi的父节点的个数，χα,liσi(j)表示置信度为α自由度为liσi(j)的卡方分布值.

4)预测客户的欠费概率P2：通过对目标贝叶斯网络的学习，计算各个节点与父节点之间的条件概率值和边缘概率值，通过公式(7)[10]计算客户的欠费概率P2.

|π(Xi)),

(7)

其中Xi(i=1,2,…，n)表示贝叶斯网络中的节点，π(Xi)表示Xi节点的父节点集.

5)计算客户的欠费概率：经过k序马尔科夫模型计算得到初始欠费概率P1，使用贝叶斯网络进行概率修正得到欠费概率P2.对两者进行加权相加可得最终概率为P=ω1p1+ω2p2，则不欠费概率为1-P，其中ω1+ω2=1.

2 实证分析

本文实验数据来源于某电信分公司的计费系统和欠费催缴系统，时间跨度6个月.其中，客户欠费情况如表2；客户欠费详细数据见表3，包括以下属性值：客户开户时间、客户类型、月平均话费、信誉额度、欠费次数、平均欠费金额、催缴次数、平均欠费时长、付费类型、是否欠费.随机抽取10 000条数据作为训练数据.决策属性用y=1表示正常客户，y=2表示欠费客户.最近6个月欠费情况如表2、表3.

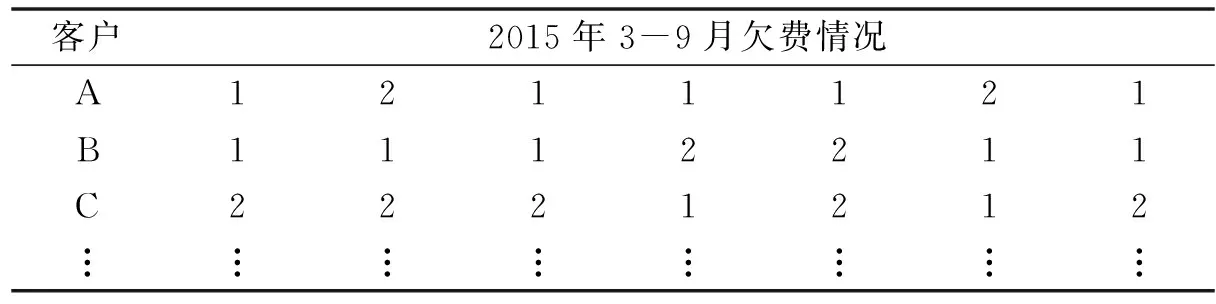
表2 客户最近6个月欠费情况

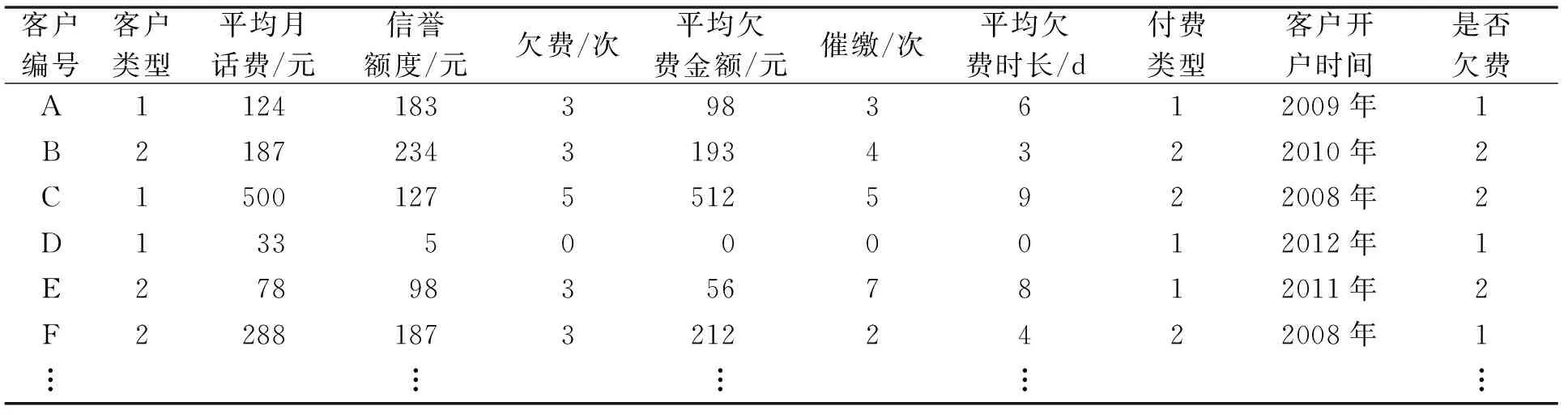
表3 客户欠费详单

1)基于6个月欠费数据，利用k序马尔科夫模型计算出客户的欠费概率P1.

2)对客户属性数据预处理，包括：分析出影响决策属性的重要属性，删减不重要的属性值以及对数值型属性进行离散化.

3)将客户属性作为训练集，利用互信息和爬山法得出评分函数评分值最高的目标贝叶斯网络.目标贝叶斯网络结构图如图1.

4)基于目标贝叶斯网络，构建属性条件概率依赖表，然后计算客户的欠费概率P2.

5)利用欠费概率P2对欠费概率P1进行加权修正，公式为P=ω1p1+ω2p2.

6)通过对后一个月的数据和HMBPM模型预测结果进行比较，计算HMBPM模型的准确率，对HMBPM模型有效性进行分析和验证，结果如图2.其中ω1=0.3，ω2=0.7.为了进一步了解权重系数对模型的影响，比较ω1不同取值的准确率,结果如图3.

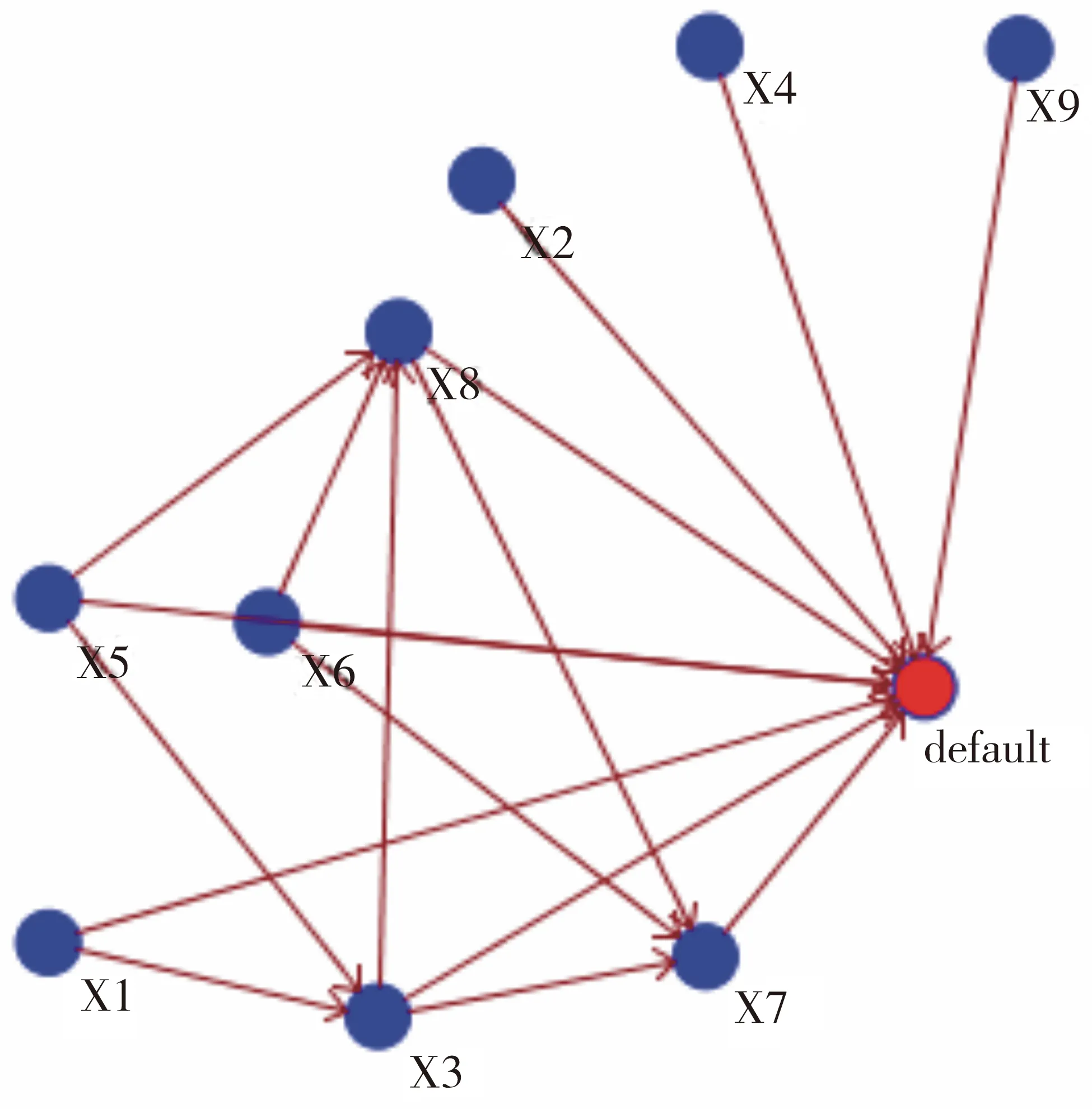
图1 目标贝叶斯网络Fig.1 Final Bayesian network

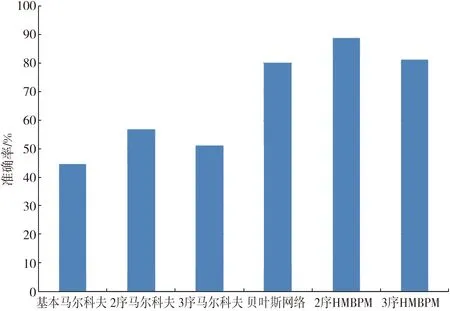
图2 各个模型准确率比较Fig.2 Comparison of every model’s accuracy

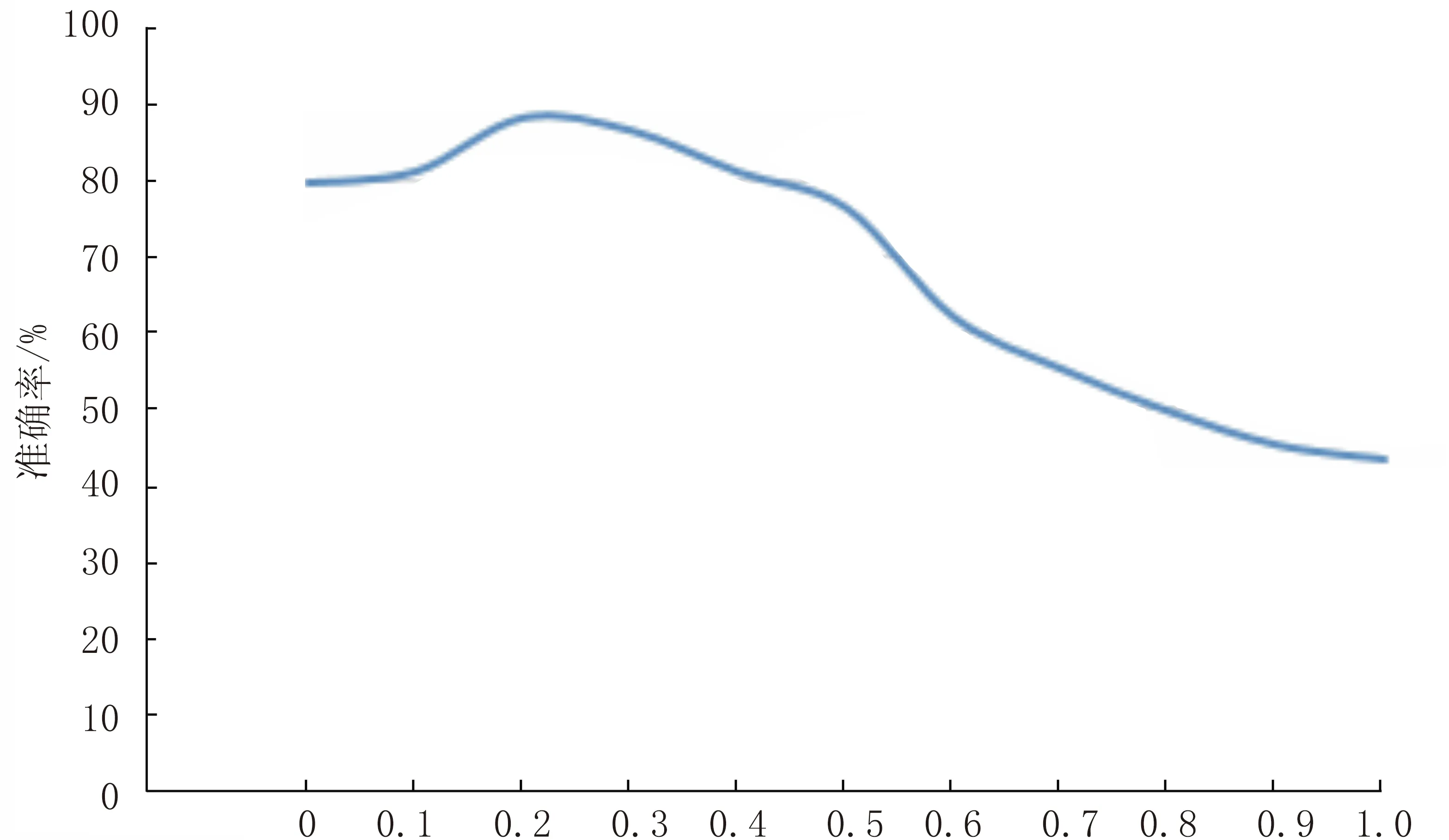
ω1的取值图3 ω1不同取值下模型准确率比较Fig.3 Comparison of the model’s accuracy under the different ω1

结论1：HMBPM在准确率上高于单一的马尔科夫模型或贝叶斯网络模型.

结论2：基本马尔科夫模型、2序马尔科夫模型、3序马尔科夫模型，准确率先上升然后有一定程度上的下降.2序的HMBPM和3序的HMBPM准确率相当，综合考虑准确率和计算复杂度，一般宜采用2序HMBPM.

结论3：ω1和ω2不同的取值对HMBPM有一定的影响，若ω1取值较大时，准确率接近于马尔科夫模型，ω2取值较大时接近于贝叶斯网络模型.同时ω1取值为0.2附近时，模型准确率达到峰值.

3 结束语

对于各种具有长期定时付费特征的后付费类服务，急需潜在欠费客户的全面、客观、精细的欠费概率信息，以有效规避欠逃费行为，通过差异化处置优化客户感知并降低处置成本，提升企业服务质量和管理水平.为此，本文针对已有各种欠费预测模型的局限性与不足，基于全客户多要素信息增益分析的思路，提出了混合马尔科夫和贝叶斯的欠费预测模型HMBPM，并基于实际数据进行实证分析，验证了该模型的有效性.

[1] 李斌杰.住院病人的欠费预测模型研究[J].中国数字医学，2010,26(12):60-62.DOI:10.3969/j.issn.1673-7571.2010.012.019. LI B J.The research of inpatient delinquency forecasting model[J].Health Information Forum.2010,26(12):60-62.DOI: 10.3969/j.issn.1673-7571.2010.012.019.

[2] 王栋，董理，占守义.基于分类技术的电信欠费预测模型[J].计算机工程与应用,2003,38(7):123-125. WANG D，DONG L，ZHAN S Y.Owing fee model in telecommunication based on classifying[J].Computer Engineering and Appliations,2003,38(7):1123-125.

[3] 李学鹏,张国基.基于支持向量机的电信欠费客户分析模型[J].计算机应用,2006,5(12): 214-215.

[4] 李玉华，李栋才，毕威，等.混合马尔科夫预测模型及其在反洗钱中的应用研究[J].计算机科学.2011,38(7):170-174. LI Y H，LI D C，BI W,et al.Hybrid Markov prediction model and research of application in anti-money laundering[J].Computer Science,2011,38(7):170-174.

[5] DERRODE S，PIECZYNSKI W.Unsupervised classification using hidden Markov chain with unknown noise copulas and margins[J].Signal Processing，2016,128:8-17.DOI:10.1016/j.sigpro.2016.03.008.

[6] 郑莉华，陈佳.基于贝叶斯网络的电信话费欺诈的模型研究及应用[J].计算机应用,2008,28(2):510-512. ZHENG L H ,CHEN J.Research and application of telecom charge fraudulent model based on Bayesian network[J].Computer Applications,2008,28(2):510-512.

[7] 金焱，胡云安,张瑾,等.互信息和爬山算法相结合的贝叶斯结构学习[J].计算机应用与软件,2012,29(9): 122-125.DOI:10.3969/j.issn.1000-386x.2010.09.032. JIN Y，HU Y A，ZHANG J,et al.Bayesian network structure learning combining mutual information with hill climbing algorithm [J].Computer Applications and Software,2012,29(9): 122-125.DOI:10.3969/j.issn.1000-386x.2010.09.032.

[8] GHEISARI S，MEYBODI M R.BNC-PSO: structure learning of Bayesian networks by particle swarm optimization[J].Information Sciences，2016，348:272-289.DOI:10.1016/j.jns.2016.01.090.

[9] 朱明敏.贝叶斯网络结构学习与推理研究[D].西安：西安电子科技大学，2013. ZHU M M.Research on structural learning and inference in Bayesian networks[D].Xi′an:Xidian University,2013.

[10] JIANG J，WANG J，YU H，et al.Poison identification based on Bayesian network: A novel improvement on K2 algorithm via Markov blanket[J].Lecture Notes in Computer Science,2013:173-182.DOI:10.1007/978-3-642-38715-9-21.

(责任编辑：孟素兰)

A prediction model of customer arrears based on hybrid Markov and Bayesian

WU Shuxia1，CHEN Lian1，GAO Shengbao2

(1.Information Engineering College,Nanchang University,Nanchang 330031,China；2.Jiangxi Branch of China Telecom Co,Nanchang 330029,China)

In order to analyze the post-paid services with the characteristics of long term and on time pay，we put forward a prediction model based on hybrid Markov and Bayesian. It is based on the multi-factor information gain of all the customers，and computes the potential owe customers' probability of arrears.Moreover，it can provide comprehensive，objective and subtle decision information to the warning of customer arrears and disposal，and it can support differentiation treatment.First of all，we build the k-order Markov model based on the characteristics of the pay，then calculate the customers' initial probability.Secondly，we merge the customers' basic attributes，behavior feature and own information.Then，using the conditional mutual information and the hill climbing algorithm to generate the target Bayesian network to modify the initial probability of arrears，which form the final client own probability.Finally，through experiment by using the real data,we prove that this predict model is efficient in customer prediction.

post-paid customer；probability prediction model；hybrid Markov；Bayesian

10.3969/j.issn.1000-1565.2016.05.014

2016-02-29

国家自然科学基金资助项目(61463033)；江西省教育厅科学技术研究项目(GJJ14136)

吴舒霞(1991—)，女，江西南昌人，南昌大学在读硕士研究生.E-mail:352901867@qq.com

TP181

A

1000-1565(2016)05-0535-06