激光辐照材料表面非Fourier热传导问题的半解析解

张丽静，尚新春

(北京科技大学 数理学院，北京 100083)



激光辐照材料表面非Fourier热传导问题的半解析解

张丽静，尚新春

(北京科技大学 数理学院，北京 100083)

针对有较长热驰豫时间的材料在表面受到激光脉冲照射时的非Fourier热传导问题，利用Laplace、Hankel变换及其逆变换，给出了一个半解析解.数值仿真表明，该半解析解能够清晰显示非Fourier热传导问题中的热波现象.

非Fourier效应；半解析解；积分变换；热弛豫时间

MSC 2010：35Q79；80A20

经典热传导问题的理论基础是Fourier扩散模型，在该模型中，热传播的速度通常被假定为无限大，但该假设在使用激光或微波进行快速加热的过程中，或材料本身有较大热弛豫时间时，都是不成立的[1-3].为描述在这些情况下的热传导问题，Cattaneo[4]和 Vernotte[5]首先将热弛豫时间引入了热传导模型，该模型被称为 Cattaneo-Vernotte (CV) 模型.CV 模型是一种双曲型模型，故热的传播也将具有类似波的特性.

研究人员已经针对CV模型，深入探讨了模型的解析解或数值解.但是，由于CV 模型控制方程的复杂性，人们很难给出其显式的解析解，故多数工作主要给出了该模型的数值解[6-8]或一维问题的解析解[9-10].尽管数值解法能在一定程度上对该问题进行模拟，但对其解析解的研究仍然是至关重要的，因为它可以被用来检验数值解的正确性，并评估数值方法的逼近性能.

针对具有较长热弛豫时间的材料，在表面受到激光辐照时的热传导问题，本文综合使用了 Laplace、Hankel 变换及其逆变换，导出了一个新的半解析解.此外，利用该解得到的数值结果也表明，热传导过程中的热波现象可被清晰显示.

1 数学模型

考虑激光束照射在一个半无限大材料表面上的情形(图1).由于激光光束具有轴对称的性质，故可用柱坐标来研究该热传导问题.令T为材料温度.由于在平行于材料表面的平面上温度分布与幅角无关，故可假定T=T(r,z,t)(r≥0,z≥0,t≥0)，其中r为极径，z为指向材料内部并垂直于材料表面的竖轴，t表示时间.本文中的物理量均使用国际单位制.在激光辐照下，材料的热响应方程为

(1)

a.材料表面温度场在空间上的分布；b.材料表面温度场最高温度随时间的变化曲线.图1 激光束照射在半无限大材料表面上的温度分布Fig.1 Thermal distribution of laser beam irradiating on the material

由于辐照深度一般是比较小的[11]，故可使用如下边界条件来近似激光光束突然照射在材料表面时的热分布

(2)

其中H(t) 为Heaviside阶跃函数，p和q为刻画激光束温度分布的参数.在材料表面，激光束产生的温度分布如图1a所示.由于激光照射的时间通常较短，故激光束的最高温度随时间t的增加快速衰减如图1b.

沿着z轴方向，由轴对称的性质可知

(3)

此外，方程的解还需满足如下的正则性条件

(4)

及初始条件

(5)

综上，激光辐照下材料内温度分布的问题即可转化为求方程(1)满足条件(2)-(5)的解.

2 半解析解

首先，对方程(1)中的变量t做Laplace变换，然后再对变量r做Hankel变换，结合条件(2)-(5)，可得

，

(6)

(7)

求解方程(6)和(7)，可得如下解析解

(8)

由于逆Hankel变换的解析形式通常不容易得到，故为能够从式(8)导出原问题的半解析解，可按式(9)交换积分次序

(9)

2.1 非Fourier热传导问题的解(即γ=ρ0c0/k0且τ0≠0)

对式(8)做逆Laplace变换可得

(10)

其中

将式(10)带入式(9)，并利用条件(2)-(5)可导出非Fourier热传导问题的半解析解

(11)

2.2 Fourier热传导问题的解(即γ=ρ0c0/k0且τ0=0)

当τ0=0时，式(8)可化为

.

对上式进行逆Laplace变换，可得

(12)

其中

.

将式(12)带入式(9)可得Fourier热传导问题的半解析解为

(13)

2.3 稳态热传导问题的解(即γ=0)

在γ=0时，方程(1)化为齐次微分方程，式(8)可化为

对上式进行逆Laplace变换，可得

(14)

其中，g3(ξ,z,t)=e-zξ-qt.将式(14)带入式(9)，可得稳态热传导问题的半解析解为

(15)

3 数值算例

由于皮肤是一种具有较大热弛豫时间的材料，故本文中使用文献[12]中给出的参数进行数值计算，即ρ0=1 000 kg/m3，c0=4 200 J/(kg·K)，k0=0.5 W/(m·K)，τ0=20 s.另外，取p=1 000及q=0.2. 图2和图3给出了在相同的初边值条件下，本文求得的非Fourier问题、经典Fourier问题及稳态热传导问题的半解析解之间的对比.

图2给出了在t=10 s时，无量纲化后的温度沿z轴(r=0)的分布曲线.由图2可以看出，一方面根据稳态热传导和经典Fourier热传导问题的定义，在相同的时间，同一深度处，经典Fourier热传导问题的解比稳态热传导问题的解略小；另一方面，由于非Fourier热传导问题中，热是以有限速度传导的，故在相同时间，同一位置处非Fourier热传导问题的解在“热波前”后时(在“热波前”左侧)比稳态和经典Fourier热传导问题解的取值都大，而在“热波前”前(在“热波前”右侧)则始终为0.热波的波前将随着时间t的增加从左向右传播(图3)，可清晰见到热波从皮肤表面向皮肤纵深传播的现象.

z/mm图2 沿z轴的温度分布，t=10 sFig.2 Temperature distribution along z-axis，t=10 s

z/mm图 3 材料内部热波前的传播，τ0=20 sFig.3 Propergation of thermal wave inside material，τ0=20 s

图4、图5、图6分别给出了t=2、8、14 s时，使用文中求得的稳态热传导问题、经典Fourier热传导问题和非Fourier热传导问题半解析解得到的材料内部温度分布的等高线图.可以看出，Fourier热传导问题与非Fourier热传导问题对应的等高线与稳态问题对应的等高线相比，相对较为扁平，同时，由图6也可看到非Fourier热传导问题的“热波前”随时间增加逐渐向材料内部移动的现象.

a.t=2 s；b.t=8 s；c.t=14 s.图4 稳态热传导问题材料内部温度场等高线Fig.4 Contour plot of steady thermal propagation problem inside material

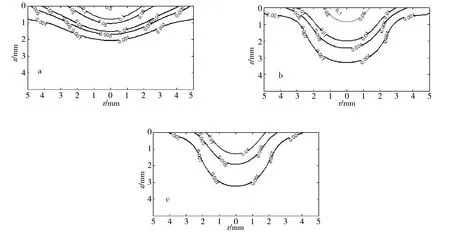
a.t=2 s；b.t=8 s；c.t=14 s.图5 Fourier热传导问题材料内部温度场等高线Fig.5 Contour plot of Fourier thermal propagation problem inside material

a.t=2 s；b.t=8 s；c.t=14 s.图6 非Fourier热传导问题材料内部温度场等高线Fig.6 Contour plot of non-Fourier thermal propagation problem inside material

4 结论

本文使用Laplace、Hankel变换及其逆变换，给出了一个对具有较长热弛豫时间的材料，在表面受到激光束突然照射时热传导问题的半解析解.数值算例表明，非Fourier热传导问题中的热波现象可在该解中清晰显示.利用实验数据，修正模型中的参数后，即可使用该半解析解预测材料内部的温度场分布.

[1] KUANGZ，LIJ，EDW ARDSONS,et al.Ultrafast laser beam shaping for material processing at imaging plane by geometric masks using a spatial light modulator[J].Opt Laser Eng，2015，70: 1-5.DOI:10.1016/j.optlaseng.2015.02.004.

[2] FARAYIBIPK，ABIOYETE，MVRRAYJ W,et al.Surface improvement of laser clad Ti-6Al-4V using plain waterjet and pulsed electron beam irradiation[J].Journal of Materials Processing Technology，2015，218: 1-11.DOI:10.1016/j.jmatprotec.2014.11.035.

[3] SHENY，YUE W，XIE A，et al.Influence of HSA on the properties of OA/OAM monolayers and the growth of calcium oxalate[J].Colloids & Surfaces A Physicochemical & Engineering Aspects，2004，234(1-3):35-41.DOI:10.1016/j.colsurfa.2003.12.004.

[4] CATTANEOC.A form of heat conduction equation which eliminates the paradox of instantaneous propagation[J].Compte Rendus，1958，247: 431-433.

[5] VERNOTTEP.Les paradoxes de la theorie continue de l'equation de la chaleur[J].Compte Rendus，1958，246: 3154-3155.

[6] ZHANGMK，CAOBY，CUOYC.Numerical studies on dispersion of thermal waves[J].International Journal of Heat and Mass Transfer，2013，67: 1072-1082.DOI:10.1016/j.ijheatmasstransfer.2013.08.102.

[7] STRHERGR，STROHERG L.Numerical thermal analysis of skin tissue using parabolic and hyperbolic approaches[J].International Communications in Heat and Mass Transfer，2014，57: 193-199.DOI:10.1016/j.icheatmasstransfer.2014.07.026.

[8] ZHANGMK，CAOBY，CUOYC.Numerical studies on damping of thermal waves[J].International Journal of Thermal Sciences，2014，84: 9-20.DOI:10.1016/j.ijthermalsci.2014.04.014.

[9] TZOUDY，GUOZY.Nonlocal behavior in thermal lagging[J].International Journal of Thermal Sciences，2010，49(7): 1133-1137.DOI:10.1016/j.ijthermalsci.2010.01.022.

[10] LAMTT.A unified solution of several heat conduction models[J].International Journal of Heat and Mass Transfer，2013，56(1-2): 653-666.DOI:10.1016/j.ijheatmasstransfer.2012.08.055.

[11] YILBASBS，KALYONM.Analytical solution for pulsed laser heating process: convective boundary condition case[J].International Journal of Heat and Mass Transfer，2002，45(7): 1571-1582.DOI:10.1016/S0017-9310(01)00239-3.

[12] JINGL，XUC，XULX.New thermal wave aspects on burn evaluation of skin subjected to instantaneous heating[J].IEEE Transactions on Biomedical Engineering，1999，46(4): 420-428.

(责任编辑：王兰英)

Semi-analytic solution of the non-Fourier thermal propagation on the surface of material irradiated by laser beam

ZHANG Lijing，SHANG Xinchun

(School of Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China)

The non-Fourier model of heat transfer as a laser pulse irritating on surface of material with large thermal relaxation time is considered.A new semi-analytic solution is derived by using Laplace，Hankel and their inverse transforms.By numerically simulating the solution，the wave form behavior of temperature can be seen clearly.

non-Fourier effect；semi-analytic solution；integral transform；thermal relaxation time

10.3969/j.issn.1000-1565.2016.05.001

2016-04-27

爆炸科学重点实验室开放基金资助项目( KFJJ12-12M)；国家自然科学基金资助项目 (10772024)

张丽静(1973—)，女，山西大同人，北京科技大学讲师，主要从事应用数学及热力耦合问题的研究. E-mail:zhanglij@ustb.edu.cn

尚新春(1958—)，男，山西朔州人，北京科技大学教授，博士生导师，主要从事热学、力学问题的研究. E-mail:shangxc@ustb.edu.cn

O39

A

1000-1565(2016)05-0449-06