浅谈小学数学中数形结合解题的重要性

丁冬青

（山西省河津市城区中心校城北小学）

浅谈小学数学中数形结合解题的重要性

丁冬青

（山西省河津市城区中心校城北小学）

在小学数学教学过程中,教师应根据小学生的认知规律，引入形象思维，注重数形结合，创设由形象思维过渡到抽象思维的中间环节，激发学生的学习兴趣，使学生真正喜欢数学并形成活泼的教学局面，从而全面促进学生思维能力的发展。

小学数学；数形结合；直观；重要性

“数无形时少直觉，形少数时难入微；数形结合百般好，隔离分家万事休。”这是数学家华罗庚先生对于数形结合的精辟论述。在小学数学教学过程中，注重数形结合，激发学生的学习兴趣，从而全面促进学生思维能力的发展。我在教学实践中根据自己的理解也做了这方面的努力，下面具体谈谈我的一些浅见。

一、以形助数，形象直观

在数学教学过程中，经常会有抽象的数学概念和复杂的数量关系，由于小学生思维的局限性，很多学生对这方面的内容理解的不是很到位，所以见到这方面的试题无从下手。在教学中，我借助图形使之形象化、直观化，把抽象的数学语言转化为直观的图形，让数学语言直观化，让学生理解起来不是那么难，变难为易，提高学生的学习积极性和思维的活跃性，通过直观的图形揭示数和形之间的内在联系，开阔学生的思维，让学生觉得简单易懂，从而爱上数学课。

例如，“真分数和假分数”的教学属于概念教学。单纯的死记硬背，灌输概念一定会是死气沉沉的课堂局面。所以，我改变教学方式，把概念化的东西直观化，渗透数形结合的思想，开启学生的数形思维。

首先，借助直观，孕伏概念。让学生自带小圆片，自己动手，感受分数，把概念直观化，让学生感受数学语言，激活学生的形象思维，目的是让学生从分数意义的角度对真分数、假分数的特点有初步的感知。其次，继续动手操作，感知概念。让学生在自制的圆片上涂色，通过分类，感受分数的不同点，再运用“形”与“数”的关系把抽象的数学概念与直观的图形结合起来，引导学生观察比较这两组分数，通过直观感受感知分数的分子与分母的大小关系，抽象出真分数和假分数的概念；使抽象思维和形象思维相结合，抓住概念的内涵，明确了真分数与假分数的不同，让学生在动手中深刻理解真分数与假分数。

又如，学生学习“圆柱和圆锥”一课时有这样一道题：一个圆锥与一个圆柱的底面积相等，已知圆锥与圆柱的体积比是，圆锥的高是3.6厘米，圆柱的高是多少厘米？初步学习的学生对“圆柱和圆锥之间变化关系”理解不是很深刻，解决问题较为困难，为突破这个难点，我把问题直观化处理，设计了下面的图表来帮助学生理解数量关系。

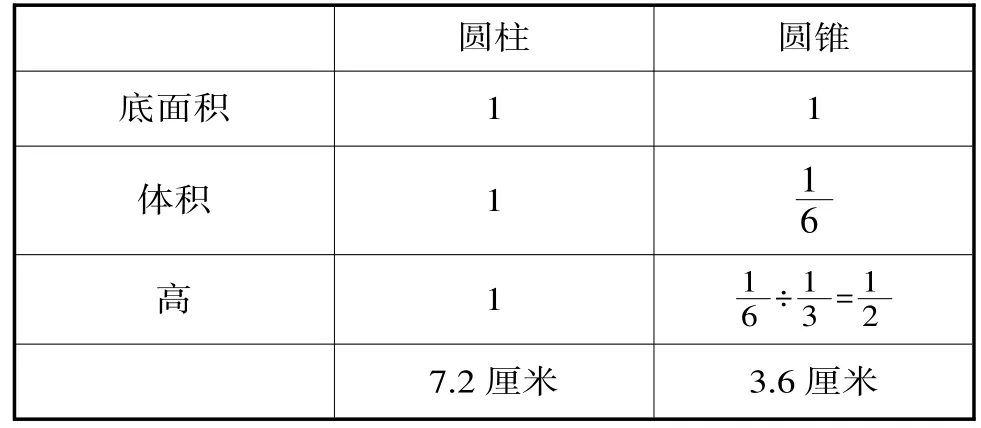
圆柱 圆锥底面积 1 1体积 1 1 6高1 7.2厘米 3.6厘米1 6 ÷1 3 =1 2

让学生根据对图表的观察、分析、联想（先分别去求高的份数的倍数关系，再去求圆柱的高）使问题一目了然。这样用“形”帮助来解决“数”的问题，避免繁杂的计算，获得出奇制胜的解法，因此，这种方法既激发了学生学习的情趣，又促进了学生思维能力的发展。学生的学习积极性也有了很大的提高。

二、以数解形，细致入微

“以数解形”就是有些图形太过于简单，直接观察却看不出蕴含着的数量关系，这时就需要给图形赋值，借助“数”的运算解决有关几何问题，用数的精确性来阐明形的某些属性和特征等。这样让学生在“见形”过程中有目的地去“思数”，在“思数”的过程中利用“数”来解释“形”，既体会到用数解形的细致入微，又提高了学生的思维能力。让学生对数形结合的思想有了进一步的理解和感悟。

例如，一个正方形边长10厘米，A、B分别是两边的中点，（如图）求阴影部分的面积？

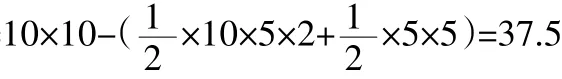
让学生学会这个解题方法后，我继续引导学生：再仔细看图，分析“中点”的条件，我们还发现更简单的解题方法。①和②的面积相等，都是正方形面积的，③是正方形面积的，阴影部分面积正好是正方形面积的，即（平方厘米）。以上通过数的运算，使形的问题得到了解决。

因此，运用数形结合思想，有利于学生分析题中数量之间的关系，让学生感受数学的魅力，从而激发学生的求知欲。

三、数形结合，彰显神奇

小学数学中虽然没有学习函数，但还是慢慢地开始渗透函数的思想，为初中数学学习打好基础。如，用直线上的点表示数；在确定位置中，用数对表示平面图形上的点，点的平移引起了数对的变化，而数对的变化又对应了不同的点。还有，在六年级下学期学习“比例”时，让学生通过描点连线来表示变化的两个量之间的关系图象，发现成正比例的两个量之间关系，画在坐标图中就是一条直线，数形在此成为一体，从而体会到图形与函数之间密不可分的关系，彰显了数形结合的神奇。培养了学生学习的兴趣，充分调动了学生思维的积极性，促进学生的思维能力向高层次发展。

总之，在小学数学教学中，数形结合的思想渗透在数学教学的每一个领域，我们要开阔学生的解题思路，让学生真正学会用数形结合的思想解决问题。

季晶.数形渗透 思维开花：浅谈小学数学教学中数形结合思想渗透策略［J］.小学教学参考，2014（8）：70.

·编辑 王团兰