弹支航空液压管路的加速度载荷响应分析

权凌霄， 李 东,2， 王鸿鑫， 曹 源

(1.燕山大学 河北省重型机械流体动力传输与控制实验室，河北 秦皇岛 066004；2. 中航工业金城南京机电液压工程研究中心，南京 210000； 3. 上海飞机设计研究院，上海 200232)



弹支航空液压管路的加速度载荷响应分析

权凌霄1， 李 东1,2， 王鸿鑫3， 曹 源1

(1.燕山大学 河北省重型机械流体动力传输与控制实验室，河北 秦皇岛 066004；2. 中航工业金城南京机电液压工程研究中心，南京 210000； 3. 上海飞机设计研究院，上海 200232)

承受加速度载荷激励的管路应力分析是飞机液压管路设计重点考虑的问题之一。基于响应谱分析方法，研究航空液压管路在加速度载荷作用下的应力响应规律。采用“梁”模型建立两端固支液压管路的动力学数学模型，求解其固有频率；建立其有限元模型进行模态分析，得到管路固有频率。通过锤击实验验证了动力学模型和有限元模型的准确性。以加速度为载荷，对弹支管路进行响应谱分析，发现最大应力出现在管路支承位置，在此基础上，改变管路承受的加速度载荷和支撑刚度，仿真结果表明最大应力值与加速度大小成线性关系，与支撑刚度成非线性关系。

弹支；管路；加速度激励；响应谱；应力

飞机电液动力控制与作动系统主要功能是进行二次能源动力传输分配与作动执行，按预定任务完成飞机飞行控制与操纵。发动机是飞机的心脏，电液动力控制与作动系统就是血管与肌肉，是飞机健壮体魄的标志[1-2]。然而，液压管路故障是飞机最常见的故障形式之一[3]。据民航总局统计，近年来，民机元件类故障中，管路失效导致的故障占到52%以上。管路的动力学性能及可靠性直接影响液压系统可靠性和使用寿命[4-6]。

由管内压力及外载荷等引起的一次应力，以及由位移载荷作用引起的二次应力[7]是否合理，是飞机管路设计的一个重要标准[8-9]。FERRS等[10]研究了环形管路在内压力作用下的应力计算方法，并对其进行了简化，为管路流固耦合计算提供了新思路。MOSHAYEDI等[11-12]研究了焊接残余应力载荷对管路应力集中造成的影响。马爱梅[13]研究了管路内介质流动造成的管路内壁不均匀作用力对弯管应力分布的影响，提高了应力计算的精度。李茂华[14]针对建立了管路的热应力有限元模型，应用ANSYS分析了压力及温度变化时，管路应力及应变的变化规律。秦叔经[15]讨论了由端点位移产生的应力计算方法，并指出位移应力具有自限性特点。

飞机飞行过程中，大多承受温度、机体变形、加速度等多种载荷的单独或共同耦合作用，这些载荷对管路应力会产生明显影响。由于在机身俯仰，受到侧向突风或离散突风，或以最大垂直力着陆角度着陆时，管路上均会承受阈值变化较大(-1 g～+5 g)的加速度载荷，严重时使管路产生明显的应力集中[16-18]，导致管路破裂。因此，研究加速度载荷对飞机液压管路应力的作用规律，具有重要意义。机翼的变形会使内部管路具有较大的应力集中，对翼尖位置的液压管路进行研究，是把握整体管路性能的基础。

本文建立了国产某型大飞机机翼翼尖一段液压直管路动力学模型和有限元模型，并分别对其求解，得到管路表面的应力云图和最大应力点。并通过锤击实验模态，验证前述模型的准确度。进而利用响应谱分析方法，研究管路受到加速度激励时的一次应力变化规律。

1 管路动力学模型及数值求解

管路振动表现为扭转振动和弯曲振动，后者为主要振动形式[19]。利用梁模型建立管路动力学模型，需做如下假设：① 管路各截面中心轴在同一平面内，且只在该平面内作弯曲振动；② 不计转动惯量和剪切变形的影响；③ 不考虑截面绕轴线的扭转。进一步，沿管路轴线方向取微元段dl，其在“y-z”平面内的受力分析如图1所示。

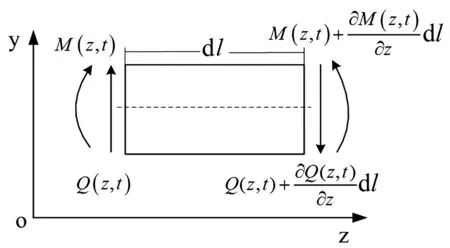
图1 管路微元段受力分析Fig.1 Stress analysis of infinitesimal pipe

图1中，Q(z，t)为剪切力，M(z，t)为弯矩，根据牛顿第二定律得到管路在y方向的运动方程为

(1)

式中:ρ为管路密度，A为管路截面积。

对微元段左侧截面列弯矩平衡方程为

(2)

忽略二次项，由式(2)可以得到剪切力与弯矩之间的关系为

(3)

根据梁的挠曲线微分方程得到弯矩表达式为

(4)

式中:E为管路的弹性模量，J为转动惯量，y(z,t)为挠度函数。

将式(3)、式(4)代入式(1)得到梁横向振动的偏微分方程为

(5)

上述方程的解对时间和空间是分离的，因此令y(z,t)=Y(z)T(t)，其中Y(z)为振型函数，T(t)为关于时间t的函数。将上式代入式(5)中，可以得到关于空间变量z的微分方程为

(6)

其中

(7)

式中:ω即为固有频率。

式(6)的通解为

Y(z)=C1sinφz+C2cosφz+C3shφz+C4chφz

(8)

式中:C1、C2、C3、C4为积分常数，由边界条件确定。对于固支管路，有如下边界条件

(9)

根据式(8)，由第一组边界条件可得到C1与C3及C2与C4的关系式

(10)

将第二组边界条件及式(10)代入式(8)中，得到关于C3及C4的方程组，将结果写成矩阵形式，得到如下方程

(11)

式(11)应满足有非零解的条件，故其系数矩阵行列式的值应为零。因此，得到特征方程为

cosφL·chφL=1

(12)

求解式(12)，可得前两个特征值分别为(φL)1=4.730，(φL)2=7.853。管路长度已知，则由式(7)可求得管路固有频率。本文基于上述计算方法，得到了长度为1 m的管路，前两阶固有频率分别为240.32 Hz、662.42 Hz，长度为2 m的管路，前两阶固有频率为60.08 Hz及165.6 Hz。

2 数值模态分析

2.1 实体建模及物性参数设置

选取C919翼尖位置的一段直管路，管路外径为38 mm，壁厚为1.5 mm，长度为1 m，管路材料牌号为不锈钢21-6-9，密度为7.76×103kg/m3，弹性模量为190 GPa，泊松比为0.27。

2.2 网格划分

在ANSYS软件中，建立所管路有限元模型。采用四面体网格进行网格划分，网格大小为4 mm，得到具有397 960个节点、198 848个单元的网格模型，如图2所示。

图2 管路网格模型Fig.2 Grid model of pipeline

本文所划分网格的平均倾斜度为0.196，根据倾斜度标准(Skewness)对其评判为优秀[20]。

2.3 网格划分

管路振动模态分析的关键是设置管路的约束。本文在后续实验中，将管路两端固支，因此，在数值模态分析时，将管路两端约束设置为固支，约束两端的全部自由度。

模态分析得到管路前2阶振型如图3所示，并得到各阶固有频率为，ω1=235.68 Hz,ω2=633.78 Hz。可以看出，前2阶振型均为平面内的弯曲振动。同样，将管路长度设置为2 m，得到对应的前2阶固有频率为ω1=59.8 Hz，ω1=163.78 Hz。

图3 两端固支管路前两阶振型Fig.3 The first two vibration modes of Clamped line

3 锤击实验模态分析

为验证理论计算及仿真计算的准确性，分别对1 m及2 m长的管路进行实验模态分析。

3.1 实验系统介绍

搭建了可拆装航空液压管路安装台架，使其能够根据管路空间构型方便地安装实验管路；基于美国NI(National Instruments)搭建了多通道数据采集系统；采用三轴压电式加速度传感器检测管路振动。

实验管路安装如图4所示，管路两端支架的刚度及安装预紧力均很大，满足管路两端固支的边界条件，可以认为管路处于固支状态。

图4 实验管路Fig.4 Experimental line

基于δ函数的脉冲响应频谱，其固有频率附近，简谐分量较大，有利于提取固有频率，因此，本文采用ICP力锤对管路施加脉冲激励。

3.2 固有频率测试

所采用的力锤带有弹性碰撞垫，可保证试验中获得理想激励脉冲信号。图5所示为力锤发出的脉冲激励，该信号在1 000 Hz频率范围内，谱线仍较为平直，满足本次实验的要求。

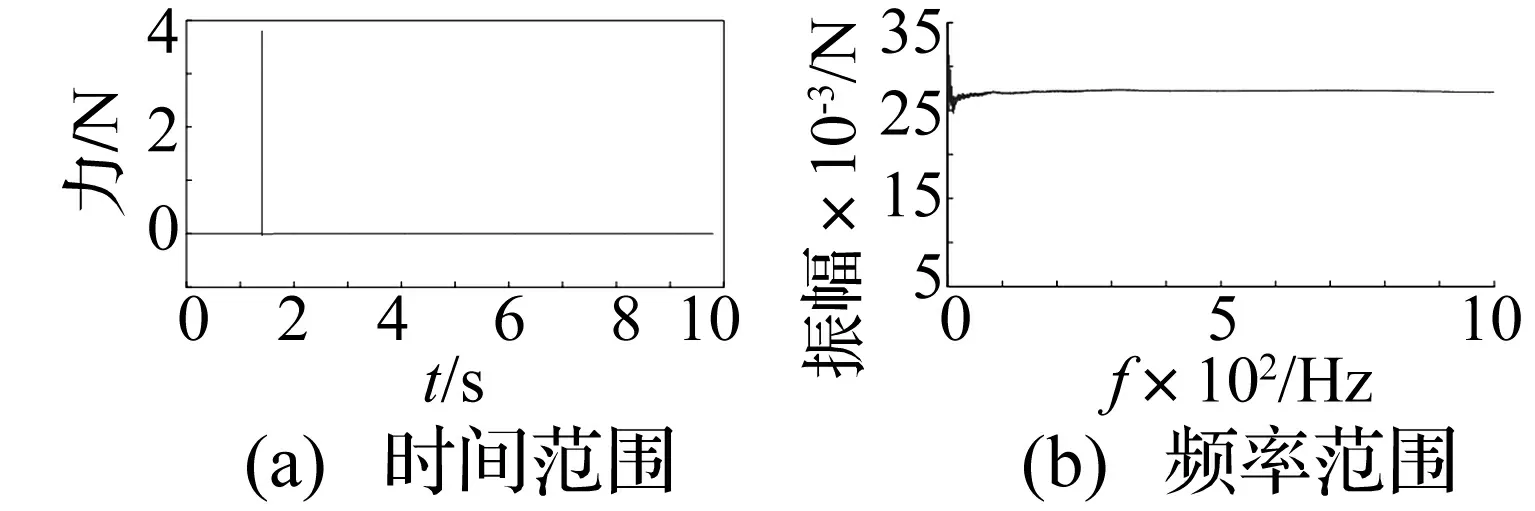
图5 力锤信号Fig.5 Hammer signal

对测得的振动信号进行小波消噪，并经过FFT变换得到其频域特性，得到管路振动频域响应如图6所示，进而得到管路固有频率。

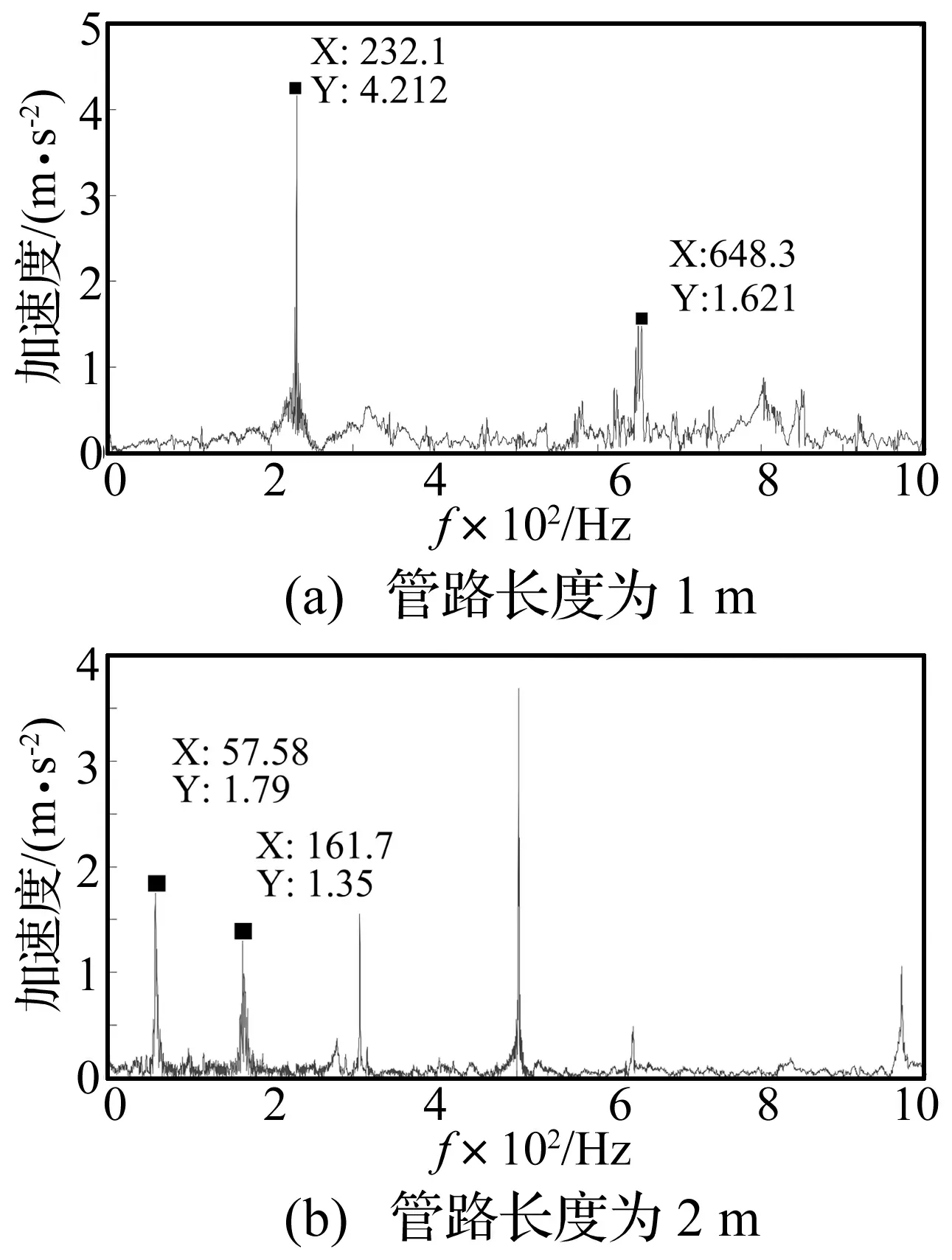
图6 管路的频域响应Fig.6 The frequency response of pipe

理论计算、模态分析及实验测得的管路固有频率如表1所示，表中频率单位为Hz，fT为理论计算结果，fS为模态分析结果，fM为实验结果，ET-E是理论计算与实验测试结果之间的相对误差，ES-E是模态分析与实验测试结果之间的相对误差。

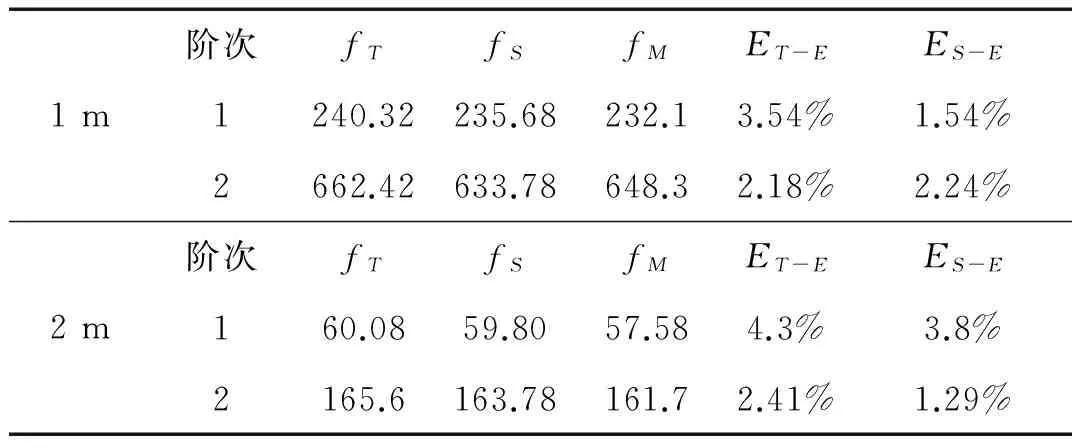
表1 管路长度为1 m及2 m时，三种研究方法的结果比较

可以看出，模态分析结果比理论计算小，这是由于ANSYS模型中，考虑了有限元之间的剪切作用和惯性矩的作用。此外，理论计算和模态分析均与实验结果存在误差。误差产生的主要原因有两个。首先，理论计算规定了假设条件，将分析对象做了理想化处理，模态分析也假设材料为线弹性材料，且忽略阻尼作用，是一种近似分析方法。此外，实际管路支架不是理想化固定支承，支承刚度不可能无穷大。但是，模态分析与实验测试的相对误差最大为3.8%，表明模态分析的研究方法精度很高。

4 弹支管路响应谱分析

基于上述管路有限元模型，研究特定约束条件下，管路承受加速度激励时，管路表面应力分布规律及最大应力与加速度幅值的关系。飞机液压管路都采用弹性支撑，管路在受到外界激励作用时，主要表现为横向振动[19]，因此，该部分研究以横向直线约束为主要边界条件。

4.1 约束设置

如图7所示，在管路两端设置位移约束，设置z方向位移为0，以限制轴向运动；设置x及y方向的约束为径向弹簧，刚度分别为kx、ky，以提供径向弹支约束。

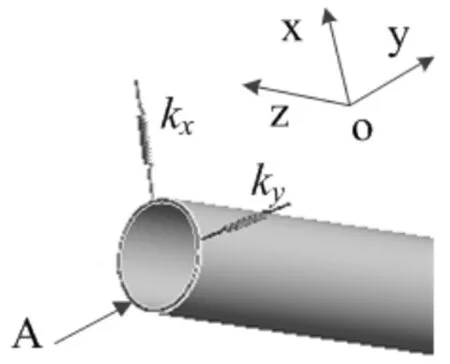
图7 管路一端约束设置Fig.7 Constraint set of one end of the pipe

4.2 加速度响应谱分析

民用飞机机翼在稳定俯仰时，会承受频率为100 Hz，幅值为-1 g～2.5 g的加速度激励，考虑-1 g加速度与1 g加速度在方向上的对称性，计算时取加速度方向为x方向，范围为0.5 g～3 g。得到管路在2.5 g加速度时的应力云图如图8所示。可以看出，加速度载荷下，最大应力出现在管路支撑处。

图8 2.5 g加速度激励下的应力响应Fig.8 Stress response under acceleration excitation

下面分析加速度大小与最大应力变化间的规律。将加速度幅值在0.5 g～3 g之间取连续变化的几个量，以0.5 g为步长，得到加速度幅值变化时，最大应力的变化曲线如图9所示。

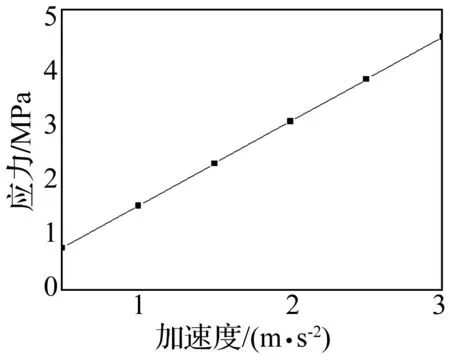
图9 应力随加速度变化Fig.9 Stress change with acceleration

可以看出，由于加速度载荷与管路质量成线性关系，在管路上将会产生线性载荷力，因此，最大应力与加速度大小成线性关系，斜率为1.51，加速度越大，管路支撑处受到的应力越大。因此，在管路设计时，应以最大加速度作为载荷进行计算。

将支撑刚度取为1×105N/m-1×109N/m，得到当支撑刚度对最大应力的影响如图10所示。

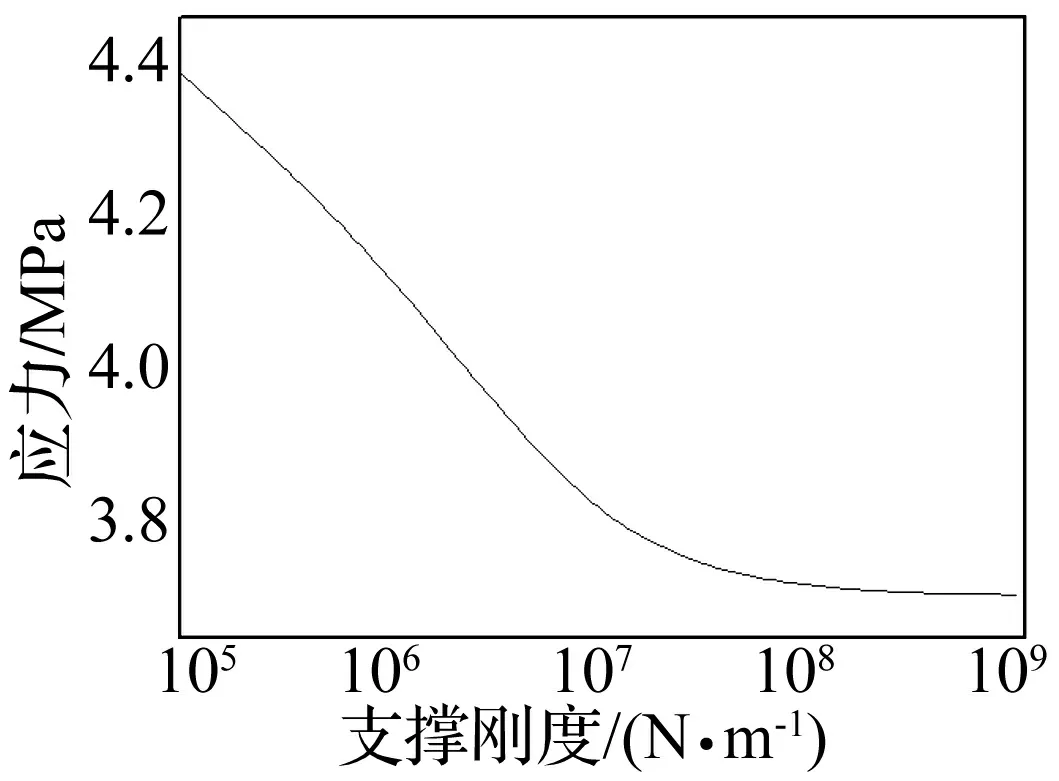
图10 支撑刚度对最大应力的影响Fig.10The influence of stiffness on the maximum stress

可以看出，随着支撑刚度增大，最大应力降低。当支撑刚度小于某特定值时(0.9×107N/m)，支撑刚度与最大应力近似为线性关系；而当刚度大于该值以后，二者为非线性关系。当支撑刚度大于另一特定值时(1×108N/m)，增大支撑刚度，最大应力值基本不变。这是由于应力是材料内部抵抗变形而产生的反作用力[21]，当刚度较低时，外界激励会产生较大的变形，从而产生较大的应力，而当支撑刚度接近固支时，管路在相同激励下产生的变形差距不大，因此应力基本不变。

5 结 论

本文在正确的有限元模型基础上，对航空液压管路进行响应谱分析，得到如下结论：

(1) 管路在受到加速度载荷激励时，支撑处应力最大。理想状态下，该应力值与加速度大小完全成线性关系，在管路设计时，应按照最大加速度进行校核。

(2) 管路在加速度激励下的最大应力与支撑刚度为非线性关系，支撑刚度越大，最大应力越小。在弹支状态下，当支撑刚度小于某一值(1×108N/m)时，最大应力与支撑刚度成反比，而大于该值时，应力变化不明显。

[1] 白欢欢．基于变刚度弹性支承的液压管路流固耦合振动的数值分析[D]．秦皇岛：燕山大学，2014．

[2] DELGADO J N, MARTINS N M C, COVAS D I C. Uncertainties in hydraulic transient modelling in raising pipe systems: laboratory case studies[J]. Procedia Engineering, 2014, 70: 487-496.

[3] KHEIRI M, PAIDOUSSIS M P, COSTA G, et al. Dynamics of a pipe conveying fluid flexibly restrained at the ends[J]. Journal of Fluids and Structures, 2014, 49: 360-385.

[4] 刘元朋, 陈良骥, 李明, 等. 航空发动机管路测量数据分割方法[J]. 航空学报, 2008, 29(2): 285-291. LIU Yuanpeng, CHEN Liangji, LI Ming, et al. Segmentation method for point cloud of aeroengine pipelines[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(2): 285-291.

[5] MITTAL R, SINGH P K, PUKAZHENDI D M, et al. Effect of vibration loading on the fatigue life of part-through notched pipe[J]. International Journal of Pressure Vessels and Piping, 2011, 88: 415-422.

[6] SIERRA-ESPINOSA F Z, GARCIA J C. Vibration failure in admission pipe of a steam turbine due to flow instability[J]. Engineering Failure Analysis, 2013, 27: 30-40.

[7] 许文欣,张强.化工设计中的管道应力分析[J].辽宁化工, 2003, 32(3): 117-119. XU Wenxin, ZHANG Qiang. Pipe stress analysis in chemical technology process design[J]. Liaoning Chemical Industry, 2003, 32(3): 117-119.

[8] MAEKAWA A, TAKAHASHI T, TSUJI T. Experimental validation of non-contacting measurement method using LED-optical displacement sensors for vibration stress of small-bore piping[J]. Measurement, 2015, 71: 1-10.

[9] JI Jian, ZHANG Chunshun, KODIKARA J, et al. Prediction of stress concentration factor of corrosion pits on buried pipes by least squares support vector machine[J]. Engineering Failure Analysis, 2015, 55: 131-138.

[10] FERRAS D, COVAS D C, SCHLEISS A J. Stress-strain analysis of atoric pipe for inner pressur loads[J]. Journal of Fluids and Structures, 2014, 51: 68-84.

[11] MOSHAYEDI H, SATTARI-FAR I. The effect of welding residual stresses on brittle fracture in an internal surface cracked pipe[J]. International Journal of Pressure Vessels and Piping, 2015, 126-127: 29-36.

[12] MOSHAYEDI H, SATTARI-FAR I. Interaction of welding residual stresses and warm pre-stressing on brittle fracture of a pipe containing an internal semi-elliptical crack[J]. Engineering Failure Analysis, 2015, 52: 116-128.

[13] 马爱梅,鹿晓阳,陈红艳.基于流体力学的弯管应力有限元分析[J].机械设计,2006, 23(3): 50-52. MA Aimei, LU Xiaoyang, CHEN Hongyan. Finite element analysis on stresses of bended pipe based on fluid dynamics[J]. Journal of Machine Design, 2006, 23(3): 50-52.

[14] 李茂华,石磊彬,钟威,等. 内外压热应力影响下西气东输二线长输管道变形的有限元分析[J].天然气工业, 2013, 33(8): 119-124. LI Maohua, SHI Leibin, ZHONG Wei, et al. The finite element analysis and calculation of pipeline stress and strain under the effect of heat stress and internal or external pressure in the West-to-East China Gas Pipeline П[J]. Natural Gas Industry, 2013, 33(8): 119-124.

[15] 秦叔经. 位移应力及其强度条件[J].化工设备与管道, 2004, 41(5): 23-27. QIN Shujing. Displacement stress and strength condition[J]. Process Equipment & Piping, 2004, 41(5): 23-27.

[16] XU Y Z, NIGEL JOHNSTON D, JIAO Z X，et al. Frequency modelling and solution of fluid-structure interaction in complex pipelines[J]． Journal of Sound and Vibration，2014，333：2800-2822.

[17] BAKRE A S V, JANGID R S, REDDY G R. Response of piping system on friction support to bi-directional excitation[J]. Nuclear Engineering and Design, 2007, 237: 124-126.

[18] OUYANG Xiaoping, GAO Feng, YANG Huayong. Modal analysis of the aircraft hydraulic-system pipeline[J]. Journal of Aircraft, 2012, 49(4): 1168-1174.

[19] 李艳华, 柳贡民, 马俊. 考虑流固耦合的典型管段结构振动特性分析[J]. 振动与冲击, 2010, 29(6): 50-53. LI Yanhua, LIU Gongmin, MA Jun. Research on fluid-structure interaction in fluid-filled pipes[J]. Journal of Vibration and Shock, 2010，29(6)：50-53.

[20] 浦广益. ANSYS Workbench基础教程与实例详解[M].北京: 中国水利水电出版社, 2013.

[21] 白象忠. 材料力学[M]．北京：科学出版社，2008．

Acceleration load response analysis for elastically supported aviation hydraulic pipe-lines

QUAN Lingxiao1, LI Dong1,2, WANG Hongxin3, CAO Yuan1

(1. Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control, YanshanUniversity, Qinhuangdao 066004, China；2. Nanjing Engineering Institute of Aircraft system Jincheng AVIC, Nanjing 210000, China;3. Shanghai Aicraft Design And Research Institute，Shanghai 200232, China)

Stress analysis under acceleration load excitation is one of the key problems in the design of aviation hydraulic pipelines. Based on the response spectral analysis method, the stress response law of aviation hydraulic pipelines under the action of acceleration load was studied. The dynamic model of a two-end-fixed hydraulic pipeline was established by using a “beam” model, and its natural frequencies were solved. Then its finite element model was established to do the modal analysis and obtain its natural frequencies. The correctness of the dynamic model and the finite element model was verified with hammer tests. The response spectral analysis of the corresponding elastically supported pipeline was performed under the acceleration load. The results showed that the maximum stress appeares at the support position of the pipeline. Moreover, the acceleration load and support stiffness were changed, the simulation results showed that the relationship between the maximum stress and the acceleration load is linear, and the relationship between the maximum stress and support stiffness is nonlinear.

elastic support; pipeline; acceleration excitation; response spectrum; stress

国家重点基础研究发展计划(973计划(2014CB046405)；国家自然科学基金(51375423)；流体动力与机电系统国家重点实验室开放基金(GZKF-201309)

2015-09-16 修改稿收到日期：2016-02-27

权凌霄 男，博士，副教授，1977年2月生

TH137;V228

A

10.13465/j.cnki.jvs.2016.21.033