呼吸性椭圆裂纹转子弯曲刚度模型

刘 政， 王建军

(北京航空航天大学 能源与动力工程学院，北京 100191)



呼吸性椭圆裂纹转子弯曲刚度模型

刘 政， 王建军

(北京航空航天大学 能源与动力工程学院，北京 100191)

通常转子轴上的疲劳裂纹为椭圆形尖端，而国内外现有文献大多关注直裂纹转子，很少对椭圆裂纹呼吸行为建立模型。提出了新的圆柱轴椭圆裂纹呼吸模型，修正中性轴位置确定裂纹张开面积，并基于裂纹应变能计算出椭圆裂纹附加柔性系数，建立了该类裂纹转子弯曲刚度模型。进一步，与文献和有限元结果进行对比，裂纹呼吸规律完全符合，裂纹附加柔度、转子无量纲挠度满足计算要求，验证了该模型有效可行。

裂纹转子；椭圆裂纹；呼吸性；弯曲刚度

航空发动机等旋转机械转子系统的转轴处于弯曲、拉伸、剪切交变载荷复杂作用下，若材料有微小缺陷，或长期高负荷工作，就可能萌生裂纹，进而扩展成疲劳裂纹。出现裂纹后，转子系统的动力响应和稳定性发生变化，结构强度也偏离设计状态。如果裂纹不被及时发现，最终导致转子失稳断裂，造成灾难性后果。因此，近年来裂纹转子受到学术界和工程界高度重视。

现有文献对直裂纹转子动力特性研究很多。突出的有，DIMAROGONAS[1]首先基于应变能提出开裂纹附加柔性系数，研究了带有张开的直裂纹转子轴向与弯曲耦合振动。JUN[2]考虑应力强度因子为零划分裂纹张开、闭合边界，研究了呼吸性直裂纹转子的稳态振动。DARPE等[3-4]进一步研究了直裂纹转子系统的瞬态振动和非线性动力学特性。

然而，实际裂纹尖端通常是弧形的，(半)椭圆形尖端裂纹是较接近实况的一种弧形裂纹模型。近年来，国内外学者开始对椭圆裂纹转轴刚度进行深入的研究。RUBIO[5]研究了完全张开裂纹的附加柔度和简支、悬臂圆柱裂纹梁的静挠度，并基于有限元法和实验进行了验证。HAN[6]进一步给出了椭圆裂纹圆轴受拉伸、弯曲作用的裂纹附加柔度。

裂纹呼吸是指在转轴旋转过程中，裂纹连续周期交替张开、闭合。这类情况接近真实转子运转的环境。在弧形裂纹呼吸机制研究方面，目前学者们多采用有限元法。KULESZA[7]采用刚性有限元(rigid finite element method)数值方法，模拟圆柱轴上裂纹的呼吸和扩展过程。ABELLA[8]基于人工神经网络(artificial neural networks)计算了偏心轴在旋转弯矩作用下的直裂纹应力强度因子，分析了偏心转轴上直裂纹的呼吸机制及其对裂纹扩展的影响。RUBIO[9]采用带椭圆裂纹转轴有限元模型，研究了椭圆裂纹张开的面积、质量偏心角、裂纹几何尺寸等变化关系。结果表明，裂纹在呼吸过程中，张开范围要大于闭合范围。

理论上的椭圆裂纹呼吸模型方面尚未有较多的关注。HAN[10]考虑裂纹呼吸性，建立了转轴弯曲振动方程，研究了椭圆裂纹转轴参数稳定性问题。该文献实际上只给出转轴弯曲方向的裂纹附加柔度，而未考虑裂纹的交叉柔度以及另一垂直方向的转轴刚度。当椭圆裂纹较大时，交叉刚度不能忽略；当转子发生瞬态振动时，垂直弯曲方向还有惯性力的作用。

鉴于以上原因，本文基于已有文献研究结果，提出圆柱轴上带有椭圆尖端的裂纹呼吸模型，并与文献和有限元结果进行对比验证模型有效可行，进一步根据Dimarogonas方法计算出椭圆裂纹附加柔性系数，建立椭圆裂纹转子弯曲刚度模型。

1 呼吸性椭圆裂纹转子刚度模型

如图1所示，本文建立椭圆裂纹转子刚度模型的主要思想为：① 在裂纹张开、不完整的圆柱轴含裂纹横截面上不考虑应力集中，根据截面静矩平衡计算中性轴位置；② 考虑到裂纹尖端应力集中，引入修正参数，修正中性轴到涡动坐标系Y′ 轴的代数距离，从而以修正后的中性轴确定裂纹张开与闭合分界；③ 在裂纹张开面积上对椭圆裂纹应力强度因子进行积分获得Griffith应变能；④ 根据Castigliano定理将应变能对集中力求两阶偏导，得到由裂纹引起的附加柔性系数，再叠加上无裂纹圆柱轴的柔度，求出带椭圆尖端裂纹转子系统的刚度。以下为呼吸性椭圆裂纹转子刚度模型的具体实现过程。

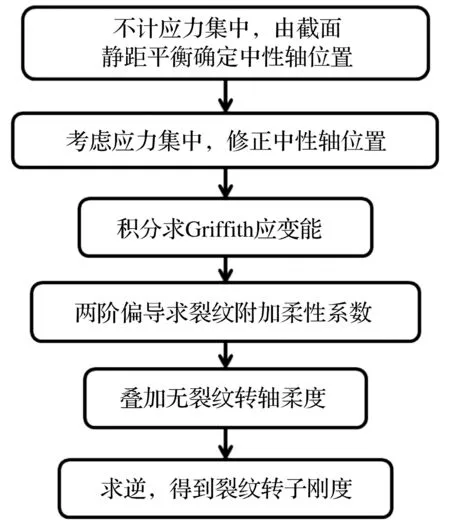
图1 椭圆裂纹转子刚度建模思路Fig.1 Procedure of stiffness modeling of a breathing elliptical cracked rotor

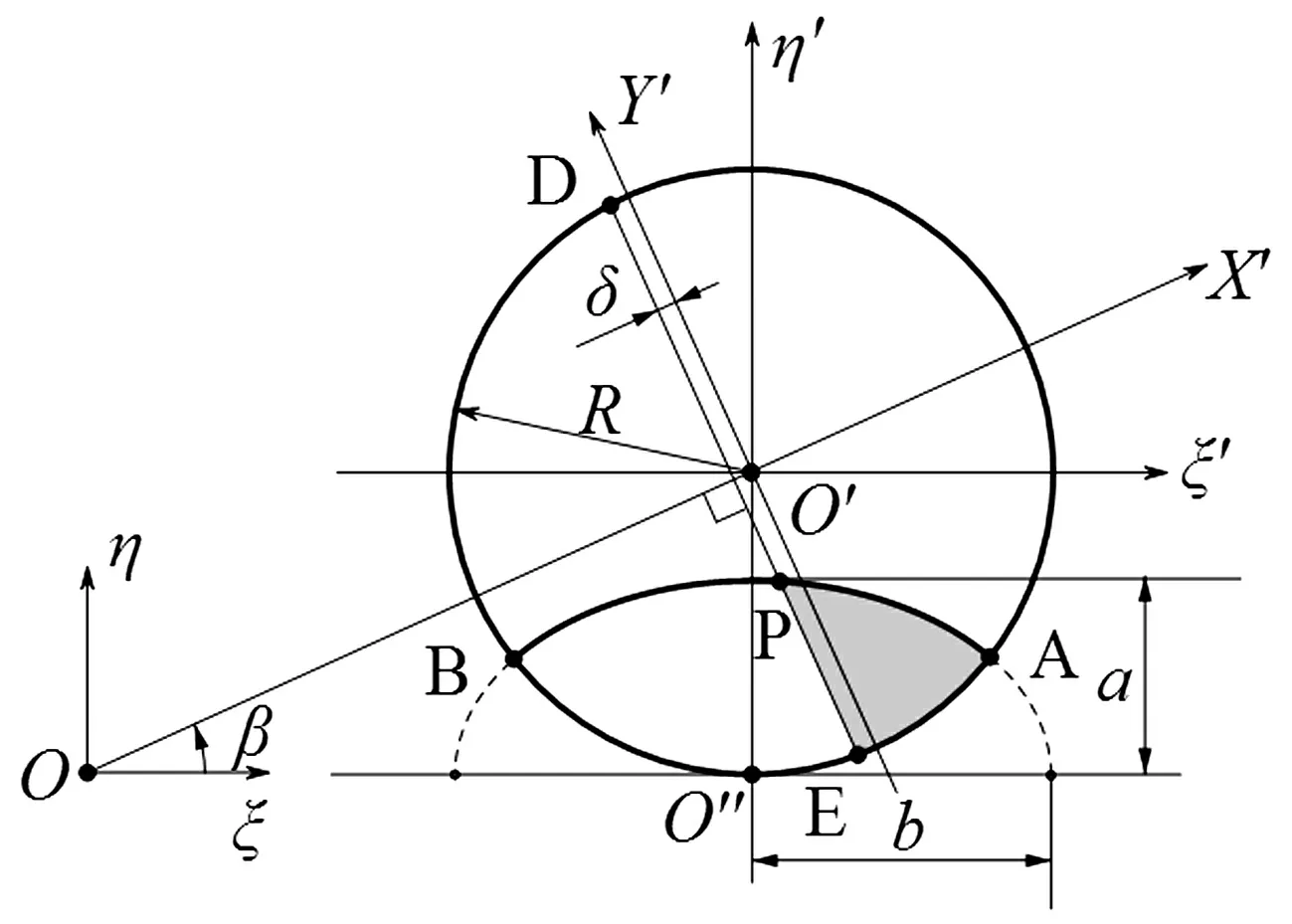
图2 椭圆尖端裂纹轴截面几何示意图Fig.2 Geometric sketch of cross profile ofelliptical cracked shaft

Oξη为自转坐标系，OX′Y′为涡动坐标系，O′ξ′η′为裂纹几何坐标系，a,b分别为椭圆裂纹半轴长，其余符号如文中所述

将尺寸对圆半径R归一化后，单位圆O′方程：

ξ′2+η′2=1

(1)

描述弧形裂纹尖端的椭圆O″方程：

(2)

描述中性轴的直线DE方程：

ξ′cosβ+η′sinβ-δ=0

(3)

此时，δ为不考虑应力集中的中性轴DE与涡动坐标系O′X′Y′轴Y′的代数距离，β为涡动坐标系O′X′Y′与旋转坐标系Oξη的转角差(涡转差角，whirl rotation angle difference)，即截面形心O′在旋转坐标系中的相位角

(4)

裂纹张开区域APEA(图2中阴影部分)表示为

(5)

裂纹Griffith应变能表示为

(6)

即在这裂纹张开面积上积分。根据材料力学理论，截面应力平衡等价于截面上未张开各点到中性轴的静矩为零，有

∬D(ξ′cosβ+η′sinβ-δ)dξ′dη′=0

(7)

其中D表示圆截面内除裂纹张开面积APEA外的区域，因此，

πδ+∬Ac(ξ′cosβ+η′sinβ-δ)dξ′dη′=0

(8)

求解方程(8)得δ=δ*。

考虑裂纹尖端应力集中效应，引入修正参数ε，令

δ=(1+ε)δ*

(9)

代入式(5)中重新描述裂纹张开面积。令w=ξ′，h=1+η′，则dAc=dhdw。

根据文献[2]，椭圆裂纹尖端P点的应力强度因子可表达为

KI=KI,ξ+KI,η

(10)

KI,ξ(a/b,a/R,w/w0)=

(11)

KI,η(a/b,a/R,w/w0)=

(12)

式中:FI,ξ采用文献[11]的数据拟合，FI,η采用文献[12]的研究结果。这里，

(13)

(14)

W=πR3/4

(15)

令椭圆裂纹参数短、长半轴比μ=a/b，相对深度α=a/R，点P在w方向相对位置χ(a)=w(a)/w0(a)。在裂纹局部坐标系中:

w0(a)=acosθ0(α)/μ

(16)

θ0(α)=

(17)

根据Castigliano定理，裂纹引起的附加柔性系数为

(18)

(19)

(20)

椭圆裂纹转子系统的总柔度由无裂纹转子柔度叠加上裂纹附加柔度，因此

(21)

当质量点位于轴正中央时，k为无裂纹轴中点处刚度，k=48EI/l3，惯性矩I=πR4/4，则转子的刚度比

(22)

(23)

(24)

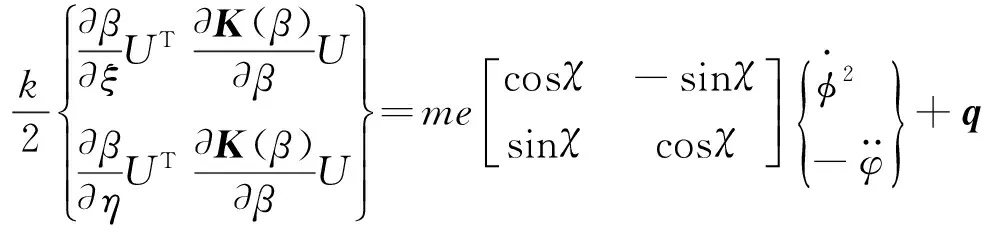
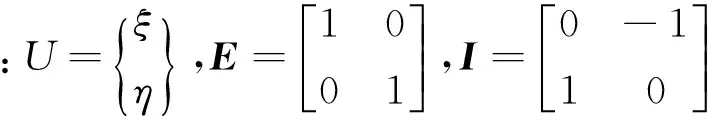
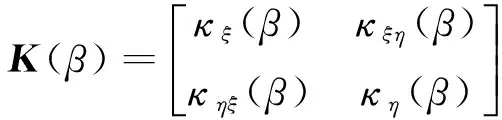
2 椭圆裂纹呼吸模型验证

为验证第1节提出的椭圆裂纹呼吸模型有效可行，本节首先与现有文献的研究进行对比，然后与椭圆裂纹圆柱轴的有限元模型计算结果进行对比。

新生儿疾病筛查是早期发现某些先天性、遗传性疾病的有效方法，随着筛查技术的不断进步，串联质谱技术［1］也得到了广泛的应用。2000年10月台州市正式开展了新生儿遗传代谢性疾病筛查，仅限于对先天性甲状腺功能减低症（congenital hypothyroidism，CH）和 苯 丙 酮 尿 症 （phenylketonuria，PKU）进行筛查。2009年10月在原筛查病种的基础上又开展了采用串联质谱技术对多种遗传代谢病筛查的工作。为了解本市新生儿遗传代谢疾病筛查现状，笔者特对2000年10月－2012年9月筛查情况进行了回顾性分析，现将结果报道如下。

本文取表征应力集中的修正参数ε=-0.4。图3为椭圆裂纹几何参数μ=0.5的中性轴与涡动轴代数距离δ随涡转差角β的变化曲线，其中依曲线μ=0.5，α=0.6画出椭圆裂纹呼吸示意图，如图4所示。

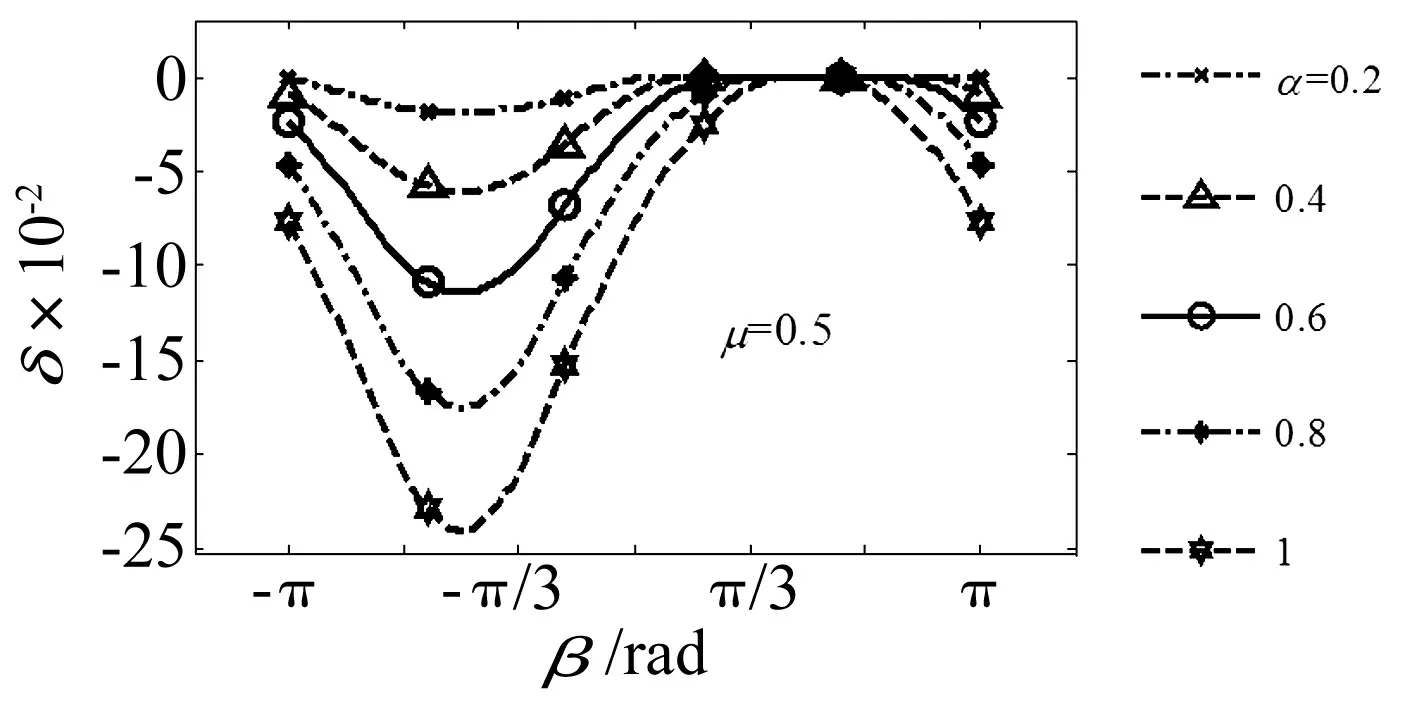
图3 修正后的中性轴位置变化曲线Fig.3 Position curves of neutral axis modified

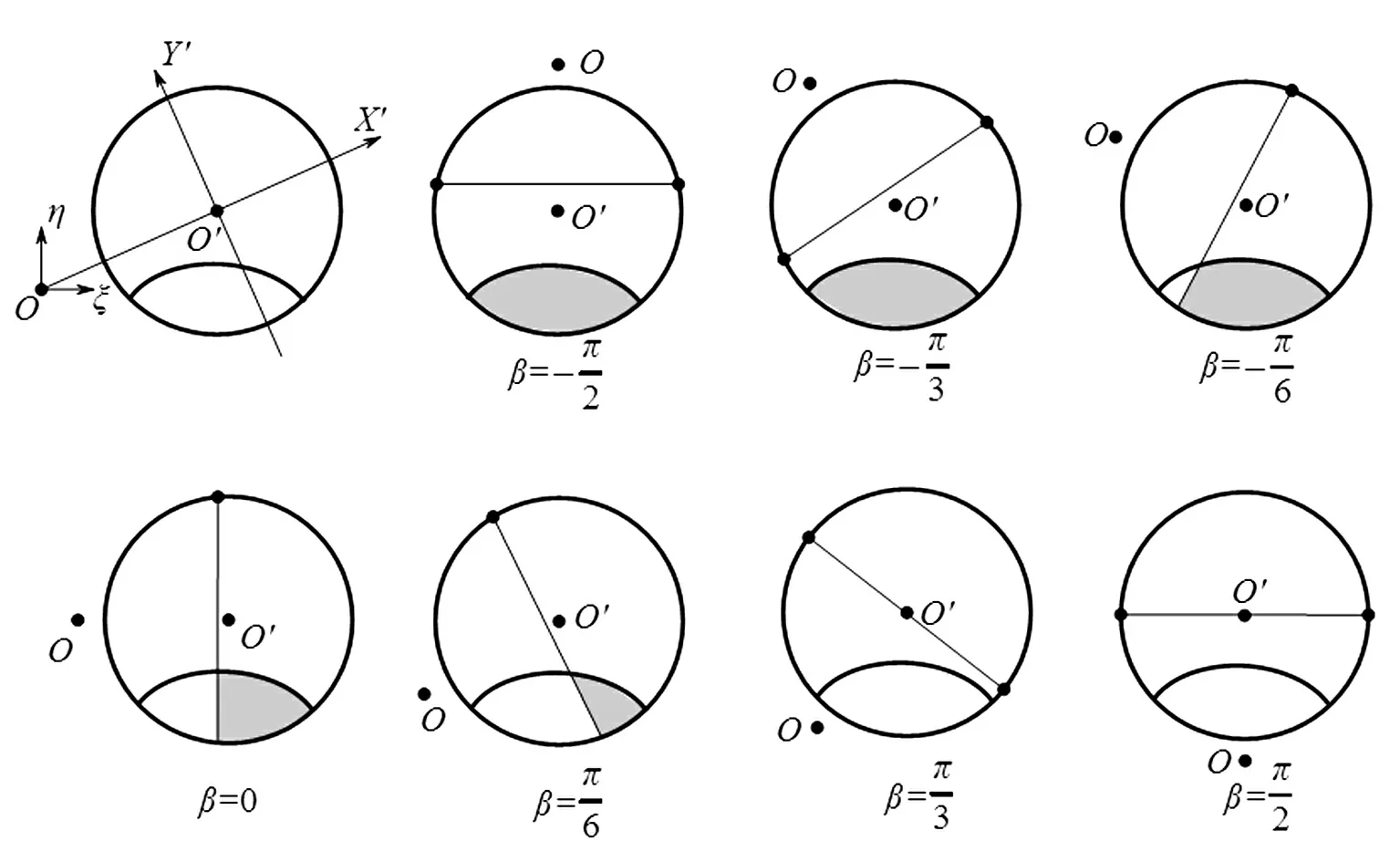
图4 本文模型裂纹呼吸行为(阴影部分表示裂纹张开区域)Fig.4 Breathing behavior of elliptical crack proposed (gray parts denote open area of crack)

对比文献[9]关于裂纹呼吸机制的研究(图11 balanced)，文献计算的裂纹张开与闭合边界为弧形，本文模型为直线。但是，裂纹呼吸的过程和基本规律完全相同。主要有：

(1) 裂纹随涡转差角变化而交替张开、闭合，存在半开半闭的过渡区；

(2) 在任意涡转差角下，裂纹更倾于张开的趋势；

(3) 在整个周期来看，完全张开范围明显比完全闭合范围大，且裂纹越深越明显；

(4) 在一个周期内，裂纹完全张开、闭合各一次，且呼吸状态关于β=±π/2(以本文模型)轴对称。

进一步，本文与文献[10]计算结果进行对比。文献[10]实质上计算的是涡动坐标系X′方向上的裂纹附加柔度。按文献[10]的无量纲比例，根据第1节计算呼吸性椭圆裂纹在涡动系X′向的附加柔度，并与文献[10]提出的椭圆裂纹附加柔度比较，如图5所示。可见，两曲线在整个周期内大致重合，但由于考虑了椭圆裂纹的交叉柔度，当裂纹接近完全闭合时，本文模型变化得更快。

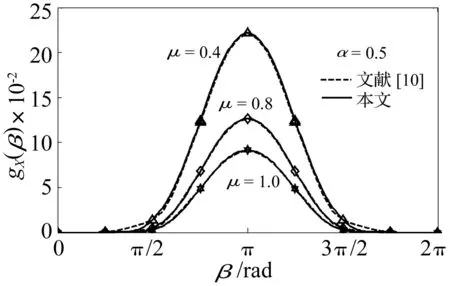
图5 本文与文献[10]计算的裂纹附加柔性系数Fig.5 Cracked additional flexibility coefficients calculated by Han and now proposed

下面基于ANSYS实体有限元模型计算裂纹呼吸表现，验证本文的理论模型。

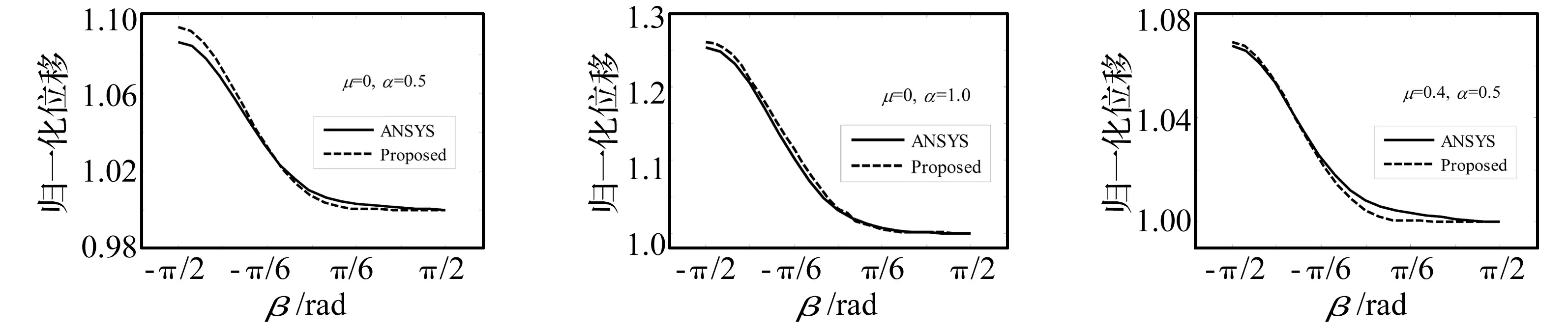
建立长l=200 mm，半径R=10 mm，正中央带有椭圆裂纹圆柱轴实体有限元模型，如图6所示。两端简支，在距离右端1/4轴长处截面中心点处加载横向集中力载荷Q。此时，裂纹局部弯矩M=(Ql)/8，Q对轴中央中心点无裂纹刚度k=(16/11)*(48EI/l3)，如图7所示。图8给出了有限元模型计算的裂纹呼吸过程。分别采用有限元模型和本文提出的理论模型，计算不同方向载荷Q作用下的中央裂纹处截面中心点的位移，并除以同载荷无裂纹轴的挠度归一化，得到椭圆裂纹轴的无量纲挠度，对比两者随涡转差角的变化曲线，如图9所示。

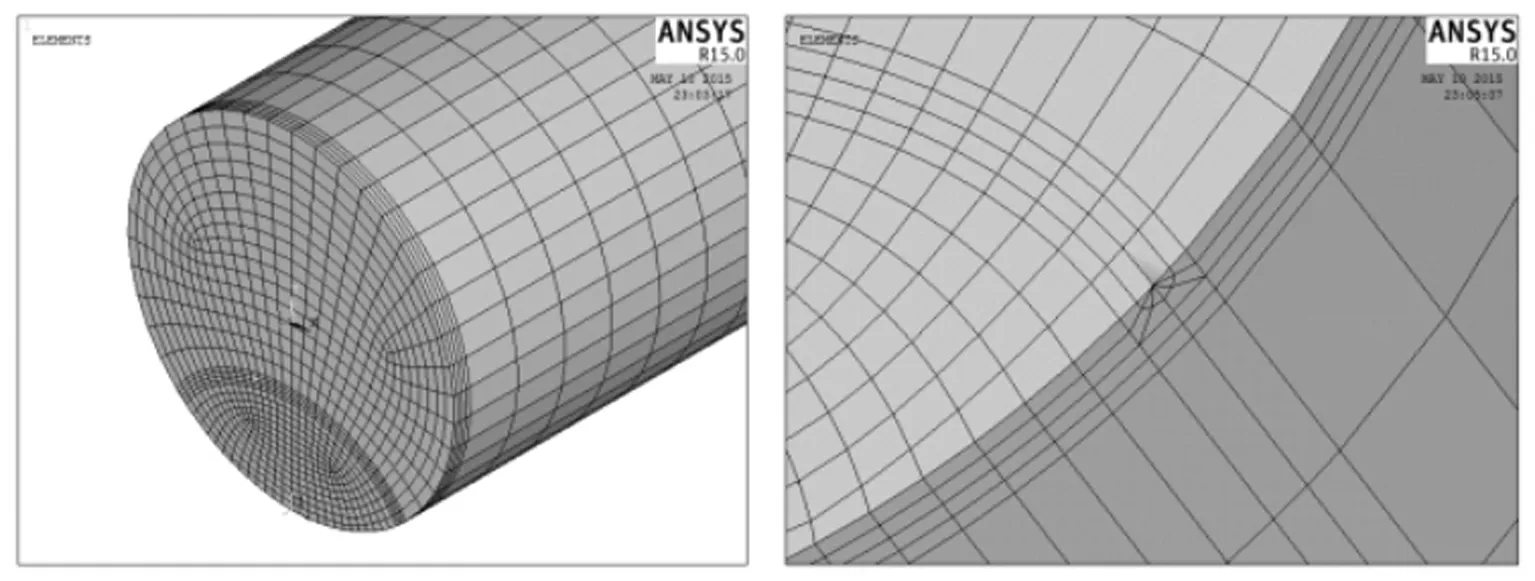
图6 椭圆裂纹圆轴有限元模型及裂纹局部放大图Fig.6 FE model of elliptical cracked shaft and partial enlarged crack detail

由图8可见，实体有限元模型的椭圆裂纹在不同载荷作用下表现出了呼吸行为，裂纹张开范围明显大于闭合范围，说明裂纹在呼吸过程中总是倾向于张开；图9表示的本文模型与有限元模型计算结果走势一致，裂纹张开与闭合点吻合，无量纲挠度值大范围相同。需要说明的是，选取合适的修正参数ε值即可调节本文模型计算精度。

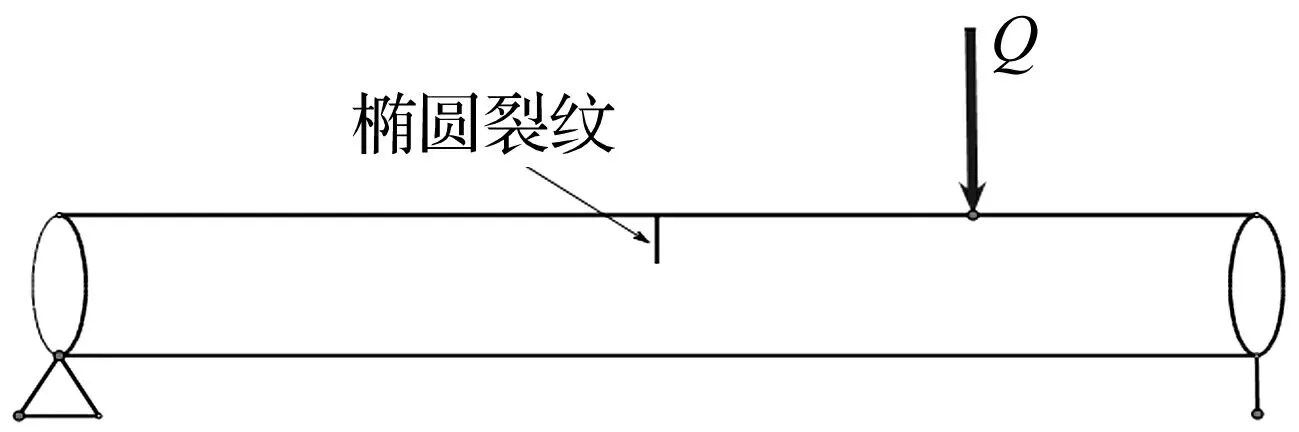
图7 有限元验证的载荷结构Fig.7 Load structure of FE model used for validation

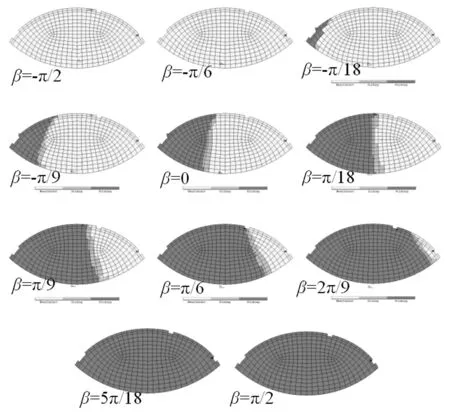
图8 有限元模型椭圆裂纹圆柱轴的裂纹呼吸行为(注：这里β为Q与ξ轴的夹角，黑色表示张开，白色表示闭合)Fig.8 Breathing behavior of FE elliptical crack model (Note: β denotes angle between Q and axis ξ, and black area stands for open part, white for close)

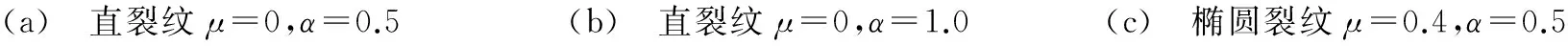
(a) 直裂纹μ=0,α=0.5(b) 直裂纹μ=0,α=1.0(c) 椭圆裂纹μ=0.4,α=0.5

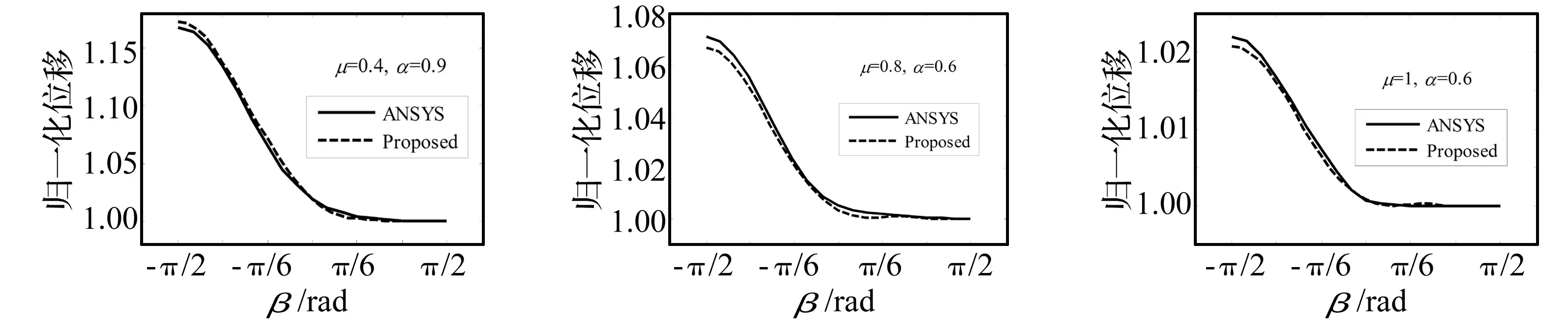
(d) 椭圆裂纹μ=0.4,α=0.9(e) 椭圆裂纹μ=0.8,α=0.6(f) 椭圆裂纹μ=1.0,α=0.6图9 本文与ANSYS计算的裂纹圆轴弯曲挠度变化曲线Fig.9BendingdeflectioncurvesofcrackedshaftcalculatedbypaperandANSYS

3 结 论

本文针对圆轴上椭圆裂纹呼吸特性，考虑了裂纹尖端应力集中效应，修正中性轴位置来建立裂纹呼吸模型；基于Dimagaranas计算裂纹附加柔度的思想，在裂纹张开面积上对应力强度因子积分得到裂纹释放的应变能，再对集中力两阶偏导获得裂纹附加柔性系数，叠加无裂纹转轴柔度得到椭圆裂纹转子受力弯曲的刚度模型。

为了检验本文模型的有效性，首先与参考文献进行对比，结果表明裂纹呼吸规律相同，考虑了交叉柔度后裂纹附加柔性系数在裂纹即将闭合时变化快于文献值；然后基于ANSYS建立了椭圆裂纹转轴的实体有限元模型，加载不同方向载荷计算出圆轴中央的无量纲挠度，同时采用本文模型计算同载荷的无量纲挠度，两者走势一致，结果吻合。验证了本文提出的裂纹呼吸模型和椭圆裂纹转子弯曲刚度模型有效可行。

[1] PAPADOPOULOS C A, DIMAROGONAS A D. Coupled longitudinal and bending vibrations of a rotating shaft with an open crack [J]. Journal of Sound and Vibration, 1987,117(1):81-93.

[2] JUN O S, EUN H J. Modeling and vibration analysis of a simple rotor with a breathing crack [J]. Journal of Sound and Vibration, 1992,155(2):173-290.

[3] DARPE A K, GUPTA K, CHAWLA A. Transient response and breathing behavior of a cracked Jeffcott rotor [J]. Journal of Sound and Vibration, 2004,272:207-243.

[4] PATEL T H, DARPE A K. Influence of crack breathing model on nonlinear dynamics of a cracked rotor [J]. Journal of Sound and Vibration, 2008,311:953-972.

[5] RUBIO L, ABELLA B M, LOAIZA G. Static behavior of a shaft with an elliptical crack [J]. Mechanical Systems and Signal Processing, 2011,25:1674-1686.

[6] HAN Q, CHU F. Local flexibility of an elliptical cracked shaft under bending and tension [J]. Mechanical Systems and Signal Processing, 2011,25:3198-3203.

[7] KULESZA Z, SAWICKO J T. New finite element modeling approach of a propagating shaft crack [J]. Journal of Applied Mechanics, 2013,80:011025-1-17.

[8] ABELLA B M, RUBIO L, RUBIO P. Stress intensity factor estimation for unbalanced rotating cracked shafts by artificial neural networks [J]. Fatigue & Fracture of Engineering Material & Structure, 2014,00:1-16.

[9] RUBIO L, ABELLA B M, RUBIO P, et al. Quasi-static numerical study of the breathing mechanism of an elliptical crack in unbalanced rotating shaft [J]. Latin American Journal of Solids and Structures, 2014,11: 2333-2350.

[10] HAN Q, CHU F. Dynamic instability and steadt-state response of an elliptical cracked shaft [J]. Arch. Appl. Mech, 2012,82:709-722.

[11] SHIN C S, CAI C Q. Experimental and finite element analyses on stress intensity factors of an elliptical surface crack in circular shaft under tension and bending [J]. International Journal of Fracture, 2004,129:239-264.

[12] CARPINTERI A, BRIGHENTI R, SPAGNOLI A. Surface flaws in cylindrical shafts under rotary bending [J]. Fatigue & Fracture of Engineering Material & Structure, 1998,21: 1027-1035.

Bending stiffness model of a breathing elliptical cracked rotor

LIU Zheng, WANG Jianjun

(School of Energy and Power Engineering, Beihang University, Beijing 100191, China)

Usually a fatigue crack on a rotor shaft has an elliptical tip, while the current literatures at home and abroad mostly focus on straight-tip crack rotors, very few articles built models to study elliptical-tip crack breathing behavior. Here, a new breathing model of an elliptical crack on a cylindrical shaft was proposed to modify the neutral axis’s position and determine crack open area. Based on the crack strain energy, the elliptical crack’s additional flexibility coefficient was calculated, and the bending stiffness model of the elliptical cracked rotor was also established. It was shown that the proposed crack’s breathing laws agree well with those of literatures and the finite element results, the crack’s additional flexibility and rotor’s dimensionless deflection both meet the requirements of computing, the effectiveness and feasibility of the model are validated.

cracked rotor; elliptical crack; breathing mechanism; bending stiffness

2015-07-10 修改稿收到日期：2015-10-24

刘政 男，硕士生，1991年生

王建军 男，博士，教授，1956年生

TH113.1

A

10.13465/j.cnki.jvs.2016.21.029