一种新型自复位耗能拉索支撑的理论研究与数值分析
2016-12-15LIEW
池 沛, 董 军, 彭 洋, LIEW J Y R,3
(1. 南京工业大学 土木工程学院,南京 211816;2.扬州大学 建筑科学与工程学院,扬州 225009;3. 新加坡国立大学 土木与环境学院,新加坡 117576)
一种新型自复位耗能拉索支撑的理论研究与数值分析
池 沛1,2, 董 军1, 彭 洋1, LIEW J Y R1,3
(1. 南京工业大学 土木工程学院,南京 211816;2.扬州大学 建筑科学与工程学院,扬州 225009;3. 新加坡国立大学 土木与环境学院,新加坡 117576)
传统的支撑框架体系通过材料的塑性屈服耗散地震能量,在震后往往产生较大的残余变形,不仅修复代价高昂,更会严重危害结构的使用安全。提出了一种新型支撑形式——自复位耗能拉索支撑,可在特定的地震水准下降低刚度,耗散地震能量,同时利用复位筋提供的恢复力消除支撑残余变形。对其构造和工作原理进行了详细的说明,建立了力学分析模型,理论推导了在单调荷载和往复荷载作用下的荷载-位移关系,提出了控制参数的计算方法。建立了ABAQUS有限元模型,通过与理论分析结果对比验证了支撑的工作性能。研究结果表明在楼层层间位移角达到2%时,支撑仍然具有完全的自复位能力。提出的力学模型和数值模型可为此类支撑的设计提供理论基础。
抗震性能;自复位;耗能;支撑;预应力
支撑框架体系作为一类高效的抗侧力体系广泛应用于工程抗震领域,其中支撑的性能直接决定了体系的抗震性能。普通中心支撑在小-中震下能够维持较大的弹性刚度,但在强震作用下会产生屈曲现象,诱发节点板和支撑本身过早发生疲劳破坏,结构的延性和滞回性能较差[1-2]。特殊中心支撑[3-5]、偏心支撑以及屈曲约束支撑[6]利用节点板、耗能梁端或耗能内芯的屈服机制耗散地震能量,具有较强的非线性变形能力,但在震后会产生很大的不可恢复变形。
文献[7]的研究结果表明,当残余层间位移角超过0.5%时,结构的修复成本将超过重建成本,即不具有修复价值。此外,由残余变形引起的P-Δ效应将加剧结构的倒塌风险,对结构安全造成严重威胁[8]。鉴于残余变形对于结构性能具有重大影响,美国和欧洲在最新的基于性能(performance-based)的抗震设计规范中[9-10]明确阐明了控制该项指标的重要意义,并将其作为评估结构震后性能的关键参数。
加拿大学者CHRISTOPOULOS等[11]首先提出了在支撑中引入后张预应力筋消除残余变形的方法,研制了自复位耗能(Self-Centering Energy-Dissipative, SCED)支撑,并进行了全尺试件的可行性验证试验,结果表明支撑的承载力在800 kN左右,层间位移角在2%以内可以实现完全自复位,耗能能力良好。刘璐等[12]提出了自复位屈曲约束支撑,通过预应力钢绞线消除支撑的塑性变形,拟静力试验结果表明预应力施加和保持的工艺是决定复位效果的关键因素。文献[13-14]提出了双核心SCED支撑,通过将两个自复位系统进行串联,成倍提高了支撑的复位能力。文献[15]通过试验发现支撑的受力性能对于制造误差非常敏感,试验得到的初始刚度仅为理论分析的60%。文献[14]进一步通过分析指出,当内外套管长度存在三千分之一的制造误差时,支撑的初始刚度将显著下降。
现有的SCED支撑由于构造的特殊性导致初始刚度偏大,支撑较为刚劲,增大了结构的地震作用。支撑性能对于制造误差十分敏感,加工工艺要求苛刻,对其推广应用造成了一定限制。为克服现有SCED支撑的不足,作者提出了一种新型SCED拉索支撑。本文首先阐述了该支撑的构造形式及工作原理;然后理论推导了在单调荷载和往复荷载作用下的荷载-位移关系,提出了控制参数的计算方法;最后通过将数值模型与理论分析的结果进行对比验证了支撑的工作性能。
1 SCED拉索支撑的构造及工作原理
1.1 SCED拉索支撑的构造
如图1所示,SCED装置(共2套)平行安装在框架梁上,每套与一道高强钢索连接组成SCED拉索支撑作为结构的主要抗侧力部件,在框架梁的两端安装滑轮引导钢索走向。由于钢索的单拉特性,对于特定方向荷载作用下的非受力钢索用虚线表示。
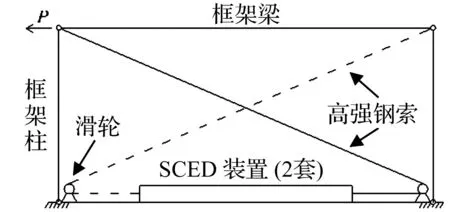
图1 SCED拉索支撑框架体系Fig.1 SCED tension-only-braced frame
SCED装置的基本构造如图2所示,复位筋采用后张法建立预应力并锚固在限位板上(图2(b))。上锚固端头由于始终只受到来自复位筋向左的拉力,且由于限位板的作用,因此相当于复位筋的一个不动支座。下锚固端头与摩擦消能件相连,当作用在高强钢索上的荷载增大到一定程度时,允许其向右运动,进一步拉伸复位筋。
摩擦消能件由钢板和黄铜板交替组成,通过对拉式高强螺栓提供法向压力。位于消能件中央的摩擦板(钢板)开设长槽孔,允许其在板件长度方向上滑动,槽孔的长度根据摩擦板的允许位移计算确定;两侧其余4块板件均开圆孔,通过外板与底座栓接固定。
装置内滑轮的作用主要是增加复位筋的长度,降低材料的弹性变形要求,提高复位能力。

图2 SCED装置构造Fig.2 SCED device schematic
1.2 SCED拉索支撑的工作原理
如图3(a)所示,将复位筋、摩擦板和钢索分别理想化为线刚度为Kt、Kf和Kc的弹簧,摩擦板的最大静摩擦力为F。复位筋初始态(图3(b)的O点)的预拉力为Tt,0,Tt,0经限位板R传至装置底座。限位板用以平衡预拉力的反作用力,同时限制摩擦板向左滑动。
在循环荷载作用下,SCED拉索支撑的滞回关系可用图3(b)来描述,图中P为作用于钢索上的荷载,Δ为钢索的端部位移。当P的数值较小时(OA段),钢索另一端由于受到预拉力Tt,0和摩擦力的作用相当于固定端,因此SCED装置不能发挥作用。随着P的增大直至克服Tt,0+F(A点),SCED装置启动,摩擦消能件开始工作。此时由于钢索和复位筋为串联状态,支撑的整体刚度下降(即“屈服”),抑制地震力的快速增长,从而避免了梁柱等主体构件的损坏。从B点开始卸载时,支撑在复位筋的作用下,变形不断减小直至恢复原位(O点)。反向加载过程OA′B′C′D′和正向加载过程OABCD类似。
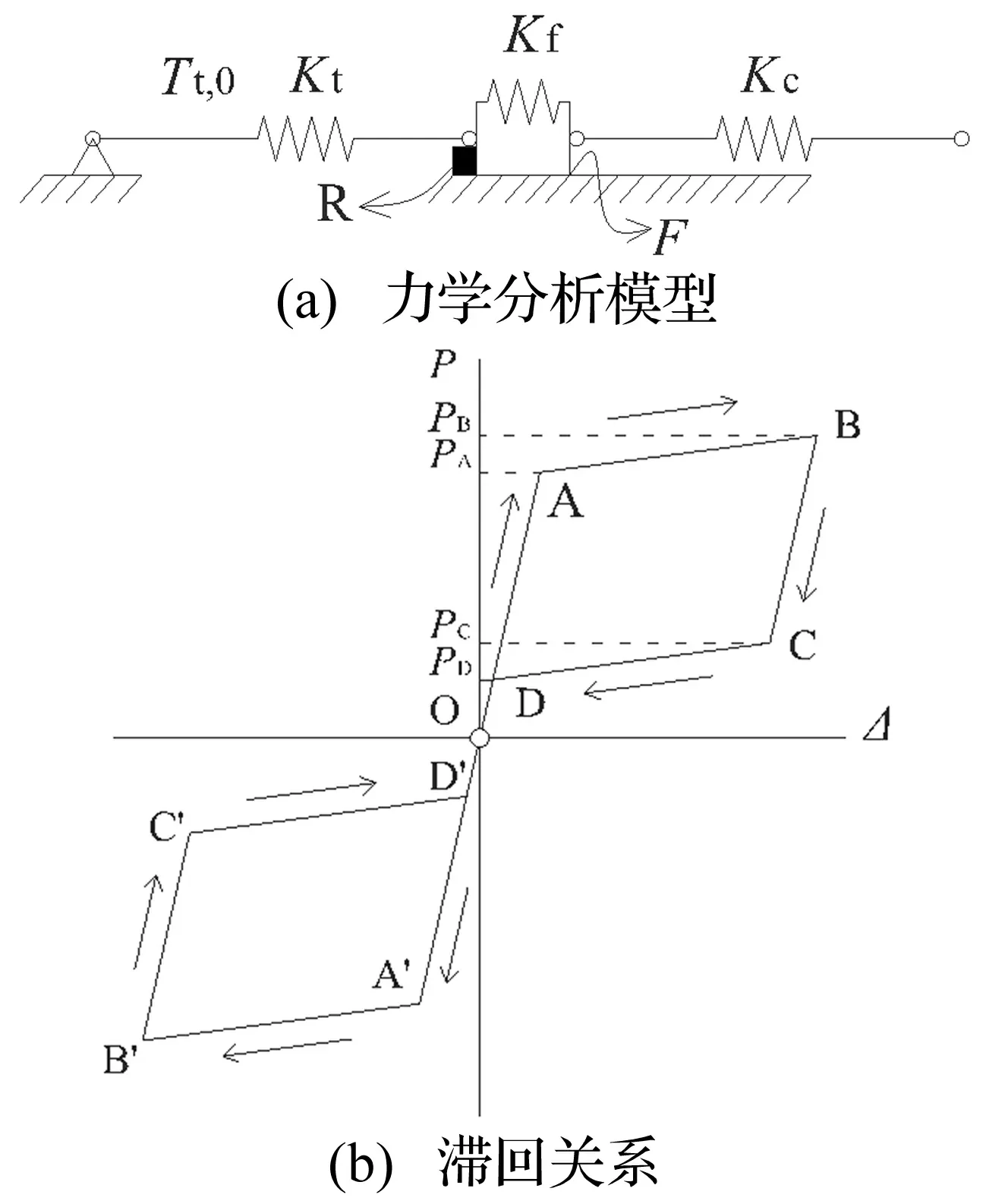
图3 SCED拉索支撑的工作机理Fig.3 Mechanics of the SCED tension-only brace
1.3 SCED拉索支撑的优点
相较于现有的SCED支撑,本文提出的支撑形式具有以下优点:
(1) 显著降低地震作用。现有的SCED支撑中受压套筒的设计由稳定控制,而双核心SCED支撑的初始刚度很大,对抗震不利。本文所述的支撑形式采用全拉力系统,不存在稳定问题,可充分发挥高强钢索的抗拉能力,减小支撑截面积,结构更加轻柔。
(2) 启动条件可控。通过调整消能件螺栓的预紧力控制SCED装置的启动条件,当结构达到设计侧移值时即开始工作,可实现基于性态/位移的抗震设计目标。
(3) “屈服”刚度可设计。支撑的“屈服”刚度可通过改变复位筋的线刚度加以调整,避免屈服刚度过低导致位移向率先屈服楼层集中,使结构抗侧刚度沿高度方向分布更加合理。
(4) 消除制造误差的不利影响。SCED拉索支撑抛弃了现有SCED支撑内、中、外筒连环套嵌的构造形式,复位筋直接锚固在限位板上,克服了制造误差问题。
(5) 无焊接。板件连接全部采用螺栓连接,避免了焊接对预应力的破坏,保证自复位效果。
(6) 安装便捷。SCED装置固定后,只需与拉索连接即可,安装快速便捷,且无须改变主体结构的建造方式。
2 SCED拉索支撑的理论分析
2.1 理论推导
采用图4所示的力学模型对SCED拉索支撑进行单向受拉分析。SCED拉索支撑的I端与框架梁栓接固定,J端承受轴向荷载P。限位板R用以限制摩擦板向左滑动,同时平衡复位筋的预拉力Tt,0。
图中复位筋的线刚度:
(1)
式中:Et、lt,0和At,i分别表示复位筋的弹性模量、初始长度和第i根复位筋线材的截面积。
摩擦板的线刚度:
(2)
式中:Ef、lf和Af分别表示摩擦板的弹性模量、长度和截面积。
高强钢索的线刚度:
(3)
式中:Et、lc,0和Ac,i分别表示高强钢索的弹性模量、初始长度和第i根钢索线材的截面积。
由图4(a)可知,当荷载P克服最大摩擦力F和预拉力Tt,0之和时,摩擦板可以发生相对滑动,设此时的荷载为启动荷载Pa,则有:
Pa=F+Tt,0
(4)
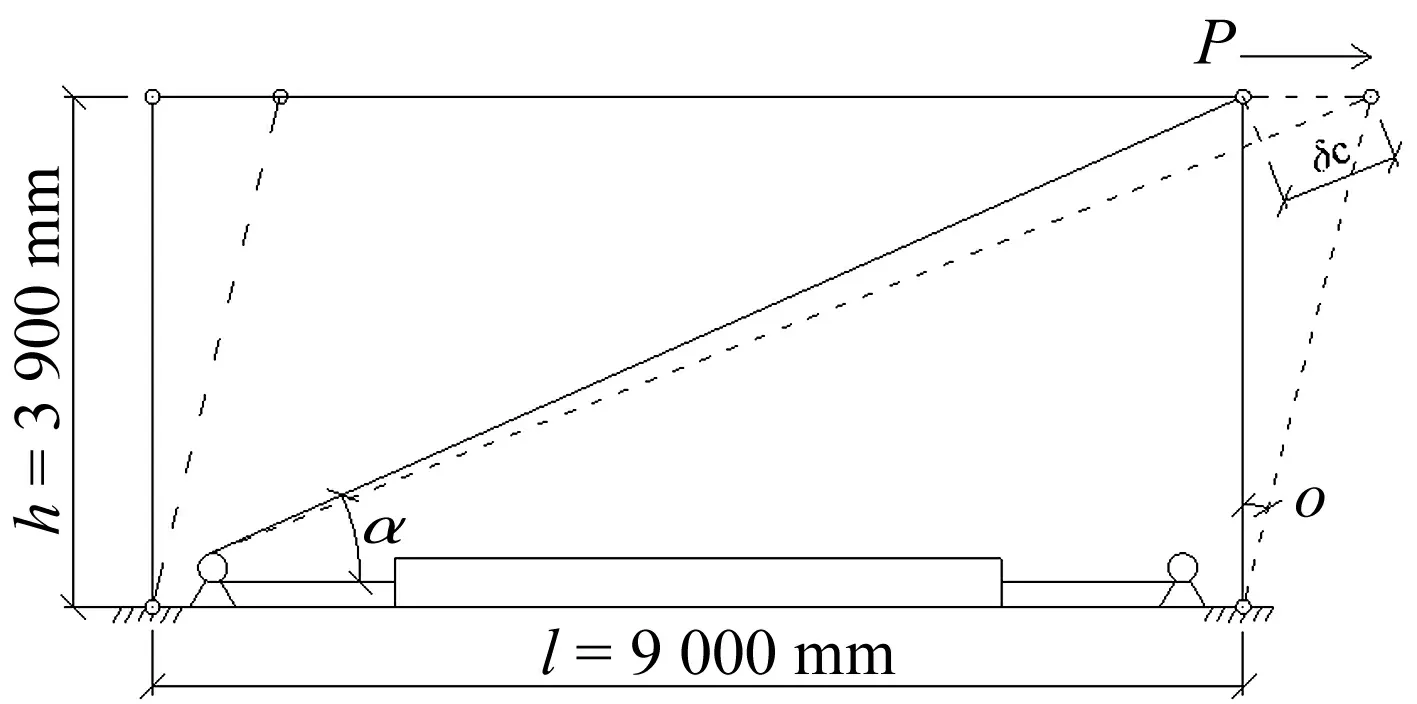
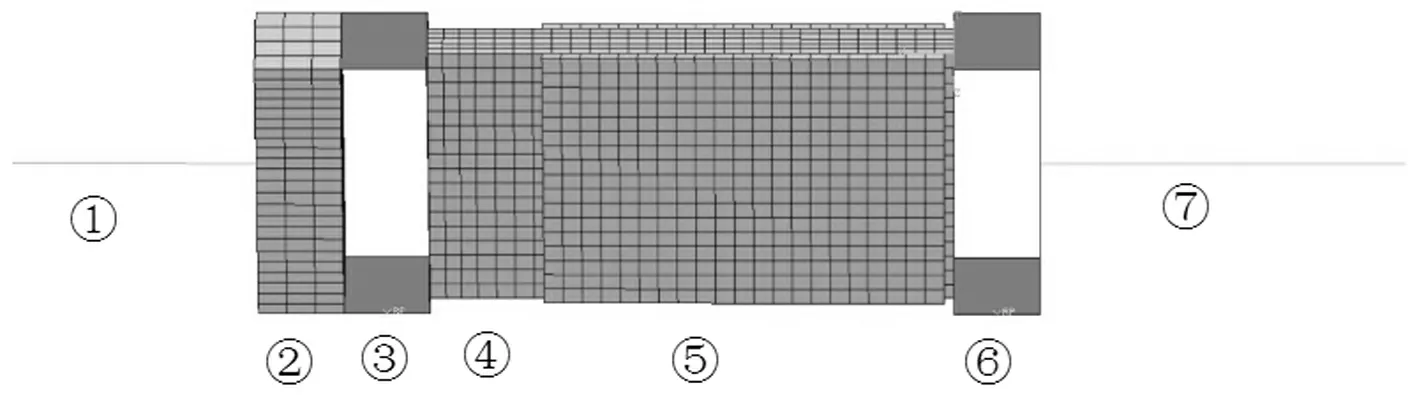
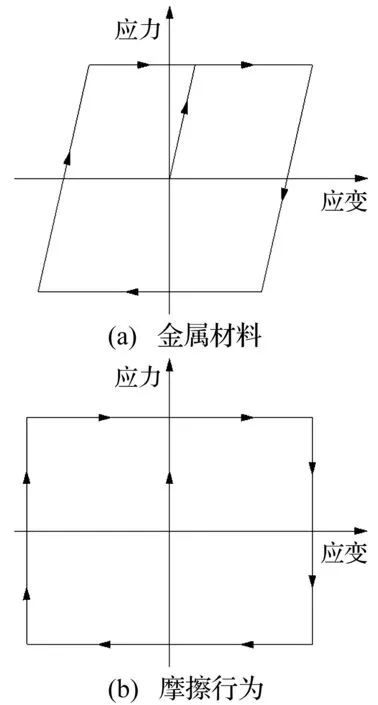
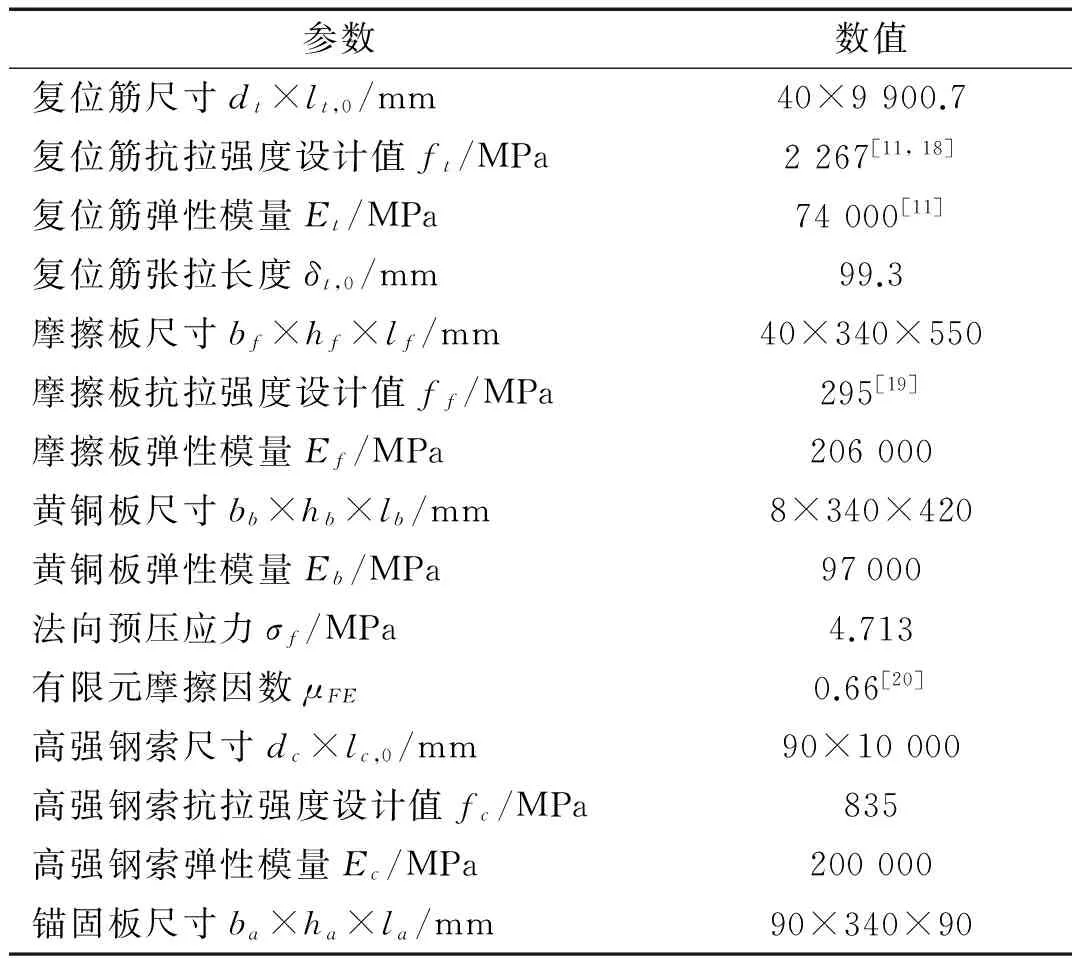
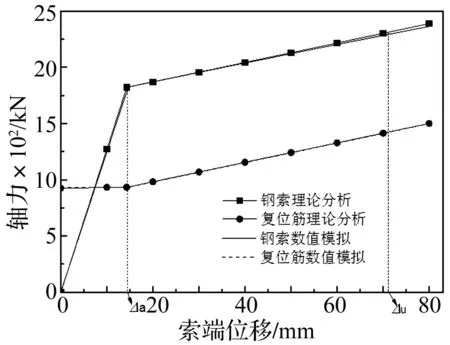
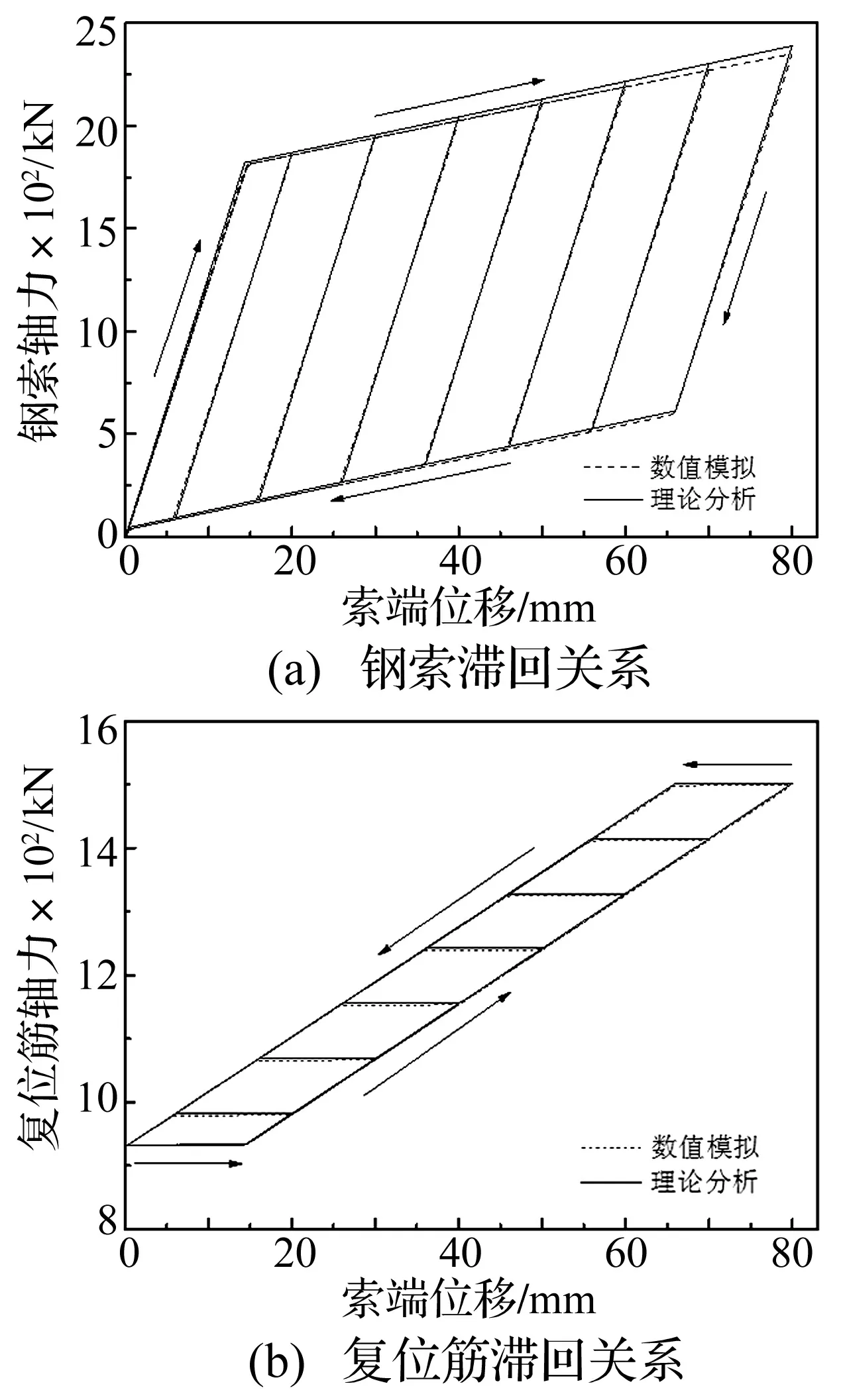
① 当P K0=Kc (5) OA段钢索的拉力Tc为: Tc=Kcδc=K0Δ (6) 式中:δc为钢索的伸长量;Δ为钢索的端部位移。 OA段复位筋的拉力Tt为: Tt=Tt,0 (7) ② 当荷载增大至P≥Pa时(图4(b)所示AB段),钢索拉力克服F和T0的合力并与复位筋串联,此时SCED拉索支撑的启动刚度Ka为: Ka=(1/Kt+1/Kf+1/Kc)-1 (8) AB段钢索的拉力Tc为: Tc=Pa+Ka(Δ-Δa) (9) 式中:Δa为SCED拉索支撑的启动位移。 AB段复位筋的内力Tt为: Tt=P-F (10) AB段复位筋的伸长量为: δt=(Tt-Tt,0)/Kt (11) ③ 若从B点处开始卸载(图4(c)所示BC段),摩擦力将首先通过改变大小和方向平衡卸载值,直至摩擦力的大小改变为-F为止(C点),这一过程中摩擦板始终处于静止状态。因此有: PB-PC=2F (12) 在这一阶段支撑刚度恢复为初始刚度K0,复位筋的拉力Tt保持不变。在B点处,复位筋、摩擦板和高强钢索的拉力同时达到最大值,为强度设计的控制状态。 ④ 当卸载值超过2F时(图4(d)所示CD段),摩擦板将在复位筋作用下向初始位置滑动,同时带动钢索复位至D点与限位板接触。在这一阶段中,钢索和复位筋再次串联,刚度恢复至启动刚度Ka。 为实现自复位功能,消除残余变形,由图4可知应满足PD≥0,即: PA-2F≥0 (13) 可解得: Tt,0≥F (14) 定义复位耗能系数 β=Tt,0/F (15) 将式(15)代入式(14)得: β≥1 (16) 即为使结构实现自复位,必须保证β≥1。 ⑤ DO段只有拉索发挥作用,SCED装置不工作。 图4 各阶段工作机理Fig.4 Detailed mechanics for whole behavioral stages 2.2 控制参数计算 启动荷载Pa决定了SCED装置的启动条件。为实现基于位移的控制目标,使装置在设定的结构变形状态下工作,需要选择适当的Pa值。 如图5所示,在侧向荷载P的作用下,框架将发生剪切变形,其中钢索支撑发生的轴向变形为: δc=hθcosα (17) 式中:h为楼层高度;θ为层间位移角;α为钢索与水平方向的夹角。 图5 SCED拉索支撑变形与楼层侧移的关系Fig.5 Shear strain of proposed system 根据钢索的变形量计算得到启动荷载: Pa=Kcδc=Kchθcosα (18) 在本文中,取θ=[θe]=0.004 rad[16],即设定结构在达到多遇地震作用下的弹性层间位移角限值[θe]时开始“屈服”。图5中的钢索直径dc=90 mm,长度lc,0=10 000 mm,弹性模量Ec=200 GPa。计算得到Pa=1 821.21 kN。 需要指出的是,在实际情况中可根据变形要求调整钢索刚度,使SCED装置在结构发生较小变形时就开始工作,且这种调整是灵活的、可设计的。 将式(15)代入式(4)可解出: F=(1+β)-1Pa (19) Tt,0=(1+β-1)-1Pa (20) 计算得到在图4所示的半个循环内通过摩擦耗散的能量为: (21) 对于特定的受力变形状态,式(21)中的Pa、PB和Kt都为定值,ED将随着β的减小而增大。因此在保证自复位的前提下(式16),要提高支撑的耗能能力,β因尽量取小。在本文中β取1.05,相应的摩擦力F=888.38 kN,复位筋预拉力Tt,0=932.83 kN。 3.1 有限元建模方法 SCED拉索支撑的力学行为较为复杂,为验证理论分析的正确性,基于ABAQUS平台建立了有限元分析模型,如图6所示。限位板、摩擦板和黄铜板之间的接触关系具有强非线性特征,根据接触属性,全部采用C3D8I单元(一阶六面体非协调模式单元)。高强钢索和复位筋采用T3D2(一阶三维桁架单元)模拟单轴受力特性。复位筋锚板和高强钢索锚板的作用主要是将作用于点上的集中力均匀地传递到接触面,全部采用解析刚体进行模拟。 ①复位筋;②限位板;③复位筋锚板;④摩擦板;⑤黄铜板;⑥高强钢索锚板;⑦高强钢索图6 SCED拉索支撑的有限元模型Fig.6 FE model of the SCED tension-only brace ①和③、④和⑥、⑥和⑦分别采用绑定约束,始终保证各接触对紧密接触。②和③之间建立无摩擦接触,③可自由向右发生滑动,但向左运动会受到②的限制。④和⑤之间建立有限滑移摩擦接触,接触压力和间隙的关系设置为“硬接触”。金属的材料属性定义为理想的弹塑性应力应变关系(图7(a)),遵循Von Mises屈服准则;摩擦行为采用经典库伦摩擦模型描述[11,17](图7(b))。 图7 本构关系Fig.7 Constitutive relations 为使模型简化,只对1个摩擦消能件建模,所以模型中的摩擦面数量(2个)为实际摩擦面数量(4个)的一半。为保证模型中各部件受力与实际情况一致,将有限元摩擦因数放大1倍处理,即μFE=2μ,其中μ为钢与黄铜的摩擦因数。摩擦板上施加的法向预压力为Nf=F/2μFE。同理,摩擦板在垂直于钢索平面上的截面积也需增大1倍,即Af,FE=2Af。 对复位筋采用支座位移法施加预拉力Tt,0。首先在①和③之间建立绑定约束关系;然后限制住②的所有自由度;最后在①的另一端采用铰接支座,并对其施加定量位移荷载(即张拉长度):δt,0=Tt,0/Kt。 有限元模型中各部件的几何、物理参数详见表1。 3.2 数值模拟与理论分析的比较 由图5所示的几何关系得到钢索端部位移Δ与层间位移角θ的关系为: Δ=3.58×103θ (22) 为考察SCED拉索支撑在罕遇地震作用下(θu=0.02 rad[16],相应的Δu=71.60 mm)的力学性能,首先对其进行单调加载,加载过程以Δ为控制参数,令最大端部位移Δmax=80 mm>Δu。 根据本文第二节的力学模型,计算得到单调荷载作用下钢索轴力和复位筋轴力的数值,并与有限元结果进行对比,如图8所示。从图中可以发现,理论分析与数值模拟的数值在启动位移Δa处基本重合,说明数值模拟能够精确地捕捉到SCED装置的启动条件,但前提条件是必须选择合适的增量步。当索端位移超过启动位移Δa后,复位筋的轴力将与钢索轴力同步增长,二者的差值为最大摩擦力F。达到Δu后,钢索和复位筋的轴力都没有超越屈服力,表明在楼层层间位移角达到2%时,支撑仍然具有完全自复位能力。 表1 有限元模型各部件参数 图8 SCED拉索支撑的单调加载特性Fig.8 Monotonic behavior of the SCED tension-only brace 图9显示了支撑在受拉区间内的滞回关系,图中箭头表示加卸载的路径。Δ的幅值Δi=10imm,i=1,2…,8。对于钢索(图9a),加载阶段支撑“屈服”后刚度的理论值为8.65 kN/mm,稍大于模拟值(8.53 kN/mm);最大荷载的理论值(2 389.41 kN)比模拟值(2 350.21 kN)大1.67%。对于复位筋(图9b),其理论值与模拟值基本完全重合。各加卸载循环后,钢索的端部位移全部回归到0,实现了完全自复位。 图8、图9的理论分析与数值模拟的结果总体上吻合良好,验证了数值模型的准确性,可为下一步的参数分析提供基础。 图9 SCED拉索支撑的滞回特性Fig.9 Hysteretic behavior of the SCED tension-only brace 本文提出了一种新型SCED拉索支撑,并建立了力学模型,通过理论分析和数值模拟研究了支撑在单调荷载和往复荷载作用下的力学性能,得到以下几点主要结论: (1) SCED拉索支撑是一套全拉力系统,克服了现有SCED支撑稳定问题突出的缺点,可以有效减小支撑截面积,降低地震作用。 (2) SCED装置工作后,钢索与复位筋串联降低支撑刚度,抑制地震力快速增长,同时利用摩擦机制耗散地震输入的能量。支撑的“屈服”刚度具有可设计性,为优化罕遇地震作用下结构的刚度分布提供了设计可行性。 (3) 通过理论推导得到了支撑在单调荷载和往复荷载作用下的滞回关系,提出了控制参数的计算方法,可为此类支撑的设计以及整体结构的分析提供理论基础。 (4) 有限元模拟结果与理论推导结果吻合良好,验证了建模方法的准确性。数值结果表明在楼层层间位移角达到2%时,支撑扔具有完全自复位能力。 [1] Seismic provisions for structural steel buildings:ANSI/AISC 341—10[S]. Chicago: American Institute of Steel Construction, 2010. [2] 熊二刚, 张倩. 中心支撑钢框架结构基于性能的塑性抗震设计 [J]. 振动与冲击, 2013, 32(19): 195-204. XIONG Ergang, ZHANG Qian. Performance-based plastic design method for steel concentrically braced frames [J]. Journal of Vibration and Shock, 2013, 32(19): 195-204. [3] HSIAO P C, LEHMAN D E, BERMAN J W, et al. Seismic vulnerability of older braced frames [J]. Journal of Performance of Constructed Facilities, 2014, 28(1): 108-120. [4] AKBAS B, SUTCHIEWCHARN N, CAI W, et al. Comparative study of special and ordinary braced frames [J]. The Structural Design of Tall and Special Buildings, 2013, 22(13): 989-1022. [5] 李慎, 苏明周. 基于性能的偏心支撑钢框架抗震设计方法研究[J]. 工程力学, 2014, 31(10): 195-204. LI Shen, SU Mingzhou. A performance-based seismic design method for eccentrically braced steel frames [J]. Engineering Mechanics, 2014, 31(10): 195-204. [6] ZHAO J, WU B, OU J. Flexural demand on pin-connected buckling-restrained braces and design recommendations [J]. Journal of Structural Engineering, 2012, 138(11): 1398-1415. [7] MCCORMICK J, ABURANO H, IKENAGA M, et al. Permissible residual deformation levels for building structures considering both safety and human elements [C] // The 14 World Conference on Earthquake Engineering, Beijing, China: Chinese Association of Earthquake Engineering, 2008. [8] EROCHKO J, CHRISTOPOULOS C, TREMBLAY R, et al. Residual drift response of SMRFs and BRB frames in steel buildings designed according to ASCE 7-05 [J]. Journal of Structural Engineering, 2011, 137(5): 589-599. [9] FEMA 445 Next-generation performance-based seismic design guidelines: program plan for new and existing buildings [S]. Washington DC, USA: Federal Emergency Management Agency, 2006. [10] Eurocode 8: Design of structures for earthquake resistance [S]. Brussels, Belgium: European Committee for Standardization, 2013. [11] CHRISTOPOULOS C, TREMBLAY R, KIM H J, et al. Self-centering energy dissipative bracing system for the seismic resistance of structures: development and validation [J]. Journal of Structural Engineering, 2008, 134(1): 96-107. [12] 刘璐, 吴斌, 李伟, 等. 一种新型自复位防屈曲支撑的拟静力试验 [J]. 东南大学学报(自然科学版), 2012, 42(3): 536-541. LIU Lu, WU Bin, LI Wei, et al. Cyclic tests ofnovel self-centering buckling-restrained brace [J]. Journal of Southeast University (Natural Science Edition), 2012, 42(3): 536-541. [13] EROCHKO J, CHRISTOPOULOS C, TREMBLAY R. Design and testing of an enhanced-elongation telescoping self-centering energy-dissipative brace [J]. Journal of Structural Engineering, 2015, 141(6): 04014163. [14] CHOU C C, CHEN Y C, PHAM D H, et al. Steel braced frames with dual-core SCBs and sandwiched BRBs: mechanics, modeling and seismic demands [J]. Engineering Structures, 2014, 72(72): 26-40. [15] EROCHKO J, CHRISTOPOULOS C, TREMBLAY R. Design, testing, and detailed component modeling of a high-capacity self-centering energy-dissipative brace [J]. Journal of Structural Engineering, 2015, 141(8): 04014193. [16] 建筑抗震设计规范:GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010. [17] CHOPRA A K.结构动力学:理论及其在地震工程中的应用 [M] .北京:清华大学出版社,2007. [18] ZOGHI M. The international handbook of FRP composites in civil engineering [M]. Boca Raton: CRC Press, 2014. [19] 钢结构设计规范: GB 50017—2003[S]. 北京: 中国计划出版社, 2003. [20] SONG L l, GUO T, CHEN C. Experimental and numerical study of a self-centering prestressed concrete moment resisting frame connection with bolted web friction devices [J]. Earthquake Engineering and Structural Dynamics, 2014, 43(4): 529-545. Theoretical analysis and numerical simulation for an innovative self-centering energy-dissipative tension-brace system CHI Pei1,2, DONG Jun1, PENG Yang1, Richard, LIEW J Y R1,3 (1.College of Civil Engineering, Nanjing Tech University, Nanjing 211816, China; 2.College of Architectural Science and Engineering, Yangzhou University, Yangzhou 225009, China;3.Department of Civil and Environmental Engineering, National University of Singapore, Singapore 117576, China) A conventional braced frame system dissipating seismic energy through its material’s plastic yield produces larger permanent deformations after major earthquakes. Such permanent deformations affect the structural safety and they are cost to repair. To avoid this drawback, a new tension-brace system capable of self-centering and dissipating energy was proposed. For a given seismic intensity, the proposed system was capable of reducing its stiffness in order to dissipate energy and provide a restoring force to reduce the permanent deformations. The key structure and working principle of the self-centering tension-brace system were presented. The mechanical analysis model was developed to derive the load-displacement relationships under monotonic and cyclic loads. The performance of the tension-brace system was further investigated by using nonlinear finite element software ABAQUS. The analysis results showed that the tension-brace system can still have a full ability of self-centering when the storey drift angle exceeds 2.0%. Both the theoretical and numerical models provided necessary tools and a theoretical basis for designing the proposed self-centering energy-dissipating tension-brace system. seismic performance; self-centering; energy-dissipation; brace; prestress 国家留学基金委资助项目(201408320150) 2015-09-09 修改稿收到日期:2015-11-07 池沛 男,博士,讲师,1987年生 董军 男,博士,教授,1964年生 E-mail:dongjun@njtech.edu.cn TU352.1 A 10.13465/j.cnki.jvs.2016.21.027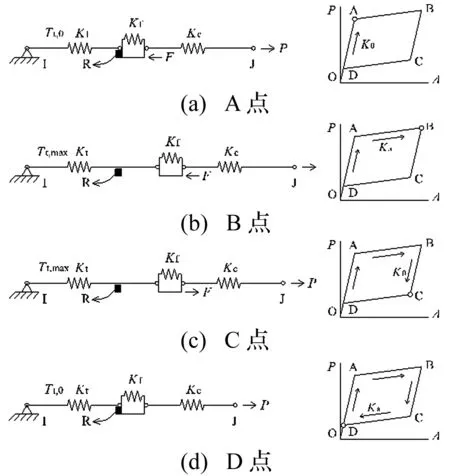
3 SCED拉索支撑的数值模拟
4 结 论
