电流变夹层振动控制和拓扑优化研究

陈春强, 陈 前

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)



电流变夹层振动控制和拓扑优化研究

陈春强, 陈 前

(南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016)

为电流变夹层板设计了半主动的变刚度控制算法，并对其进行了夹层结构的拓扑优化。首先，建立了电流变夹层结构的动力学模型，基于开关控制策略发展了适用于ER夹层板的模态控制算法。随后，构造了电流变夹层结构的单阶模态和综合模态的频率变化率为优化目标函数，再采用粒子群优化方法，以这两个函数为目标，对结构进行了拓扑优化，并且得到了一定材料使用率限制下相应的拓扑布置构形。最后，采用变刚度控制的等效阻尼比和多种激励下的时域响应对比两种手段对拓扑优化的结果进行了验证，数值算例证实了该拓扑优化结果以及变刚度控制的有效性。

电流变夹层板；模态频率变化率；粒子群优化；拓扑优化；等效阻尼比

电流变液夹层板(Electrorheological sandwich plate，ER夹层板)是一种振动控制新型的智能结构，这种结构可实现被动(加载恒定电场或不加载电场)/半主动控制技术一体化，具有集被动控制安全、可靠和半主动控制适应性强、控制效果显著的优点于一体，特别是半主动控制技术能在较小的能量代价下，具有优越的减振、降噪性能。最早的ER夹层结构的探索开始于CHOI等[1]。后来，YALCINTAS等[2]分析了ER夹层梁的动力学特性，讨论厚度对模态损耗因子的影响。孟光等[3-4]对ER夹层梁、板结构也有相关的建模、实验研究，分析了电场强度、厚度比等对结构特性的影响，得到了丰富的结论。近年来，YEH等[5]研究则关注了ER夹层梁、矩形板以及环形板等结构。JAFAR等[6]则讨论边界约束条件对ER夹层结构瞬态响应的影响，电场增强瞬态响应线性衰减，可见众多的研究还是集中在试图通过施加外场，提高结构阻尼从而达到减振的目的。

另一方面，作为一种新的智能振动控制技术，其在实际工程应用上还有几个关键问题未能解决，例如适用于无限自由度系统的半主动控制算法、在材料利用率限定条件下拓扑优化等。事实上，半主动控制算法来源于主动控制策略或振动响应分析，并且在悬架机构、建筑抗震等领域已有相当的实际应用[7]，只是算法都是应用在单自由度系统，对耦合系统考虑得较少。粒子群优化(Particle Swarm Optimization Algorithm，PSO)在模式识别[8]、控制优化[9]和任务分配等优化领域得到广泛应用，研究[8]指出相对于GA方法，PSO方法具有更快的收敛速度，从而能节约计算资源。作为一种智能优化算法，PSO方法也被用于结构的拓扑优化[10-11]。总之，对于ER夹层结构，控制算法设计和拓扑优化工作还很少见。

采用零场振型对控制系统进行解耦，在此基础上开发了新的变刚度控制算法，并且在限定的ER材料使用率条件下进行拓扑优化。首先，基于单自由度的开关控制策略发展了适用于板的变刚度模态控制算法。随后，基于粒子群优化方法，以电流变夹层结构的单阶模态和综合模态的变刚度性能最优为目标，对结构进行了拓扑优化，并且给出了相应的拓扑构形。最后，采用了数值方法验证了控制算法的有用性和优化构形的合理性。

1 系统模型

如图1所示的电流变液夹层板振动控制系统，将ER夹层处划分为4节点7自由度单元，而无ER处划分为4节点5自由度板单元，限于篇幅，有限元建模过程从略，得到如下的ER夹层板系统的控制方程：

(1)

式中:零电场下的复刚度矩阵K*=K1+jK2，G(E)是由外加电场强度决定的刚度变化系数阵。

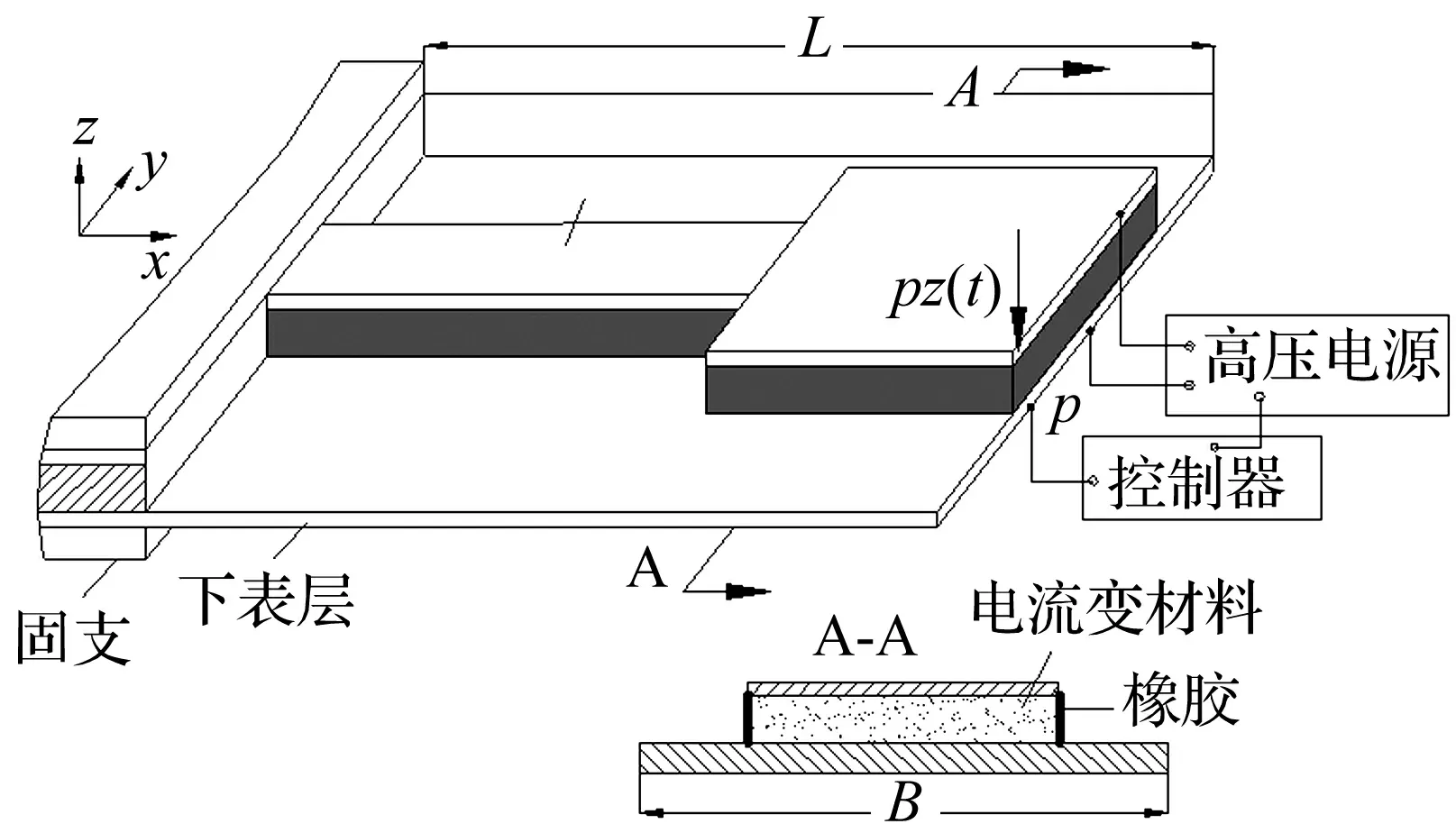
图1 电流变夹层板振动控制系统Fig.1 The orthotropic sandwich plate with an ER fluid core and a constraining layer

2 模态控制算法

2.1 算法设计准备

开关控制算法[12](Bang-Bang control，also called On-Off control)，是变刚度控制(Active Variable Stiffness，AVS)中最成熟的算法，其以位移和速度输入，当两者符号一致时，控制输出为1，系统附加上刚度；否则控制输出为零，即撤去附加刚度，从而舍弃相应的弹性应变能。从以上描述可知，变刚度控制利用是刚度实部的变化，那么可以做以下模型简化，略去刚度的虚部，即

(2)

记Φ是K1、M的关于M归一化了的特征向量阵，用δ=ΦQ变换上式，并两端左乘ΦT，可得：

ΦTK1G(E)ΦTQ=ΦTF

(3)

式中:左边两项的系数矩阵均是对角阵，第三项系数阵ΦTK1G(E)ΦT一般而言不会是严格对角的，但研究[3]表明，ER夹层板结构的固有振型基本不随电场强度变化而变化，这说明用任意电场工况下的振型进行解耦，得到的第三项系数阵也是对角占优的，略去其非对角元素，有：

(4)

式中:fi是ΦTF向量的i元素，qi(t)是近似的实模态坐标，控制中该值由Q(t)=ΦTMδ(t)获得，其中ΦTM是控制前获得的系统参数，δ(t)则在控制中每个采样周期内实测而得。

在控制算法设计之前，系统相关的参数，如质量矩阵M、刚度矩阵K1以及包含主要振动能量的前p阶模态的振型φ1,φ2,…,φp，应当首先获得。那么相应阶次的模态质量、模态刚度就能获知：

(5)

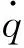
(6)

2.2 模态算法

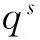
(7)

式中:Us通过式(6)获得。

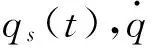
(8)

按照式(5)的分析，综合考虑到前p阶次模态的输出要求，控制器输出电场的综合平均值为：

(9)

式中:Qs是权重系数向量Q中的元素。

考虑到电场强度有其边界条件限制，即不能超过最高强度Eb且保持非负，所以半主动模态控制算法(semi-active modal control algorithm)的输出的控制电场是：

(10)

3 拓扑优化

3.1 优化目标函数

一般地，减振结构的优化目标是明确的，阻尼比即是目标函数，但这里的优化目标是ER夹层结构在变刚度控制下具有最优的减振效果，所以首先需要构造一个目标函数。早期的变刚度控制可追溯到KOBORI[12]，之后有学者指出变刚度控制效果与变刚度变化率、固有频率变化率的关系。用AVS控制的等效阻尼比表达其振动控制效果：

(11)

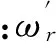
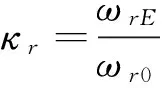
(12)

一般的，结构前几阶模态涵盖了系统的大部分振动能量，所以考虑前n个模态，构造综合模态频率变化率作为拓扑优化的适应值：

(13)

式中,Q1,Q2…Qn是模态权重向量QT的元素, 可以对不同工况条件配比不同的模态权重，以利于着重体现某些模态的影响。式(12)和式(13)给出了单阶和综合模态两种拓扑优化的目标函数。

3.2 粒子群优化

粒子群优化算法(Particle Swarm Optimization，PSO)将每个个体看成搜索空间中以速度飞行的一个微粒，由M个粒子组成的群体在D维空间中，其中第i个粒子的标准速度进化方程为：

si(t+1)=si(t)+Vi(t+1)

(14)

Vi(t+1)=λVi(t)+c1r1(Pi(t)-

si(t))+c2r2(Pg(t)-si(t))

(15)

式中,si,Vi,Pi(i=1,2,…,M) 和Pg均为D维的向量，si(t)和Vi(t)分别是i粒子的第t代的位置和速度，Pi(t)和Pg(t)分别是i粒子和群体历史最优位置，c1和c2分别是粒子认知系数和社会系数，r1和r2是[0,1]上均匀分布的随机数，λ是惯性权重。

3.3 ER夹层板的拓扑优化

在如图(1)所示的ER夹层板(a×b)上布置Ng个电流变层单元，第j个单元的位置坐标为(xj,yj)，在离散坐标下xj,yj(j=1,2,…,Ng)均是自然数，相应的搜索空间为2Ng维，每个粒子代表着一种布置方案。假设粒子群的规模为M，则式(19)中第i个粒子的相关向量为：

(16)

式中:第i粒子的向量si(或Vi或Pi或Pg)由水平分向量Xi(或Vxi或Pxi或Pxg)和垂直分向量Yi(Vyi或Pyi或Pyg)组合而成，分向量的维度是ER单元个数Ng。

以式(12)和式(13)函数最大化为目标，建立电流变夹层结构的拓扑优化模型如下：

find:X,Y

Max:κrorκQ

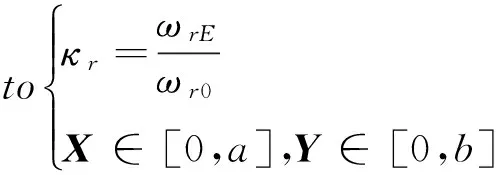
(17)

式中:以式(12)κr或式(13)κQ的值最大为优化目标，则式(15)中i粒子历史最优值Pi和粒子群最优值Pg的更新方式为：

(18)

或者

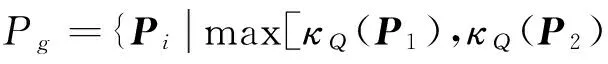
(19)

这里,i=1,2…,M。

利用上述的标准粒子群优化算法实现电流变夹层单元的优化布置。参考RATNAWEERA[13]的结论，c1和c2随时间动态调整，c1从2.5线性减至0.5，而c2从0.5增至2.5。惯性权重采用线性递减权值(Linearly Decreasing Weight, LDW)策略，λmax=0.9,λmin=0.4。按照粒子群优化过程，进行随机初始化，限制Vxi(Vyi)的最大速度的绝对值为2，反复更新粒子群的位置直至两次最优适应值增幅小于0.1%或者最大迭代次数200，迭代停止。

4 数值结果和讨论

如图1所示，ER夹层板左边固支，其余三边自由，其几何、物理参数见表1，ER材料参数参考DON[14]的研究。

表1 ER夹层板的几何、物理参数

注意到，前几阶模态包含了结构大部分的振动能量，所以控制器的模态n取为3。为了便利，下面列出了优化中的相关参数：a=9,b=6,M=10,Ng=26,D=52,n=3,QT=[1,1,1]。图2给出了ER夹层结构的两类优化布置构形。图2(a), (b)和(c)分别是以第一、二和三阶模态频率变化率最大为目标的优化构形；而图2(d)是以综合模态频率变化率最大化为目标的优化构形，采用权重QT。

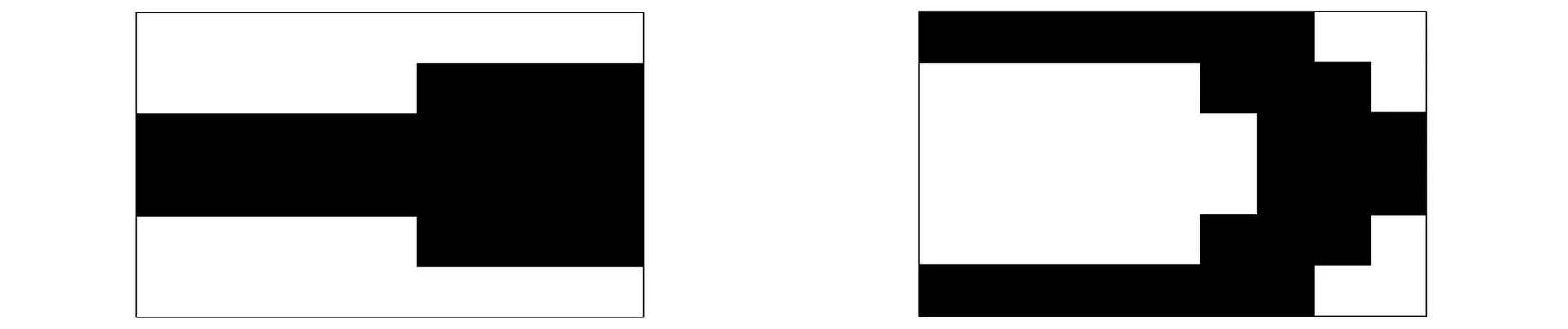
(a) Set1(1stmode)(b) Set2(2ndmode)

(c) Set3(3rdmode)(d) Set4图2 优化构形Fig.2Optimizationbymaximizingthemodalfrequencymobility

下面，讨论优化布置(Set1～4，材料利用率48%)对半主动控制效果的影响，主要采用等效阻尼比和时域响应对比两种手段。以满铺布置(Set0)为对照基准，等效阻尼比和综合阻尼比均列在表2中。根据式(11)计算各阶次模态的等效阻尼比ζ(eq)体现了变刚度控制的减振性能。从表中可知，针对各阶模态的优化构形获得了各自阶次的最大等效阻尼比。比如，Set1的第一阶等效阻尼比ζ1(eq)达到了0.075，这是Set0的等效阻尼值的65.2%，而在Set3的第三阶等效阻尼比ζ3(eq)是Set0时的68.8%。表中最后一列，是前三阶等效阻尼比与模态权重QT之积，优化布置中最大值0.113是Set4布置给出的，这也显示了综合模态最优布置的合理性。

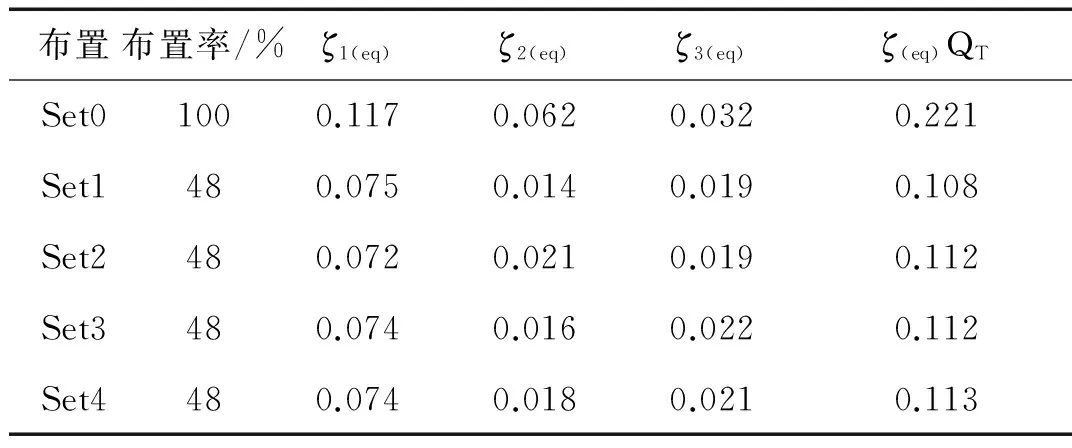
表2 多种构形在变刚度控制下的等效阻尼比

另外，在多种激励工况、多种优化构形下，时域响应对比可以更为直接显示控制效果。激励点和位移采集点均是自由度1/3处，如图1所示。所有工况下均采用式(10)的模态控制算法，时域响应对比如图3和4所示。采用第一、二阶模态频率附近的快扫频作为激励，同样的把满铺布置(Set0)设为对照基准，如图3(a)和(d)所示。p点处位移的均方根(RMSP)降幅用来评价优化布置的半主动控制减振效果。对比相关时域响应，可以得到几个结果。首先，变刚度控制能有效降低结构振动响应，比如Set0的RMSP 降幅达到了88.69%和88.29%，如图3 (a)和3(d)所示。第二，针对各阶模态的拓扑优化能在相应激励工况下取得最优的减振效果，例如图3 (b)和(e)中的RMSP 降幅达到了86.18%and77.00%，这两个值比Set4相应的降幅稍大。最后，以综合最优的优化布置Set4也能取得很好的控制效果，其RMSP 降幅达到了85.63%和71.41%。这些结论与表2中的结论是一致的。

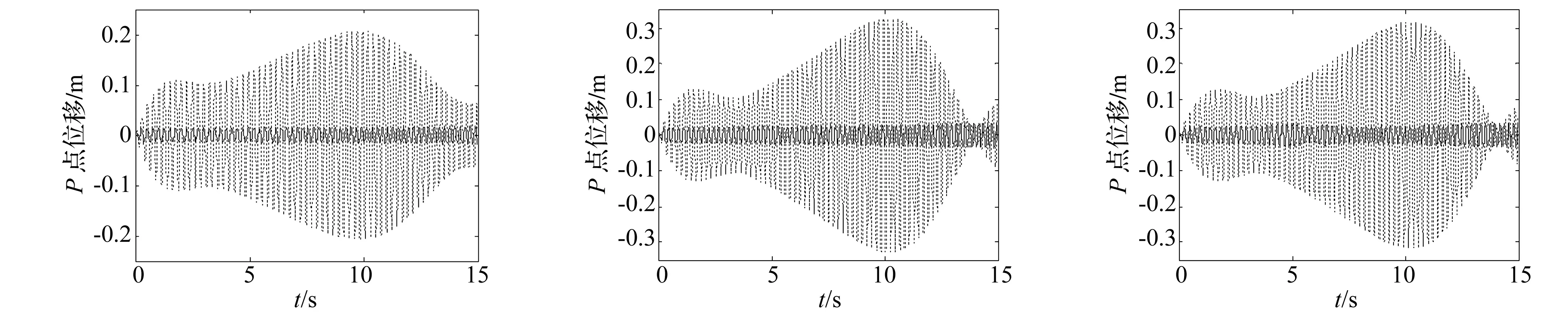
除了上述的分析中采用的频率快扫频，随机激励也是常用的激振载荷。下面采用带宽为2～50 Hz的随机激励，为保证可比性，Set0、1、2和4中的载荷保持相同，有控、无控的响应对比如图4所示。同样的，Set0的减振效果作为对照基准，其RMSP降幅为82.78%，如图4(a)所示。最为显著的是，Set4的RMSP降幅高达89.12%，这个降幅甚至超过了Set0工况。Set1的减振幅度是较高的，这主要是因为第一模态响应在总响应中占比较高，而第二阶响应相对的占比较小，所以Set2的降幅稍小些，如图4(b)、(c)所示。

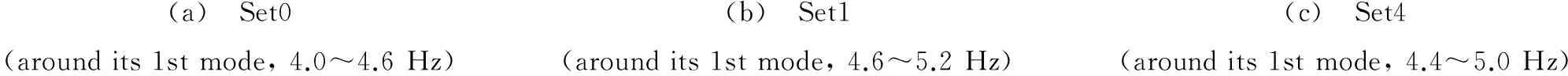
(a) Set0(aroundits1stmode,4.0～4.6Hz)(b) Set1(aroundits1stmode,4.6～5.2Hz)(c) Set4(aroundits1stmode,4.4～5.0Hz)

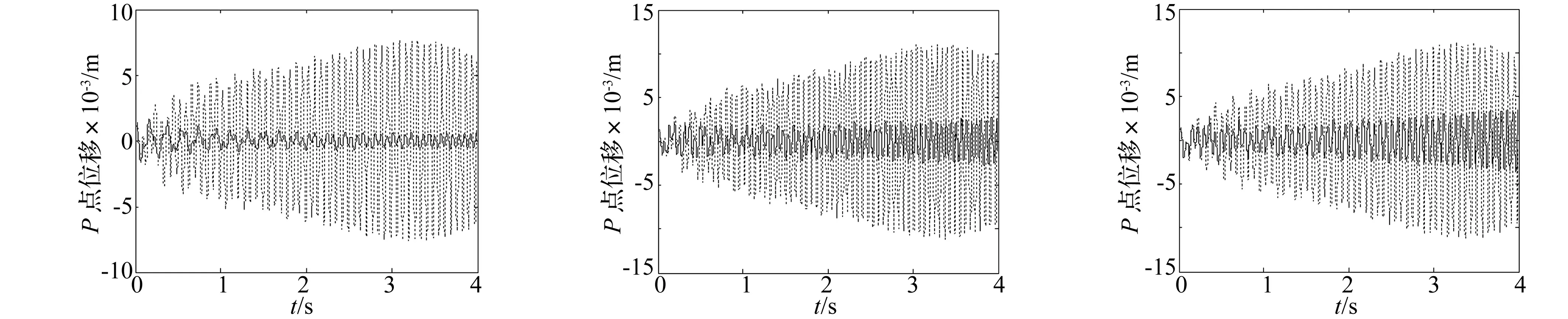
(d) Set0(aroundits2ndmode,13.7～14.5Hz)(e) Set2(aroundits2ndmode,16.2～17.0Hz)(f) Set4(aroundits2ndmode,14.2～15.0Hz)图3 简谐激励下的时域响应.(点线,无控E=0;实线,semi-modal控制,Eb=1kV/mm)Fig.3TimeresponsesofpointPoftheERsandwichplateundersinusoidalexcitation.(pointline,uncontrolledE=0;realline,semi-modalcontrolledEb=1kV/mm)

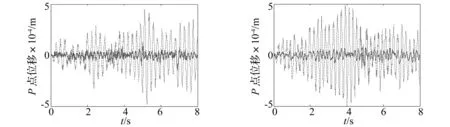
(a) Set0(random2～50Hz)(b) Set1(random2～50Hz)

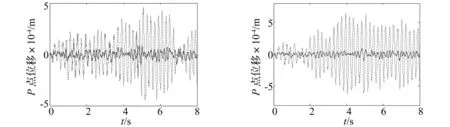
(c) Set2(random2～50Hz)(d) Set4(random2～50Hz)图4 随机激励下的时域响应(点线,无控E=0;实线,semi-modal控制,Eb=2kV/mm)Fig.4TimeresponsesoftheERsandwichplateunderrandomexcitation(pointline,uncontrolledE=0;realline,semi-modalcontrolledEb=2kV/mm)

5 结 论

关注了电流变夹层板结构的半主动振动控制和拓扑优化问题。采用有限元方法建模和分析了结构的模态频率和损耗因子。基于开关变刚度控制策略，设计了一种适用于ER夹层系统的变刚度控制算法。另外，通过粒子群优化算法得到了分别关于单阶、综合模态频率变化率最大的优化构形。最后，采用变刚度控制的等效阻尼和变刚度控制的时域响应对比，对优化构形进行了数值检验。下面是总结出的几个结论：

(1) 变刚度模态控制能适应多种激励工况，取得较好的振动控制效果，当系统呈现模态振动时，控制算法退化成开关变刚度控制，控制效果更为显著。

(2) 在相同材料适用率条件下的多种构形中，针对单阶模态的拓扑优化构形，能取得该阶模态上最优的变刚度控制效果。

(3) 采用综合模态频率变化率的优化布置更能适应复杂激振工况，特别是有带宽的噪声激励时，如图4(d)所示。

[1] CHOI S B, PARK Y K. Active vibration control of cantilevered beam containing an electro-rheological fluid[J]. Sound Vib, 1994 172: 428-32.

[2] YALCINTAS M, COULTER J P. Electrorheological material based adaptive beams subjected to various boundary conditions[J]. Intell. Mater. Syst. Struct,1995,6: 700-717.

[3] 孟光, 鲁宏权, 任兴民. 电流变液夹层板结构动态特性及振动控制的实验研究[J].航空学报1998,19(4):456-461. MENG Guang, LU Hongquan, REN Xingmin. Experiment study on the dynamic characters and vibration control of a sandwich plate with electro-rheological fluid[J]. Acta Aeronaut et Astronautica Sinica, 1998, 19(4):456-461.

[4] 任建亭,吴克恭,闫云聚,等. 电流变液夹层梁滑模振动控制的研究[J].机械强度,2002,24(2):180-184. REN Jianting, WU Kegong, YAN Yunju, et al. Active vibration control of an electrorheological sandwich beam using sliding control method[J]. Journal of Mechanical Strength, 2002, 24(2):180-184.

[5] YEH J Y, CHEN L W. Finite element dynamic analysis of orthotropic sandwich plates with an electrorheological fluid core layer[J]. Composite Structures, 2007, 65: 251.

[6] RAHIMINASABA J, REZAEEPAZHAND J. Effect of boundary conditions on transient response of sandwich plates with electrorheological fluid core[J]. Key Engineering Materials, 2011, 462/463: 372-377.

[7] ELBEHEIRY E. Suboptimal bilinear control methods applied to suppressing car vibrations [J]. Journal of Vibration and Control, 2000, 7(2):279-306.

[8] MEI Xue, LIN Jinguo, XIA Liangzheng. Synergetic pattern recognition based on particle swarm optimization algorithm[C]// In Control Conference, CCC 2008: 505-508.

[9] YOSHIDA H, KAWATA K, FUKUYAMA Y, et al. A particle swarm optimization for reactive power and voltage control considering voltage stability[C]// International Conference on Intelligent System Application to Power System, 1999: 117-121.

[10] GHOLIZADEH S.Layout optimization of truss structures by hybridizing cellular automata and particle swarm optimization[J]. Computers and Structures, 2013,125: 86-99.

[11] ZHAO Fengqiang, LI Guangqiang, YANG Chao, et al. A human computer cooperative particle swarm optimization based immune algorithm for layout design[J]. Neuro Computing, 2014,132: 68-78.

[12] KOBORI T．Dynamics loading test of real scale steel frame with active variable stiffness device[J]．Journal of Structural Engineering,1991,37:317-328.

[13] RATNAWEERA A, HALGAMUGA S K, WATSON H C. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3):240-255.

[14] DON D L, COULTER J P. An analytical and experimental investigation of electrorheological material based adaptive beam structures[J]. Intell. Mater. Syst. Struct, 1995, 6: 846-853.

Topological optimization and vibration control for an ER sandwich plate

CHEN Chunqiang, CHEN Qian

(State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

The semi-active variable stiffness control algorithm for an electrorheological (ER) sandwich plate was designed and the topology optimization was performed for this sandwich structure. Firstly, the dynamic model for the ER sandwich plate was built. The modal control algorithm for this ER plate was developed based on the on-off control strategy. Then, the modal frequency rates for a single mode and multi-mode of the ER sandwith structure, respectively were taken as the optimization objectives, the ER structure was optimized topologically with the particle swarm optimization (PSO) method. The corresponding topological configuration of the ER structure under the contraint of a certain amount of material used were obtained. At last, the equivalent damping ratio of variable stiffness control and the time-domain responses of the ER structure under multi-excitation were adopted to validate the topological optimization results for the ER sandwich plate. Numerical examples showed that the topological optimization results are correct and the variable stiffness control method is effective.

electrorheological(ER) sandwich plate; modal control algorithm; modal frequency rate; particle swarm optimization (PSO); topology optimization; equivalent damping ratio

中央高校基本科研业务费专项资金；江苏高校优势学科建设工程资助

2015-05-05 修改稿收到日期：2015-11-20

陈春强 男，博士生，1987年4月生

陈前 男，教授，博士生导师，1951年11月生 E-mail：Q.chen@nuaa.edu.cn

O328;TP273

A

10.13465/j.cnki.jvs.2016.21.021