基于临界特征值的MDL信源数欠估计分析方法
2016-12-15李一博靳世久曾周末
杜 非, 李一博, 靳世久, 曾周末
(天津大学 精密测试技术及仪器国家重点实验室,天津 300072)
基于临界特征值的MDL信源数欠估计分析方法
杜 非, 李一博, 靳世久, 曾周末
(天津大学 精密测试技术及仪器国家重点实验室,天津 300072)
针对最小描述长度准则下的信源数欠估计问题,提出了一种基于临界特征值的欠估计分析方法,通过对信源数估计算法进行分析,给出了临界特征值的求解表达式及唯一性证明。相比现有方法,临界特征值方法可对不同漏检数下的欠估计边界进行预测,并评估阵列参数对信源数估计性能的影响。为解决大漏检数下的临界特征值的求解复杂问题,提出了一种近似方法,分析了近似误差的影响因素。仿真数值实验结果表明,临界特征值方法可准确描述算法在不同漏检数下的欠估计边界,为基于信息论准则的信源数估计算法提供了一种新的具有普适性的分析手段。
MDL准则;信源数估计;欠估计;阵列信号处理
阵列信号处理技术广泛应用于雷达、通信、声纳、无损检测等多个领域。信源数估计是阵列信号处理中的重要问题,估计结果的准确度及倾向性对如空间谱估计、到达角定向等后继算法的性能和策略具有重要影响[1]。
信源数估计方法的原理包括假设检验、信息论、特征向量正交性等[2]。其中以Akaike信息论准则(Akaike Information Criterion,AIC)[3]和最小描述长度准则(Minimum Description Length Criterion,MDL)[4-5]为代表的信息论方法由于其符合最大似然估计理论,计算相对简单,在工程实践中得到广泛应用。WAX等[6]指出尽管AIC准则在小快拍数下具有相对更好的性能,但无法实现一致估计,呈渐近的过估计趋势;而MDL信源数估计算法在快拍数较大时具有估计一致性,在对快拍数要求不高的场合下具有更好的性能优势。然而,在信号具有相似的子空间时,MDL信源数估计算法容易发生欠估计现象,导致信号源的漏检,是制约其应用的主要问题。研究MDL信源数估计算法的欠估计条件,对改善其在低信噪比等恶劣条件下的性能,以及后继算法的研究具有重要的指导价值。
现有方法多基于概率理论对MDL信源数估计算法的欠估计现象进行研究。ZHANG等[7]指出相关矩阵特征值与噪声功率的比值,以及采样快拍数会影响MDL信源数估计算法的欠估计条件,但只给出了定性的结果。KRITCHMAN等[8]给出了基于相关矩阵特征值描述的欠估计条件的近似表达式, NADLER等[9]后继又提出了算法正确检测概率不低于0.5的近似条件。LU等[10]得到了基于信号特征值与噪声特征值均值之比表示的算法欠估计条件,并分析了算法的欠估计边界,但并未对算法性能的影响因素进行讨论。此外,现有方法均主要针对算法的欠估计条件进行研究,而对于算法的欠估计程度未做深入探讨。
本文提出了一种基于临界特征值的MDL信源数估计算法的欠估计分析方法,给出了临界特征值的唯一性证明,分析了快拍数和阵元数量对算法性能的影响,并基于仿真实验验证了本文方法的有效性。相比现有方法,本文提出的方法能够准确描述不同漏检数下算法的欠估计边界,可评估特定参数下信噪比对信源数估计结果的影响,具有较高的应用价值。由于大多数信息论方法与MDL准则具有相似的表达形式,因此本文提出的方法具有良好的普适性,可用于如HQ[11], WIC[12], FDC[10]等算法的性能分析和评估。
1 阵列信号模型
K个远场窄带信号源传播到具有N(N>K)个阵元的线阵列的信号模型可描述为
x(t)=A(θ)s(t)+n(t)
(1)
式中:x(t)为各阵元所观测到的时域信号,A(θ)为N×K的阵列流形矢量矩阵
A(θ)=[a(θ1),a(θ2)…a(θK)]
(2)
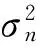
R=E{x(t)xH(t)}=
(3)
记无噪声矩阵=A(θ)RSAH(θ)的特征值为λi,并降序排列有
(4)
式中:
λ1≥λ2≥…≥λK
(5)
则R的特征值为
(6)
并且
(7)
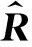
(8)
相应的特征值记为
(9)
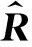
2 临界特征值理论
2.1 MDL信源数估计算法的欠估计条件
独立高斯条件下,基于理想相关矩阵R的特征值表示的MDL信源数估计算法的计算方法为
MDL(k)=-L(k)+y(k)=
(10)
式中:T为信号采样的快拍数,L(k)为最大似然项,y(k)为惩罚项,则估计信源数K′为
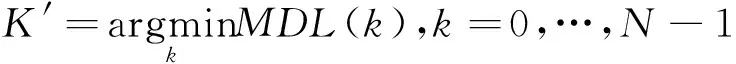
(11)
理想情况下,当快拍数T趋于无穷大时,算法将得到信源数量的真实估计。然而在实际应用中,快拍数T过大将对算法的实时性产生影响,阵元数量亦受到应用条件的制约。因此,需对算法的欠估计发生条件进行研究,并分析快拍数、阵元数量和信噪比等参数对算法性能的影响。
假设真实信源数量为K,算法估计得到的信源数量为K′,当K′≤K-1时,即存在欠估计的情况,有
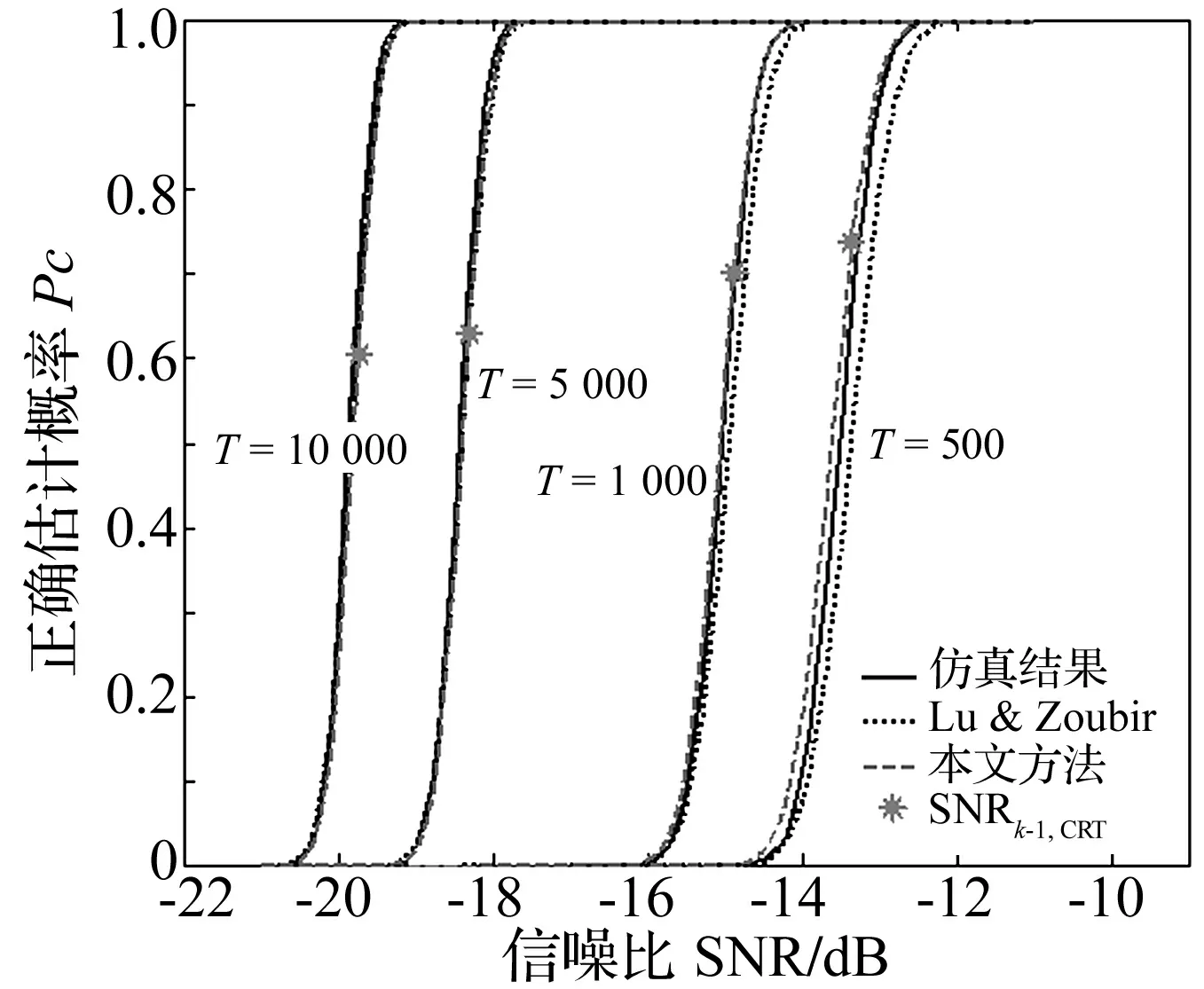
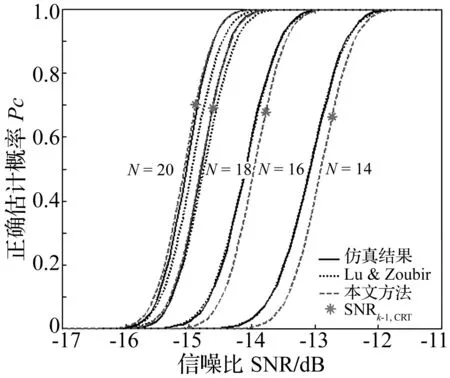
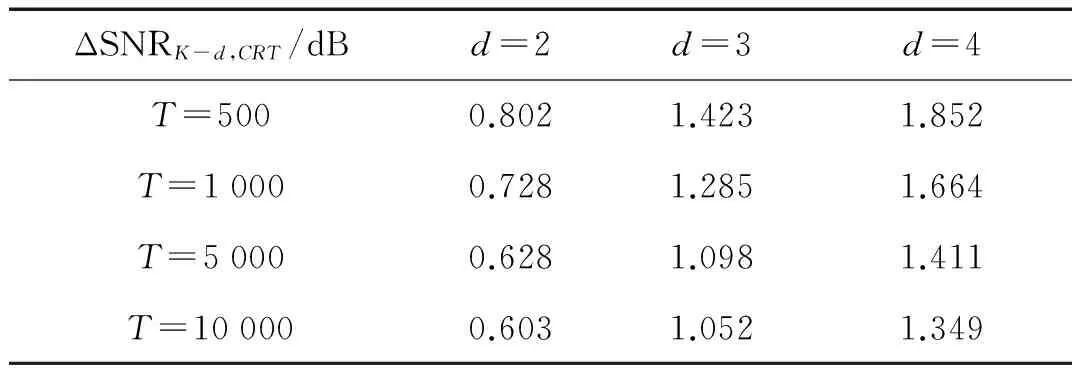
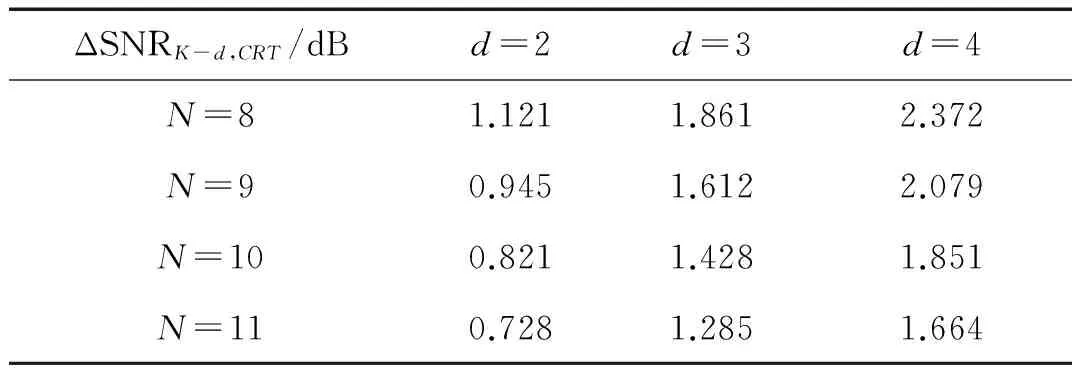
MDL(K-1) (12) 将式(10)代入式(12),得到 (13) 化简有 (14) 为进一步简化,定义 (15) 则式(14)可改写为 (16) 式(16)即为算法发生信源数欠估计的必要条件。为进一步分析,左式对bK求导有 (17) 2.2 不同漏检数下算法的欠估计条件 多信源条件下,漏检数可有效描述算法的欠估计程度。考虑估计信源数K′≤K-d的情况,d为最小漏检数,有 MDL(K-d) (18) 将式(10)代入式(18),得到 (19) 与式(15)类似,假设 (20) 有 (21) 式(21)即为漏检数大于等于d的必要条件。当不等式取等时,解得的bK-d+1即为最小漏检数d所对应的临界特征值bK-d+1,CRT。将bK-d+2,bK-d+3…bK视为常数,式(21)左侧对bK-d+1求导有 (22) 因为bK-d+1>bi,i≥K-d+2,所以有 (23) 式(22)在bK-d+1的取值区间内大于零,因此式(21)的左式随bK-d+1单调递增,可求出其唯一解bK-d+1,CRT。临界特征值bK-d+1,CRT除与快拍数T,信源数量K及阵元数量N有关外,还与bK-d+2…bK等d-1个特征值与噪声功率之比有关。临界特征值bK-d+1,CRT越小,算法对噪声的抗性越好。 2.3 欠估计概率分析 (24) 即不发生相位反转的条件下服从以下正态分布: (26) 根据式(16)中左式的单调递增特性,其成立的概率等价于 (27) 临界特征值bK,CRT仅与阵列参数有关,因此可根据正态分布累积分布函数直接求得信源数欠估计概率随信噪比的变化。同理,式(21)成立的概率为 (28) 值得注意的是,临界特征值bK-d+1,CRT不仅取决于阵列参数,还和bK-d+2…bK之和有关。为便于计算,本文中假设仅考虑信噪比对bK-d+2…bK期望值的影响,忽略其随机误差。根据式(26)可以得知,在快拍数较大的情况下,这一假设将具有较好的近似性。 上文中提到快拍数T,阵元数量N和信源数量K等参数对MDL信源数估计算法的性能存在明显影响,本节将基于临界特征值理论对算法性能的影响因素进行研究。 3.1 最小漏检数为1时的算法性能分析 首先对估计信源数K′≤K-1,即算法存在欠估计的情况进行研究。对于快拍数量T,根据式(16)可知,由于lnT/T项的存在,当快拍数T增大时临界特征值bK,CRT将逐渐变小,算法性能得到改善。当快拍数T无 限大时, 临界特征值bK,CRT等于1。由于bK>1,此时算法将不存在欠估计现象,可正确估计信号源的真实数量。然而,实际应用中快拍数不可能无限大,为控制算法发生欠估计的概率,可基于临界特征值方法计算得到所需的最小采样快拍数。 对于信源数量K和阵元数量N,从式(16)中可以看出,当其他参数保持不变,N-K为相同值时,所求得的临界特征值bK,CRT理应相同,直观上两者对算法性能应具有相反影响。然而,阵元数量N与相关矩阵R的迹呈线性正相关,N增加时R的特征值也会增加,因此在分析阵元数量N的影响时需对临界特征值bK,CRT进行归一化处理。信源数量K与R的迹同样具有正相关性,但并非线性相关,具体与阵元数量N和信噪比有关,无法简单的对其进行归一化处理;并且在实际应用中,信源数量K的增加可能使信号具有相近的子空间,使相关矩阵特征值发生变化,因此本文仅针对快拍数量T和阵元数量N对算法性能的影响进行讨论。图1为不同信源数量K下,快拍数T和阵元数量N对归一化临界特征值的影响,经过归一化处理的bK,CRT随着快拍数T和阵元数量N的增加而降低,预示着算法性能的提高。随着快拍数T的增加,提高快拍数所带来的边际效益有所下降,这是由于lnT/T项的减小速率变缓导致的。 图1 归一化临界特征值bK,CRT随快拍数和阵元数量的变化Fig.1 The variation of normalized bK,CRT with the number of snapshots and array elements 3.2 多漏检数下的算法性能分析 当最小漏检数d>1时,由式(21)可以得知,临界特征值bK-d+1,CRT除受到快拍数T,阵元数量N和信源数量K的影响以外,还与bK-d+2…bK等d-1个特征值与噪声功率的比值有关。为表述方便,在对临界特征值bK-d+1,CRT进行分析时,假设bK-d+2…bK的取值分别为其对应的临界特征值bK-d+2,CRT…bK,CRT,在这一假设下研究各项参数对算法性能的影响。 图2为最小漏检数d=2时,不同信源数量K下归一化的临界特征值bK-d+1,CRT随快拍数T和阵元数量N的变化。与最小漏检数为1的情况类似,归一化的bK-1,CRT随着快拍数T和阵元数量N的增加而降低,算法性能相应提高。当最小漏检数d为其他值时,对应的归一化临界特征值bK-d+1,CRT同样具有类似规律,本文中不再逐一列出。 图3为信源数量K=6时,不同快拍数T以及阵元数量N下归一化临界特征值随最小漏检数d的变化,可以看到归一化的bK-d+1,CRT随d的增加而上升,符合bi的降序排列规律。当快拍数T和阵元数量N增加时,归一化的临界特征值bK-d+1,CRT具有更低的取值,与上文结论相符。值得注意的是,随着上述参数的增加,曲线的斜率将变得平缓,表明漏检数d对bK-d+1,CRT的影响变弱。 图2 归一化临界特征值bK-1,CRT随快拍数和阵元数量的变化Fig.2 The variation of normalized bK-1,CRT with the number of snapshots and array elements 图3 不同快拍数及阵元数下归一化的bK-d+1,CRT随d的变化Fig.3 The variation of normalized bK-d+1,CRTwith d under different numbers of snapshots and array elements (29) 由于临界特征值在评价算法性能时不够直观,将式(29)代入式(16)和式(21)中可求得信源估计数小于K-d时的信噪比临界值,记为SNRK-d,CRT,可作为评价算法性能的有效指标。PC表示信源数的正确估计概率,E(K′)表示信源数估计结果的期望值,所有的仿真结果均基于5 000次的蒙特卡洛模拟获得。 4.1 最小漏检数为1的实验结果 图4 不同快拍数下PC随SNR的变化Fig.4 The variation of PC with SNR for different values of snapshots 图5 不同阵元数量下PC随SNR的变化Fig.5 The variation of PC with SNR for different numbers of array elements 图5为不同阵元数N下算法的信源数正确估计概率PC随信噪比SNR的变化曲线,实验参数为θ={-3°, 3°},K=2,N=[14,16,18,20],T=1 000。本文所提出的基于临界特征值的分析方法和参照方法均能有效预测算法的欠估计边界。本文方法与参照方法在不同的阵元数量下的预测精度互有优劣,与两者采用的样本特征值分布模型有关。与图4相似,随着阵元数量N的增加,欠估计边界所对应的信噪比呈下降趋势,表明算法具有更好的性能,与上文分析相符。 4.2 多漏检数的实验结果 为研究算法在不同漏检数下信源数欠估计程度随信噪比的变化,本文采用信源数估计结果的期望值E(K′)代替正确估计概率PC对算法性能进行分析,可同时描述不同漏检数下算法的欠估计边界。由于式(21)两侧均包含bi项,其取值与信噪比相关,在计算bK-d+1,CRT和SNRK-d,CRT时需将式(29)代入式(21)两侧进行复杂求解。为简化计算,假设式(21)右侧的bi近似等于其所对应的临界特征值bi,CRT,则可通过简单递推计算得到临界特征值bK-d+1,CRT。记基于该近似方法计算得到的信噪比临界值为SNRK-d,CRT,C,其与精确求解所得到的临界信噪比SNRK-d,CRT之间的差值记为 ΔSNRK-d,CRT=SNRK-d,CRT,C-SNRK-d,CRT (30) ΔSNRK-d,CRT越小,近似所产生的误差就越小。 仿真实验中,本文分别基于所提出的精确方法及近似方法对算法的信源数估计结果进行预测。图6为不同快拍数T下估计信源数期望E(K′)随信噪比SNR的变化,实验参数为θ={-7°,-4°,0°,4°,7°},K=5,N=11,T=[500,1 000,5 000,10 000]。可以看到本文所提出的方法能够准确预测不同漏检数下算法的信源数欠估计边界,验证了本文方法的有效性。近似方法同样能够反映算法的欠估计程度随信噪比的变化,但在d>1时与仿真结果存在一定的偏移误差。基于图6的实验参数,表1为不同最小漏检数d和快拍数T下临界信噪比近似误差ΔSNRK-d,CRT的值。该值随着最小漏检数d的增加而增加,这是由于bi与bi,CRT之间的误差累积所致。随着快拍数T的增加,同一最小漏检数d下的ΔSNRK-d,CRT呈变小趋势,与图3所描述的规律相符,验证了临界特征值分析方法的有效性。 图6 不同快拍数下E(K′)随SNR的变化Fig.6 The variation of E(K′) with SNR for different values of snapshots 图7为不同阵元数量N下估计信源数期望E(K′)随信噪比SNR的变化曲线,实验参数为θ={-7°,-4°,0°,4°,7°},K=5,N=[8,9,10,11],T=1 000。与图6类似,本文提出的方法能够准确预测不同漏检数下算法的信源数欠估计边界,近似方法在最小漏检数d>1时与仿真结果之间存在偏移误差。表2中列出了基于图7实验参数,在不同最小漏检数d和阵元数量N下ΔSNRK-d,CRT的值。该值同样随着最小漏检数d的增加而变大,同一d值下近似误差ΔSNRK-d,CRT随阵元数的增加逐渐变小,与图3所描述的规律相符。因此,在阵元数量N和快拍数T较大时,对于较小漏检数,可用近似方法对算法性能进行分析以简化计算;其他条件下则需对临界特征值bK-d+1,CRT进行精确求解以准确预测算法的信源数估计结果。 图7 不同阵元数量下E(K′)随SNR的变化Fig.6 The variation of E(K′) with SNR for different numbers of array elements ΔSNRK-d,CRT/dBd=2d=3d=4T=5000.8021.4231.852T=10000.7281.2851.664T=50000.6281.0981.411T=100000.6031.0521.349 表2 ΔSNRK-d,CRT随最小漏检数d和阵元数量N的变化 本文通过对MDL准则下的信源数估计算法进行研究,提出了一种基于临界特征值的信源数欠估计分析方法,指出相关矩阵的特征值与噪声功率之比是描述欠估计条件的有效指标,并给出了临界特征值的求解方法及唯一性证明。结合随机矩阵理论,该方法可准确预测不同漏检数下算法的欠估计边界,并分析阵列参数对算法性能的影响。为降低大漏检数下临界特征值的求解复杂度,提出了一种基于递推求解的近似分析方法,在快拍数和阵元数量较大时对于小漏检数欠估计边界具有较好的近似预测效果。仿真实验与理论分析结果相符,验证了临界特征值方法的有效性和准确性。该方法可应用于多种基于信息论的信源数估计算法,具有广泛的适用性,为相关算法的研究和阵列设计提供了参考依据。 [1] KRIM H, VIBERG M. Two decades of array signal processing research: The parametric approach [J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94. [2] AOUADA S, ZOUBIR A M, SEE C M S. A comparative study on source number detection [C]// IEEE. Signal Processing and Its Applications, 2003. Proceedings. Seventh International Symposium on. USA: IEEE, 2003:173-176. [3] AKAIKE H. Information theory and an extension of the maximum likelihood principle [C]// Petrov B N, Csaki F. 2nd Int. Symp. Inform. Theory, suppl. Problems of Control and Inform. Theory. Budapest: Akadémiai Kiadó,1973: 267-281. [4] RISSANEN J. Modeling by shortest data description [J]. Automatica, 1978, 14(5): 465-471. [5] SCHWARZ G. Estimating the dimension of a model [J]. Annals of Statistics, 1978, 6(2): 461-464. [6] WAX M, KAILATH T. Detection of signals by information theoretic criteria [J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(2): 387-392. [7] ZHANG Q T, WONG K M, YIP P C, et al. Statistical analysis of the performance of information theoretic criteria in the detection of the number of signals in array processing [J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(10): 1557-1567. [8] KRITCHMAN S, NADLER B. Non-parametric detection of the number of signals: hypothesis testing and random matrix theory [J]. IEEE Transactions on Signal Processing, 2009, 57(10): 3930-3941. [9] NADLER B. Nonparametric detection of signals by information theoretic criteria: performance analysis and an improved estimator [J]. IEEE Transactions on Signal Processing, 2010,58(5): 2746-2756. [10] LU Z, ZOUBIR A M. Flexible detection criterion for source enumeration in array processing [J]. IEEE Transactions on Signal Processing, 2013, 61(6):1303-1314. [11] HANNAN E J, QUINN B G. The determination of the order of an autoregression [J]. Julia Campos Fernández, 1979, 41(2): 190-195. [12] WU T J, SEPULVEDA A. The weighted average information criterion for order selection in time series and regression models [J]. Statistics & Probability Letters, 1998, 39(1): 1-10. [13] NADAKUDITI R R, EDELMAN A. Sample eigenvalue based detection of high-dimensional signals in white noise using relatively few samples[J]. IEEE Transactions on Signal Processing, 2008, 56(7): 2625-2638. Underestimation analysis for MDL source enumeration based on critical eigenvalues DU Fei, LI Yibo, JIN Shijiu, ZENG Zhoumo (State Key Laboratory of Precision Measurement Technology and Instruments, Tianjin University, Tianjin 300072, China) A method based on critical eigenvalues was proposed to evaluate the underestimation problem of source enumeration under the minimum description length (MDL) criterion. The uniqueness of critical eigenvalues was proved and their solution expression was presented with the analysis of the enumeration algorithm. It was shown that the critical eigenvalue method can predict the boundary of underestimation for different numbers of undetected sources and evaluate the influences of array parameters on the performance of source enumeration, compared with the existing methods. An approximation method was proposed to reduce the calculation complexity of solving critical eigenvalues under the condition of large numbers of undetected sources and the factors affecting the approximation errors were also analyzed. Simulation results indicated that the critical eigenvalue method can exactly describe the boundary of underestimation of source enumeration. The results provided a new analysis tool for other source enumeration methods based on information criteria. minimum description length (MDL) criterion; source enumeration; underestimation; array signal processing 国家自然科学基金青年科学基金(61304244;61201039);国家重点实验室成果培育项目;天津市自然科学基金(13JCYBJC18000) 2015-05-05 修改稿收到日期:2015-10-28 杜非 男,博士生,1986年生 靳世久 男,教授,博士生导师,1946年生 TH76;TN95 A 10.13465/j.cnki.jvs.2016.21.017
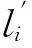

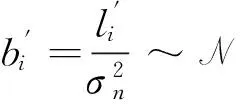
3 基于临界特征值的算法性能分析



4 数值仿真实验
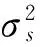
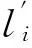
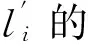


5 结 论
