齿轮传动系统中行星轮断齿故障特征分析

王 鑫， 徐玉秀， 武宝林

(1.天津工业大学 机械工程学院,天津 300387； 2.现代机电装备技术重点实验室,天津 300387)



齿轮传动系统中行星轮断齿故障特征分析

王 鑫1,2， 徐玉秀1,2， 武宝林1

(1.天津工业大学 机械工程学院,天津 300387； 2.现代机电装备技术重点实验室,天津 300387)

为识别齿轮传动系统中行星轮断齿故障特征及其连带的故障本质特征，建立了2级定轴齿轮+1级行星轮的风电齿轮传动系统量纲-动力学方程。对比研究正常与行星轮断齿故障状态下系统随激励频率变化的故障特性。通过研究发现了行星轮断齿故障引发的脱齿-碰撞现象，断齿故障特征及连带故障特征。依据仿真结果识别出实验信号中无法确定的由行星轮断齿故障引起的连带故障信号，诊断出故障特征表现微弱的行星轮断齿故障。

行星齿轮传动；非线性动力学系统；分岔；断齿故障；连带故障特征

在风电齿轮传动系统的实验信号中发现，定轴齿轮的振动冲击较大，行星轮的振动相对很小，故其信号显得微弱。由于定轴齿轮与行星轮因多间隙而产生非线性动力学耦合，行星轮啮合频率处边频较少，而非啮合频率处出现大量边频[1]。对此，研究行星轮故障的微弱特征及这些边频信号是否为行星轮故障引起的连带信号，对行星轮故障诊断具有重要意义。

对于行星轮微弱故障的识别，梁晓玉等[2]基于混沌理论对行星齿轮传动系统单一及耦合故障进行分类与识别。MGHANTY[3]从实验角度研究了行星轮断齿故障的动态信号特性。对于行星轮连带边频的研究，冯志鹏等[4-5]建立了行星齿轮箱故障状态下的振动信号模型，推导分析了行星轮故障振动信号的频谱特征。雷亚国等[6]建立行星齿轮箱的振动信号仿真模型，对比实验及仿真模型在正常及故障状态下的信号，归纳行星齿轮箱局部故障时的振动信号特点。以上研究均从实验信号分析的角度总结行星轮的故障振动特性，没有从振动机理上研究行星轮的故障特性及连带特性。本文应用仿真方法从非线性角度研究行星轮断齿故障下齿轮传动系统的分岔特性及故障机理，应用其频谱特征识别实验信号中的行星轮故障的微弱特性。为行星齿轮传动系统故障诊断提供理论基础。

1 齿轮传动系统扭转动力学模型

本文研究的系统为2级定轴齿轮+1级行星轮组成的风电齿轮传动试验台，如图1所示，其中1级定轴齿轮为输入，行星架为输出，用4个行星轮来分担载荷，行星轮断齿故障程度为40%。利用集中质量法建立系统的扭转动力学模型，该模型不考虑齿轮的横向振动位移，齿轮啮合参数用弹簧和阻尼器进行模拟，建立如图2所示的系统扭转振动模型。

1. 电机；2. 扭矩传感器和编码器；3. 2级定轴齿轮箱；4. 轴承径向负载；5. 1级行星齿轮箱；6. 磁力制动器；图1 风电齿轮传动试验台及故障行星轮Fig.1 The test rig of the wind turbine gear transmission system and fault planetary gear

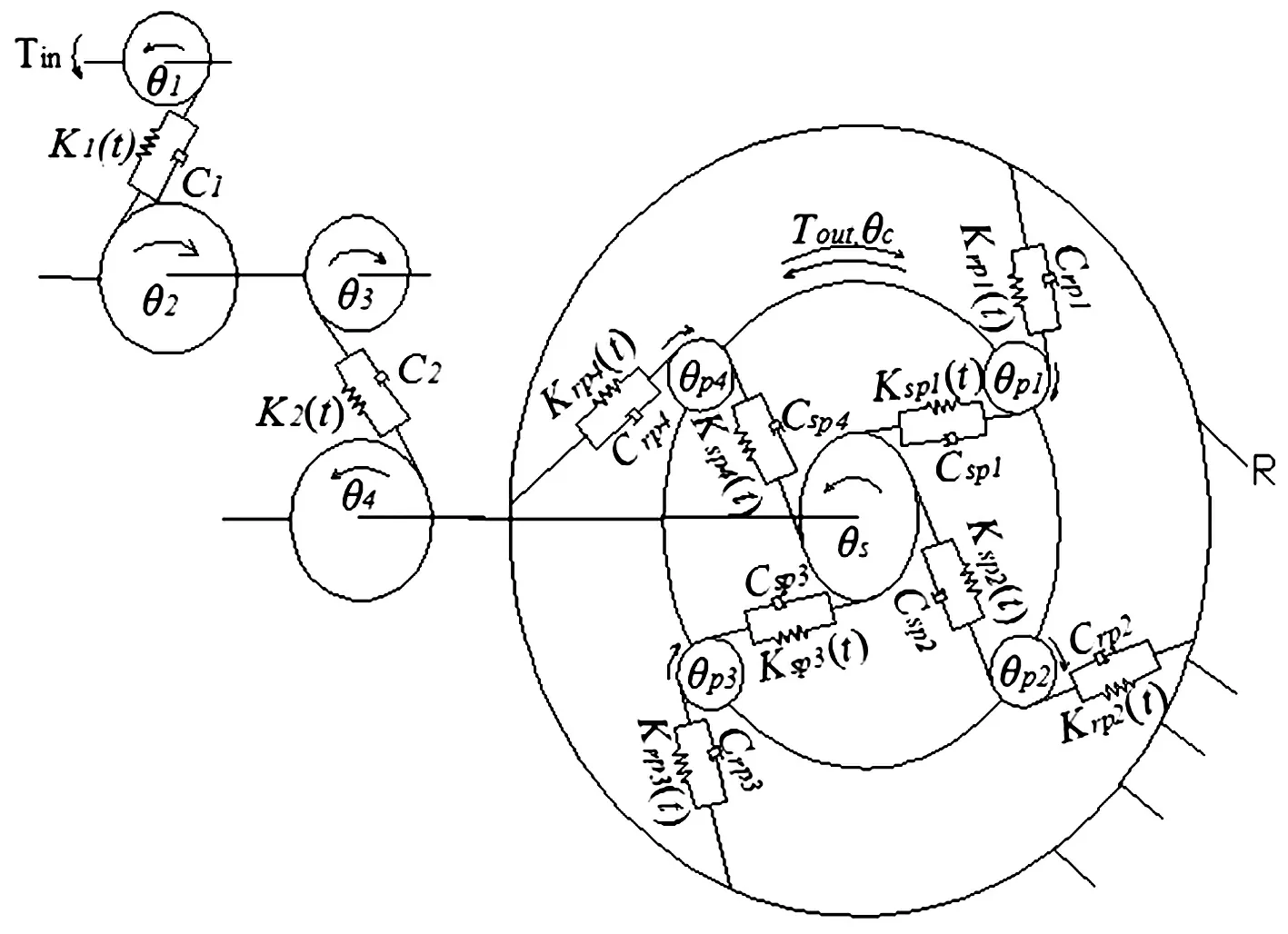
图2 齿轮传动系统扭转振动模型Fig.2 Torsional dynamics model of gear transmission system

图中，θs、θc、θpn、θ1、θ2、θ3、θ4分别为太阳轮、行星架、第n个行星轮(n=1,2,3,4)、直齿轮1、2、3、4的角位移。在本文中约定下标s，c，pn，r，1，2，3，4分别表示太阳轮、行星架、第n个行星轮(n=1,2,3,4)、内齿圈及直齿轮1、2、3、4。rs，rc，rpn，r1，r2，r3，r4分别为各齿轮的基圆半径；Kspn(t)，Krpn(t)，K1(t)，K2(t)为太阳轮与第n个行星轮、内齿轮与第n个行星轮、1级定轴齿轮、2级定轴齿轮的啮合刚度；Cspn，Crpn，C1，C2为太阳轮与第n个行星轮、内齿轮与第n个行星轮、1级定轴齿轮、2级定轴齿轮的阻尼；Tin、Tout为输入扭矩、输出扭矩。

1.1 系统运动微分方程

在考虑齿隙间隙、时变啮合刚度、综合啮合误差的基础上，根据拉格朗日方程建立图1所示系统的运动微分方程[7-8]：

(1)

式中:J23=J2+J3，J4s=J4+Js，其中J1，J2，J3，J4，Js，Jpn，Jc分别为轴上各齿轮的转动惯量；

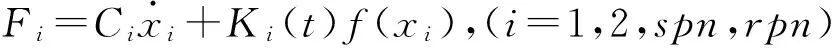
xi为各级齿轮啮合线上的相对位移，(i=1, 2,spn,rpn)，

x1=r1θ1-r2θ2-e1(t)

x2=r3θ3-r4θ4-e2(t),

xspn=rsθs-rpnθpn-rcθc-espn(t)

xrpn=rpnθpn-rcθc-erpn(t)

f(xi)为齿侧间隙非线性函数，(i=1, 2,spn,rpn)，定义为

(2)

式中:bi为齿侧间隙的一半，(i=1, 2,spn,rpn)。

齿轮副的时变啮合刚度Ki(t)可表示为

Ki(t)=Kmi+Kaisin(wmit+φi)

(3)

式中:Kmi为各级齿轮平均啮合刚度，(i=1, 2,spn,rpn)；Kai为啮合刚度变化幅值，(i=1, 2,spn,rpn)；φi为刚度变化幅值的初始相位，(i=1, 2,spn,rpn)；wmi为各级齿轮啮合频率，(i=1, 2,spn,rpn)。

阻尼系数表达式为

(4)

式中:ξ1，ξ2，ξspn，ξrpn分别为各级齿轮副的阻尼比；m1，m2，m3，m4，ms，mpn，mr分别为各齿轮的质量。

齿轮副的综合啮合误差采用啮合函数的一次谐波形式，即

ei(t)=eaisin(wmit+φi)

(5)

式中:eai为各级齿轮综合啮合误差幅值，(i=1，2,spn，rpn)；φi为各级齿轮综合啮合误差初始相位，(i=1, 2,spn,rpn)。

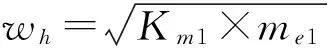
(6)

对方程进行归一化处理，得系统量纲一运动微分方程组：

(7)

式中:me1、me2、me3为齿轮的等效质量，

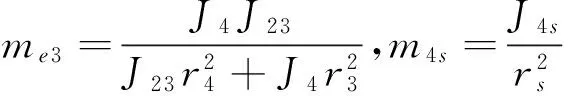
1.2 断齿故障函数

当齿轮存在单齿局部断齿故障时，在其断齿处刚度会减弱，而其他齿处刚度不变。依据GB/T3480—1997渐开线圆柱齿轮承载能力计算方法中平均啮合刚度的计算公式[9]

Kmi=Crh

(8)

式中：Cr是端面内轮齿总刚度的平均值，h为齿宽，取Cr=20 N/(mm·μm)，h=10 mm。

由式(8)可知，齿宽与平均啮合刚度成正比。单齿发生断齿故障时，其齿宽变小，导致单齿平均啮合刚度变小。用aδ(τ)表示断齿故障。a为断齿程度；δ(τ)为幅值为1的周期脉冲函数，周期为齿轮旋转一周的时间，脉冲宽比为1∶N(N为齿轮齿数)。得到量纲一时变啮合刚度故障函数[10]

Ki(τ)=1+εisin(Ωit+φi)-aδ(τ)

(9)

式中:Ωi为量纲一激励频率，Ωi=wmi/wh，(i=1, 2,spn,rpn)；εi为刚度波动系数，εi=Kai/Kmi，(i=1, 2,spn,rpn)。

2 行星轮断齿故障分岔特性

2.1 正常与行星轮断齿故障分岔特性对比

分别计算系统正常与行星轮断齿故障状态下随激励频率的分岔图，其结构参数见表1、2，压力角α=20°，Km1=Km2=3×108N/m，Kmspn=Kmrpn=2×108N/m，Tin=6.5 N·m，Tout=8.5 N·m。下表2中的取值在齿轮的啮合线上相等，故省略下标i。

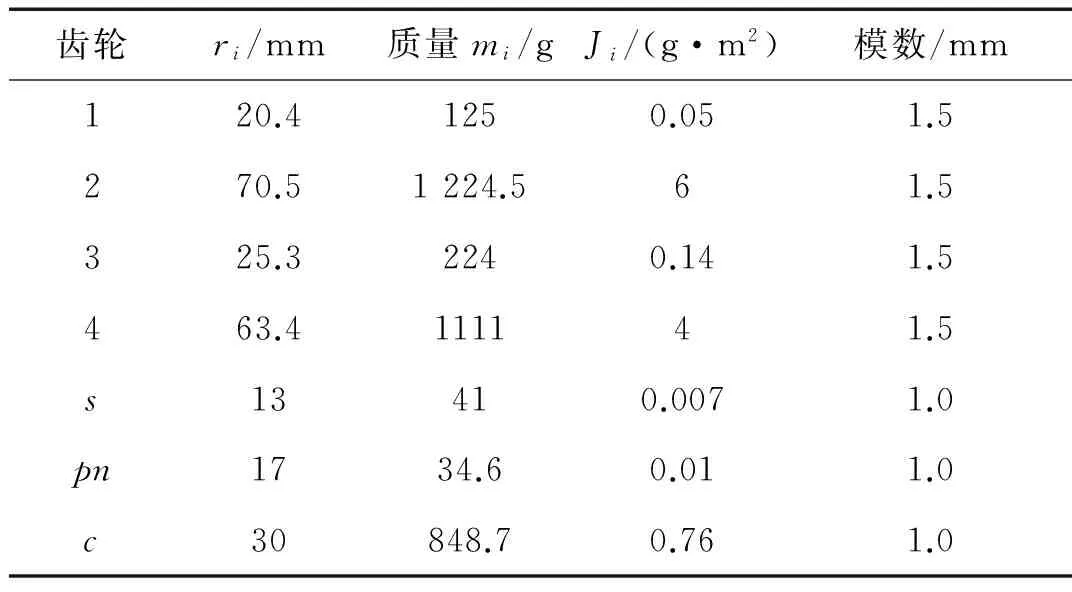
表1 各齿轮的参数

表2 计算参数

采用变步长Runge-Kutta法对非线性微分方程组(7)进行数值求解，得到正常状态下各级齿轮的相对位移随量纲一激励频率变化的分岔图，如图3。

由图3可见，正常状态下系统随激励频率增加振动幅值越来越大。2级定轴齿轮由于同时受1级定轴齿轮与行星齿轮的影响振动幅值最大，如图3(b)；行星齿轮因其均布承载的特性，振动微弱，振动幅值最小，如图3(c)。

假设行星齿轮系统中一个行星轮发生a=0.4的断齿故障，将故障激励函数式(9)代入式(7)计算其分岔图，如图4。

对比图3、4发现，在区间[0,1]出现行星轮断齿故障特征，其中Ω较小时故障特征明显。当激励频率逐渐增大时振动幅值增大，振动状态更为复杂，故障特征减弱，不易辨识。由于太阳轮与2级定轴齿轮同轴，断齿故障在行星齿轮及2级定轴齿轮上表现明显，如图4(b)。1级定轴齿轮相对故障距离较远，故障特性不明显，如图4(a)。由于Ω较小时故障特征明显，而Ω=1时发生共振，下面针对这两个状态对比分析正常及行星轮故障状态下行星轮振动响应的变化。

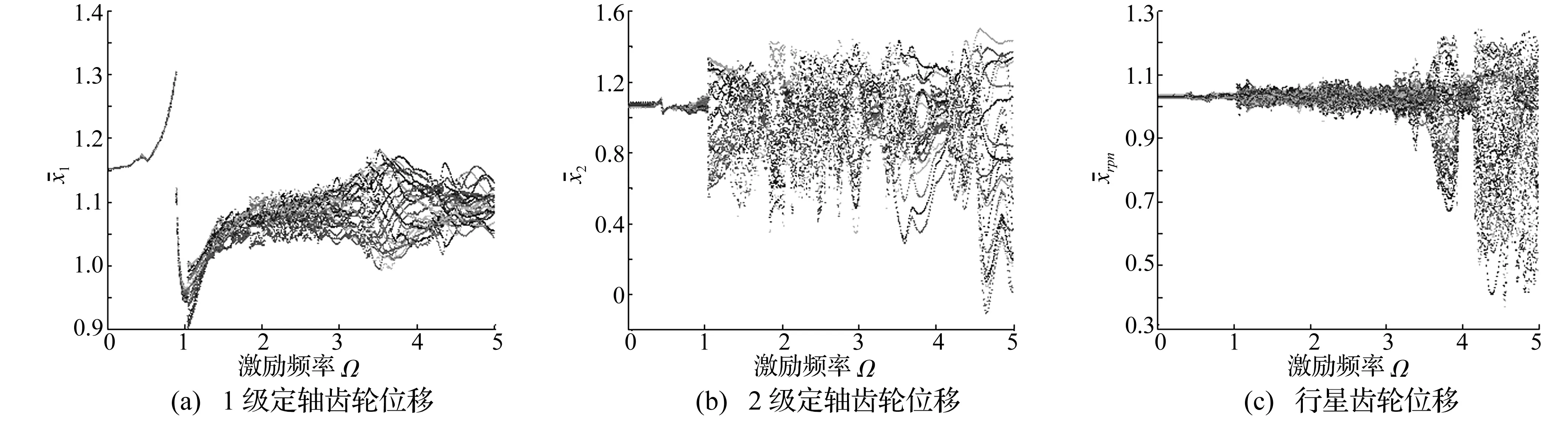
图3 随激励频率变化的分岔图Fig.3 Bifurcation diagram with excitation Frequency

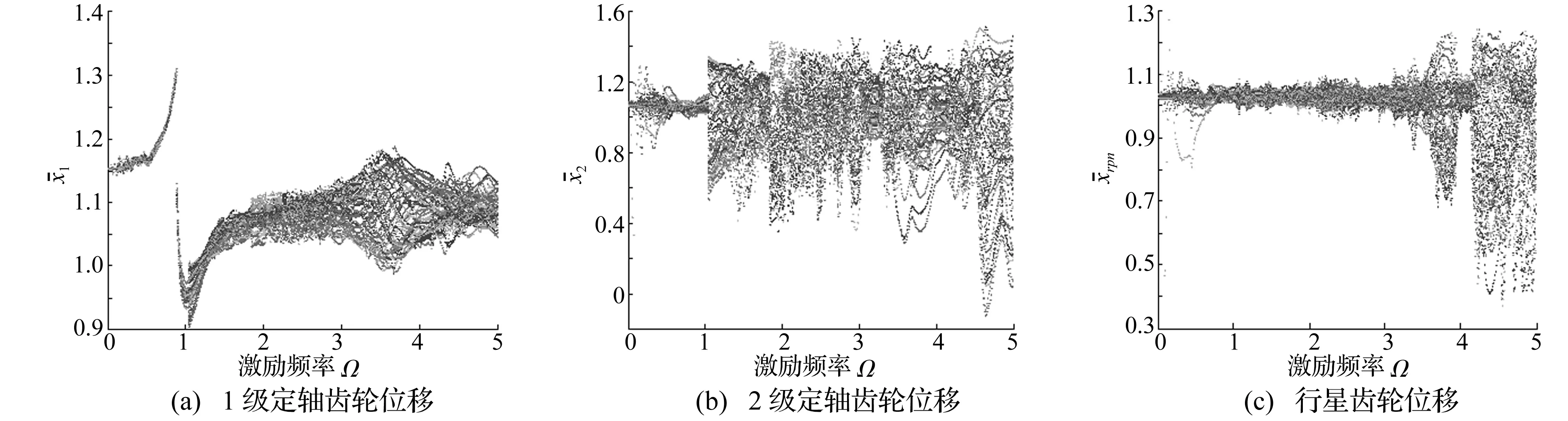
图4 断齿故障下分岔图Fig.4 Bifurcation diagram with chipping fault

2.2 Ω较小时的故障特性

从频谱可以看出，行星轮啮合点处其频谱仅出现行星轮啮合频率(Ωrpn=0.088)及其2倍频，故障发生时在行星轮啮合频率周围出现故障边频。

2.3 Ω=1时的故障特性

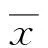
3 实验分析

对图1所示风电齿轮传动试验台进行信号分析。由于实验测得的信号往往含有噪声，可能使频谱图上的有用信息被淹没在噪声背景中。本文采用适合非线性信号的小波包算法进行降噪。通过调节试验台电机转速来改变激励频率。图7为系统故障状态下对应理论分析Ω=0.2及Ω=1时行星轮啮合点处降噪并量纲一化后的频谱图。

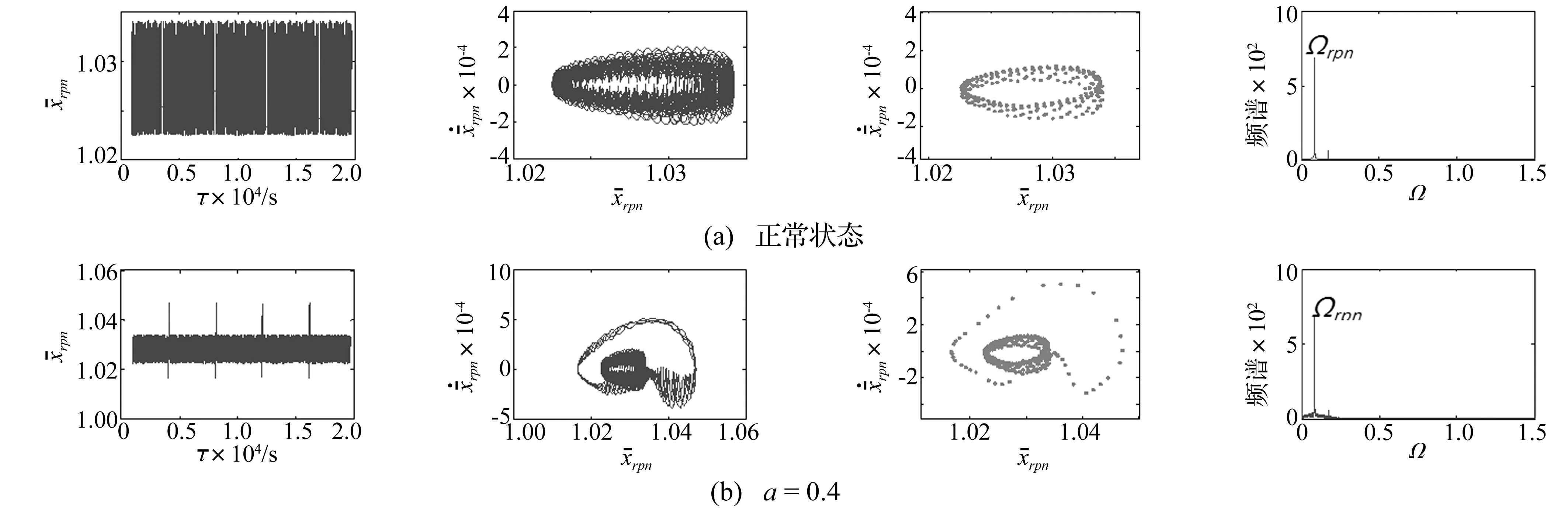
图5 Ω=0.2时正常及故障状态下行星轮振动响应变化Fig.5 The vibration response of planetary gear with normal and fault state at Ω=0.2

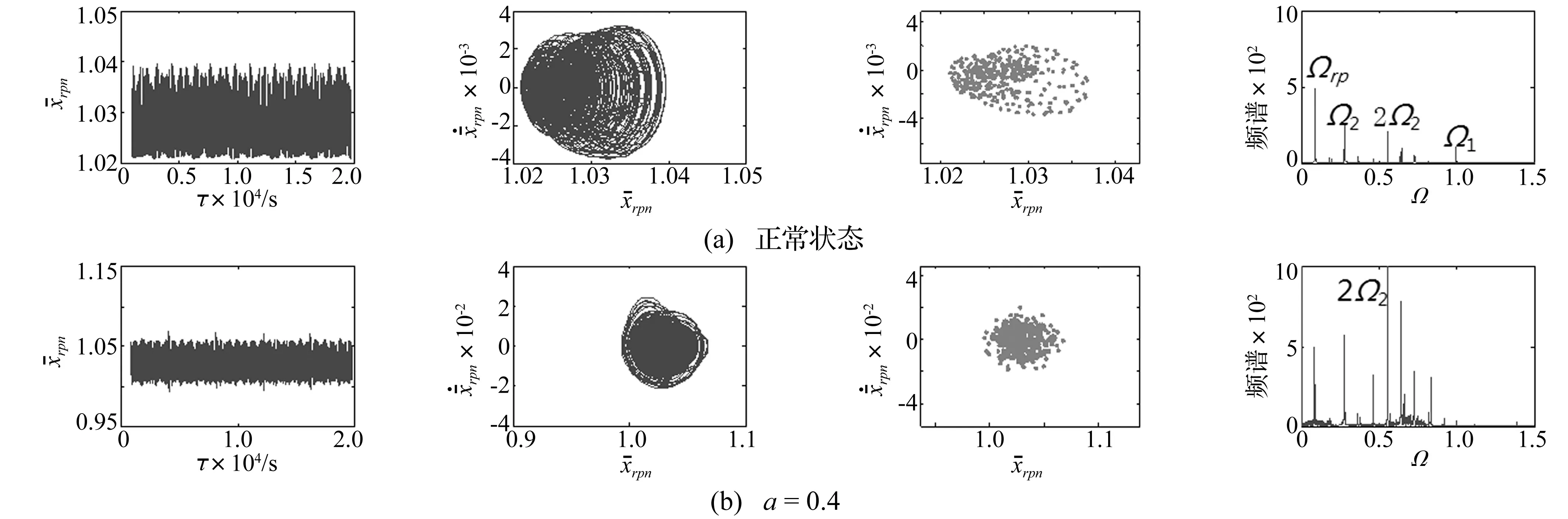
图6 Ω=1时正常及故障状态下行星轮振动响应变化Fig.6 The vibration response of planetary gear with normal and fault stateat Ω=1

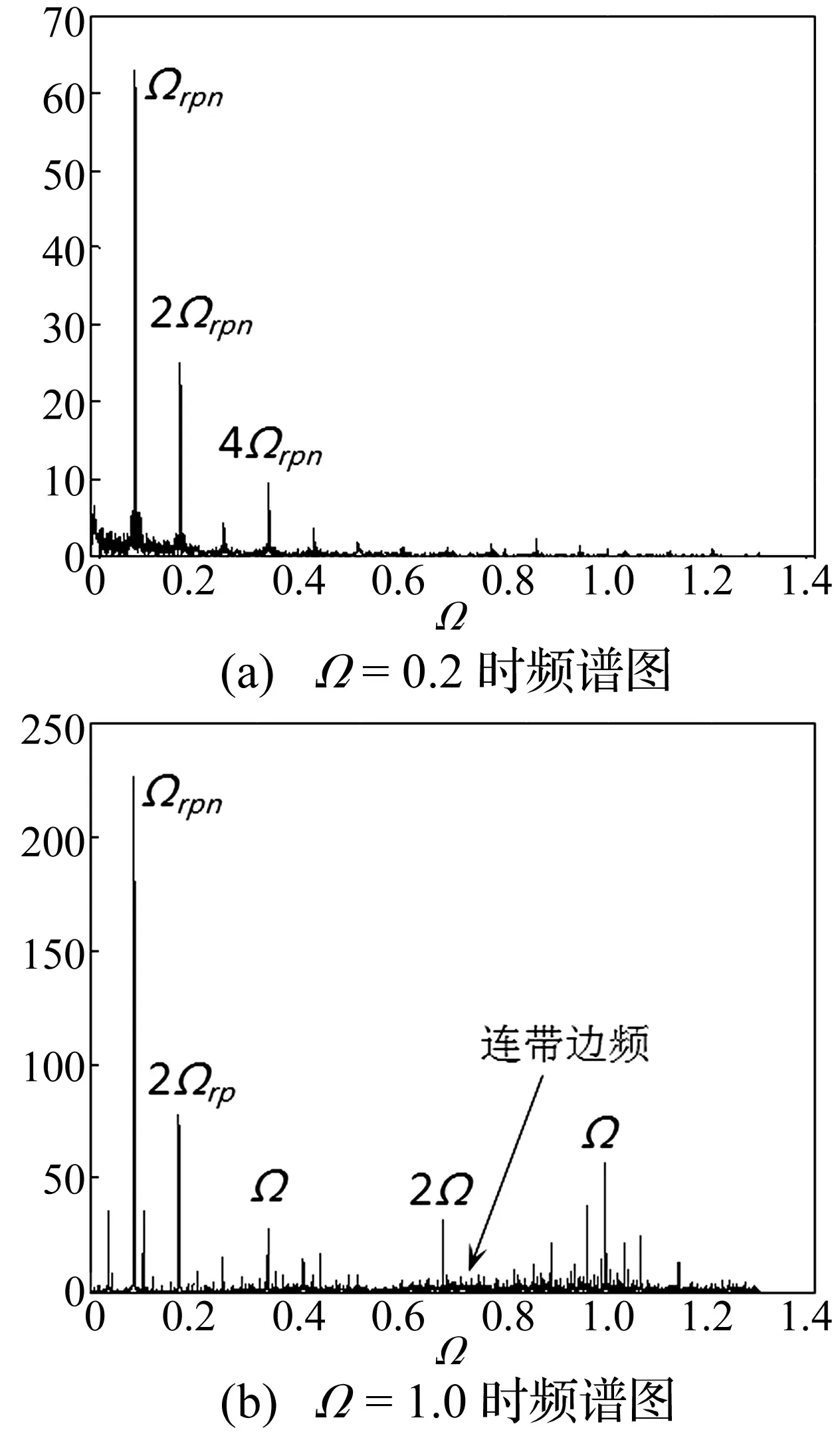
图7 故障状态下行星齿轮频谱Fig.7 Planetary gear spectrum with fault

由图7可见，Ω=0.2时行星轮啮合点处仅含行星轮啮合频率及其倍频，且故障边频明显；Ω=1时在2级定轴齿轮2倍频处发现大量含行星轮故障频率的边频。分别对比图5(b)与图7(a)，图6(b)与图7(b)的频谱图可见，仿真结果与实验结果一致。在没有仿真结果指导的情况下，Ω=1时2级定轴齿轮啮合频率2倍频处的大量边频容易误判为定轴故障，依据仿真结果证实其为行星轮断齿故障连带边频。

4 结 论

本文利用动力学仿真方法对比研究了正常与行星轮断齿故障的分岔特性及频谱特征，总结行星轮断齿故障的微弱特征及其连带故障特征，得出以下结论：

(1) 行星轮断齿故障使系统发生脱齿-碰撞现象，其故障特征在Ω较小时表现明显。在Ω=1时由于振动更为复杂，故障特征减弱。

(2)Ω较小时行星轮啮合点处的故障特征表现为行星轮啮合频率周围出现故障边频，该特征在实验信号中较清晰，容易识别。

(3)Ω=1时行星轮啮合点处的故障特征表现为2级定轴啮合频率及其2倍频幅值增大，且周围出现大量故障边频。该边频在实验信号中容易误判为定轴齿轮故障，依据仿真结果证实其为行星轮断齿故障连带边频。

(4) 通过仿真方法得到行星轮断齿故障的微弱特征及连带故障特征。依据故障微弱特征识别出实验信号中啮合频率处的故障信号；依据连带故障特征识别出非啮合频率处无法确定的由行星轮断齿故障引起的连带故障信号。解决了行星轮故障信号微弱难以辨识的问题，诊断出行星轮断齿故障。

[1] 徐玉秀, 赵晓清, 杨文平, 等. 多参数与多测点信息融合的行星轮故障诊断[J]. 仪器仪表学报, 2014(8):1789-1795. XU Yuxiu, ZHAO Xiaoqing, YANG Wenping, et al. Fault classification with multi-point based on SVM[J]. Chinese Journal of Scientific Instrument, 2014(8):1789-1795.

[2] 梁晓玉, 徐玉秀, 邢刚, 等. 行星齿轮传动系统复杂微弱故障的非线性特性[J]. 机械科学与技术, 2013, 34(4): 538-543. LIANG Xiaoyu, XU Yuxiu, XING Gang, et al. Nonlinear characteristics of complex and weak faults of planetary gear transmission system[J]. Mechanical Science and Technology for Aerospace Engineering, 2013, 34(4): 538-543.

[3] MOHANTY A R, KAR C. Fault detection in a multistage gearbox by demodulation of motor current waveform[J]. IEEE Transactions on industrial electronics, 2006, 53(4): 1285-1297.

[4] FENG Zhipeng, MING J Z, QU Jian, et al. Joint amplitude and frequency demodulation analysis based on local mean decomposition for fault diagnosis of planetary gearboxes[J]. Mechanical Systems and Signal Processing, 2013, 40: 56-75.

[5] FENG Zhipeng, MING J Z. Fault diagnosis of planetary gearboxes via torsional vibration signal analysis[J]. Mechanical Systems and Signal Processing, 2013, 36: 401-421.

[6] 雷亚国, 汤伟, 孔德同, 等. 基于传动机理分析的行星齿轮箱振动信号仿真及其故障诊断[J]. 机械工程学报, 2014, 50(7): 61-68. LEI Yaguo, TANG Wei, KONG Detong, et al. Vibration signal simulation and fault diagnosis of planetary gearboxes based on transmission mechanism analysis [J]. Journal of mechanical engineering, 2014, 50(7): 61-68.

[7] 秦大同, 龙威, 杨军, 等. 变风速运行控制下风电传动系统的动态特性[J]. 机械工程学报, 2012, 48(7): 1-8.QIN Datong, LONG Wei, YANG Jun, et al. Dynamic characteristics of wind turbine transmission system under varying wind speed and operation control conditions[J]. Journal of mechanical engineering, 2012, 48(7): 1-8.

[8] 秦大同, 田苗苗, 杨军. 变风载下风电齿轮传动系统动力学特性研究[J]. 太阳能学报, 2012, 33(2): 190-196. QIN Datong, TIAN Miaomiao, YANG Jun. Study on dynamic characteristics of gear transmission system of wind generator under varying wind load[J]. Acta energiae solaris sinica,2012, 33(2): 190-196.

[9] 秦大同, 邢子坤, 王建宏. 基于动力学和可靠性的风力发电齿轮传动系统参数优化设计[J]. 机械工程学报, 2008, 44(7): 24-31. QIN Datong, XING Zikun, WANG Jianhong. Optimization design of system parameters of the gear transmission of wind turbine based on dynamics and reliability[J]. Journal of mechanical engineering, 2008, 44(7): 24-31.

[10] 申永军, 杨绍普. 齿轮系统的非线性动力学与故障诊断[M]. 北京: 科学出版社, 2014.

[11] 张锁怀, 沈允文, 董海军, 等. 齿轮拍击系统的动力响应[J]. 振动工程学报, 2003, 16(1): 62-66. ZHANG Suohuai, SHEN Yunwen, DONG Haijun, et al. Dynamic response of a gear rattling system[J]. Journal of Vibration Engineering, 2003, 16(1): 62-66.

Chipping fault feature analysis for planetary gear in a gearbox transmission system

WANG Xin1,2, XU Yuxiu1,2, WU Baolin1

(1. School of Mechanical Engineering, Tianjin Polytechnic University, Tianjin 300387, China;2. Key Laboratory of Advanced Mechatronics Equipment Technology, Tianjin 300387, China)

In order to identify chipping fault characteristics and related fault characteristics of planetary gear in a wind turbine’s transmission system, dimensionless dynamic equations of the wind turbine gear transmission system containing a two-stage fixed-axis gear and a one-stage planetary gear were established. The fault characteristics of the system under the normal condition and those under planetary gear chipping fault condition with the variation of the excitation frequency were studied and compared. It was shown that the phenomenon of off tooth-collision, the fault characteristics and the related fault characteristics caused by the chipping fault of planetary gear are found; according to the simulation results the related fault signals caused by the planetary gear chipping fault are identified, they cannot be determined in past test signals, thus the planetary gear chipping faults with weak fault features are diagnosed.

planetary gear transmission; nonlinear dynamic systems; bifurcation; chipping fault; related failure characteristic

国家重大科技成果转化项目(2060403)； 天津市自然科学基金项目(10JCZDJC23400;13JCQNJC07000)

2015-08-17 修改稿收到日期：2015-10-23

王鑫 女，博士生，1985年5月生

武宝林 男，教授，博士生导师，1962年10月生

TH132.41

A

10.13465/j.cnki.jvs.2016.21.013