Cartesian积的局部边-路替换图的 L(2,1)-标号

2016-12-15吕大梅

浙江大学学报（理学版） 2016年6期

关键词：标号路标跨度

杜娟，吕大梅, 张科

(南通大学理学院，江苏南通 226007)

Cartesian积的局部边-路替换图的 L(2,1)-标号

杜娟，吕大梅, 张科

(南通大学理学院，江苏南通 226007)

设d为正整数，图G的一个L(d,1)-标号就是从非负整数集到V(G)的一个函数，且使得2个相邻顶点的标号相差至少是d，2个距离为2的顶点的标号相差至少为1. 图G的L(d,1)-标号的跨度就是所有L(d,1)-标号的最大值和最小值之差. 图G的L(d,1)-标号数是G的所有L(d,1)-标号下跨度的最小值. 在已有研究图G的边-路替换图的L(d,1)-标号基础上，研究了Cartesian积的局部边-路替换图的L(2,1)-标号.

频道分配；L(d,1)-标号；Cartesian积；局部边-路替换图

在频道分配问题上，需要将各个频率分配到各电台，如果2个距离很近的电台用接近的频率发送信息就会相互影响. 为了避免此类情况发生，其频率分配必须有足够大的距离. 而且，如果2个距离相近但不是很近的电台，分配的频率也必须不同. 此问题就是图G的距离2标号问题.

设d为正整数，图G的一个L(d,1)-标号就是从非负整数集到V(G)的一个函数，且使得2个相邻顶点的标号相差至少是d，2个相距为2的顶点的标号相差至少是1. 图G的L(d,1)-标号的跨度就是所有L(d,1)-标号的最大值和最小值之差. 图G的L(d,1)-标号数是G的所有L(d,1)-标号下跨度的最小值，用λd(G)表示.

1992年，文献 [1]提出L(2,1)-标号的概念，并猜想：当Δ≥2时，对任何图G，有λ(G)≤Δ2，其中Δ是图G的最大度. 此概念已被广泛研究，并延伸出许多具有挑战性的问题[2-12]. 在文献[13-14]的基础上，笔者研究了图G的边-路替换图G(Pk)(即用路Pk代替图G中的每条边所得的图)的L(d,1)-标号.

下文将研究k和l中一个等于2、另一个大于2的条件下Cartesian积的局部边-路替换图的L(2,1)-标号. 首先给出几个相关定义.

图G=(V，E)和H=(W，F)的Cartesian积G□H定义如下：

V(G□H)=V×W且E(G□H)={{(u,x),(v,y)}:u=v且(x,y)∈F，或者，x=y且(u,v)∈

E}=E1∪E2，其中，E1={{(u,x),(v,y)}:u=v且(x,y)∈F}，E2={{(u,x),(v,y)}:x=y且(u,v)∈E}.

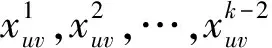
假设G和H是2个连通图，分别有m和n个顶点.方便起见，将图G□H的顶点看作在二维欧氏空间中的点. G□H中的每一个点都用坐标(a,b)来表示，其中a,b均为非负整数，且0≤a≤m-1,0≤b≤n-1. 对v=(a,b)∈V(G□H)， v是G□H第a行第b列的顶点，也是(G□H)(Pk,Pl)第a行第b列的节点.

由于(G□H)(P2,Pl)同构于(H□G)(Pl,P2)，故接下来研究在k≥3且l=2的条件下局部边-路替换图(G□H)(Pk,Pl)的L(2,1)-标号. 首先给出2个引理.

引理1[1]设G是最大度为Δ≥2的图，则λ(G)≥Δ+1.

引理2[1]设G是最大度为Δ≥2的图，若G包含3个度为Δ的顶点,且其中一个顶点与另外2个相邻，则λ(G)≥Δ+2.

由引理1, 下界是显而易见的：

λ((G□H)(Pk,P2))≥Δ+1.

对特殊的Δ1=1且Δ2=1，有

G□H≅P2□P2，且(P2□P2)(Pk,P2)≅C2k.

因此，

λ((P2□P2)(Pk,P2))=4.

下面研究Δ1,Δ2中至少1个大于等于2的情形.方便起见，设λ1=λ(G(Pk))，λ2=λ(H).

1 Δ1=1，Δ2≥2

定理1 设Δ2≥2且H不是顶点数小于5的路.

当k≥6，λ((P2□H)(Pk,P2))≤λ2+1；

当3≤k≤5，λ((P2□H)(Pk,P2))≤λ2+2.

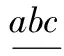
情形1 k≡0(mod 3)且k≠3. 当0≤x≤λ2-1时，如果x≠0,2,则替换路的标号为x(λ2+1)02402(λ2+1)x，否则为x(λ2+1)13513(λ2+1)x；当x=λ2时，用λ2+1替换节点(0, j)和(1, j)的标号λ2，并将替换路标为(λ2+1)(λ2-1)02402(λ2-1)(λ2+1)(λ2≥5)，(λ2+1)(λ2-1)04251(λ2-1)(λ2+1)(λ2=4).

情形2 k≡1(mod 3)且k≠4. 当0≤x≤λ2-1时，若x≠0,2,则把替换路标为x(λ2+1)240(λ2+1)x，否则标为0(λ2+1)142(λ2+1)0，2(λ2+1)130(λ2+1)2；当x=λ2时，用λ2+1替换节点(0, j)和(1, j)的标号λ2，并且把替换路标为(λ2+1)(λ2-1)130(λ2-1)(λ2+1)(λ2≥5)，(λ2+1)(λ2-1)140(λ2-1)(λ2+1)(λ2=4).

情形3 k≡2(mod 3)且k≠5. 当0≤x≤λ2-1时，如果x≠2,3,则把替换路标为x(λ2+1)2403(λ2+1)x，否则标为x((λ2+1))1420((λ2+1))x；当x=λ2时，用λ2+1替换节点(0, j)和(1, j)的标号λ2，并且把替换路标为(λ2+1)(λ2-1)0240(λ2-1)(λ2+1)(λ2≠5)，(λ2+1)(λ2-1)0250(λ2-1)(λ2+1)(λ2=5).

情形4 k=5.当0≤x≤λ2-2时，如果x≠0,则把替换路标为x(λ2+1)0λ2x，否则标为0(λ2+1)1λ20；当x=λ2时，用λ2+2替换节点(1,j)的标号λ2，并且把替换路标为(λ2+2)λ21(λ2-1)(λ2+2).当x=λ2-1时，替换路标为(λ2-1)(λ2+1)1(λ2+2)(λ2-1).

情形5 k=4.当x≠0，替换路标为x(λ2+2)0(x+1)，否则标为0p(λ2+2)1，其中p为节点0的邻点中未出现的标号.

情形6 k=3.若λ2为奇，替换路标为x(λ2+2)(λ2-x)；若λ2为偶，当x≠0时，替换路标为x(λ2+2)(λ2+1-x)，x=0时,标为0p(λ2+1)，其中p为节点0的邻点中未出现的标号，且当p=λ2时，改为0λ2(λ2+2).

综合以上情形，定理1得证.

2 Δ1≥2，Δ2≥2

定理2 设Δ1≥2，Δ2≥2.则当k≥8时，有λ((G□H)(Pk,P2))≤λ2+Δ1.

证明首先给出(G□H)(Pk,P2)第0行跨度为λ2的L(2,1)-标号. 当ki≥8，i=1,2,…,s时，置(G□H)(Pk,P2)的其余行标号与(G□H)(Pk,P2)的第0行相同. 假设节点标号为x. 当0≤x≤λ2-2时，此节点在替换路上的邻点用[λ2,λ2+Δ1-1]里的标号来标示，当x=λ2-1时，则此节点在替换路上的邻点用[λ2+1,λ2+Δ1]里的标号来标示，当x=λ2时，则用λ1+Δ2替换该节点的标号λ2，且该节点在替换路上的邻点用[λ2-1,λ2+Δ1-2]里的标号来标示. 由于Δ2≥2，λ2≥3，λ2+Δ1≥5，进而每一列的替换路都可在[0,λ2+Δ1]中被标号，abc表示重复结构，其中，p,q∈[λ2,λ2+Δ1-1]，a,b∈[λ2+1,λ2+Δ1]，r,s∈[λ2-1,λ2+Δ1-2]，具体如下：

情形1 k≡0(mod 3)且k≠3,6.

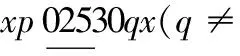
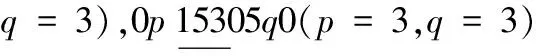
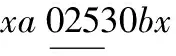
当x=λ2时，替换路标为

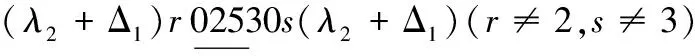
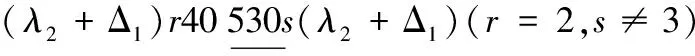
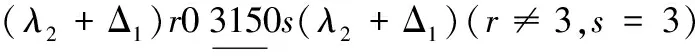
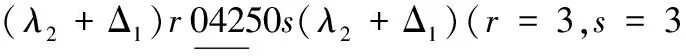
情形2 k≡1(mod 3)且k≠4,7.

当1≤x≤λ2-1时，替换路标为

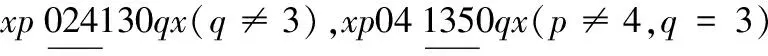
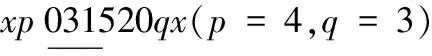
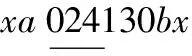
当x=λ2时，替换路标为

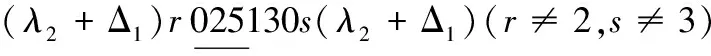
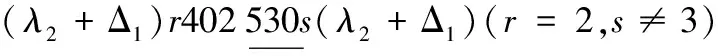
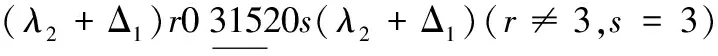
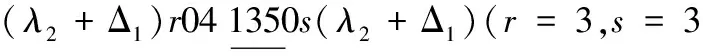
情形3 k≡2(mod 3)且k≠5.

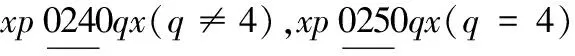
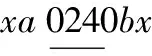
当x=λ2时，替换路标为

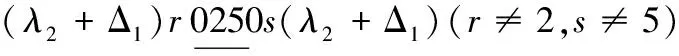
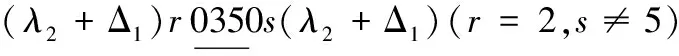
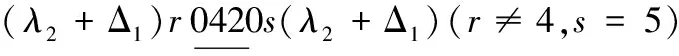
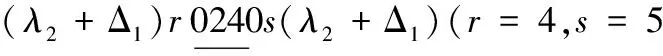
因此，当k≥8时，有

λ((G□H)(Pk,P2))≤λ2+Δ1.

类似可得如下结论.

定理3 假设Δ1≥2，Δ2≥2. 如果k≥6，那么λ((G□H)(P2,Pk))≤λ1+Δ2.

推论1 假设Δ1≥2，Δ2≥2. 如果k≥6，那么λ((G□H)(P2,Pk))≤min{λ1+Δ2,λ2+Δ1}.

3 Δ1≥2,Δ2=1

定理4 假设Δ1≥2,Δ2=1(即H为路P2). 则当k≥6时，有λ((G□P2)(Pk,P2))≤λ1+2.

证明给出(G□H)(Pk,P2)在0列的跨度为λ1的L(2,1)-标号f. 另一列标号为f+2. 如果在第0列的节点与对应第1列节点的邻点标号相同，将此第1列节点的邻点标号改为0；如果在第1列的节点与对应第0列节点的邻点标号相同，将此第0列节点的邻点标号改为 λ1+2. 则得到了(G□H)(Pk,P2)(k≥6)跨度为λ1+2的L(2,1)-标号，因此，λ((G□P2)(Pk,P2))≤λ1+2.

[1] GRIGGS J R, YEH R K. Labeling graphs with a condition at distance two[J]. Discrete Mathematics,1992(5):586-595.

[2] WHITTLESEY M A, GEORGES J P,MAURO D W. On theλ-number ofQnand related graphs[J]. Discrete Mathematics,1995(8):449-506.

[3] JHA P K, KLAZAR S, VESEL A. OptimalL(d,1)-labelings of certain directed products of cycles and Cartesian products of cycles[J]. Discrete Applied Mathematics,2005,152:257-265.

[4] JHA P K, NARAYANAN A, SOOD P, et al. OnL(2,1)-labeling of the Cartesian product of a cycle and a path[J]. Ars Combin,2000,55:81-89.

[5] JHA P K. OptimalL(2,1)-labelings of strong Cartesian products of cycles [J].Theory and Appl,2001,48:498-500.

[6] JHA P K, KLAZAR S,VESEl A.L(2,1)-labeling of direct products of pathes and cycles[J]. Discrete Applied Mathematics,2005,145:317-325.

[7] KUO D, YAN J H. OnL(2,1)-labeling of Cartesian products of pathes and cycles[J].Discrete Math,2004,238:137-144.

[8] JHA P K. OptimalL(2,1)-labeling of Cartesian products of cycles, with an application to independent domination, IEEE Trans Circ Syst-I:Fund[J]. Theory and Appl,2000,147:1531-1534.

[9] GEORGES J P, MAURO D W, STEIN M I. Labeling products of complete graphs with a conditionat distance two[J]. SIAM J Discrete Math,2000,14:28-35.

[10] ERWIN D J, GEORGES J P, MAURO D W. On labeling the vertices of products of complete graphs with distance constraints[J].Naval Research Logistics,2005,52(2):138-141.

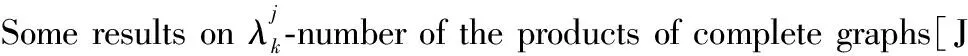
[12] SCHWARZ C, TROXELL D.L(2,1)-labeling of Cartesian products of two cycles[J].Discrete Appl Math,2006,154：1522-1540.

[13] LYU D M.L(2,1)-labelings of the edge-path-replacement of a graph[J]. J Comb Optim,2013,26(4):385-392.

[14] LYU D M, LIN N F.L(d,1)-labelings of the edge-path-replacement of a graph[J]. J Comb Optim,2013,26:819-831.

DU Juan, LYU Damei, ZHANG Ke

(SchoolofScience,NantongUniversity,Nantong226007,JiangsuProvince,China)

L(2,1)-labelings of the local-edge-path-replacements of Cartesian products. Journal of Zhejiang University(Science Edition), 2016,43(6):679-681

For a positive integerd, anL(d,1)-labeling of a graphGis an assignment of nonnegative integers to the vertices ofV(G) such that the difference between labels of adjacent vertices is at leastd, and the difference between labels of vertices whose distance are two aparts is at least 1. The span of anL(d,1)-labeling of a graphGis the difference between the maximum and minimum integers of all labels. TheL(d,1)-labeling-number ofGis the minimum span over allL(d,1)-labelings ofG. Based on the work ofL(d,1)-labels of the edge-path-replacement of a graphG, we study theL(2,1)-labeling of the local-edge-path-replacements of the Cartesian products.

channel assignment;L(d,1)-labeling; Cartesian product; local edge-path-replacement