一类超椭圆曲线上的有理点
2016-12-15杨仕椿汤建钢
杨仕椿, 汤建钢
(1. 阿坝师范学院 数学与财经系, 四川 汶川 623000; 2. 伊犁师范学院 数学与统计学院, 新疆 伊宁 835000)
一类超椭圆曲线上的有理点
杨仕椿1,2, 汤建钢2*
(1. 阿坝师范学院 数学与财经系, 四川 汶川 623000; 2. 伊犁师范学院 数学与统计学院, 新疆 伊宁 835000)
设p为素数,r≥0是整数.利用广义Fermat方程的深刻结论证明了:若3≤q<100,q≠31,则当p≥5时,超椭圆曲线yp=x(x+qr)上仅有平凡的有理点y=0;当q=5,11,23,29,41,47,59,83时,给出了该超椭圆曲线所有的有理点(x,y).特别地,当q=3且r=1时,证明了超椭圆曲线yp=x(x+3)仅在p=2时有非平凡的有理点(x,y),并给出了此时所有的非平凡有理点.
有理点;超椭圆曲线;广义Fermat方程
0 引 言
设x≥1,l≥2,k≥2,0≤d1<… yk=(x+d1)…(x+dl) (1) 有理点的研究引人注目[1-7].1975年,ERDÖS等[2]首先证明了超椭圆曲线(1)在dl=l时没有整点.随后,SANDER[3],LAKHAL等[4],SARADHA等[5-6]以及BENNETT[7]均对超椭圆曲线(1)进行了深入细致的探讨和研究,获得了一系列结果. 当l较小时,曲线(1)上的有理点研究似乎会变得困难一些.SANDER[3]、LAKHAL等[4]分别研究了当l≤5时方程(1)的情形.2004年,BENNETT[7]获得了当l=3,4,5时方程(1)的大量整数解.最近,利用Fermat方程以及广义Fermat方程[8-9]等相关方程的深刻结论,沈忠燕等[10-11]求出了曲线yk=x(x+2),yk=x(x+2)(x+3),yk=x(x+1)(x+3),以及曲线yk=x(x+2m)上所有的有理点,任霄等[12]求出了曲线yk=x(x+1)(x+3)(x+4)上当k≥3,k≠4时的所有有理点. 本文将运用沈忠燕等[10-11]的思路,利用广义Fermat方程的相关结论,考虑超椭圆曲线 yp=x(x+qr) (2) 上的有理点,其中p,q均为素数,r为非负整数.对满足3≤q<100的素数,以及q∈{5,11,23,29,41,47,59,83}和q=3且r=1的情形分别进行研究,获得了一些相应的结论. 引理1 令L和p均为素数,r为整数且3≤L<100,p≥5,0 xp+Lryp=zp (3) 除L=31外无非零整数解(x,y,z). 证明 见文献[13]中的定理15.5.3. 引理2 若p均为素数,且p≥11,0 xp+31ryp=zp (4) 无非零整数解(x,y,z). 证明 见文献[9]定理1. 引理3 若p均为素数,且p≡2,5(mod 9),则方程 x3+y3+cz3=0 (5) 在c=1,3,p,p2时(除c=2时的非零整数解(x,y,z)=(1,1,-1)外),无非零整数解(x,y,z). 证明 见文献[14]定理6.4.17. 定理1 设q为素数,且3≤q<100,q≠31,则当p≥5时,超椭圆曲线(2)上仅有平凡有理点y=0.若q=31,p≥11,则超椭圆曲线(2)上仅有平凡有理点y=0. cpb2=dpa(a+qrb). (6) 由于gcd(a,b)=gcd(c,d)=1,则gcd(b,a+qrb)=gcd(cp,dp)=1,因此,b2|dp且dp|b2,则b2=dp,于是方程(6)可化简为 cp=a(a+qrb), b2=dp. (7) 令gcd(a,a+qrb)=gcd(a,qr)=qδ,显然0≤δ≤r.由方程(7)可得,当p≥3时,存在互素的整数x1,z1以及整数y1,k,使得 (8) 且 其中,当δ=0时,k=0,当δ>0时,k≥0. 若δ=0,令r=pl+s,0≤s (9) 由引理1,可得当p≥5时,除q=31外,方程(9)无非零整数解(x2,y2,z2).若q=31,p≥11,由引理2,可得此时方程(9)也无非零整数解.因此,x1=y1=0,即a=c=0,代入式(2),可得y=0. 若0<δ≤r,且pk-δ>0,令r=pl+s,0≤s (10) 定理1得证. 定理2 设q∈{5,11,23,29,41,47,59,83},则超椭圆曲线(2)在p≥3时仅有平凡有理点y=0,在p=2时曲线(2)的所有有理点(x,y)满足 其中c1,c2为整数,且c1≠±c2. 证明 由定理1可知,如果q∈{5,11,23,29,41,47,59,83},则超椭圆曲线(2)在p≥5时仅有平凡有理点y=0. 当p=3时,令r=3l+s,0≤s<3,l,s为整数,由方程(8),可得 (11) 其中0≤δ≤r,且当δ=0时,k=0,当δ>0时,k≥0.若δ=0,由于q≡2,5(mod 9),则由引理3,可得该方程没有非零整数解(x,y,z).若0<δ≤r,则采用与定理1类似的讨论方法,通过比较方程两边q的指数,利用引理3,同理可得方程(11)无非零整数解. 定理2得证. 采用与定理1、2类似的证明方法,利用引理1以及引理3中c=3的结论,同理可得: 问题1 设p为素数,则超椭圆曲线yp=x(x+9)仅在p=2,3时有非平凡的有理点(x,y)? 问题2 设素数p≥3,则超椭圆曲线yp=x(x+14)仅在p=5时有非平凡的有理点(x,y)=(2,2)? 问题3 设p为素数,a为任意整数,则超椭圆曲线yp=x(x+a)上有哪些非平凡的有理点(x,y)? 以上问题有待进一步探索! 作者衷心感谢审稿专家的宝贵建议! [1] GUY R K. Unsolved Problem in Number Theory[M]. 3rd ed. New York:Springer-Verlag,2004:4. [2] ERDÖS P, SELFRIDGE J L. The product of consecutive integers is never a power[J]. Illinois J Math,1975,19:292-301. [3] SANDER J W. Rational points on a class of superelliptic curves[J]. J London Math Soc,1999,59:422-434. [4] LAKHAL M, SANDER J M. Rational points on the superelliptic Erdos-Selfridge curve of fifth degree[J]. Mathematika: A Journal of Pure & Applied Mathematics, 2003,50(1/2):113-124. [5] SARADHA N, SHOREY T N. Almost perfect powers in arithmetic progression[J]. Acta Arith,2001,99:363-388. [6] SARADHA N, SHOREY T N. Almost squares and factorisations in consecutive integers[J]. Compositio Math,2003,138:113-124. [7] BENNETT M A. Products of consecutive integers[J]. Bull London Math Soc,2004,36:683-694. [8] DARON H, MCREL L. Winding quotients and some variants of Fermat’s Last Theorem[J]. J Reine Angew Math,1997,490:81-100. [9] RIBET K A. On the equationap+2bp+cp=0[J]. Acta Arith,1997,79:7-16. [10] SHEN Z Y, CAI T X. Rational points on three superellipric curves[J]. Bull Aust Math Soc,2012,85:105-113. [11] 沈忠燕,蔡天新.超椭圆曲线yk=x(x+2m)上的有理点[J].中国科学:数学,2012,42(6):645-650. SHEN Zhongyan, CAI Tianxin. Rational points on a superelliptic curveyk=x(x+2m)[J]. Sci Sin Math, 2012,42(6):645-650. [12] 任霄,沈忠燕.超椭圆曲线yk=x(x+1)(x+3)(x+4)上的有理点[J].数学的实践与认识,2015,45(23):291-299. REN Xiao, SHEN Zhongyan. Rational points on a superelliptic curveyk=x(x+1)(x+3)(x+4)[J]. Mathematics in Practice and Theory, 2015,45(23):291-299. [13] COHER H. Analytic and Modern Tools[M]//Number Theory. New York: Springer,2007:511-514. [14] COHER H. Tools and Diophantine Equations[M]//Number Theory. New York: Springer, 2007:373-376. YANG Shichun1,2, TANG Jiangang2 (1.DepartmentofMathematicsandFinance,AbaTeachersUniversity,Wenchuan623000,SichuanProvince,China; 2.CollegeofMathematicsandStatistics,YiliNormalUniversity,Yinning835000,theXinjiangUygurAutonomousRegion,China) Rational points on a class of super elliptic curve. Journal of Zhejiang University(Science Edition), 2016,43(6):676-678 Letpbe a prime, andr≥0 be a integer. Using the deeply result of generalized Fermat equation, we prove that if 3≤q<100 andq≠31, then the superelliptic curveyp=x(x+qr) has only ordinary rational pointy=0 whenp≥5. Ifq=5,11,23,29,41,47,59,83, we give all of the rational points (x,y) in the superelliptic curve. Furthermore, ifq=3 andr=1, the superelliptic curveyp=x(x+3) has a non-trivial rational point (x,y) only whenp=2. rational point; super elliptic curve; generalized Fermat equation 2015-09-03. 新疆维吾尔自治区普通高等学校重点学科经费资助项目(2012ZDXK21);四川省高等教育人才培养质量教学改革项目(14-156-711);四川省教育厅自然科学研究项目(15ZA0337, 15ZB0348, 15ZB0350). 杨仕椿(1969-),ORCID:http://orcid.org/0000-0001-5692-7479,男,教授,主要从事数论、组合与编码研究. *通信作者,ORCID:http://orcid:org/0000-0001-7662-0394,E-mail:tjg@ylsy.edu.cn. 10.3785/j.issn.1008-9497.2016.06.009 O 156.1 A 1008-9497(2016)06-676-031 引 理
2 主要结论及证明
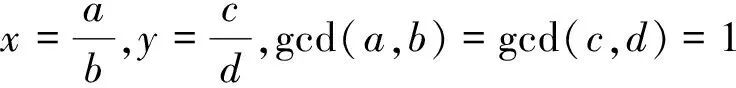





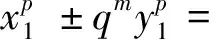


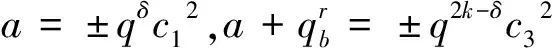

3 问 题

