增强工艺偏差容忍度的带隙基准电压源设计

2016-12-15罗小华卢宇峰李益航

浙江大学学报（理学版） 2016年6期

关键词：失配基准器件

俞淼, 罗小华, 卢宇峰, 李益航

(浙江大学超大规模集成电路研究所，浙江杭州 310027)

表1 不同工艺参数下的基准电压输出情况

表2 电流正态分布

增强工艺偏差容忍度的带隙基准电压源设计

俞淼, 罗小华*, 卢宇峰, 李益航

(浙江大学超大规模集成电路研究所，浙江杭州 310027)

随着CMOS工艺特征尺寸的减小，带隙基准电压源在制造过程中因器件失配和工艺波动易导致实际输出电压和目标值发生偏离，降低芯片成品率.为此提出将Pelgrom失配模型引入电路设计中，分别从器件参数、电路结构、版图布局三方面对亚微米级的电路进行工艺偏差优化.基于华润上华(CSMC)0.5 μm工艺以及Hspice软件仿真，显示基准源输出电压为1.232 54 V，偏差小于5 mV.流片测试结果表明,应用此设计的三通道LED驱动控制芯片成品率达到96.8%，输出电流达到(18±0.5)mA的芯片占99.6%以上.

工艺偏差；失配；带隙基准电压；阈值偏差；失调；成品率

带隙基准电压源具有高精度、低温漂、高电源抑制比等优点[1]，广泛应用于各种电路.随着CMOS工艺特征尺寸的进一步减小，工艺偏差对基准源电路性能和芯片成品率的影响越来越显著[2-3].主要表现为失配问题，即制造过程中由物理工艺上的偏离或随机波动导致设计上相同的2个或多个电阻或MOS管在参数或性能上有所差异[4].

针对失配问题，传统的解决方法主要有：①流片后根据基准电压的实测结果调整电阻值，使其输出电压满足要求，但会大大增加重复制版成本.②通过蒙特卡罗仿真预测并根据预测结果修改参数.蒙特卡罗分析是一种基于随机数预测结果的数学统计方法，即给定电路元器件参数容差的统计分布规律，具体流程为用伪随机数求得器件参数的随机抽样序列，分别对这些随机抽样序列进行直流、交流小信号和瞬态分析，根据多次分析的结果估算电路性能.但蒙特卡罗模型分析过程复杂且耗时长[5]，普适性不佳.本文提出在器件参数选取、电路结构设计和版图布局时引入失配模型，通过分析失配原因，优化参数，从而减轻失配造成的影响.

1 失配模型

目前用于计算失配的模型主要有2类：①适用于亚微米级的平方律模型[6]；②适用于深亚微米级、纳米级的BSIM3、BSIM4等模型.本文采用的工艺为亚微米级，因此以平方律模型为理论基础.器件失配的平方律模型来源于漏电流的数学方程，由偏差传递方程(POV)表征失配统计的方差σ2.设y是关于随机变量x的函数，y=f(x)，则y的绝对偏离误差Δy和方差σ2(y)可用式(1)表示：

(1)

模拟电路中，MOSFET通常在饱和状态下工作，结合式(1)和饱和电流公式，漏电流的偏差可表示为

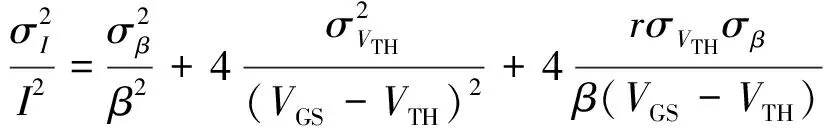
(2)

其中，r表示σVTH和σβ之间的相关系数.但理论和实验数据表明相关系数r值很小，可以忽略[6]，因此式(2)的末项可以舍去.漏电流的偏差可表示为

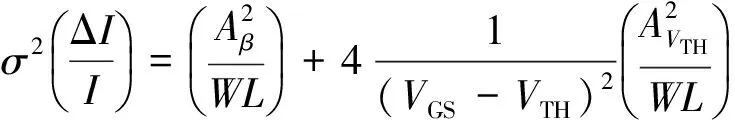
(3)

其中，Aβ和AVTH分别描述电流增益常数和阈值电压的偏差，其值由制造工艺决定.

在此基础上，PELGROM[7]指出，MOSFET的漏电流失配不仅与W、L相关，还与晶体管的间距、方向有关：

(4)

其中，W、L分别为MOSFET的沟道宽度和长度，DX是器件之间的距离，AP表示器件物理参数(如氧化层厚度、掺杂浓度、注入深度等)的随机误差，对器件的电学特性(如电流增益常数β、阈值电压VTH等)产生影响.SP描述的是器件物理参数的梯度误差，可以通过版图的共质心技术消除.由式(4)可得VTH和β的偏差表达式：

(5)

从电路参数设计的角度出发，可以忽略器件之间距离DX的影响.PAPATHANASIOU[8]在Pelgrom的基础上提出了更简化的失配模型：

(6)

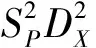
2 基于工艺偏差的核心电路设计

基于标准CMOS工艺，WIDLAR[9]于1971年提出了一种带隙参考电压源技术,得到不依赖于电源电压且不受温度影响的直流电压源.但实际带隙基准电压源会受温度和工艺偏差的影响，文献[10-12]分别提出了温度补偿方法.本文通过器件参数选取和电路结构设计来抑制工艺偏差.

2.1 基于失配的器件设计

模拟电路中，器件失配主要表现为由工艺偏差导致设计上相同的2个或多个电阻或MOS管在参数或性能上有所差异，从而影响最终的输出结果.根据式(4)，通过合理设置器件的W、L值可有效减小器件失配的局部偏差.针对MOSFET、电阻和三极管的失配问题，从电路参数选取上进行优化.

2.1.1 MOS管失配

2.1.2 电阻失配

根据式(4)，电阻的偏差可以表示为

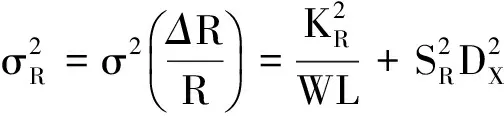
(7)

其中，KR是物理参数的随机偏差，由制造工艺决定；SR是物理参数的梯度误差，由布局布线时距离不等引起.

针对器件失配的局部偏差，可以忽略器件间距离DX的影响，因此电阻的偏差主要由W、L决定，面积大的匹配性能优于面积小的.根据精度要求，令偏差σR≤0.5%，由式(7)可得WL的最小值.结合电路设计上对阻值的约束条件，计算而得的电阻长度和宽度在满足电路设计的要求下有效抑制了失配.

2.1.3 三极管失配

带隙基准电压源电路中的三极管用标准CMOS工艺实现，如图1所示.其中N阱中的P+区作为发射区，N阱本身作为基区，P型衬底作为集电区，且集电极必须接地.相比于双极型工艺，这种垂直结构的PNP管的β值更小.

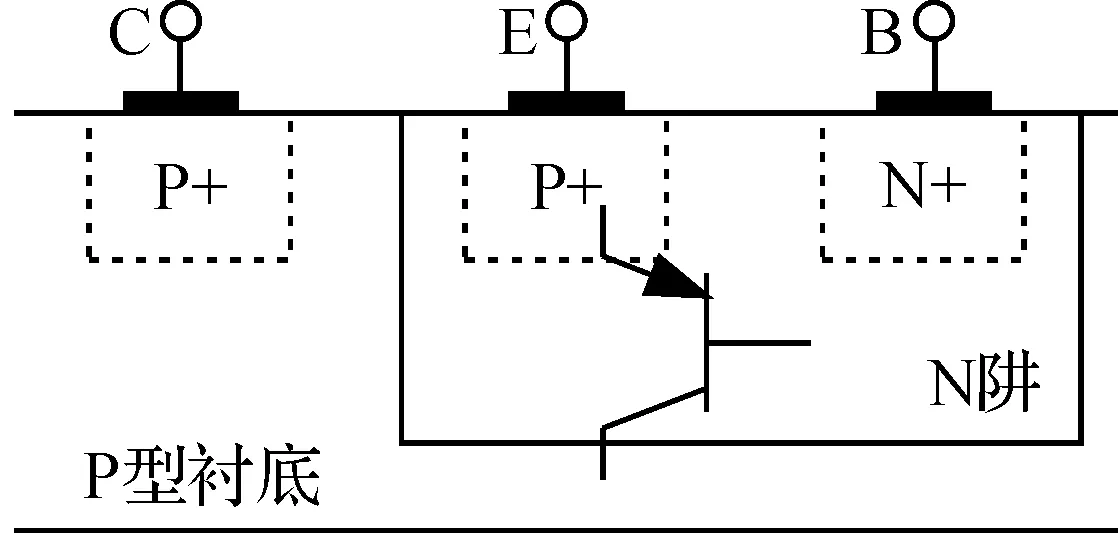
图1 CMOS工艺中三极管的实现Fig.1 Transistor in CMOS technology

在带隙基准电压源设计中，失配问题对ΔVBE的影响更为显著.在同一工艺下，设2个三极管的β和发射极电流IE都相等，发射极的面积之比为N，根据埃伯斯-莫尔方程，ΔVBE的表达式如式(8)所示：

(8)

其中，IE为发射极电流，rb为基区等效电阻，VT为热电压，是温度的电压当量，因此ΔVBE的偏差主要由电流增益常数β和基区等效电阻rb引起.根据式(5)，β的偏差可通过增大晶体管面积来抑制，但版图中晶体管模块所占比例较大，增大面积会显著增加制造成本.

2.2 基于工艺偏差的电路结构改进

通过合理选取参数可有效减少器件失配，但在实际电路中，小的器件偏差仍可能被放大输出，从而影响最终性能.本文从运算放大器偏差、运放失调影响和电流源偏差三方面来分析工艺偏差对带隙基准电压源的影响，并提出了参数改进方法.

2.2.1 运算放大器偏差分析

运放的失调分为系统失调和随机失调，系统失调主要由电路结构决定，而随机失调主要由差分输入管的失配引起.下文将分析图2所示电路结构的运放随机失调.

图2 运放电路图Fig.2 Schematic of OP-AMP

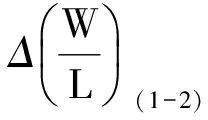
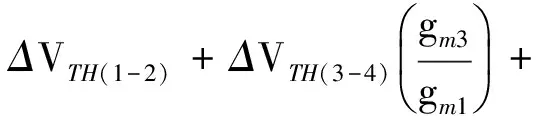
(9)其中,gm3、gm1分别为M3、M1的跨导，VOV(1-2)为M1、M2的过驱动电压差.结合阈值电压失配式(6)和失调电压式(9)，得到减小运放失调的方法:

①增大管子面积，减小由于阈值电压失配引起的失调；

③减小M1、M2的过驱动电压差.

2.2.2 运放失调对带隙基准电压的影响

带隙基准电压源的设计原理是利用三极管VBE的负温度系数特性和2个三极管之间ΔVBE的正温度系数相互抵消，使基准源输出电压的温度系数为0.运放失调电压的引入，使基准源的输出不再是单纯的VBE和ΔVBE的线性叠加.如图3所示，Vos表示运放的失调电压.

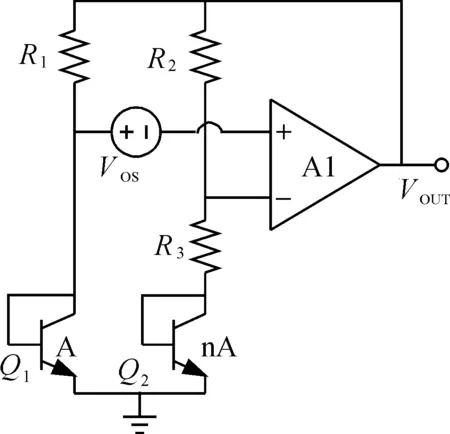
图3 含失调电压的带隙基准电压源电路Fig.3 Bandgap with offset voltage

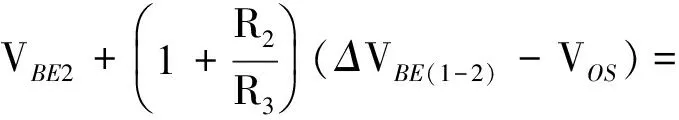
(10)

在匹配性设计的基础上，增大ΔVBE(1-2)可进一步减小运放失调电压带来的影响.结合式(10)和图3，增大ΔVBE(1-2)有2种方法：①设置R2=mR1，使Q1和Q2的集电极电流之比为m，则ΔVBE(1-2)=VTln(mn)，但电阻的失配远大于MOS管的失配[14]，不能满足有效减小偏差的设计目标.②每个分支都采用2个pn结串联，使ΔVBE(1-2)增加了一倍.但在标准CMOS工艺下(见图1)，PNP双极晶体管的串联形式很难实现，因此采用射极跟随形式.如图4所示，为了保障偏置电流具有相同的温度特性，用PMOS电流源(M1、M2、M3、M4)代替电阻.但双极晶体管射极跟随方式会增大基准源的输出电压，不符合输出电压在1.25 V左右的设计目标,因此通过引入M5支路进行电流复制，使输出满足要求.带隙基准电压源的输出电压为

(11)

图4 含电流源偏置的带隙基准电压源电路Fig.4 Bandgap with current source bias

2.2.3 电流源偏差影响

PMOS电流源的引入可确保晶体管的偏置电流具有相同的温度特性，但电流源的失配同时会引入偏差，从而影响带隙基准电压源的性能.其中PMOS电流源的失配主要由设计指标相同的M1、M2管之间以及M3、M4管之间的阈值电压的偏差引起.设M1和M2有阈值偏差ΔVTH(1-2)，M3和M4有阈值偏差ΔVTH(3-4)，则由电流源M1、M2的阈值电压偏差引起的ΔVBE为

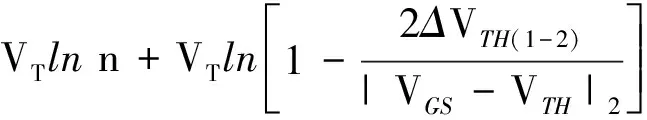
(12)

其中，ID1、ID2是M1、M2提供的偏置电流，|VGS-VTH|2是M2的过驱动电压.阈值电压偏差较小，根据ln(1+α)≈α(α→0)和式(12)，由M1和M2的阈值偏差引起的基准源输出电压偏差可近似为

(13)

同理可得由M3和M4的阈值偏差引起的基准源输出电压偏差为

(14)

同一工艺下，ΔVTH1=ΔVTH2=ΔVTH[15]，且M2、M4的过驱动电压相等.由式(13)、(14)得电流源阈值偏差引起的基准源输出电压偏差为

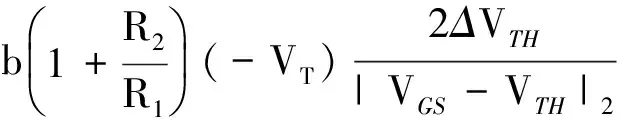
(15)

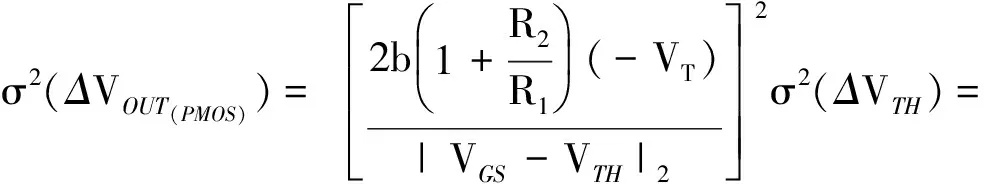
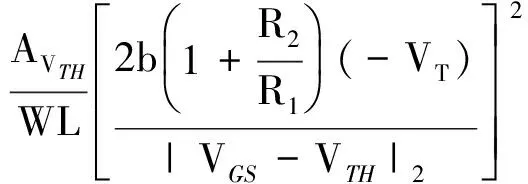
(16)

3 版图优化

3.1 MOS管的版图布局

由于在光刻及圆片制造过程中不同轴向将产生不同特性，因此需要着重考虑版图布局中相同设计参数的MOS管对称性问题.本文采用的晶体管宽度较大，若使用2个管子沿x轴并排放置，相邻2个管子之间会引起栅氧电容变化ΔCOX，则沿x轴上会有显著的梯度误差.而采用交叉耦合布局，可有效抑制线性梯度效应.如图5所示，将晶体管分成2个宽度为原来一半的晶体管，其中MOS管M1由相距最远的m1a、m1b并联而成，M2由相邻的m2a、m2b并联而成.M1流过的电流为m1a、m1b上的电流之和，M2流过的电流为m2a、m2b上的电流之和，则β1=μn(COX+COX+3ΔCOX)=β2，有效抑制了线性梯度效应.而添加虚拟晶体管可以保证m1a+m1b和m2a+m2b的周围环境一致，进一步减小偏差.

图5 MOS管版图Fig.5 Layout of MOSFET

3.2 电阻的版图布局

根据式(4)，电阻的整体偏差受梯度误差和电阻间距的影响.因此采用共质心交叉布局，即使用相同的单位电阻通过串联或并联的方式来保证取向相同.如图6所示，将R1和R2分成较短的电阻单位，平行放置呈相间排布，可有效提高R1和R2间的匹配性.

图6 电阻版图Fig.6 Layout of resistance

3.3 三极管的版图布局

三极管在版图设计上采用共质心对称布局，来减小梯度误差.如图7所示，Q1置于布局中心，Q2以8个等面积的晶体管呈环绕式相连，这种对称性设计有利于晶体管周围的环境保持一致，从而减小失配偏差.式(8)中提到的基区等效电阻主要由连线电阻和接触孔电阻组成，可采用多打接触孔和宽金属连线等方法抑制偏差.

图7 三极管版图Fig.7 Layout of transistor

4 实验结果与分析

基于工艺偏差设计的带隙基准电压源模块已应用于三通道LED驱动控制芯片中，并完成CSMC 0.5 μm工艺下的流片.如图8所示，芯片总面积为595×743 μm2，带隙基准电压模块面积为179×316 μm2，占12.8%.通过不同工艺角(corner)下Hspice对输出电压的直流仿真和芯片输出电流的实测结果来验证此设计，可有效抑制工艺偏差造成的影响，保证芯片的成品率.

图8 LED驱动芯片版图Fig.8 Layout of LED driver chip

4.1 Hspice仿真结果

基于MOS管和电阻的工艺偏差，对带隙基准电压源输出电压进行CSMC 0.5 μm工艺下的Hspice仿真.表1为供电电压5 V、温度25 ℃时在不同工艺角下的直流仿真.典型情况下基准电压值为1.232 54 V，不同corner下的偏差范围为±4.9 mV.图9所示为-20～140 ℃时不同corner情况下的直流仿真结果.电阻偏差相同时，同一温度下，3种情况MOS管的偏差基本在±1 mV以内，符合0.1%的指标要求.MOS管偏差相同时，同一温度下，3种情况电阻偏差较大，基本在±5 mV以内，这符合电阻失配较严重的理论分析和0.5%的指标要求.

表1 不同工艺参数下的基准电压输出情况

Table 1 Output voltage in different corners

图9 -20～140 ℃时不同corner情况下的直流仿真Fig.9 DC response in different corners(T is from-20 to 140 ℃)

4.2 流片测试结果

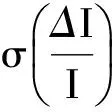
图10 RGB三通道电流分布Fig.10 Currents of RGB channels

表2 电流正态分布

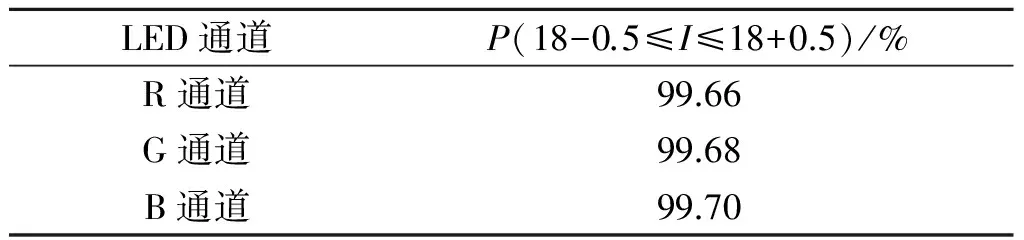
Table 2 Normal distribution of currents

5 结论

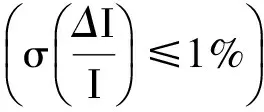
[1]IVANOVV,BREDERLOWR,GERBERJ.Anultralowpowerbandgapoperationalatsupplyfrom0.75V[J]. Solid-State Circuits, 2012,47(7):1515-1523.

[2] BANERJEE A, CHATTERJEE A. Signature driven hierarchical post-manufacture tuning of RF systems for performance and power[J]. IEEE Transactions on Very Large Scale Integration Systems, 2015,23(2):342-355.

[3] RADFAR M, SINGH J. A yield improvement technique in severe process, voltage, and temperature variations and extreme voltage scaling[J]. Microelectronics Reliability, 2014, 54(12):2813-2823.

[4] 刘博,张雷鸣,王金婵.基于D/A转换器的工艺波动表征方法的研究[J].微电子学与计算机,2015，3(3):117-121. LIU Bo, ZHANG Leiming, WANG Jinchan. Research on characterization methodology for process variation with D/A converters[J]. Microelectronics & Computer,2015,3(3):117-121.

[5] 吕伟锋,孙玲玲.一个简单的65 nm MOSFET失配模型[J].计算机辅助设计与图形学学报,2011,23(7):1280-1284. LYU Weifeng, SUN Lingling. A simplified 65 nm MOSFET mismatch model[J]. Journal of Computer-Aided Design & Computer Graphics, 2011,23(7):1280-1284.

[6] LAKSHMIKUMAR K R, HADAWAY R A, COPELAND M A. Characterization and modeling of mismatch in MOS transistors for precision analog design[J]. IEEE Journal of Solid-State Circuits, 1986,21(6):1057-1066.

[7] PELGROM M. Matching properties of MOS transistors[J]. IEEE Journal of Solid-State Circuits,1989,305(3):1433-1439.

[8] PAPATHANASIOU K. A designer’s approach to device mismatch: Theory, modeling, simulation techniques, scripting, applications and examples[J]. Analog Integrated Circuits & Signal Processing, 2006,48(2):95-106.

[9] WIDLAR R J. New developments in IC voltage regulators[J]. IEEE Journal of Solid-state Circuits,1971,6(1):2-7.

[10] 代国定,徐洋,李卫敏，等.高性能分段温度曲率补偿基准电压源设计[J].浙江大学学报：工学版,2010(11):2142-2147. DAI Guoding, XU Yang, LI Weimin， et al. Design of high performance bandgap reference based on piecewise temperature curvature compensated technology[J]. Journal of Zhejiang University: Engineering Science,2010(11):2142-2147.

[11] 汤华莲,庄奕琪,张丽，等.一种可校准的低温漂基准电流源[J].西安电子科技大学学报：自然科学版,2013,40(4):130-136. TANG Hualian, ZHUANG Yiqi, ZHANG Li, et al. Design of a trimmed current reference with a low temperature drift[J]. Journal of Xidian University: Natural Sciences,2013,40(4):130-136.

[12] 张献中,张涛.一种三阶曲率补偿带隙基准电压源的设计[J].武汉科技大学学报,2015(1):67-71. ZHANG Xianzhong, ZHANG Tao. A bandgap voltage reference with third-order curvature compensation[J]. Journal of Wuhan University of Science and Technology,2015(1):67-71.

[13] KINGET P R. Device mismatch and tradeoffs in the design of analog circuits[J]. IEEE Journal of Solid-State Circuits, 2005,40(6):1212-1224.

[14] GUPTA V, RINCN-MORA G. Predicting and designing for the impact of process variations and mismatch on the trim range and yield of bandgap references[C]//Quality of Electronic Design, ISQED 2005. Sixth International Symposium on IEEE. San Jose :IEEE,2005:503-508.

[15] LYU Weifeng, SUN Lingling. Modeling of current mismatch induced by random dopant fluctuation in nano-MOSFETs[J]. Chinese Journal of Semiconductors,2011(8):46-50.

YU Miao, LUO Xiaohua, LU Yufeng, LI Yihang

(InstituteofVLSIDesign,ZhejiangUniversity,Hangzhou310027,China)

Bandgap voltage reference design with enhanced tolerance of process variations. Journal of Zhejiang University(Science Edition), 2016,43(6):689-695

As the feature size of CMOS technology is scaled down, devices mismatch and process tolerance will lead to deviation in bandgap reference voltage, which significantly impacts manufacturing cost by decreasing yield. Based on the Pelgrom’s mismatch model, this paper proposes a design methodology from three aspects: parameters, schematic and layout. Hspice simulation result shows that the output of the bandgap reference circuit is (1.232 54±0.005)V in CSMC 0.5 μm technology. Applying this design in 3 channels LED driver chips, the test results indicate that the yield reaches 96.8%, while the chips that meet the output current requirements of (18±0.5) mA account for above 99.6%.

process variations; mismatch; bandgap voltage reference; threshold deviations; offset; yield