非光滑多目标分式规划的对偶条件

2016-12-15李向有

浙江大学学报（理学版） 2016年6期

关键词：对偶分式广义

李向有

(延安大学数学与计算机学院, 陕西延安 716000)

非光滑多目标分式规划的对偶条件

李向有

(延安大学数学与计算机学院, 陕西延安 716000)

最优性问题在研究博弈理论、目标规划、最低风险问题等方面有重要应用，利用非光滑分析，定义了一类新的广义不变凸函数，研究了涉及此类函数的多目标半无限分式规划问题, 得到了参数对偶问题的弱对偶和严格逆对偶条件，在新的凸性下得到了一些重要结论.

广义不变凸函数；多目标；对偶；分式规划

推广凸函数是最优化理论一个重要的研究方向， ANTCZAK[1]在B凸函数和(p,r)凸函数的基础上定义了可微B-(p,r)凸函数，并用其研究单目标规划问题，文献[2-7]在B-(p,r)凸函数的基础上推广了不变凸函数，用于研究不同类型的规划问题，并得到了大量有益的结果. 虽然利用B-(p,r)凸函数研究规划的文献不少，但大多是利用可微B-(p,r)凸函数讨论单目标规划问题和多目标可微规划问题，涉及多目标非光滑规划问题的研究很少. 利用非光滑分析研究多目标规划问题已成为近年来研究的热点，文献[8-10]利用不同的凸函数研究了非光滑多目标规划问题，得到了许多重要结果.

本文在上述研究的基础上，定义了一类B-(p,r,a)不变凸函数、B-(p,r,a)不变拟凸函数、B-(p,r,a)不变伪凸函数，研究多目标半无限分式规划的对偶问题，在新的凸性下，得到了一些重要结果.

1 基本定义

若对任意x∈Rn，存在一个正数k和x的邻域N(x)，对任意y,z∈N(x)，使得

‖f(y)-f(z)‖≤k‖y-z‖，

则称实值函数f:Rn→R是局部Lipschitz的[11].

若函数f为局部Lipschitz的，那么函数f:X→R在点x处沿方向d的Clarke广义方向导数和Clarke广义梯度分别定义为[11]：

∂f(x)={ξ∈Rn:f0(x;d)≥ξTd,∀d∈Rn}.

注对于任意x,y∈Rn,下面变量间的序关系始终成立：

已有文献在利用B-(p,r)凸函数讨论规划问题时，只讨论B-(p,r)凸函数中的1种，其他3种情况类似可证. 本文也照此思路，只给出在p,r≠0时B-(p,r,a)不变凸函数的定义.

定义1 设非空开集X⊂Rn,f:X→R是X上的局部Lipschitz函数，p,r是任意非零实数，u∈X,若∀x∈X，存在向量函数η:X×X→Rn，函数b:X×X→R+(R+是非负实数)，a:X×X→R，使得对∀ξ∈∂f(u)有

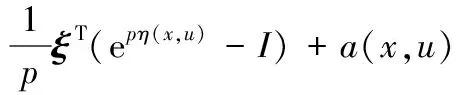
则称f在u点为关于函数η的B-(p,r,a)不变凸函数.

定义2 设非空开集X⊂Rn,f:X→R是X上的局部Lipschitz函数，p,r是任意非零实数, u∈X, 若∀x∈X，存在向量函数η:X×X→Rn，函数b:X×X→R+(R+是非负实数)，a:X×X→R，对∀ξ∈∂f(u)有

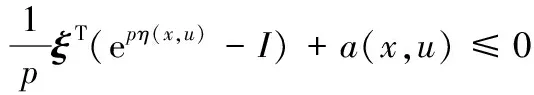
则称f在u点为关于函数η的B-(p,r,a)不变拟凸函数.

定义3 设非空开集X⊂Rn,f:X→R是X上的局部Lipschitz函数，p,r是任意非零实数，u∈X,若∀x∈X，存在向量函数η:X×X→Rn，函数b:X×X→R+(R+是非负实数)，a:X×X→R，使得对∀ξ∈∂f(u)有

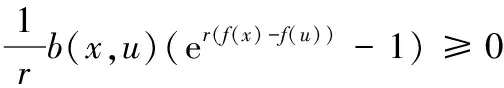
则称f在u点为关于函数η的B-(p,r,a)不变伪凸函数.其中，I=(1,1,…,1)∈Rn，e(a1,a2,…,an)=(ea1,ea2,…,ean)∈Rn.

2 对偶性条件

考虑下列多目标半无限分式规划问题：

s.t h(x,u)0,

x∈X0⊆Rn, u∈Y⊂Rn,

其中，fi:Rn→R,gi:Rn→R(i=1,2,…,m),h(x,u):Rn×Rn→R均为局部Lipschitz的实值函数，并假设fi(x)≥0,gi(x)>0,i=1,2,…,m,Y为无限可数参数集.记Δ={jh(x,uj)0,uj∈Y⊂Rn},是可数指标集，假定下面出现的关于h(x,u)的广义级数都是绝对收敛的.

(FP)的对偶规划定义为

(FD)Max v=(v1,v2,…,vm),

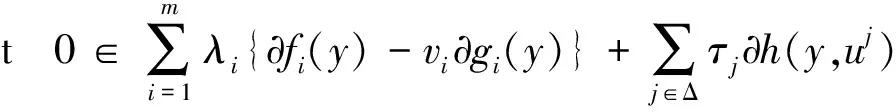
(1)

fi(y)-vigi(y)0, i=1,2,…,m,

(2)

τjh(y,uj)0, j∈Δ,

(3)

(4)

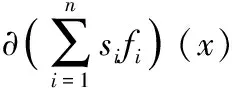
定理2(弱对偶) 令

(1)x,(y,λ,τ,v)分别是(FP)和(FD)的可行解;

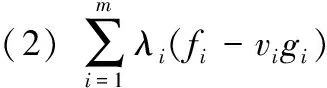
(3) a(x,y)+c(x,y)≥0.

fi(x)-vigi(x)≤0, i=1,2,…,m,

且至少存在某个k,fk(x)-vkgk(x)<0.

结合式(2)，可以得到

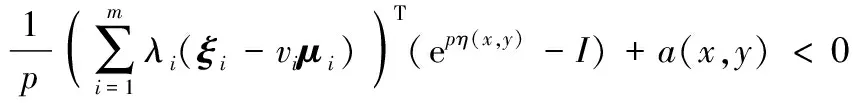
(5)

由式(1)可知，∃ξi∈∂fi(y),μi∈∂gi(y),δj∈∂h(y,uj),有

(6)

由式(5),(6)和a(x,y)+c(x,y)≥0，可得

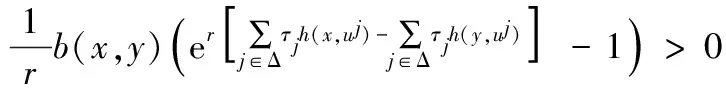
即

(7)

又x,(y,λ,τ,v)分别是(FP)和(FD)的可行解，故τjh(x,uj)0,τjh(y,uj)0，这与式(7)矛盾，故假设不成立.

证明类似于文献[12]定理2的证明.

定理4(严格逆对偶) 令

(1)x0,(y,λ,τ,v)分别是(FP)和(FD)的可行解;

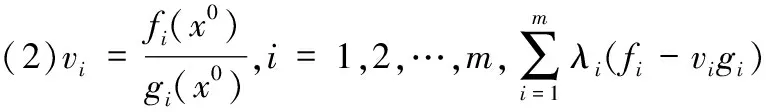
(3)a(x0,y)+c(x0,y)>0.

则x0=y,即y也是(FP)的有效解.

证明由推论1可知，x0,(y,λ,τ,v)分别是(FP)和(FD)的有效解.假设x0≠y，因为x0,(y,λ,τ,v)分别是(FP)和(FD)的可行解,所以 τjh(x0,uj)0τjh(y,uj)，即有

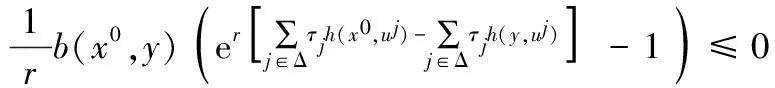
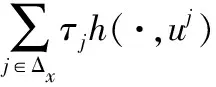
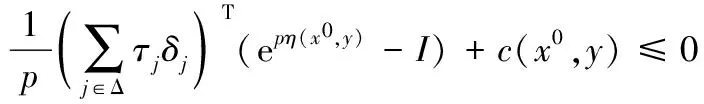
(8)

由式(1)可知，∃ξi∈∂fi(y),μi∈∂gi(y),δj∈∂h(y,uj),有

(9)

由式(8),(9)和a(x0,y)+c(x0,y)>0，可得

即有

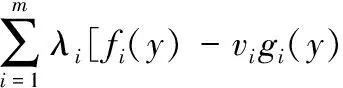
而这与式(2)矛盾，故x0=y,即y也是(FP)的有效解.

[1] ANTCZAK T. A class ofB-(p,r) invex functions andmathematical programming[J]. J Math Anal Appl，2003,286:187-206.

[2] ZHANG Y, ZHU B, XU Y T. A class of LipschitzB-(p,r)-invex functions and nonsmooth programming[J]. OR Transactions,2009,13(1):61-71.

[3] ANTCZAK T, SINGH V. GeneralizedB-(p,r)-invexity functions and nonlinear mathematical programming [J]. Numercial Functional Analysis and Optimization,2009,30:1-22.

[4] 万轩,彭再云.B-(p,r)-预不变凸规划的Mond-weil对偶问题研究[J].重庆师范大学学报,2011,28(1):1-7. WAN Xuan, PENG Zaiyun.The research of mond-weir duality for programming withB-(p,r)-preinvexity function [J]. Journal of Chongqing Normal University,2011,28(1):1-7.

[5] ANTCZAK T. Generalized fractional minimax programming withB-(p,r)-invexity[J]. Computer and Mathematics with Applications,2008,56:1505-1525.

[6] 李向有,张庆祥.广义I型函数的对偶性条件[J].贵州大学学报,2014,31(2):22-24. LI Xiangyou, ZHANG Qingxiang.Dual conditions of generalized I type functions[J]. Journal of Guizhou University,2014,31(2):22-24.

[7] ANTCZAK T, SINGH V. Optimality and duality for minimax fractional programming with support function underB-(p,r)-Type I assumptions[J]. Mathematical and Computer Modelling,2013,57(S5/6):1083-1100.

[8] JAYSWAL A, PRASAD A K, STANCU-MINASIAN I M. On nonsmooth multiobjective fractional programming problems involving (p,r)-ρ-(η,θ) invex functions[J]. Yugoslav Journal of Operations Research,2013,23:367-386.

[9] MISHRA S K, LAI K K, SINGH V. Optimality and duality for minimax fractional programming with support function under (c,α,ρ,d)-convexity[J]. Journal of Computional and Applied Mathematics,2015,274:1-10.

[10] GUPTA R, SRIVASTAVA M. Optimality and duality for nonsmooth multiobjective programming using G-type I functions[J].Applied Mathematics and Compution,2014,240(4):294-307.

[11] CLARKE F H. Optimization and Nonsmooth Analysis[M]. New York: Wiley-Interscience,1983.

[12] KUK H, LEE G M, TANINO T. Optimality and duality for nonsmooth multiobjective fractional programming with generalized invexity[J]. Journal of Mathematical Analysis and Applications,2001,262(1):365-375.

LI Xiangyou

(InstituteofMathematicsandComputerScienceofYan’anUniversity,Yan’an716000,ShaanxiProvince,China)

Duality conditions of nonsmooth multi-objective fractional programming. Journal of Zhejiang University(Science Edition), 2016,43(6):682-684

Optimization plays an important role in game theory, goal programming, minimum risk problems, etc. By nonsmooth analysis, a new class of invex functions are defined, and multi-objective semi-infinite fractional programming problems involving the new defined invex functions are investigated. Then, weak dual conditions and strictly converse dual conditions of parameter dual problems are obtained, and some important conclusions are also drawn under the new convexity.

generalized invex functions ; multiobjective ; duality ; fractional programming