基于Kalman滤波和奇偶矢量法的优化RAIM算法

宋　恺，范胜林，刘建业，王昕洋

（南京航空航天大学导航研究中心，南京211106）

基于Kalman滤波和奇偶矢量法的优化RAIM算法

宋恺，范胜林，刘建业，王昕洋

（南京航空航天大学导航研究中心，南京211106）

针对传统RAIM算法很难检测微小伪距偏差的问题，可以通过对多个历元的统计检验量进行归一化处理，增大统计检验量的非中心化参数，提高对微小故障的检测率。Kalman新息检测法可以对卫星的故障进行独立检测，具有运算量小、在少星情况时仍能进行故障检测和识别的优点，但是对微小伪距偏差不敏感。针对两种方法的优点提出了基于Kalman滤波和奇偶矢量法的综合RAIM算法。仿真结果表明，该方法不仅可以提高对微小伪距偏差的检测率，同时减少了对可见卫星数的要求，验证了该算法应用于接收机自主完好性检测的可行性和正确性。

RAIM；Kalman滤波；奇偶矢量法；微小伪距偏差

0 引言

完好性检测是指当导航系统发生任何故障或者导航定位超过允许限值时，导航系统应当具备及时发现故障并通知用户的能力［1］。接收机自主完好性检测（ReceiverAutonomousIntegrity Monitoring，RAIM）通过接收机的冗余观测量进行一致性检验来检测识别故障。RAIM具有不依赖外部设备、成本低、易于实现等优点，是一种广泛应用的完好性检测方法。

RAIM算法可分为两类，一类是基于Kalman滤波的算法，另一类是基于伪距残差的快照算法。Kalman滤波算法具有能够在少星情况下正常检测的优势，快照算法包括最小二乘法［2］与奇偶矢量法［3］，两者本质上相同。RAIM的故障检测率与故障卫星的伪距偏差以及可见卫星数有关，当伪距偏差达到门限时以及可见卫星数满足基本要求时才能有效检测。

针对Kalman新息检测法在微小伪距偏差下检测性能不强以及奇偶矢量法在可见卫星数较低时不能良好检测的问题，本文提出了一种将Kalman新息检测法与累积奇偶矢量法［4］结合的新算法。该方法针对伪距偏差和可见卫星数进行识别，尽可能得到最优的故障检测结果。经过仿真实验对不同情况下的故障检测率进行验证分析，证明了该方法的正确性和适用性。

1 Kalman新息检测法

RAIM的本质实际上是对随机变量的假设检验。传统快照算法是利用当前时刻的量测数据进行计算，对冗余变量有着严格的要求。当冗余变量个数较少时，不能有效检测和识别故障卫星，限制了完好性检测的性能。

实际测量中，时域量测数据表现出来的统计特征也能够反映随机变量的特性。如果有故障出现，就会影响数据的平稳性和遍历性，因此能够依据有无故障，时域信息所表现的不一致性进行故障检测［5］。同时运用时域的处理技术，能够最大限度地利用历史量测数据，从而增加当前历元冗余变量个数，就不需要像传统算法一样对可见卫星数有过高的要求。因此，将一致性假设检验与时域处理技术相结合来完成卫星故障检测是可行且必要的。

1.1 新息方差法原理分析

系统随机线性离散方程为［6］：

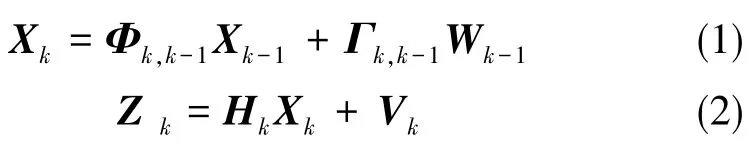
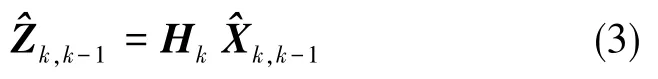
K时刻观测值Zk与预测值＾Zk，k-1的差值为Kalman新息向量，定义为：

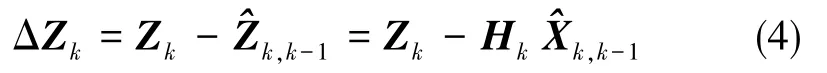
ΔZk为高斯白噪声误差列向量，令可以推出新息方差MK为：

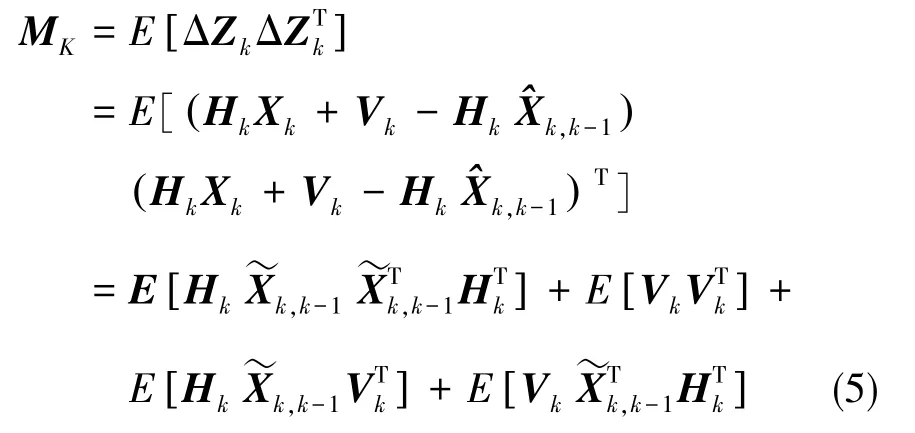
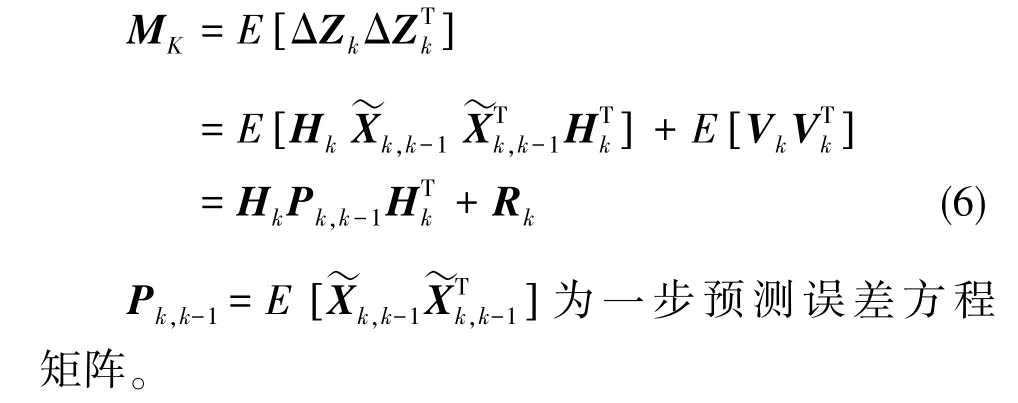
1.2 新息检测法门限的确定

由Kalman滤波理论可知，新息变量ΔZk服从零均值高斯分布，则其中为无故障新息方差。令则：

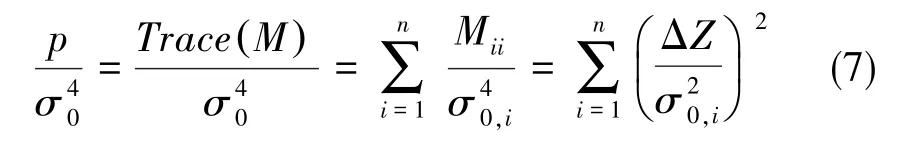
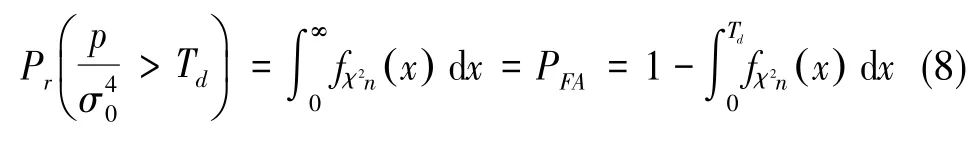
2 奇偶矢量法

2.1 传统奇偶矢量法

对GNSS伪距观测量进行线性化处理，模型可表示为［7］：

式中，X是4维用户状态向量，包括3个位置矢量和1个接收机时钟偏差；G是n×4维观测矩阵；ε为n×1维观测噪声矢量；Y是观测伪距与实测计算伪距差值构成的n×1维矢量。

假设系统没有伪距观测误差时，系统模型可表示为：

将观测矩阵G进行QR分解：

其中，Q为n×n的正交矩阵，R是n×4维的上三角矩阵，带入观测模型并两边左乘QT：

QT和R可以表示为：

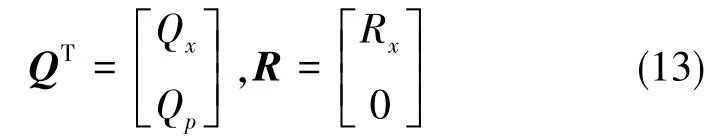
其中，Qx为QT前4行，Qp为QT的后n-4行，Rx为R的前4行，则式（13）可以表示为：

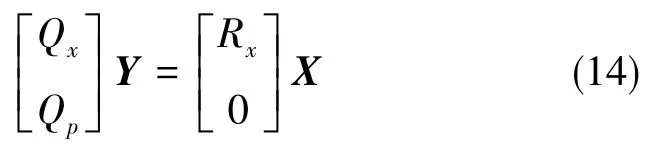
可以得到X的近似解：

同时有QpY=0，考虑伪距观测误差ε，有Y= GX+ε，则：

构造奇偶矢量法的故障检测统计量：

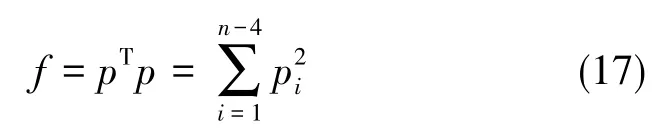
当系统无故障时，f服从自由度为n-4的中心X2分布；当系统存在故障时，f服从自由度为n-4的非中心X2分布。非中心化参数为：

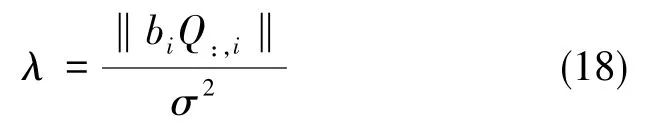
其中，bi为第i颗卫星出现的伪距偏差。可以看出在恒定虚警率下，奇偶矢量法的检测性能与非中心化参数λ有关［8］，并且在大故障情况下具有良好的检测性能。而对于微小偏差，由于非中心化参数较小，导致检测成功率降低，甚至无法检测，因此传统奇偶矢量法对微小伪距偏差的检测存在不足。

2.2 改进的奇偶矢量法

针对伪距偏差较小时的微小慢变故障，假设其在短时间内（小于2min）是不变的，构造新的奇偶矢量为连续N个历元奇偶矢量的累加：

pi为第i历元的奇偶矢量，N为累加历元的个数并假定这N个历元中可见卫星数不变。否则奇偶矢量矩阵Q也会变化，不符合奇偶矢量的累加条件。由此可以得到新的统计检测量：

将新的检测统计量与检测门限进行比较来判断出是否发生故障。

积累奇偶矢量的统计特性为：

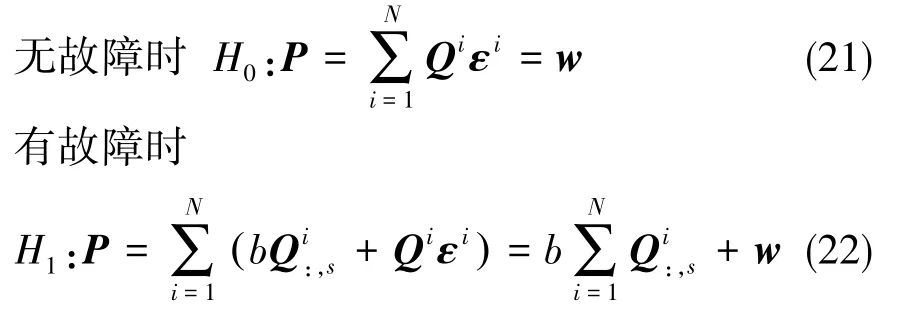
其中，Qi为第i个历元时的奇偶变换矩阵，εi为第i个历元时的量测噪声，P为n-4维矢量，w为P的量测噪声矢量。由于Qi的行向量单位正交，可知w的分量Qiεi=wi之间相互独立，且服从均值为零、方差为σ′2=Nσ2的高斯随机分布。

在前面的假设中，短时间内卫星的可见卫星数和几何构型不变，则奇偶变换矩阵Qi的变化很小，可以近似为列向量在这段时间内不变，有：

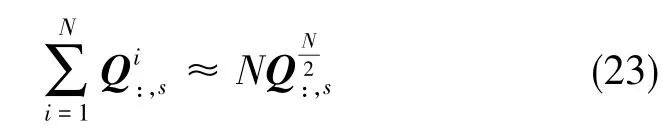
在存在故障情况下：

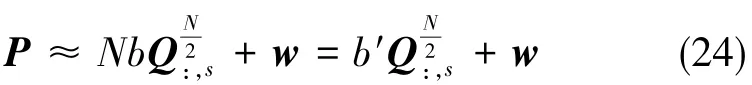
积累奇偶矢量P的等效故障偏差可以表示为：

由式（25）可以得出：

归一化后积累奇偶矢量统计检验量的统计特性为：

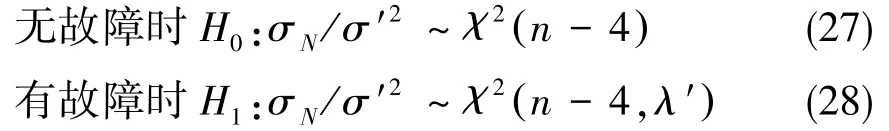
非中心化参数λ′：

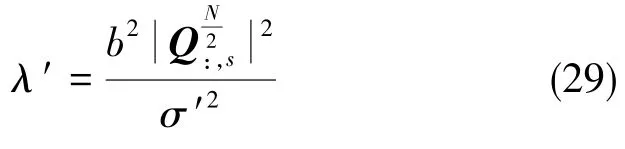
新旧非中心化参数比为：

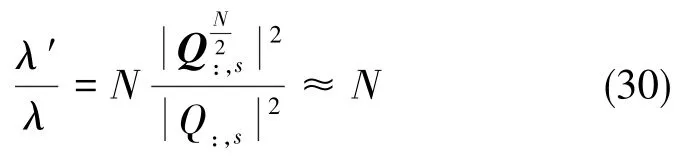
新方法的非中心化参数扩大了N倍，因此可以对微小故障问题进行检测，提高了故障检测性能。

3 基于Kalman滤波和奇偶矢量法的优化RAIM算法

Kalman新息检测法利用时域信息进行故障的检测与排除，相比传统RAIM算法，增加了当前时刻的冗余变量个数，所以在卫星个数较少时仍然能进行故障检测与识别。然而由于滤波器的记忆效应，新息检测法对缓慢变化的斜坡故障不敏感，检测能力将会大大下降。本文提出了一种将Kalman新息检测法与改进的奇偶矢量法结合的新算法，改进的奇偶矢量算法能够弥补Kalman滤波算法在微小慢变故障下的不足，并且具有大故障下检测的优点，Kalman新息检测法弥补了在少星情况下的缺陷。

首先对可见卫星进行识别，如果可见卫星数小于5颗，由于奇偶矢量法不可用，采用Kalman新息检测法进行检测。之后对故障是否为微小故障进行识别，定义伪距偏差b小于15m时为微小伪距偏差，此时采用累积奇偶矢量法；而发生大故障时，因为奇偶矢量法和新息检测法都能良好识别，考虑到算法的简化性，采用Kalman新息检测法。综合算法的流程图如图1所示。

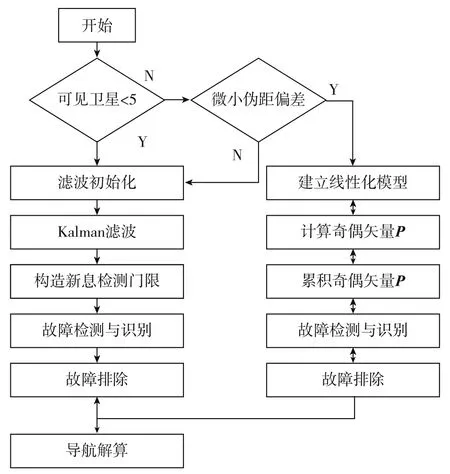
图1　综合RAIM算法流程图Fig.1 Flow chart of comprehensive RAIM

4 仿真实验

为了验证Kalman新息检测法和累积奇偶矢量法综合算法的优化性能，采用仿真手段进行分析与验证。实验采用STK仿真北斗卫星导航系统，共14颗卫星，包含5颗IGSO卫星，5颗GEO卫星以及4颗MEO卫星。仿真5min采样时间为1s的北斗卫星数据，共301个历元，卫星截止高度角为10°，误警率取1×10-6，漏检率取1×10-4。

取σ=0．2m为等效测距误差，在可见卫星1上加入0m～3m的微小慢变伪距偏差，取10历元奇偶矢量累加进行仿真，仿真结果如图2所示。

由图2可知，累积奇偶矢量法在伪距偏差为0．799m时，算法的故障检测率达到100％。此时传统奇偶矢量法的检测率只有6．76％。当伪距偏差达到2．48m时，故障检测率才达到100％。经过分析可得当系统发生微小伪距偏差时，累积奇偶矢量法检测性能要优于传统奇偶矢量法，在相同微小慢变伪距偏差下，累积奇偶矢量法的故障检测率要高于传统RAIM算法，验证了新算法的正确性和优越性。

在可见卫星1上加入0m～3m的伪距偏差，采用Kalman新息检测法和改进的综合算法进行仿真，仿真结果如图3所示。

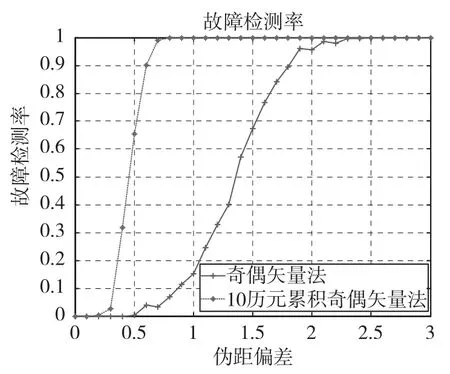
图2　积累奇偶矢量法故障检测率Fig.2 Fault detect rates with accumulated parity vector RAIM

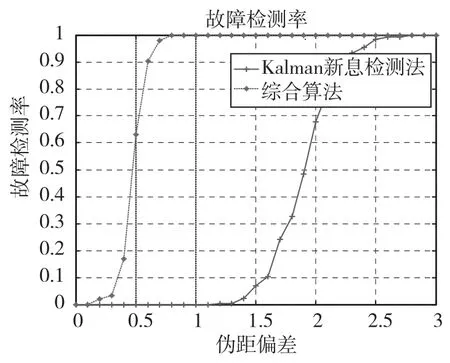
图3　微小伪距偏差下故障检测率Fig.3 Fault detect rates under weak pseudorange bias

由图3可以得出，在综合算法下，伪距偏差达到0．799m时故障检测率已经接近100％，此时Kalman新息检测法的检测率为0％，还无法有效检测出故障，直到伪距偏差达到2．773m时才达到100％。由此可以看出综合算法在微小伪距偏差下的故障识别率优于Kalman新息检测法，新算法极大地提高了微小伪距偏差下的故障检测率。

设定为4颗可见卫星，在卫星1上加入伪距偏差，其中取σ=6m为等效测距误差。此时奇偶矢量法将不可用，图4所示为综合算法的仿真结果，可以看出新算法依然能够正确的检验。在伪距偏差达到130m时，故障检测率达到100％，弥补了奇偶矢量法在少星情况下无法检测的缺陷。

经过上述分析和仿真实验可以得出，将Kalman新息检测法与改进的累积奇偶矢量法进行结合的综合算法具有良好的检测性能。在微小慢变故障下，能够有效地进行故障检测，克服了新息故障法对慢变斜坡故障不敏感的问题，当可见卫星数目较小时，克服了传统RAIM不能有效检测的缺陷。

图4　4颗可见卫星情况下故障识别率Fig.4 Fault detect rates with 4 satellites in view

5 结论

本文提出了一种将Kalman新息检测法与累积奇偶矢量法相结合的综合接收机自主完好性检测（RAIM）算法。本算法主要针对传统RAIM算法在微小伪距偏差情况下检测率低以及奇偶矢量法在少星情况下无法检测的问题，结合了Kalman新息检测法在少星情况下能够正常检测的优势和积累奇偶矢量法对于微小慢变故障的良好检测性能。

本文首先分析了Kalman新息检测法和奇偶矢量法以及累积奇偶矢量法的基本原理，然后提出了新的优化RAIM算法的原理与流程。采用北斗卫星导航系统进行仿真实验，分别仿真了在少星情况和微小微距偏差下系统的故障检测率。由上述分析结果，在发生微小微距偏差情况下，新算法的故障检测率要高于新息检测法与传统奇偶矢量法，故障检测率有较大提升，弥补了Kalman新息检测法对微小故障不敏感的特性。当可见卫星数较少时，奇偶矢量法不能有效检测，新算法依然能够有效检测，弥补了奇偶矢量法的不足，验证了新算法的适用性和理论的正确性。我国北斗二代卫星导航系统还在不断的发展建设中，自主完好性检测是卫星导航系统中必不可少的一部分，本算法对北斗接收机自主完好性检测具有一定意义。

［1］吴云．GNSS接收机自主完备性监测算法研究［D］．武汉大学，2009．WUYun．AlgorithmresearchonGNSSreceiver autonomousintegritymonitoring［D］．Wuhan University，2009．

［2］吴杰，彭敖，石江宏．基于部分可见星的接收机完好性监测方法［J］．导航定位学报，2016，4（1）：25⁃32．WU Jie，PENG Ao，SHI Jiang⁃hong．A receiver autono⁃mous integrity monitoring method based on positioning result of proportion of visible satellites［J］．Journal of Nav⁃igation and Positioning，2016，4（1）：25⁃32．

［3］Bhattacharyya S，Gebre⁃Egziabher D．Kalman filter⁃based RAIM for GNSS receivers［J］．IEEE Transactions on Aero⁃space＆Electronic Systems，2015，51（3）：2444⁃2459．

［4］Parkinson B W，Axelrad P．Autonomous GPS integrity monitoring using the pseudorange residual［J］．Navigation，1988，35（2）：255⁃274．

［5］Sturza M A．Navigation system integrity monitoring using redundant measurements［J］．Navigation，1988，35（4）：483⁃501．

［6］刘文祥，李峥嵘，王飞雪．一种可检测和改正微小慢变伪距偏差的新RAIM方法［J］．宇航学报，2010，31（4）：1024⁃1029．LIU Wen⁃xiang，LI Zheng⁃rong，WANG Fei⁃xue．A new RAIM method for detecting and correcting weak pseudor⁃ange bias under gradual change［J］．Journal of Astronau⁃ tics，2010，31（4）：1024⁃1029．

［7］娄上月．接收机自主完好性监测及系统仿真研究［D］．哈尔滨工程大学，2012．LOUShang⁃yue．Researchonreceiverautonomous integrity monitoring and the simulation system［D］．Harbin Engineering University，2012．

［8］付梦印，邓志红，张继伟．Kalman滤波理论及其在导航系统中的应用［M］．北京：科学出版社，2003．FU Meng⁃yin，DENG Zhi⁃hong，ZHANG Ji⁃wei．Kalman filtering theory and its application in navigation system［M］．Beijing：Science Press，2003．

［9］Kaplan E D，Hegarty C．Understanding GPS：principles and applications［M］．Artech House，2006．

［10］沙海，黄新明，刘文祥，等．基于非相干积累的微小伪距偏差RAIM方法研究［J］．宇航学报，2014，35（6）：708⁃712．SHA Hai，HUANG Xin⁃ming，LIU Wen⁃xiang，et al．Research on the RAIM method based on non⁃coherent ac⁃cumulation for tiny pseudo⁃range bias［J］．Journal of As⁃tronautics，2014，35（6）：708⁃712．

［11］邓志鑫，李隽，刘孟江．卫星导航RAIM多星故障检测与识别方法研究［J］．导航定位学报，2016，4（1）：75⁃79．DENG Zhi⁃xin，LI Jun，LIU Meng⁃jiang．Research on multi satellite failure detection and recognition method of satellite navigation RAIM［J］．Journal of Navigation and Positioning，2016，4（1）：75⁃79．

An OPtimized RAIM Algorithm Based on Kalman Filter and Parity Vector

SONG Kai，FAN Sheng⁃lin，LIU Jian⁃ye，WANG Xin⁃yang
（Navigation Research Center，Nanjing University of Aeronautics and Astronautics，Nanjing 211106）

As traditional RAIM algorithm is very difficult to detect small pseudorange deviation，an algorithm is pro⁃posed to increase the decentralization parameters and improved the monitoring rate of tiny fault by normalization processing of statistical tests with multiple epochs．The fault of each satellite can be detected by Kalman innovation covariance inde⁃pendently and it has the advantage of monitoring and identification when the visible satellites are less，but Kalman innova⁃tion algorithm is not sensitive to tiny pseudorange fault．A comprehensive RAIM algorithm is proposed biased on the advan⁃tages of Kalman innovation covariance and parity vector algorithm．The simulation results show that the new algorithm can not only improve the monitoring rate of small pseudorange deviation，but also reduce the requirements of visible satellites，the result verifies the algorithm is applied to the receiver autonomous integrity test feasibility and correctly．

RAIM；Kalman filter；parity vector；tiny pseudorange

P228．4

A

1674⁃5558（2016）05⁃01266

10．3969／j．issn．1674⁃5558．2016．06．017

2016⁃04⁃11

国家自然科学基金（编号：61533008，61374115）；中央高校基本科研业务费专项资金资助（编号：NZ2016104，NP2015406，NP20152212）。

宋恺，男，导航、制导与控制专业，硕士，研究方向为卫星导航定位、接收机自主完好性检测。