基于机器学习的动态基线及其在银行网络流量数据监测中的应用

左昌盛 宋 歌

(平安银行股份有限公司，广东 深圳 518034)



基于机器学习的动态基线及其在银行网络流量数据监测中的应用

左昌盛 宋 歌

(平安银行股份有限公司，广东 深圳 518034)

随着金融科技的快速发展，基于网络流量数据的性能管理、风险防范，尤其是异常流量检测逐渐引起人们的重视。然而，传统基于固定基线的流量检测方法不能适应逐渐增多的数据及日渐复杂的数据类型，导致其检测结果不准确而产生错误警报，同时也大大耗费人力物力。本文提出基于机器学习方法中主成分分析及最小二乘支持向量回归机的动态基线预测及检验方法，实现了动态基线的自主构造及对异常指标数据的自动检测。实际仿真结果表明，本文所提方法与基于加权方法的动态基线相比，能更好地实现异常检测与预警。

动态基线；流量检测；分级预警；机器学习

1.引言

近年来，随着银行业信息化建设的日趋完善，增强银行风险防范水平是银行业发展的必然要求。一方面，稳定高效的信息系统可以提高银行交易的便利性和管理的有效性；另一方面，随着物联网、大数据、云计算等新技术的发展和应用，无处不在的数据正以前所未所的方式改变着人们的工作和生活。因此，数据分析已成为信息管理的重要和有效途径。特别地，针对网络流量数据的监测，由于银行交易量大，涉及范围广，对由此产生的大量原始数据进行手工人为检测将消耗大量的人力物力，并且效率低，不全面。因此，设计基于数据挖掘技术的异常流量自动检测系统是必要的。

对此，本文设计基于主成分分析(PCA)[1]及最小二乘支持向量回归机(LS-SVR)[2]的动态基线预测模型。具体地，本文利用主成分分析方法对预处理过的原始数据构造综合指标以增加可解释性，并构造线性及非线性最小二乘支持向量回归机模型，实现动态基线值的预测。同时，设计基于阈值技术的动态预警机制，使得流量异常时能够实现实时预警。

2. 动态基线模型

本节将实现基于网络流量数据的多指标体系的动态基线预测及预警。假设一天截取数据节点数有m个，已监测l天。每个节点流量用n个特征指标描述。记xij=(xij1，…，xijn)∈Rn为第j天第i个节点流量，其中xijk是xij的第k个流量指标值，i=1，2，…，m，j=1，2，…，l，k=1，2，…，n。

2.1 综合指标构建

为考虑多个特征指标对基线值的综合作用，同时为区分每个特征的贡献率，本文利用由多个指标构成的综合指标做基线值预测。具体地，将采取主成分分析技术。

记

则主成分分析优化问题如下：

s.t.vTv=1,v∈Rn，

(1)

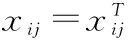
此时，矩阵X变换成一个列向量，综合指标也得以构造。值得注意的是，此时v*是二维向量，其分量分别为两个特征指标的在综合指标中的权重。

2. 2 动态基线回归

为实现基线值的预测，下面对综合指标构造回归模型。对固定的i，i=1，2，…，m，考虑数据集{(1,xi1),…，(l,xil)}。根据综合指标的特点，可选择线性或非线性LS-SVR。记A=(1,2,…，l)T，Yi=(xi1,xi2,…，xil)T，e=(1,1,…,1)T∈Rl。对线性回归，设所求解的回归方程为f(z)=wz+b，其中w,b∈R为欲求系数，z为变量。则该线性回归问题可由以下最小二乘支持向量回归机(LS-SVR)实现：

s.t.(Aw+eb)-Y=ζ,

(2)

其中C>0是一个调节参数。

由于模型(2)采用线性等式约束，且考虑平方损失函数，因此求解速度较快。事实上，优化问题(2)可通过其对偶问题求解，且本质上只相当于求解一个线性方程组。具体地，设α∈Rl为问题(2)的对偶变量，则求解a和b需求解以下线性方程组

(3)

由(2)求解得到a和b后，可得预测函数为

(4)

其中zi为A的第i行(第i个样本点)，z为未知预测的样本点。

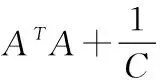
为预测新的一天，即第l+1天的动态基线值，将z=l+1代入到(4)中，得到的f(z)值记为yi，则yi即为由前l天历史数据得到的新的一天第i个节点处的基线值。具体实现中，可采用以下两种方法。

(一)全天节点同时预测：由l天全天数据预测l+1天的数据。这时，默认一天内各节点间没有直接关系，因此可以实现批量预测。

(二)单个节点逐个预测：前l天前n小时的数据预测第l+1天前n小时的数据。l=1时，对于确定的n，可以实现第2天前n个小时的预测。这时，对于第2天第n个小时后的第1个节点预测，可用第2天前n个小时的数据作为历史数据。由于一天之内各节点的数据值显然呈非线性，因此这时需采用非线性回归。此时，当时间节点跨越一天时，可不受不同天的限制，但n值需事先取定。相对于方法一，该方法计算量相对较大。

方法二与方法一相比其所应用技术相同，而处理的具体数据不同。因此，下面本文只考虑方法一。

2. 3 异常流量预警

pi=|xi,l+1-yi|.

理论上，pi的值越小，则实际数据xi,l+1与该节点基线值yi越接近。此时，可根据具体数据特点，确定阈值0≤δ1<δ2<δ3。当pi≤δ1时，断定流量正常；当δ1δ3时，为严重警告。

为了合理确定阈值警告界线，我们采取添加噪声法。具体地，其步骤如下：

(a) 在原始数据中添加强度为0的白噪声数据，并认为此时的p值的峰值为该模型这次添加白噪声之后的轻微警告界限。由于一次实验，存在极大的偶然性，因此将这一过程重复N次，最终取N次p值的峰值的均值(记为δ1)为该模型的轻微警告阈值。实际中，可以根据数据量的大小、数据处理速度的要求等确定N值。

(b) 添加强度为1的白噪声数据，重复过程(a)，可得该模型的中度警告界限(δ2)。

(c) 添加强度为2的白噪声数据，重复过程(a)，可得该模型的严重警告界限(δ3)。

(d) 通过上述三步，可以得到某一模型的警告阈值。对于多组模型，可取所有警告阈值的平均值。

3.数值实验

为验证本文所提模型的有效性，本节将其应用于实际数据中，并与文献[3]所提动态基线模型比较。

a) 数据预处理

本次实验以个人网银业务为对象，对其业务流量数据进行采集和处理。首先对原始数据进行预处理。为使基线值预测更准确，这里将工作日的数据与周末数据区分开。对于缺失数据，由于可以认为数据在同一节点上的数值分布基本一致，因此从横向角度，将某一天固定节点处的缺失值用前若干天相邻节点值均值进行填充。若前若干天数据有缺失，则对该天数据发掘纵向分布规律，根据分布填补缺失值。

根据数据特点，我们对原始数据选取两个代表性特征，即交易量和平均响应时间。其次，考虑到这两个特征的量纲级别差异较大，因此进行最大最小标准化，将特征归一到[0，1]区间。对于ml个数据样本集，第i个样本点zi标准化后的点记为ri，则

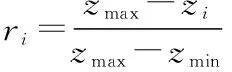
这里，zmax和zmin分别是该特征数据的最大值和最小值。类似地，可以对每个指标(共n个)分别进行同样的标准化。本文中，不妨记标准化的数据仍为T={xij}。

b) 参数选取

在实际中，本文所提算法中LS-SVR模型若固定参数值会降低模型性能。因此，最优训练天数及模型中参数需进行选取最优值。由于采取全天节点同时预测，而又可以认为同一节点数据分布基本一致，因此这里只考虑线性回归，从而模型只需考虑优参数C及最优训练天数。

对于训练天数的选取，当天数过少时，将导致预测结果很不稳定；当天数过多时，由于数据流量具有时效性，因此较早数据已不具参考价值，从而将影响预测结果。综合以上分析及数值实验，以绝对误差为检验标准，我们选取7天为实际训练天数。

当选择模型(2)的参数C时我们采取网格搜索法。首先，根据经验，确定两参数的范围为{2-8，2-7，…，27，28}。在此范围内，对惩罚参数寻优。

c) 动态基线值预测

文献[3]中利用线性加权技术，使得新一天基线值由先前基线值及若干天真实值的加权而得到。文章中指出，基于加权方法的动态基线效果优于固定基线。因此，下面将本文所提基于LS-SVR的动态基线预测与该加权基线预测方法进行比较。

图1(a)、(b)分别给出了两个不同时间段各节点处的真实值，以及基于加权方法和基于LS-SVR方法所得到的动态基线值。图中红色虚线代表真实值，蓝色实线代表两种方法预测所得的基线值，且(a)、(b)图中左侧子图均为文献[3]中基于加权方法预测的基线值，右侧子图为基于加权方法预测的动态基线值。从图中可以看出，无论哪个时间段，基于加权方法所得基线值均与真实值相差较大，而本文所提算法则更接近真实值，同时更符合真实数据的曲线趋势。实验结果表明了本文所提算法的有效性。

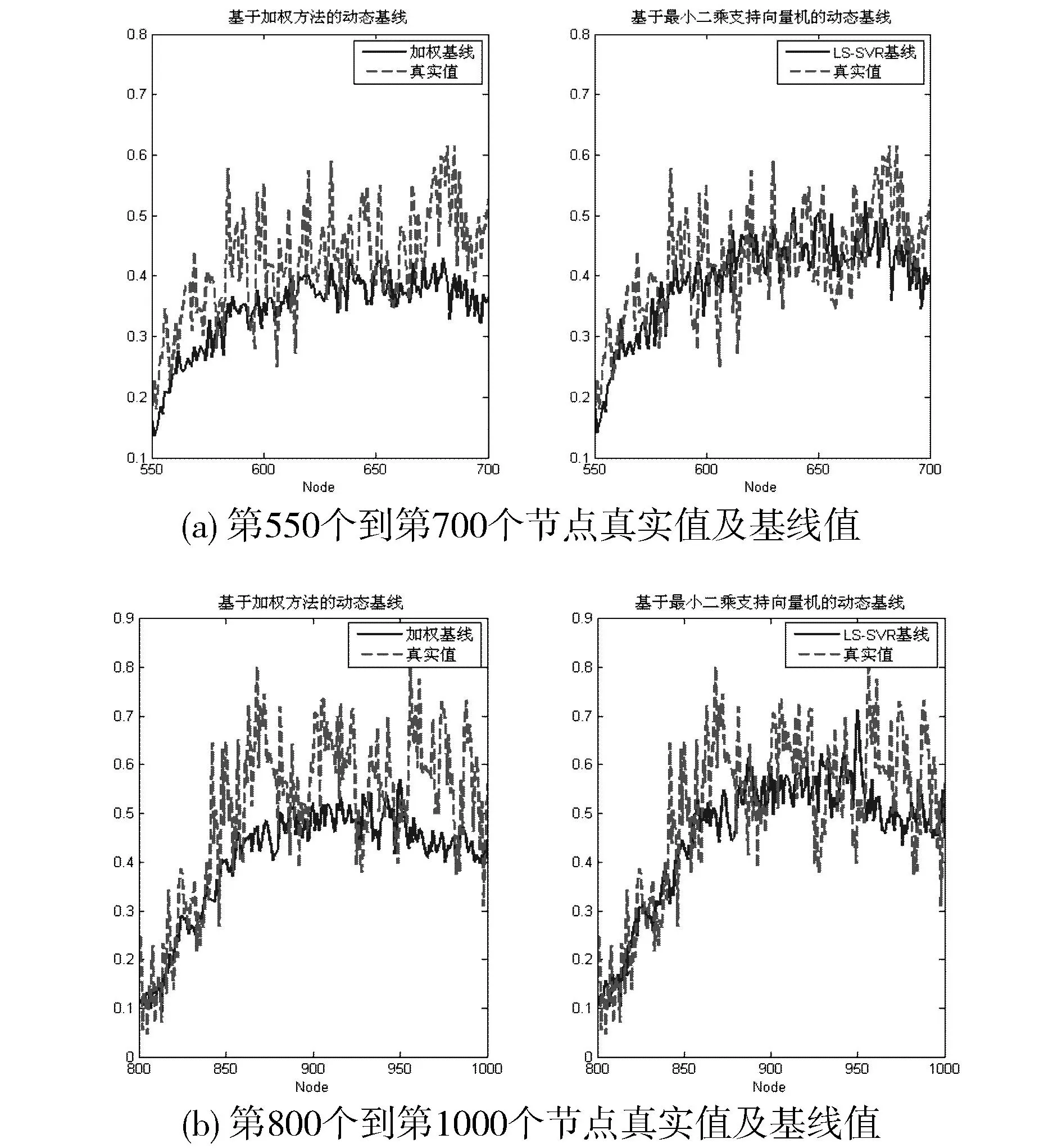
图1 不同时间段节点处真实值及基于加权方法、基于LS-SVR方法的动态基线值

d) 预警阈值确定

本节首先采用绝对对误差p为确定阈值的指标：p=|xi,l+1-yi|，其中xi,l+1为预测天的真实值，yi为得到的拟合基线值。

在数据处理过程中提取判断指标的数据，可以得到各天的判断指标误差分布。由于假设已知数据皆为真实且无异常的数据，因此可以根据误差分布图对阈值进行确定。我们将判断指标数值归一到0～1的范围内，如图2所示。

因为在没有噪声的情况下假设所有数据均正常，因此不应有警报，此时警告程度应为0。在加入白噪声且强度为最低的情况下，应有警报产生，由此符合警报的敏感性。由于噪声强度为最低，所以不应该有非常大的差异。此外，当添加强度为1的噪声时，警报应该比添加低强度噪声时更敏感，且应有较大差异。

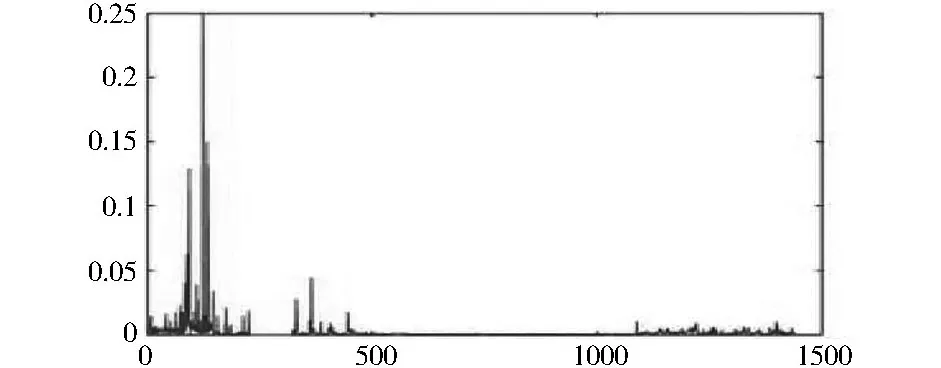
图2 某日判断指标归一化后的分布

基于以上思想，分别加入白噪声强度为0和强度为1的白噪声，并如上处理方式，可得此时的判断指标如图2所示：

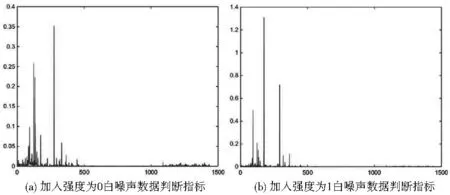
图3 加入白噪声数据判断指标图

结合图2及图3的数据指标分布可以确定：阈值的判断指标为小于0.26为正常；大于等于0.26且小于0.36为轻微警告；大于等于0.36且小于0.56为中级警告；大于等于0.56为严重警告，具体如表1所示。

表1 基于相对误差的警告阈值确定表

4.结论

本文提出一种基于机器学习的新的动态基线方法。通过结合无监督降维技术及基于最小二乘支持向量机的回归技术，本文构造了新的确定动态基线的方法。该方法能实现对每天各个结点的实时预测，并确定实时基线。实验表明，该方法较基于加权方法的动态基线有很大优势。

[1] Jolliffe I. Principal component analysis[M]. John Wiley & Sons，Ltd，2002.

[2] Van Gestel T，De Brabanter J，De Moor B，et al. Least squares support vector machines[M]. Singapore: World Scientific，2002.

[3] 郭炜. 基于动态基线的业务运营支撑网异常流量检测研究[C]. 中国通信学会学术年会，2011.