沪市股指收益率预测—基于ARCH模型

杨翻翻

(广西民族大学，广西 南宁 530001)



沪市股指收益率预测—基于ARCH模型

杨翻翻

(广西民族大学，广西 南宁 530001)

我国股票市场存在着制度不健全，投资者投资理性程度低、投机性强，市场受政府政策影响大，股票价格经常有大波动等问题。本文选取了2012年6月1日至2015年5月22日的上证综合指数作为样本，探究中国沪市股指波动的动态特征，并运用GARCH(1，1)模型对5月22日之后的沪市股指收益率走势进行预测。实证分析显示，沪市股指具有杠杆效应、波动表现出集群性和持续性。最后，本文根据我国沪市股指的波动特征，提出了相应的应对措施和建议。

ARCH效应；GARCH模型；沪市股指；收益率预测

一、引言

(一)研究背景与意义

股票的价格波动对投资者的经济利益有着直接的影响。由于我国股票市场的信息不对称，投资者极易受到其他投资个体的影响，从众进行投资[1]。当投资者对相同的股票进行大量交易时，容易导致股票价格剧烈波动，股票价格不能真实反映资产的价值，从而容易引发金融危机。

由于中小投资者获取有效信息的能力有限，其投资决策行为容易被庄家影响，因此，出于维护这一弱势群体的经济利益，中国证监会也出台了一系列政策以维护市场稳定。在中国这种新兴的资本市场及各种新政策环境影响下，正确认识股指收益率的波动特征，使用有效的模型对股指收益率序列进行拟合并给出正确的预测，这不管在是在引导投资者进行理性投资，还是在维护中国金融市场安全，促使我国股票市场尽快走向成熟资本市场发展方面，都具有重要的意义，因而这也是股市成立以来学者们重点研究的原因。

经典线性回归模型中假定随机误差项μ是同方差的，但是对于金融时间序列尤其是高频数据而言，往往会表现出明显的集群现象，而一般的宏观经济变量如GDP的增长率却没有这种聚类现象。因此高频金融时间序列数据建模后的残差具有异方差特性和自相关性，这种特征被称为“ARCH”效应。自回归条件异方差ARCH模型假定随机误差项的条件方差与其误差项滞后的平方有关，能较好地描述金融时间序列的ARCH效应[2]。因此，ARCH模型被广泛应用于股价和汇率的波动性研究和预测方面。而GARCH模型的提出是为了分析证券市场时间序列的规律性波动，它能非常好的拟合金融数据的波动性。

本文运用ARCH模型及GARCH模型对2012年6月1日至2015年5月22日上证综合指数的波动进行分析，解析我国沪市股价的波动特征，旨在为我国中小投资者理性投资、规避风险提供科学的决策依据。

(二)文献综述

对于投资者来说，证券市场收益高的同时风险也很高，因而正确认识股市的价格波动特征，并据以选择对应的模型来对股市进行模拟及预测，为广大投资者及管理者提供有力的工具，是目前研究的热点问题。

国际方面，Engle(1982年)提出了ARCH(p)模型，由于该模型能很好地拟合具有尖峰厚尾特性的金融数据，因而为解决股票市场价格存在的自回归条件异方差问题提供了解决的工具[3]。然而，后来有学者研究发现，有些时间序列只有在p很大时ARCH模型才能较好的拟合条件方差，因此，Bollerslev(1986年) 提出了GARCH模型，该模型是在ARCH模型的基础上加入了带有滞后期的条件方差误差项[4]。由于GARCH模型能够有效解决样本较少条件下模型阶数过大导致的计算效率以及精度低问题，处理厚尾能力强，能够更加有效地描述条件异方差的动态特征，因而备受业界人士的青睐[5]。

近年来，随着ARCH和GARCH模型在时间序列模型中的广泛应用，我国很多学者也就中国股市使用时间序列模型进行了诸多相关的研究：

王玉荣(2002年)用ARCH模型拟合深沪两市的股票收益率序列，实验结果表明，我国股市的波动具有群集性和非对称性，但高风险与高回报并未成正相关关系[6]。谷岭针(2009年)等学者运用GARCH模型对沪市收益率序列进行实证分析，得出沪市波动具有杠杆效应，ARCH模型能很好的拟合沪市收益率波动性的结论。

综合上述国内外学者对ARCH模型和GARCH模型在金融时间序列的预测方面的研究发现，已有研究不是运用ARCH模型和GARCH模型对数据进行建模，就是比较模型参数估计方法，而还未有人把两者联系起来对股市进行预测分析。因此，本文将在前人研究的基础上将ARCH模型与GARCH模型的建模和参数估计方法联系起来进行比较研究，以期得到一个较好的股市预测模型。

二、理论模型概述

(一)ARCH模型

传统的回归模型在古典假设中要求扰动项具备同方差性，然而在实践中该要求通常难以得到满足，扰动通常表现出异方差性，尤其是在金融时间序列中，常常会表现出波动的集群性。ARCH模型误差项在该时刻的方差依赖于上一时刻残差平方的大小[7]。因此，ARCH模型由原始的回归模型和方差的回归即均值方程和方差方程构成：

(1)

(2)

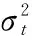
(二)GARCH(p，q)模型

广义自回归条件异方差GARCH(p，q)模型由(1)式和下式构成：

(3)

其中，p≥0，q>0，α0>0，αi≥0(i=1，2，……，q)，βj≥0(j=1，2，……，p)。

当q=0时，GARCH(p，q)模型就是ARCH(p)模型的特例，此时GARCH(p，q)模型可以像ARCH(p)模型一样模拟价格波动的集群现象。GARCH是ARCH的无限阶过程，因此，在计算量较小时，GARCH模型能更准确地描述高阶的ARCH过程。

当样本量足够大时，GARCH(1，1)模型就已足够拟合方差的动态特征，而且样本数据序列频率越高，检测到的ARCH效应就越显著。

GARCH(1，1)模型，其形式由(1)式和下式构成：

(4)

GARCH(1，1)模型与ARCH模型的区别在于GARCH(1，1)模型的方差方程中多了一个σ2，即条件方差GARCH项，该项在条件方差方程中的加入可以减少对很多参数的估计。

因此，本文在对上证指数的ARCH效应检验的基础上，运用GARCH(1，1)模型来建模预测上证指数的走势。

三、实证分析

(一)数据选取及处理

本文选用2012年6月1日至2015年5月22日，共726个交易日的上证综合指数数据序列来探究沪市的波动性。为减少舍入误差，在估计时，对上证综合指数的每日收益率Rt以相邻营业日股指对数的一阶差分表示，即Rt=logPt-logPt-1，t=1，2，3，…，726，使用软件Eviews5.0对其进行分析。

(二)OLS自回归和统计特征

对上证综合指数日收益率序列Rt进行OLS自回归，方程残差如图1所示：

图1 上证综合指数收益率残差图

图1中，上证综合指数收益率在以0为中心，振幅为±0.8之间频繁波动。对数收益率波动表现出时变性、突发性和集群性现象；具体表现为2013年上半年，2014年9—12月，2015年2—5月收益率波动非常大，2012年下半年及2014年1—8月波动非常小，波动的成群现象表明了误差项可能存在条件异方差性。

图2 上证指数收益率的统计特征

图2及表1说明了上证指数收益率序列具有尖峰和厚尾的特征，从标准差可以看出其波动性比较大。而Jarque-Bera正太检验结果为671.5979，因此，拒绝该对数收益率服从正态分布的假设。

(三)ADF单位根检验

对上证指数收益率序列的平稳性进行检验，检验结果如下：

表1 ADF检验结果

如表一所示，t值为-12.5，对应P值接近于0，在1百分之一显著水平下的MacKinnon值为-3.970846，表明至少在99%的置信水平下拒绝原假设，故可认为收益序列不存在单位根，说明该上证指数收益率序列是平稳的。

(四)ARCH效应检验

由以上OLS自回归和ADF检验结果可见，上证综合指数收益率序列ln?[R_t]具有时变方差性，且不符合正态分布，因此得对该序列进行ARCH效应检验。

对上证综合指数收益率数据进行去均值化并取平方处理，得到残差的平方，结果如下图所示：

表2 上证指数收益率残差平方自相关和偏相关图

从表2可以看出，上证指数收益率序列残差的自相关系数和偏相关系数不为0，且几乎所有的Q统计量都非常显著，所以沪市收益率序列存在ARCH效应。

(五)模型估计

1、GARCH模型估计

用GARCH(1，1)模型对上证综合指数收益率序列进行重新估计，结果如表3所示。

表3 GARCH(1，1)模型估计结果

由表3可以看出，ARCH和GARCH项都通过了1%的显著性水平检验，且ARCH和GARCH系数之和大于1，但该值离1并不远，说明波动具有持续性。因此，上证综合指数收益率序列存在着明显的ARCH效应。

继续对该方程进行条件异方差的ARCH-LM检验，在滞后阶数p=1时的情况如下：

表4 GARCH(1，1)模型ARCH-LM检验

由表4可见，因为P值为0.067大于0.05，F统计量均不显著，说明利用GARCH模型消除了原残差序列的异方差效应。因此，得到GARCH模型的均值方程和方差方程如下：

(5)

(6)

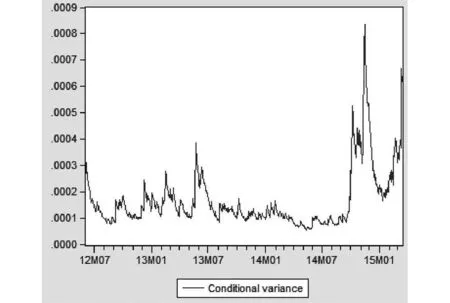
图3 条件方差图

由图3可以看出，上证综合指数收益率的波动具有持久性，而不是像残差序列一样频繁的跳跃式波动。2012年6月至2014年7月之前上证指数收益率的波动维持较低位水平，表明此段时间中国A股风险水平很低；而从2014年9月开始上证指数收益率的波动率开始迅速上升，其中2014年12月的波动率达到了高峰，表明此段时间中国A股投资风险很大。

四、结论与建议

通过对上证综合指数波动的实证分析，可以看出上证综合指数存在着明显的ARCH效应，并且GARCH(1，1)模型能很好地拟合上证综合指数收益率序列的波动情况。根据对上证综合指数的实证分析，可得到如下结果：

1、沪市波动具有集群性

α_1均为正，表明股价波动具有集群现象，实证结果也进一步证实了中国股市波动幅度大、频率高、ARCH效应明显等特征。

2、沪市波动具有持续性

我国股票市场受政府严格管制。当股市暴涨或暴跌时，为了维护企业和投资者得利益，政府通常会出台相应的政策干预股市，使股价波动维持在政府预期范围之内，因而波动持续性较短。由于GARCH模型中系数和大于1，说明波动具有持久性，所以，当前信息对预测未来股价波动影响很大。

3、沪市具有杠杆效应

由于股票市场的信息不对称，沪市股指收益率的波动存在杠杆效应。大盘上涨时，大股民均看好未来股市收益，从而选择大规模进场，进而促使股市行情持续上涨；而当大盘下跌时，投资者会越跌越看跌，越来越慌张，纷纷抛售，导致股市下跌势头更猛，最终股市持续下跌。

沪市Rt序列的GARCH模型中值均为正，但t统计值不显著，说明沪市的收益和波动变化之间的关系不明显，这主要是由于我国政府经常干预股市。同时也说明我国股民往往是风险喜好者，我国股市参与者投机性较强，上海股市具有较强的投机性。

我国股市自成立二十多年以来，虽然非常快，但股市相关的规章制度还并不完善，尚属新兴市场，还有诸多地方需要不断完善、规范。我国投资者由于信息不对称及自身收集信息能力限制等原因，在进行股票投资时极易受到他人的干扰和影响。因此，为了我国股市能够尽快走上正轨，投资者能够理性进行投资，本文提出以下两点建议：

首先，认识上海股市的波动特征，并据以建立可靠的股市走势预测模型，为广大投资者规避风险提供决策工具，为管理部门对股市实施监管提供决策依据。

其次，中国股市受政府管理部门管制，股市经常受到政策冲击。因此，管理部门应当出台相应的政策，尽量消除消息不对称现象，使广大中小投资者更好地掌握股市情况，理性进行投资。

[1] 姚战琪. 基于ARCH模型的我国股票市场收益波动性研究[J]. 贵州财经大学学报，2012，30(4):52-57.

[2] 袁霓.国内油价市场波动的ARCH模型分析[J].技术经济与管理研究，2009(1).

[3] 金成晓，曹阳. 基于非参数ARCH模型的沪深指数波动性研究[J]. 山西大学学报(哲学社会科学版)，2014，37(3).

[4] 王敏，张萍.初探中国沪市股价波动性——基于 ARCH模型和 GARCH模型[J].科技创业月刊，2010(1).

[5] 邓传军，刘家悦，李轩. 沪市股票收益率的ARCH模型分析[J].当代经济，2007(11).

[6] 庄彬惠，曾五一. 股票市场波动预测的ARCH族模型选择[J]. 统计与信息论坛，2006，21(4):48-52.

[7] 李嫣怡、刘荣等.Eviews统计分析与应用[M].北京：电子工业出版社，2013.本文获广西自治区级协同创新中心(培育)项目“广西沿边沿海经济开放发展协同创新中心”的资助(113000100650006)。