电子商务环境下基于点击流的需求预测模型和企业库存优化
2016-12-14许圣佳
许圣佳 蒋 炜
(上海交通大学安泰经济与管理学院,上海 200030)
电子商务环境下基于点击流的需求预测模型和企业库存优化
许圣佳 蒋 炜
(上海交通大学安泰经济与管理学院,上海 200030)
基于电子商务平台中较有代表性的两大数据:点击量和购买量数据之间的关系,通过点击量和购买量的历史信息进行需求预测,并对需求预测模型的有效性进行理论证明。以电商企业为研究对象,以库存成本最小化为目标,运用单阶段报童模型对电子商务企业的库存模型进行优化,证明模型的有效性、适用条件及其库存成本降低的概率下限,分析适用于这一优化模型的企业特征,并为企业提出相应的库存策略。基于天猫平台实际数据,对加入需求预测模型的报童模型的性质进行了实证研究。结果表明,并非所有电商企业都能通过应用点击-购买需求模型对库存管理进行优化,电商企业应根据企业自身特征采用相应的库存策略以降低其库存成本。
电子商务;需求预测;库存模型
1 问题描述及假设
大数据时代下,互联网引入了由用户产生数据的模式,并伴随着数据多源头、低成本和更及时的特征。与此同时,互联网相关技术的革新使得数据的收集和分析成为可能。构建在互联网基础上的电子商务和传统零售比较的优势之一就是数据的可获得性。电子商务可以实时获取顾客的访问源头,在网站内的点击、搜索、收藏、购买等行为,以及购买商品间的关联性。这些数据既可以帮助企业更精准地服务于顾客,也为企业提高供应链管理效率、降低库存成本提供了机遇,同时也向企业提出了两个问题:首先,怎样将海量数据真正应用到库存模型的优化中?其次,面对拥有不同核心关切点的企业,优化的库存模型是否适用于所有企业?
本文的库存情境设定为单一阶段的库存问题(single-period problem,SPP)也称为报童模型,是用于单一阶段中寻找能使利润最大化的订货量的模型。SPP模型假设,如果在一个阶段结束时有任何多余库存都会被折价销售或直接废弃处置,产生的成本称为持有成本;如果订购的量小于实际的需求,则报童损失一些利润,产生的成本称为缺货成本。SPP模型反映了许多生活实际情况,经常被用于生产和零售阶段以决策最优订货量。对这一问题的研究从许多方面进行延伸,包括处理不同的目标函数和效用函数,不同的供应商定价策略,不同的报童定价策略和折扣类型,不同的关于需求信息的状态,以及多种产品相关的问题。本文着重关注对于不同需求信息状态的延伸问题,将如何把需求预测信息结合到库存管理决策中为研究重点。Fisher和Raman考虑了一个二阶段的报童模型情况,这是一个多产品生产的问题,其中引入了在每个时间段之间更新预测以及对第二阶段容量进行约束的问题。Eppen and Iyer提出了一个负责的订货启发式算法,来解决信息更新,对一系列需求分布的多阶段模型。有许多文献考虑了信息更新对一个供应链设计中的订货策略产生的影响。
经典的报童问题中通常有以下假设,也是本文模型建立部分的假设说明:
Q——订货量;
Q*——最优订货量;
h——单位持有成本;
b——单位缺货成本;
D——需求;
Xt-1——第t-1天的点击量;
F(·)——随机需求服从的累积分布函数;
f(·)——随机需求服从的概率密度函数。
2 模型建立
2.1 需求模型建立
在关于SPP问题的扩展研究中,顾客需求是一大亮点,它不仅将运营管理结合市场营销、统计学等进行跨学科的融合,还能使得SPP问题更贴近实际。通常,在以往的分析中,顾客需求是作为一个外部参数来处理的,但是在不同环境下,可能会出现一些与内部参数相关联的情况,例如顾客需求和价格相关联,顾客需求可能受到市场营销以及被买家扩大的效应所影响,又或者顾客需求可能会被买家的存货所影响。在经典的报童模型问题中,销售价格被认为是外生的因素,也就是零售商对其无法控制的。这在一个完全竞争市场,即买家是完全的价格接收者来说是正确的。然而在实际情况中,零售商可以调整现有的价格以增加或减少需求。本文更关注的是市场营销(market effort)对顾客需求的影响情况,因为这是直接与企业对策相关联、并结合运营管理和市场营销的问题。客户需求经常会被一系列市场活动所影响(例如,广告,销售电话,或是商店内的展示等等)。而对于电子商务平台上的企业来说,点击量是顾客流量的一个直观的指标,它与企业的营销、运营环节都有着密不可分的关系。
本文首先建立两种不同的需求预测模型。传统研究中通常假设第t的需求Dt为:
Dt=μ1+σ1Z
其中Z为标准正态分布的随机数。当我们可以观察到前一天点击量时,对当天的需求预测方法进行了转变,即:其中是点击量和购买量之间的相关系数。

通过建立需求模型,我们可以得到:
性质1 当β≠0时,基于点击-购买相关性的需求预测模型的预测误差减小。
证明:由
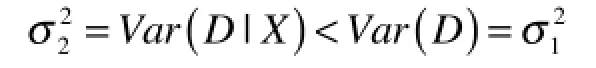
因此点击-购买需求预测模型减小了预测误差。
2.2 库存模型建立
本文根据第2部分假设,建立单阶段的报童模型,以成本最小化为优化目标,则目标函数为:

对期望成本关于订货量Q进行求导可得:
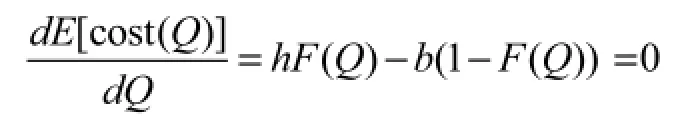

令Φ(z)=Pr(Z≤z)为标准正态分布的累积分布函数,令由此可以得出,。又因为:
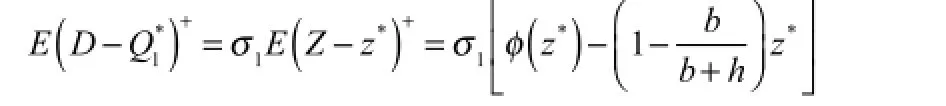
其中φ是标准正态分布的概率密度函数。结果可得,在最优订货量为Q1*时的期望成本为:
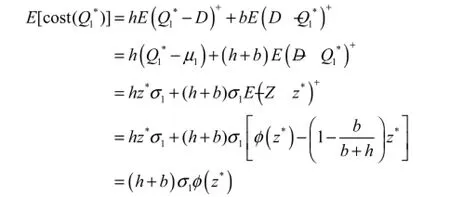
这一结论表明,最优订货量下的库存成本只与需求预测误差的方差有关,也就是说,需求预测越精准,库存成本越小。因此,我们得到了性质2。
性质2 基于点击-购买需求预测模型下的期望库存成本降低。
证明:根据式(1)可以得到:Q2=μ2+σ2Z。假设β1≠0,通过性质1我们已经证明了,即通过点击量信息使得需求量预测更为精准,从而减小了预测误差的方差。因此可以证明:
可
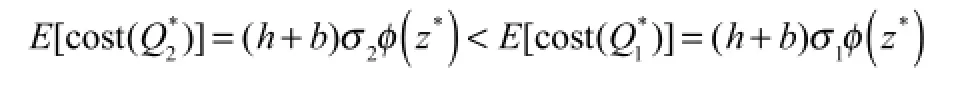
从上述证明中,我们可以得出,在单一阶段报童模型下,期望成本的大小只与需求预测的准确度有关。通过探索需求与点击量的关系,提高了需求的预测精度,从而能从理论上证明,库存的期望成本得以降低。
我们运用前92天的数据作为训练集,对后31天的数据进行测试。选取较为活跃的品牌(ID:7868)进行实证检验,在检验中随机假设了单位缺货成本和单位持有成本的结果如下图所示:
可知,两种需求预测模型下的订货量的差值
为:(2)当
时,即(2)式≥0时;i. 当
时,
可得,
ii. 当
时, ,则无法确定成本之差的正负性。
iii. 当
可得,
时,时,即(2)式<0时;iv. 当
可得,
。
同样地,当
时,
图1 某品牌(ID:7868)的31天内库存成本比较
图1中横坐标代表测试的某一天,纵坐标表示当天在不同需求预测模型下的实际库存成本之差,实际库存成本的计算方法如下:
可得,
v. 当
时, ,则无法确定成本之差的正负性。
vi. 当
可得,
时,
可得,
。
将上述六种情况进行汇总,结论如下表所示:
从图1中可以看出,在改进的需求预测模型下,并非每天的库存成本情况都有所改善,虚线以下部分代表了品牌在应用点击-购买需求预测模型后,库存成本没有减少反而增加。这就带给我们一个疑问,大数据最为推崇的理念中有一个就是掌握相关关系,而非因果关系,然而,是否所有电商企业都能运用大数据理念下的优化方法呢?正如前文所提到的,电商企业的库存管理问题是电商企业能否良好运营的一大要素,能直接关系到企业的生存问题。仅看期望库存成本降低是远不够的,更应去探索运用模型的适用条件,从而使企业做出更精准的库存订货策略。
为探索运用点击-购买需求预测模型对库存进行优化的适用条件,首先要确定当天需求与订货量之间的关系。我们已经知道:
从表格中可以得出结论:
(1)当
时,库存成本得以减小的条件为:
因此,当给定Xt-1时
。
(2)当的情况下库存成本会减小,以此判断电商企业应用点击-购买需求模型来降低库存成本的适用条件。
条件中,
时,只有在当天需求
由上文中已求出的
可得出:是已知的,并只与假设已知的单位持有成本、单位缺货成本以及需求预测模型预测准确程度(即σ1,σ2)有关,因此可以在决策前判定
性质3 根据在不同需求预测模型下当天补货量的大小,可以得到库存成本减小的概率下限为:
(1)当传统需求预测模型下的补货量大于(等于)点击-购买需求预测下的补货量时,库存成本减小的概率下限为的大小关系。然而,我们对当天的真实需求Dt的大小是未知的,因此应对Dt和适用条件值之间的关系进行概率的研究。
①当
时,
。
(2)当传统需求预测模型下的补货量小于点击-购买需求预测下的补货量时,库存成本减小的概率下限为
。
其中,b和h分别代表单位库存的缺货成本和持有成本。
根据性质3中所示,当单位缺货成本大于单位持有成本时,即 (3)已知条件①下, ,将Q(1)*,Q(2)*的表达代入可得:μ1+σ1z*≥μ2+σ2z*,进行一定的变换后可以得到,h(μ1-μ2)≥(σ2z*-σ1z*)。将这一条件代入(3)式得到:
②相似的,当
时, ,此时若计算得到传统需求预测模型下的订货量大于(等于)基于点击-购买需求预测模型下的订货量的话,则库存成本降低的概率大于50%,可以考虑利用点击-购买需求预测模型来降低库存。乍一看,似乎与我们的直觉不完全一致:因为当缺货的惩罚成本高于存货的持有成本时,我们可以理解为货多出来比不够卖要来得好,那么基于传统需求预测模型下的订货量更大时,其缺货的可能性应该比订货量更小的那种情况要小,可是数学推理出的结果却是库存成本降低的可能性大于50%,比订货量增加情况下的库存成本降低概率下限要更大。仔细分析则需要问一个问题,即什么时候订货量在点击-购买需求预测模型下会小于基于传统需求预测模型下的订货量呢?从两种需求预测方法下的订货量公式中我们可以得到:
当
时,
,的表达式代入可得:μ1+σ1z*<μ2+σ2z*,进行一定的变换后可以得到, (4)已知条件②下,
即:
,将。将这一条件代入(4)式得到:
也就是说,我们暂且不考虑点击-购买相关性为负的产品(即点击量越大,购买量反而越少的产品),假设点击量和购买量的相关系数,则当时,我们可以看到,不等式右边是在0到1 的范围内的,因此只有在前一天的点击量小于历史平均点击量/或右趋近历史平均点击量时,才会出现订货量减少的情况。这一点是符合直觉的,其本质也正是点击-购买需求预测模型的实质所在,即考虑前一天点击的情况来判断后一天购买的变化情况。因此,根据模型的隐含意义,当前一天点击量小于历史平均点击量时,应该相应地减少订货量,从而导致订货量小于传统需求预测模型下的订货量。这时,若预测是准确的话,当天的真实需求应该更接近于加入对前一天点击量考虑的预测需求,因此其缺货的可能性即便有,也未必非常大,即便真的缺货了,也不一定会出现实际需求大于传统需求预测模型下的订货量这种情况,否则前一天点击量减小的情况就难以解释了(因为至少点击量表现与历史平均点击量相比不太理想的情况下,购买量却远超历史平均量的情况并非合理或常见的状况)。所以,我们可以认为,当单位缺货成本大于单位持有成本时,首先,实际需求同时大于两种需求预测模型下订货量的情况是较为异常的,只有在这种情况下,库存成本在运用了点击-购买需求预测模型后不降反升;其次,对于实际需求在两种方法下的订货量之间的情况,则根据实际需求的偏离情况和缺货成本与持有成本之间的差值情况,有一定概率会使得库存成本在运用了点击-购买需求预测模型后降低;最后,当实际需求小于更小的订货量时,库存成本在运用了点击-购买需求预测模型后一定会降低。同时,当前一天的点击量小于历史平均点击量的差值越大,则根据概率计算的推导过程可以得出,库存成本降低的概率越大于性质3中的概率值下限,也就是说库存成本降低的概率越高。
类似的,当
时,
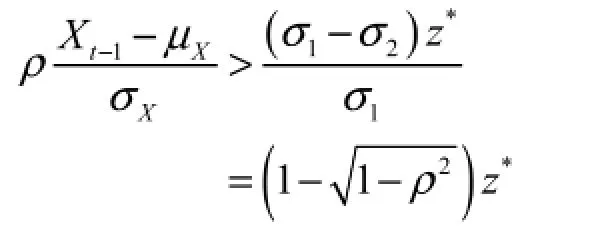
对应性质3的第(2)种情况,依旧延续上述的分析,当单位缺货成本大于单位持有成本时,也就是说,此时若计算得到传统需求预测模型下的订货量小于基于点击-购买需求预测模型下的订货量的话,则库存成本降低的概率的下限是小于50%的,当然,下限小于50%不代表电子商务企业不应该应用点击-购买需求预测模型来改善库存管理,而是要看订货量比传统需求预测模型下的订货量大多少。概率下限本身是一个决策的参考因素,但我们不能忽视的是产生这一概率的先决条件,即订货量的增加或减少,而订货量的增加或减少就反应出点击流信息在其中发挥的作用。依旧是假设单位缺货成本大于单位持有成本,初步看来库存成本降低的概率只是大于一个50%都不到的数字,看似充满了不确定性。然而,当基于点击-购买需求预测模型下的订货量远大于传统需求预测模型下的订货量时,根据上述公式推理可知,不等式右边恒大于0,因此如果这个产品的点击量正向影响购买量,即点击量和购买量的相关系数大于0时,前一天的点击量必须远大于历史点击量的均值,才能使得基于点击-购买需求预测模型下的订货量远大于传统需求预测模型下的订货量。
既然点击量远大于历史点击量的均值,点击量与购买量呈正相关的关系,那么针对这一信息及时更新订货量的举措显然是预防大量缺货情况发生的策略,而根据传统的需求预测方法并不能将最能反映出产品关注热度的信息——点击流信息加入订货策略的考量中。此时,昂贵的单位缺货成本使得基于传统需求预测方法的订货策略的库存成本更高,而基于点击-购买需求预测方法下的订货策略的库存成本降低概率更高。所以在这种情况下,库存成本降低的概率下限本身不能完全等同于订货策略,而是要结合实际情况再对订货量进行决策。
从上述对性质3的分析中,我们可以得出一个较为全面的分析视角,即考虑了点击量信息对购买量的影响,从而制定订货策略。可以看出,前一天点击量的不同情况会首先影响到订货量的差别,其次还会影响到由订货量不同导致的最终库存成本增加或减少的概率。因此,将这些因素综合考量,我们可以得出不同产品在前一天点击量表现不同情况下库存成本降低的概率。在这里,为了分析严谨,还需要对产品进行分类,毕竟在实际数据情况中也有点击量越多,购买量却越少的情况,从现实角度来看,这些产品可能是因为营销不得当,只赚了流量和人气而没赚到金钱,例如对产品降价促销的营销方法华而不实,获得了点击量的上升,真正购买的人却寥寥无几。尽管分析时我们将这部分产品的情况也做了概率计算和分析,但点击-购买的正相关性依然是大部分产品的情况,从而得到性质4:
性质4 某一产品库存成本减小的概率下限为:

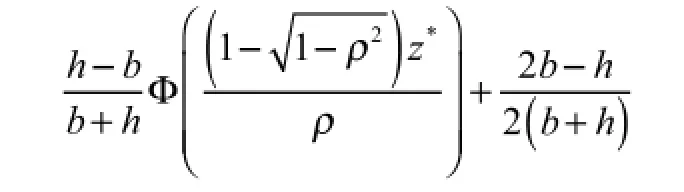
证明:由于不同品牌的点击-购买关系可正可负,当点击量越大购买量越大,即时:
根据性质3得到的在两种需求预测方法下导致传统需求预测模型下的订货量大于(等于)或小于基于点击-购买需求预测模型下的订货量,其库存成本降低的概率下限。我们对订货量何时会变大,何时会变小的概率进行计算,并整合成为总概率下限。又因为之前计算已得:不等式左边有关于点击量的标准正态分布的随机数形式,我们一如之前的计算设为Z,则可以将订货量增加或减小的情况看作是标准正太分布随机数Z的变动情况,具体证明过程如下:
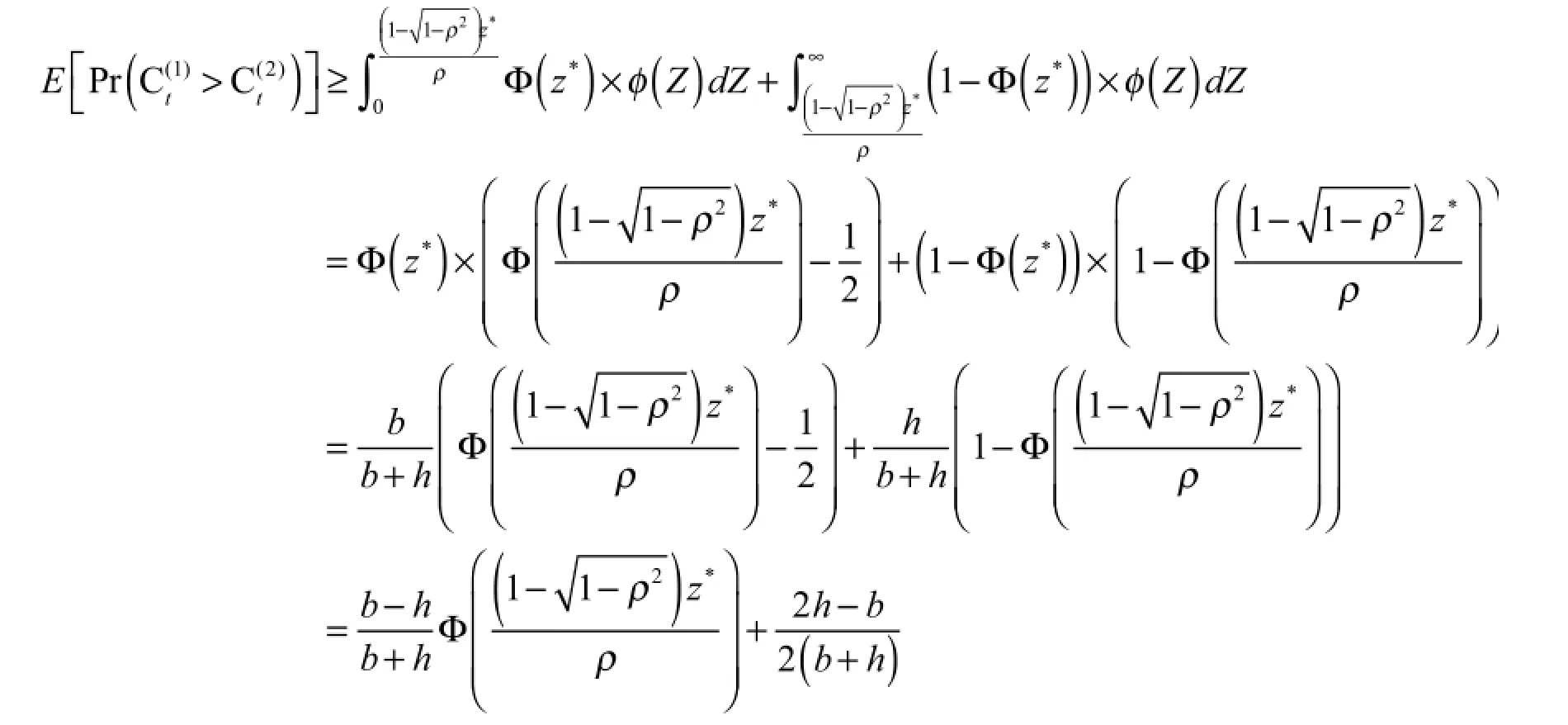
在单位缺货成本和单位持有成本给定的情况下,相关系数ρ越靠近1,即前一天的点击量与后时候甚至会适得其反,譬如说当相关系数十分小的时候,概率下限就会减少到预期外的值,更有可能使得库存不减反升。
而对于某一个品牌的产品来说,其相关系数是固定的,当相关系数固定时,可以看出概率下限这一值中,若单位缺货成本小于单位持有成本,或单位缺货成本大于两倍的单位持有成本时,都会使得概率下限式子中某一项为负。于是会产生的结果就是,如果单位缺货成本小于单位持有成本,则整个概率下限大小由单位持有成本主导,反之则由单位缺货成本主导。这样的设置有所偏颇和不合理之处。因此,在之后的实证部分,我们将单位缺货成本和单位持有成本的关系设定为:h<b<2h较为合理。
相似的,当某一产品的ρ<0时,经过点击-购买需求预测方法后的库存成本降低的概率下限为:一天的购买量正相关程度紧密,则越靠近(实证部分会进行单调性证明和数值检验),相关系数ρ越靠近0,则越靠近0.5。因此,随着前一天的点击量与后一天的购买量正相关程度紧密,库存成本降低的概率越高,这与我们的直觉也是相符的。同时也与本文撰写的初衷不谋而合,即要利用大数据进行精准预测与库存管理之前,应首先管理好小数据。大数据并非万能的解决方案,很多时候一味地套入大数据的概念不一定会得到好的管理结果,有

从表达式中可以看出,标准正态分布的累积分布函数中的代数式与ρ>0的情况下的代数式是一对符号相反、绝对值相等的数,但不影响这一式子的单调性。因此,当点击量与购买量的相关系数越接近-1,越接近于而
当相关系数越接近于0,则越接近于0.5。因此,即便是对于这一类特殊产品,点击量与购买量负相关时,也是当相关程度越紧密时,库存成本减小的概率越大。
3 实证研究
本文的实证部分运用阿里巴巴大数据竞赛(2014年第一赛季)所提供的数据(http://tianchi. aliyun.com/datalab/dataSet.htm?id=2),包含时长123天中,用户对品牌点击和购买的时间记录,其中用户和品牌都显示为加密ID,并无特征信息。在经过数据清理后,剔除了一些极度不活跃的品牌,例如在123天中只有点击从未购买,或购买次数极少的品牌,最后筛选出了442个独立品牌进行第二部分的模型验证。根据第2部分的阐述,我们着重对前一天的点击量正向影响后一天购买量的品牌(即ρ>0)的品牌进行研究,最后实证研究的样本为208个。将t-1前天的数据作为训练集,对第t天的数据进行测试比较。由于作为训练集的数据量要相对充分,因此将前92天作为训练数据集,即假设t≥93。
3.1 实证分析参数设计
本文的初衷是试图提出一种新的适合于电子商务企业的库存策略,这种库存策略的创新之处并非在于库存模型本身(例如报童模型)的创新和优化,本文突出的一点是利用了电子商务平台较为特殊的点击和购买的操作记录,及其操作之间的相关性来建立考虑了前一天点击量影响到购买需求。因此,最终想比较的基于传统需求预测模型下所产生的库存成本(,图中简写为C1,下同)和加入点击-购买需求预测后库存成本(,图中简写为C2)之间的差值(C1-C2)。然而,本文想要探寻的另一个问题是,在我们加入了更多信息来帮助决策后,是不是情况真的得到改善了呢?于是我们去探求了使用不同策略的适用条件,以及这一条件下库存成本是会上升还是降低的变化情况。在第二部分不考虑缺货成本的情况下,可以得出确定的适用条件,即只要满足了这一条件就能使库存成本降低。而在考虑了缺货成本的情况下,问题变得更加复杂,不仅需要考虑产品的特性,还应考虑应用了点击-购买需求预测模型后,库存成本降低的概率。因此,实证研究也将围绕这两个问题展开分析。
根据上述文中所分析的情况,我们假设单位缺货成本b和单位库存成本h的关系为:h<b<2h。
3.2 点击量对库存成本降低概率下限的影响
根据性质3中所提到的,前一天点击量不仅会影响到后一天最优订货量的大小,还因为基于传统需求预测模型下的订货量和基于点击-购买需求预测模型下的订货量的大小关系,而影响最终库存成本降低的概率下限。针对性质3,我们对208个点击-购买相关性为正的独立品牌进行实证研究,分别计算了在不同需求预测方法下的最优订货量,Q1和Q2(图中分别简写为Q1,Q2),以及两个最优订货量的大小比较情况,Q1-Q2(图中简写为Q1-Q2)。另一方面,实证研究将最优订货量结合真实实现的需求情况,比较基于传统需求预测方法的库存成本和基于点击-购买需求预测方法的库存成本孰大孰小。由于模型是建立在单阶段的情况下,所以我们每次比较的都是T+1的库存成本变化情况。并且,在测试集第93天到第123天这31天内,每次决策都充分利用了所有的历史信息即前t-1天的历史信息(包括点击量、购买量及两者的关系)。在对库存成本降低概率下限进行实证研究时,本文将对每一个品牌单独算出其降低库存成本的概率,即把31天的测试集中,库存成本降低的天数比上总天数来作为其概率,并完成两方面的实证分析:(1)验证模型理论值是否在实际数据的检验下正确合理;(2)在假设的单位缺货成本和单位持有成本的关系下,两种策略下的最优订货量导致的库存成本降低的下限是否和理论分析一致。

图2 订货量大小与库存成本概率下限分析
图2 中显示了在性质3的两种情况下实际库存成本降低的概率,分别如两个箱线图所示。每个箱线图中共有208个品牌库存成本降低概率的数据,每个数据又由独立品牌自身在31天测试集中的库存概率降低情况在订货量大小变化情况下的结果。例如第一个箱线图最底部那个十字星的异常点,就代表了208个独立品牌中有一个品牌在31天中,当Q1≥Q2时,库存成本降低的概率为33%左右,低于其他所有产品。接下来,我们根据上文中提到的两个实证研究方向进行考察。首先,本次实证研究对单位缺货成本和单位持有成本的数值假设为:b=38,h=20,符合h<b<2h的假设。因此,根据性质3,我们可以得到当传统需求预测模型下的补货量大于(等于)点击-购买需求预测下的补货量时,库存成本减小的概率下限约为0.6552。当传统需求预测模型下的补货量小于点击-购买需求预测下的补货量时,库存成本减小的概率下限约为0.3448。从图中容易看出,当Q1≥Q2时,四分之一分位超过60%接近70%,在允许存在一定随机误差的情况下,满足性质3中的第(1)种情况;而当Q1< Q2时,大部分样本都能满足库存成本降低概率大于0.3448这一理论性质,其四分之一分位同样是超过60%接近70%,除了两个异常值之外,基本都符合概率下限这一理论值,因此在允许存在一定随机误差的情况下,实证研究表明也满足性质3的第(2)种情况。
对于第二个实证研究问题,从图中可以清晰地看出,Q1≥Q2时相较于Q1< Q2时的箱线图下限明显上移,这也和我们性质3中表达的观点一致,并非说在单位缺货成本大于单位持有成本时,Q1≥Q2情况下库存成本降低的概率一定大于Q1< Q2时库存成本降低的概率,而是从避免库存成本不降反升的控制风险的角度来看,其库存成本降低的概率下限更高,也就是在最坏的情况下,要比Q1< Q2时的库存成本的情况好。可以看出,当Q1<Q2时,从四分之一分位开始的概率水平并没有太低,与Q1≥Q2情况下的概率水平相差不多,反而在顶部接近于100%的情况中占优。这是由于在点击-购买相关系数大于0的情况下,当Q1< Q2时,我们在第3部分已做过分析,必然是前一天的点击量大于或至少是略微左偏离于历史点击量均值的实际情况,这就说明了按照原来传统的需求预测模型,没有考虑到点击量这一个非常显著的指标,很有可能导致第二天缺货的状况,而在单位缺货成本远大于单位持有成本的时候,缺货的惩罚力度是很大的,也造成了库存成本在应用了点击-购买需求预测的策略后显著降低,因而对于一个品牌来说,当前一天点击量骤增时,选择应用点击-购买需求预测模型是十分明智的。
对于一个独立品牌来说,它本身的产品特性决定了其点击-购买相关系数的正负,我们在实证研究中着重分析点击量正向影响购买量的产品。要实证分析每个独立品牌的库存成本降低概率,我们将数据集的前92天作为训练集,后31天作为测试集,测试31天的测试天数中有多少天的库存成本得以降低,从而以库存成本降低率的形式体现出来。
如图3所示,箱线图的样本为208个独立品牌在31天测试集中,基于点击-购买需求预测模型对库存策略进行优化后库存成本降低的概率,具体概率的表达方式是通过计算31天中库存成本降低的天数除以31天得到的。图中纵坐标表示的是库存成本降低的概率(图中表示为:cost reduction probability)。每个品牌相互独立,其库存成本的降低概率与其他品牌无关。根据性质4,当产品的点击-购买相关系数ρ>0时,优化后的库存成本减小的概率下限为:

图3 208个品牌实际库存成本降低的概率

在实证研究中假设固定的b,h后,只和品牌本身的点击-购买相关系数有关。因此,我们需要证明库存成本减小的概率下限与点击-购买相关系数ρ之间的变化关系。
性质5 对于任意品牌,当点击-购买相关系数ρ越大时,基于点击-购买需求预测模型下的库存成本降低的概率下限越大。

对208个独立品牌就性质5进行实证研究,以第93天为例,考察每个品牌在前92天的训练集里的点击-购买相关系数和第93天库存成本是否降低的情况。并且,由于每个品牌的情况不同,为了使得库存成本比较的情况比较平滑,我们对库存成本进行对数化,结果如下图所示。
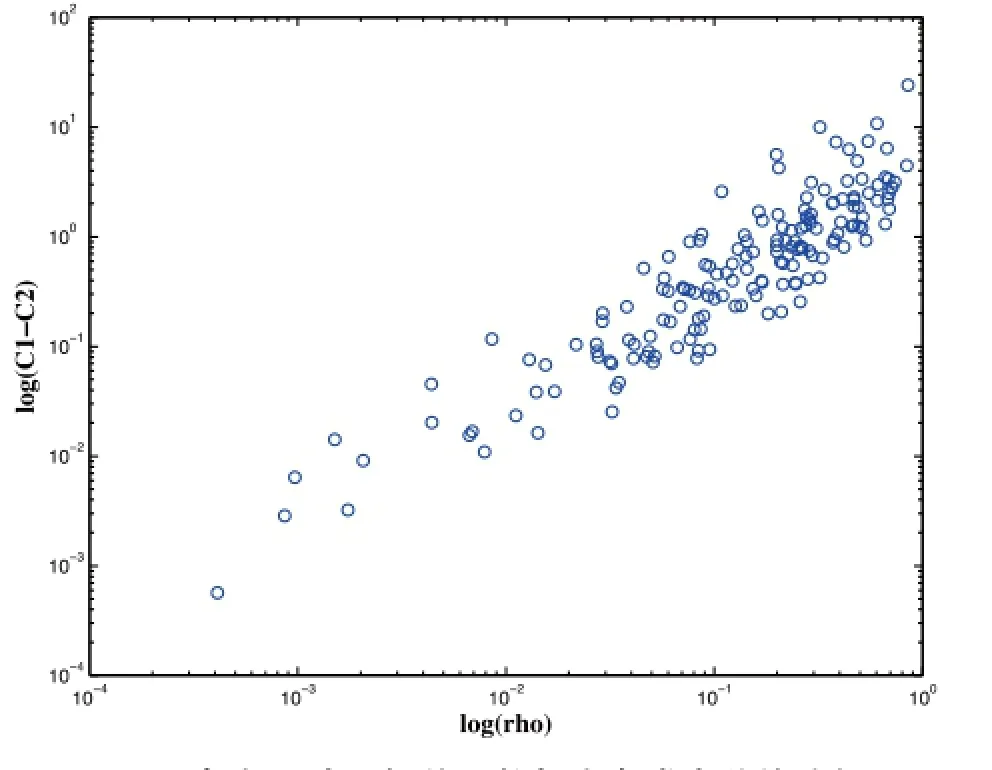
图4 点击-购买相关系数与库存成本差值分析
由于log scale下要忽略负值,为了使得可视化效果更好,我们只拿出了库存成本减小即图4中纵坐标(C1-C2)大于0的部分进行对数化,同时也对图中横坐标相关系数进行了对数化以拉开整个横坐标。从图中,我们可以非常明显地看到相关系数对库存成本降低的正向影响。就第93天而言,共有40个品牌的库存成本不降反升,其余168个品牌也就是上图中的样本,它们的库存成本都相应程度减小。这已然可以说明一定问题,虽然图式中的都是库存成本降低的品牌,但是随着点击-购买的相关系数变大,库存成本降低得更多,同样能说明相关系数对于减小库存成本有正向作用。这一点也与我们的直觉相符。
最后,我们将检验每个品牌库存成本降低的平均比例情况,对每个品牌在31天测试集中库存成本每天的降低比例(当小于0时,即成本不降反升),最后对31天的库存成本降低比例做平均,得到其库存成本降低的平均比例。结果如下:

图5 库存成本降低比例
可以看到大部分品牌的库存成本降低的平均比例都在0以上,集中在0到10%之间。经统计, 208个品牌中,库存成本平均降低比例大于0的有147个品牌,占总品牌数的70%,还有28个品牌的平均库存成本下降率达到20%以上。可以说,基于点击-购买需求预测模型下的库存成本降低比率也较为显著。
4 结束语
电子商务平台的海量数据是对用户行为和产品特征最直接和最真实的刻画,然而,试图运用大数据时代的解决方法来降低电子商务企业的库存成本、提高供应链效率,其应用本身应当包含适用条件。大数据作为一个技术为我们提供了许多人与人之间交互的数据和信息,但是真正的大数据并不是一些排名和信息的发布,而是从数据中理性找出内在的逻辑关系,并将这些逻辑关系应用于实践。如果不找到事物发展的规律而永远“闻数据起舞”的话,我们的决策往往会与期望相距甚远。每个电商企业将面临各自不同的优化需求,而优化模型反过来又将对企业的应用条件提出要求,若忽视了这种相辅相成的关系,将会出现与优化目标背道相驰的结果。本文将库存成本的减小作为企业库存管理的优化目标,对企业短期和长期的库存成本分别考量,最终提出模型的适用条件及分析方法,为电子商务企业的精准预测和库存管理提供决策支持。
[1] Nacif R C. Online Customer Loyalty: Forecasting the Repatronage Behavior of Online RetailCustomers[M]. Springer Science & Business Media, 2012.
[2] Kamakura W, Mela C F, Ansari A, et al. Choice models and customer relationship management[J].Marketing Letters, 2005,16(3-4):279-291.
[3] 武帅, 李双双, 陈毅文, 等. 网上消费者购物动机, 点击流行为及其之间的关系[C]//第十一届全国心理学学术会议论文摘要集. 2007.
[4] Sweiger M, Langston J, Lombard H, et al. Clickstream data warehousing[M]. John Wiley & Sons, Inc., 2002.
[5] Huang T, Van Mieghem J A. Clickstream data and inventory management: Model and empirical analysis[J]. Production and Operations Management, 2014, 23(3): 333-347.
[6] 黎客来, 汤震. 点击流数据仓库系统应用研究[J]. 计算机与现代化, 2008(2):53-56.
[7] Gunasekaran A, Marri H B, McGaughey R E, et al. E-commerce and its impact on operations management[J]. International journal of production economics, 2002,75(1):185-197.
[8] 曹文彬, 何建敏. 电子商务环境下基于合作预测的库存管理问题[J]. 中国管理科学, 2009(S1).
[9] 华东平, 钟麦英. 电子商务环境下的库存管理问题研究[J]. 东华大学学报: 自然科学版, 2002,28(3):20-24.
[10] 钟麦英, 汤兵勇. 电子商务环境下的库存控制问题研究[J]. 系统工程学报, 2002,17(3).
[11] Raman, A., M. Fisher. 1996. Reducing the cost of demand uncertaintythrough accurate response to early sales. Oper. Res. 44(4): 87–99.
[12] Eppen G D, Iyer A V. Improved fashion buying with Bayesian updates[J]. Operations research, 1997, 45(6): 805-819.
Clickstream-based demand forecasting model andcorporation inventory optimization under E-commerce environment
Xu Shengjia Jiang Wei
Based on the relationship of two representative data sets in E-commerce: data of clicking times and buying times, the demand was predicted dependent on historical clicking and buying information, and the forecasting model was theoretically validated. Considering E-commerce corporation with the minimum inventory cost as the optimal objective, this paper optimized the single period newsvendor model of E-commerce corporation, validated the model, its applicable criteria and the minimum probability of inventory cost reduction, analyzed the characteristics of corporation applying to this model, and also provided the corresponding inventory strategy for E-commerce corporations. By using data from Tmall, this paper launched an empirical research to validate the new model and its propositions. The results show that not every E-commerce corporation can improve the inventory management by applying the click-buy demand forecasting model, and E-commerce corporations should reduce inventory cost considering their own characteristics.
E-commerce; demand forecasting; inventory model
F272.1
A
1005-9679(2016)02-0018-10
国家自然科学基金项目(71531010),基于物联网的产品状态智能监控与质量管理。
许圣佳,上海交通大学安泰经济与管理学院硕士研究生,研究方向:统计预测,库存管理;蒋炜,上海交通大学安泰经济与管理学院特聘教授,运营管理系主任,研究方向:大数据与商务智能分析,数据质量与风险管理,物流与供应链管理。
