基于带权有向图的非清晰复杂精馏序列的合成方法

罗祎青，张焱，张硕，王菲，袁希钢,3



基于带权有向图的非清晰复杂精馏序列的合成方法

罗祎青1,2，张焱1，张硕1，王菲1，袁希钢1,2,3

（1天津大学化工学院，天津 300072；2天津大学化学工程研究所，天津 300072；3天津大学化学工程联合国家重点实验室，天津 300072）

在精馏系统中非清晰分离能够克服清晰分离所固有的返混效应，从而提高系统能效。基于数据结构理论，提出了非清晰精馏序列的合成与优化方法。对于组元混合物的分离，合成的精馏序列由1个精馏塔构成，且其中的非清晰分离任务含有所允许的任意多个中间分配组分。为了合成上述分离序列，利用带权有向图建立了一种新的精馏分离序列模型，并基于“vector”动态数组，提出了一个同时拥有数组和链表优点的带权有向图的储存结构。序列合成过程定义了一系列的相关操作，且选择广度优先的策略以提高合成效率。算例证明了该方法在精馏序列合成和优化的高效性。算例结果表明该算例的最优分离序列可以有效减少设备投资和能耗。

非清晰分离；分离序列；带权有向图；合成；精馏；系统工程

引 言

精馏是应用最普遍的化工分离单元，也是一个高能耗过程，因此对该过程进行优化设计具有十分重要的意义。对于多组元混合物分离，精馏序列中各组分的分离顺序对精馏系统的能耗及设备投资有着显著的影响。精馏序列的合成问题呈现大规模的组合特性，这种组合特性成为实现全局最优化的主要障碍之一[1]。最早的精馏序列合成的研究主要集中在简单-清晰塔分离序列的合成与优化，其研究方法包括经验规则法[2]、调优合成法[3]和数学规划法[4-6]等。但是，由于清晰分离固有的返混效应，致使其能效降低，而非清晰分离可以避免返混效应从而提高节能潜力。然而非清晰分离问题的潜在分离序列数目更大，该组合问题的规模也更大。对于该问题，最初的研究集中在含有一个中间分配组分的非清晰分离问题上[7-10]，发展出目前广受关注的Petlyuk塔分离结构，即分离三组元的隔板塔流程结构。近年关于非清晰分离序列的研究引起了广泛的关注，安维中[11]、Dong等[12]基于二叉树方法和模拟退火算法提出了精馏系统综合方法，但是该方法仅适用于含有一个中间组分时的非清晰分离问题。Agrawal等[13]研究了精馏序列合成有关搜索空间的问题，并指出多于-1塔的流程结构不仅设备投资增加，而且在节能方面也不占优势，因此好的搜索空间应该排除多于-1塔的流程结构。Shah等[14]用矩阵法产生所有的非清晰分离-1塔精馏流程，但是进料组分数较多时，由矩阵法得到的分离序列数量很多，从中筛选出较优序列工作量很大，这些缺点制约着矩阵法的使用与推广。Rong[15]以简单塔构成的非清晰序列作为起始点，通过调整精馏序列结构来合成少于-1塔的新型非清晰精馏序列，但是缺少系统合成和分离序列的评价。Torres-Ortega等[16]研究了改进的四组分非清晰精馏序列的设计与优化，基于过程强化原则减少精馏塔数量且序列中包含隔板塔，但仅限于四组分混合物进料的情况。

针对已有合成方法的缺陷，本文提出了基于数据结构理论的非清晰精馏序列合成方法，其中非清晰分离任务的中间分配组分数扩展到所允许范围的任意个。并且通过计算机程序对生成的序列进行高效的评价，从而可快速搜索出最优的非清晰分离序列。

1 问题描述

本文处理的问题可表述为已知（≥3）组元混合物进料条件和可用的公用工程条件，合成含多个中间分配组分的非清晰复杂塔精馏序列，寻找能满足分离要求（各组分的回收率≥0.98）且年度总费用（设备费+操作费）最小的-1塔流程结构。

为了方便和简化热力学性质及相平衡计算，做出以下几点假设：

（1）待分离的组元混合物不形成共沸物；

（2）序列中各个流股中各组分按照相对挥发度从大到小顺序排列；

（3）序列中的各流股均为饱和液体流股；

（4）各组分在每个精馏塔中的相对挥发度均视为常数。

这4点假设在精馏系统合成问题中被广泛采用。若采用严格热力学方法，本文提出的方法同样适用于具有共沸等特性的非理想物系分离序列合成。

2 组分的编码

使用自然数对系统进料中的组分进行编码。将组元混合物中的各组分按照相对挥发度从大到小排列，形式为C1, C2, C3, …, C-1, C，即C1是最易挥发组分，C2次之，C是最难挥发组分。例如5组分混合物C1C2C3C4C5的分离，由于精馏分离的特征决定任意流股中，组分在相对挥发度排列中一定是相邻的，所以，一个流股中可以用其中相对挥发度最高和最低的组分编码表示。例如，一流股含组分C2C3C4C5，则该流股可使用（2,5）表示。若流股中只含有一种组分C2，则用（2,2）表示。

而对于一个分离任务，可使用待分离的轻重关键组分编码表示。例如对于分离任务C2C3C4|C4C5，其轻关键组分为3，重关键组分为5，则该分离任务表示为（3,5）。

3 MINLP模型的建立及求解策略

非清晰精馏分离序列合成问题的MINLP模型如下：

min cost= min({S}LK,HK,/min)

其中，{S}∈，∈，LK∈[0.98, 1)，HK∈(0, 0.02]，/min∈[1.02, 1.5]。目标函数为年度总费用，包括分离序列的设备费和操作费；为所有可能的分离序列编码集合{S}；为各塔操作压力；LK和HK分别表示每个分离任务的轻重关键组分回收率；为实际回流比。

对组元进料进行非清晰分离时，其简单塔序列中精馏塔数目一定多于-1个，因此在构建-1塔分离序列的过程中，需大量进行两种操作，即：①创建简单塔；②将两个或数个塔合并成复杂塔，以构建-1塔流程。

该过程可概括为，从合成过程开始，一边随机生成合理的分力序列，一边向-1塔的形式调整。

本文基于Fenske-Underwood-Gilliland简捷法，对每个精馏塔进行设计计算，计算分离序列的年度总费用（TAC）并对每个分离序列进行评价。年度总费用是设备费与操作费之和，其中，设备费是指精馏塔及冷凝器和再沸器的设备费投资费用之和，相关的计算关联式基于Rathore等[17]和Douglas[18]的费用模型；操作费基于冷、热公用工程用量及价格进行求算。年度总费用最小的序列即为最优序列。

3.1 精馏塔模型的建立

精馏分离序列的拓扑结构可以简化地看作精馏塔和物流连接的集合。对于只有1股进料、2股出料的简单塔，可将塔看作顶点，进料是前驱，出料是后继，则这种结构与二叉树吻合。但是当序列中含有复杂塔的时候，二叉树不再能表示该结构，而这种结构可以用带权有向图很好地表示。

带权有向图是顶点和边的集合，据此可给出分离序列的定义。对于分离序列order，精馏分离单元unit和物料连接link，有这样一种关系，即order是unit和link的集合，表示为

order=(unit, link)

式中，order相当于图，unit相当于图中顶点，link相当于图中的边。

为方便建立精馏序列带权有向图模型，本文定义unit为1股进料及其对应的精馏塔的2个塔段（精馏段和提馏段），或者分离序列中最终的产品。如图1中的顶点①代表由a、b、c构成的简单塔，顶点②和③代表最终产品。

分离序列中塔间的物料连接link定义为连接unit的边，当边的权值为1时，表示该link为连接两个unit的管道；当权值为0时，表示连接两个unit的塔板，边用于表示复杂塔内塔段间的连接。例如，2个进料3个产品流股的复杂塔带权有向图模型如图2所示，权值为0的边表示连接两个塔段的塔板。

按照本文对图中顶点和边的定义，分离序列的带权有向图中，每个顶点（unit）最多有1个权值为0的前驱，1个权值为1的前驱，2个权值为1的后继，1个权值为0的后继。

根据该模型，简单塔合并为复杂塔的过程可通过删除1个待合并流股（2个组成相同的流股中的1个），然后创建1个权值为0的link（表示塔板）连接两个简单塔，如图3所示，左边为2个待合并的简单塔，其中④、⑥的组成相同，在合并过程中删除⑥，添加一个权值为0的边，获得合并之后的复杂塔模型。

3.2 数据结构的搭建

3.2.1 分离序列的数据结构 本文用带权有向图实现分离序列的结构表达，算法的实现需要将图的结构转换为编码表达，该编码必须能承载图的4种信息，包括顶点的值、边（指边连接了哪两个顶点）、边的方向和权值。

图的编码表达主要有3种实现方式，链表、数组和哈希表。链表增删元素很快，但查找慢；数组查找很快但增删元素慢，哈希表的这两种操作都很快，但需要一个特定的映射。对于分离序列合成问题，需要频繁地增删元素，极其频繁地查找，且很难找到一个合适的映射，所以，考虑搜索及求解效率，本文提出一种新的基于动态数组的储存方法来实现算法。该方法综合了链表和数组的特征，并继承其优点，即查找和增删元素都很快。这种方法主要使用了动态数组vector，能够存放任意类型的数据，并能对其进行增加和压缩[19]。

一个分离序列（order）由一个元素为顶点vertex的动态数组（以下简称顶点数组）表示，vertex中储存了前驱数组predecessor array、后继数组descender array、存在值existing value和顶点值vertex value共4种信息，其中前3种储存的是order的结构信息（即link的相关信息等），第4种储存的是每个vertex的值（即unit的相关信息）。

vertex中储存的结构信息如图4所示，其中前驱数组的组成元素是前驱predecessor，由前驱值predecessor value（即前驱vertex的序号）和前驱权值predecessor weight组成，后继数组与之相似。存在值为一布尔值，当取true时表示该vertex存在，取false时相反。

vertex中储存的顶点值信息如图5所示，顶点值vertex value中储存了共6种数据，其中层数layer指vertex到起始vertex的距离，越远则越大；流股类型stream type指unit的进料流股的类型，包括塔顶流股、塔底流股、侧线流股和起始流股；流股组分stream component指unit的进料流股的组成；分离方案separation solution指unit的分离方案；所属塔belonged tower和所属序号belonging number指unit所属的塔的种类和在其中的序号，所属塔为0代表简单塔，由于简单塔只含有一个unit，故序号为1，所属塔大于0表示其所属的复杂塔的序号，所属序号为该unit在其所属复杂塔中的位置，最顶端为1，向下递增。

考察这种数据结构，可以发现，本质上，这是一种数组，而在顶点的储存形式上，它更像链表。这种融合使其成功做到了两种（数组、链表）形式的扬长避短，即，遍历顶点迅速、增删元素迅速、能够实现快速双向查找且不依赖指针、拥有非常好的可扩展性。

关于可扩展性，其在结构信息和顶点值信息两个层面都有体现。在结构上，仅仅向vertex类中添加新的成员就可以做到扩展。比如在这个算法中不需要的彻底删除操作，只需在vertex中添加存在值这个成员即可。在值信息上，比如，可以给vertex value添加一个表示对应的进料的冷凝器选择的值，用不同的枚举值表示无冷凝器（热集成），分凝器或者全凝器。

该种数据结构的种种特征从根本上说是由面向对象的方法带来的。在本方法中，为了实现上述的结构，vertex作为一个对象被封装成类，其中储存的信息均为其成员变量，程序的一切操作都是基于vertex类的，上述种种优点皆来源于此，并以可扩展性最为突出。

对这种储存方式的相关操作定义如下。

（1）增加新顶点：在图（顶点数组）的末尾新建一个顶点。

（2）增加边：新建相应的前驱和后继并分别添加到两个顶点的前驱后继数组的末尾。

（3）删除边：将相应的前驱后继的权值赋为-1。

（4）删除顶点：将存在值赋为false，删除与之相关的边（删除方式见操作3）。注意，删除顶点的操作并没有删除该顶点本身，而是将其孤立。

（5）修改边：修改相应前驱后继的顶点序号。

按照以上定义，实际上合并复杂塔时被合并的两个流股都是留存在图中的，只是一个被修改成了侧线流股，另一个被孤立了。图3中复杂塔的结构实际上如图6所示，可见所有的操作仅涉及：在vector的末尾添加元素，修改元素中的值，vector的下标运算，而这些运算都是非常快的，这保证了采用这种方式的程序的运行速度。

3.2.2 记录栈的定义 为了使合成的序列为-1塔序列，需要记录每一个单元操作的详细信息，因此需要构建一个单元操作记录表来记录单元操作的全部信息。本文使用栈来实现这一功能。

栈（stack）在计算机科学中是限定仅在表尾进行插入或删除操作的线性表。栈是一种数据结构，它按照后进先出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据[19]。

建立一个储存元素为record的栈，record中储存的信息如图7所示，共3种数据。分离序列order；单元序号unit number，指创建简单塔时待分离unit的序号；全部分离方案all useful separation指所有可选的分离方案及其使用情况，任何分离方案都不能被重复使用，否则将大大降低效率。

3.3 确定-1塔的流程

3.3.1 程序算法 前面曾提到了分离序列流程合成过程中的两种操作，即：①创建简单塔；②将两个或数个塔合并成复杂塔，以构建-1塔流程。这两个操作被重复执行，直到所有组分都被合理分离开。算法的执行流程图如图8所示。

-1塔指的是经过精馏塔合并后，不存在同一个产品流股从不同的位置采出的分离序列[13]。对于组元混合物的非清晰分离，在不限制中间分配组分个数时，其创建的所有可能的分离序列中，-1塔序列只占相当小的一部分，而且无法定向创建一个-1塔序列。幸运的是，在创建简单塔的过程中，可以随时判断随机给出的分离序列是否会导致分离序列无法合成-1塔序列。如果不能的话，就需要将分离过程回滚到上一步，然后重新随机一个新的方案。

回滚操作定义为：用记录栈顶部的record中的分离序列（order）替代当前的分离序列，对record中储存的单元序号（unit number）对应的顶点进行重新随机分离，且分离方案不与已经使用过的重复。当分离方案耗尽时，推出顶部的record。

如果把分离序列的合成比作种树，那么分离的过程相当于接枝，回滚的行为相当于剪枝。由于−1塔的数量只占分离序列总组合数极少的比重，所以分离方案有很大的可能不满足−1塔的要求，这导致剪枝的次数非常多。从这个角度把一次完整的分离序列合成过程分为两个部分，正确的随机生长和错误的随机生长及剪枝，其中前者对应图8中的循环①，后者对应循环②。

3.3.2 分离策略 如3.3.1节所述，操作（1）是核心操作，包含2个关键选择，即选择合适的待分离流股和选择合适的分离方案；操作（2）则是被合并条件限制的，不需要进行过多判断的操作。因此，将主要分析操作（1）。

一条合适的流股必须符合两个条件，即它还没有被分离过，且不是纯组分流股。这两个条件都是显然的，但是在分离过程中，满足这两个条件的流股通常都有不止一条，所以流股选择是一个相当重要的问题，事实上，流股的选择策略在很大程度上影响着整个算法的效率。

对于符合上述显然条件的流股，有两种选择策略：广度优先和深度优先。参考层数（layer）的定义，这里，广度优先指的就是优先选择层数低的流股，深度优先指的是优先选择层数高的流股。考察两种做法的结果，按照3.3.1节中把分离序列比作种树，采用广度优先的策略得到的未完成的树的树枝数量多，且每根树枝的长度相似，采用深度优先的策略的树枝数量少，其中一些的长度要比其他的长得多，也比前者的长得多。

在此基础上，观察两种策略生成的树的形状，会发现，如果剪枝的位置随机，那么深度优先生成的树在除了生成过程的开头结尾之外，都有着更高的概率剪掉更长的一段枝。所以，选择广度优先能更好地减少错误的随机生长和剪枝的次数，这也可以理解为广度优先使剪枝的部位更有可能出现在树枝的末端。随着组分数的增加，完成一次运算的时间将逐渐到达秒级，此时，深度优先造成的时间延长非常显著，且带来的后果是难以承受的。

4 算 例

本算例取自安维中[11]的5组分轻烃分离问题。相关的进料条件和公用工程条件见表1、表2，进料流率（feed flow）为907.2 kmol·h-1。按前述方法得到的最优分离序列如图9所示。该序列对应的最优连续变量见表3。

表1 待分离混合物进料流率和摩尔分数

表2 公用工程条件

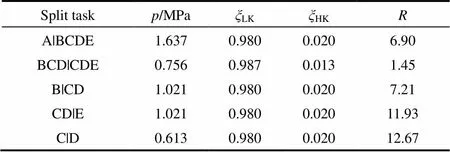
表3 算例最优结果

Note: total annual cost = 3.84066×105USD·a-1; operating cost = 2.94934×105USD·a-1; equipment cost = 0.89132×105USD·a-1

安维中[11]的最优分离序列如图10所示，计算结果对比见表4。表中，TAC代表年度总费用，OC代表操作费，EC代表设备费。可见用本方法能够高效合成含任意中间组分数非清晰分离序列。优化得到的序列的年度总费用相比安的简单-清晰分离序列有明显降低，约为19.2%。其中，操作费降低了约22.5%，为费用降低的主要原因，这是由于简单-清晰分离序列中，存在固有的返混效应，而非清晰分离任务可以克服这个缺点，从而提高热力学效率，降低年度总费用；设备费有少量的降低，约为6.3%，这是因为带有侧线采出的塔（即复杂塔）比对应的简单塔序列的塔板数的总和要少，因而它的投资费用更小[20]。

表4 与文献[11]算例年度总费用对比

5 结 论

提出了一种可以合成含任意中间组分数非清晰分离序列的方法，该方法基于新的使用带权有向图的精馏分离序列模型和新的带权有向图的储存方式，使用广度优先的搜索策略以提高算法的效率。

使用本文提出的方法对算例问题进行了分离序列的合成，得到了包含非清晰分离的最优精馏分离序列，非清晰分离序列在节能方面比清晰分离序列更有优势。本文的方法对非清晰复杂精馏序列合成问题是高效的。

[1] 袁希钢. 化工过程系统的组合特性及其最优化策略[J]. 化工学报, 1998, 49(S1): 2-9. YUAN X G. Combinatoral feature and optimization strategy for chemical process system [J]. Journal of Chemical Industry and Engineering (China), 1998, 49(S1): 2-9.

[2] THOMPSON R W, KING C J. Systematic synthesis of separation schemes [J]. AIChE Journal, 1972, 18(5): 941-948.

[3] NATH R, MOTARD R L. Evolutionary synthesis of separation processes [J]. AIChE Journal, 1981, 27(4): 578-587.

[4] ANDRECOVICH M J, WESTERBERG A. An MILP formulation for heat-integrated distillation sequence synthesis [J]. AIChE Journal, 1985, 31: 1461-1474.

[5] HENDRY J, HUGHES R. Generating separation process flowsheets [J]. Chemical Engineering Progress, 1972, 68: 71-76.

[6] NOVAK Z, KRAVANJA Z, GROSSMANN I E. Simultaneous synthesis of distillation sequences in overall process schemes using an improved MINLP approach [J]. Computers & Chemical Engineering, 1996, 20(12): 1425-1440.

[7] NATH R. Studies in the synthesis of separation processes [D]. Texas: University of Houston, 1977.

[8] MURAKI M, HAYAKAWA T. Synthesis of a multicomponent multiproduct separation process with nonsharp separators [J]. Chemical Engineering Science, 1988, 43: 259-268.

[9] ASPRION N, KAIBEL G. Dividing wall columns: fundamentals and recent advances [J]. Chemical Engineering and Processing: Process Intensification, 2010, 49: 139-146.

[10] DONAHUE M M, , ROACH B J, DOWNS J J,. Dividing wall column control: common practices and key findings [J]. Chemical Engineering and Processing: Process Intensification, 2016, 107: 106-115.

[11] 安维中. 基于随机优化的复杂精馏系统综合研究[D]. 天津: 天津大学, 2003. AN W Z. Synthesis of complex distillation systems based on stochastic optimization [D]. Tianjin: Tianjin University, 2003.

[12] LUO Y Q, YUAN X G, DONG F L. Synthesis and heat integration of thermally coupled complex distillation system [J]. International Journal of Energy Research, 2010, 34(7): 626-634.

[13] GIRIDHAR A, AGRAWAL R. Synthesis of distillation configurations (Ⅰ): Characteristics of a goodsearchspace [J]. Computers & Chemical Engineering, 2010, 34(1): 73-83.

[14] SHAH V H, AGRAWAL R. A matrix method for multicomponent distillation sequences [J]. AIChE Journal, 2010, 56(7): 1759-1775.

[15] RONG B G. A systematic procedure for synthesis of intensified nonsharp distillation systemswith fewer columns [J]. Chemical Engineering Research and Design, 2014, 92(10): 1955-1968.

[16] TORRES-ORTEGA C E, ERRICO M, RONG B G. Design and optimization of modified non-sharpcolumn configurations for quaternary distillations [J]. Computers & Chemical Engineering, 2015, 74: 15-27.

[17] RATHORE R N S, VAN WORMER K A, POWERS G J. Synthesis strategies for multicomponent separation systems with energy integration [J]. AIChE Journal, 1974, 20(3): 491-502.

[18] DOUGLAS J M. Conceptual Design of Chemical Processes [M]. New York: McGraw-Hill, 1988.

[19] LIPPMAN S B, LAJOIE J, MOO B E. C++ Primer [M]. Addison-Wesley, 2005.

[20] GLINOS K, MALONE M F. Optimality regions for complex column alternatives in distillation systems [J]. Chemical Engineering Research and Design, 1988, 66(3): 229-240.

Synthesis and optimization of nonsharp complex distillation sequences based on weighted directed digraphs method

LUO Yiqing1,2, ZHANG Yan1, ZHANG Shuo1, WANG Fei1, YUAN Xigang1,2,3

(1School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China;2Chemical Engineering Research Center, Tianjin University, Tianjin 300072, China;3State Key Laboratory of Chemical Engineering, Tianjin University, Tianjin 300072, China)

Nonsharp split can improve the thermodynamic efficiency of the distillation system due to its avoidance of the remixing effects which are inherent to sharp split. Based on the Data Structure Theory, a method is introduced to synthesize and optimize the nonsharp complex distillation sequences. For an-component mixture separation, the distillation sequences is comprised of−1 columns, the nonsharp splits of which contain an arbitrary number of middle components. In order to synthesize the separation sequences above, the weighted directed digraphs can be applied to establish a new model which is suitable for the distillation columns. Additionally, based on the dynamic array “vector”, a storage structure of the weighted directed graphs, which combines the advantages of arrays and chain tables, is proposed. A series of operations are defined in the synthesis procedure and the breadth-first strategy is chosen to improve the synthesis efficiency. An example problem is solved to illustrate the high efficiency of this method. The results show that the optimal sequence of the example problem can effectively reduce investment cost and energy consumption.

nonsharp split; separation sequence; weighted directed digraphs; synthesis; distillation; system engineering

date: 2016-08-31.

LUO Yiqing, luoyq@tju.edu.cn

10.11949/j.issn.0438-1157.20161215

TQ 021.8

A

0438—1157（2016）12—5098—07

国家自然科学基金项目（21676183）。

supported by the National Natural Science Foundation of China (21676183).

2016-08-31收到初稿，2016-09-02收到修改稿。

联系人及第一作者：罗祎青（1966—），女，副研究员。