第一眼位神经兴奋水平下人眼外肌收缩的本构模型

郭红梅,陈维毅,高志鹏

(太原理工大学 力学学院,山西省材料强度与结构冲击重点实验室,太原 030024)



第一眼位神经兴奋水平下人眼外肌收缩的本构模型

郭红梅,陈维毅,高志鹏

(太原理工大学 力学学院,山西省材料强度与结构冲击重点实验室,太原 030024)

为得到人眼外肌收缩的本构方程,修正眼球运动系统建模中眼外肌力学特性的描述,基于第一眼位的静态平衡,结合优化方法,并结合相关文献中斜视手术实验数据,用眼外肌的三线模型得到第一眼位神经兴奋水平下人眼外肌收缩的本构方程。用眼外肌的三线模型模拟左眼从鼻侧30°向颞侧20°的水平转动,在此过程中左眼各眼外肌都保持在第一眼位神经兴奋水平，模拟了两条水平直肌被剪断的情况下,左眼被动转动的情况；左眼从鼻侧向颞侧水平被动转动过程中,左眼外直肌的主动力、被动力和总力均呈非线性减小的趋势,内直肌的主动力、被动力和总力均呈非线性增大的趋势；当眼球处于鼻侧20°到颞侧5°的眼位范围内时,剪断两条水平直肌的模拟结果与前人文献中的实验结果吻合较好；当眼球处于鼻侧20°到颞侧5°的眼位范围内时,眼外肌收缩的本构方程有一定的合理性,可用于相应的眼球运动模型。本研究为临床眼科手术中手术量的确定提供个性化的理论依据。

三线模型;本构方程;眼球运动

第一眼位是指一个人的头部竖直固定的情况下其眼睛正视前方的位置[1]。无论是在人眼疾病的诊疗中还是在眼球运动建模中,第一眼位都是非常关键的眼位[2]。眼外肌力在眼球运动过程中起重要的作用,探究眼外肌力随眼球运动的变化规律对眼科临床有重要的意义。研究第一眼位神经兴奋水平下6条眼外肌的本构方程,可为眼球运动的有限元建模提供参考,进而为临床眼外肌手术的术前预测[3-4]提供理论依据。

前人做了很多实验来研究眼外肌力在眼球水平运动过程中的变化情况。通过侵害性的斜视手术以及正常志愿者非侵害性的眼外肌实验,前人已经确定了人眼水平固视运动中水平直肌的长度-张力关系[5-6]。在眼球的水平扫视运动中,水平直肌的等容张力也有报道[7-8]。前人的研究主要集中于水平直肌长度-张力特性的研究,其余4条眼外肌长度-张力特性数据的缺乏不利于眼球运动建模及眼外肌疾病中眼外肌手术量的确定。

对眼球运动建模的前提是要先弄清各眼外肌的长度-张力特性。前人建立的眼球运动模型很多都是用弹性的单线[9-10]来模拟眼外肌的,采取的都是简化的眼外肌力学特性。SCHUTTE et al建立了只含4条直肌的眼球运动有限元模型,其中将眼外肌的刚度定义为常数[11]。近年来,WEI et al[12]对眼球运动的有限元建模中,上下直肌和上下斜肌的长度-张力关系主要是在水平直肌长度-张力关系的基础上,用各眼外肌的横截面积作比例系数得出的[12]。在现有的眼球运动模型中,只有水平直肌的长度-张力关系是由实验得到的。除外直肌外,其余5条眼外肌的长度-张力关系(本构方程)是本文要研究的主要内容。在体实验实施难度很大的情况下,力学建模[13-15]是研究生物材料的力学特性最常用的方法。本文用眼外肌的三线模型(即用3条含长度-张力关系且横向相互约束的线来代替眼外肌条带)[16-17]研究第一眼位神经兴奋水平下人6条眼外肌的本构方程。

1 方法

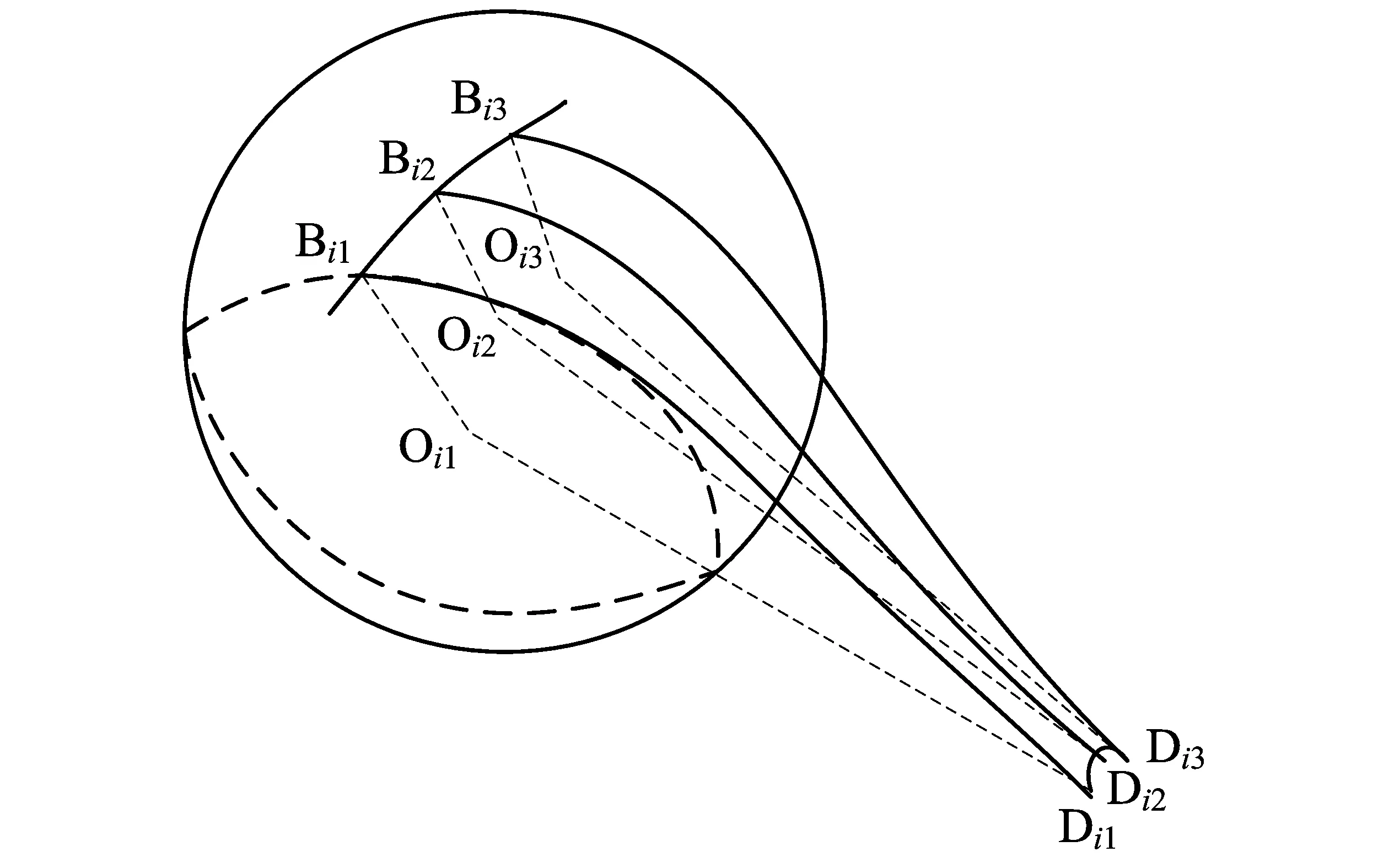
图1 第i条眼外肌的三线模型示意图Fig.1 Diagram of the three-string model of the i-th EOM

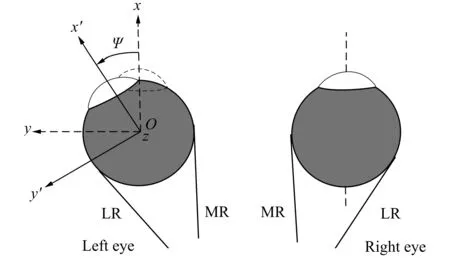
图2 建立有参考坐标系的双眼运动模型Fig.2 Double-eye movement model with the reference coordinate system

眼外肌的三线模型如图1所示[16-17],建立参考坐标系如图2(LR:外直肌;MR:内直肌)所示,左眼眼外肌的几何参数如表1所示[16,18]。通过对参考文献中的实验数据[5]进行拟合得到外直肌在第一眼位神经兴奋水平下的长度-总力关系和各眼外肌的长度-被动力关系。假定在第一眼位神经兴奋水平下,其余5条眼外肌的总应力-应变曲线可通过对外直肌的总应力-应变曲线沿总应力轴进行微小平移得到。基于眼球在第一眼位的静态平衡,通过优化即可得到各眼外肌的总应力本构方程。模拟COLLINS[5]的眼外肌实验,将模拟计算结果与实验结果进行对比,验证所得总应力本构方程的合理性。用经过验证的总应力本构方程减去被动应力本构方程即可得各眼外肌主动收缩的主动应力本构方程。

表1 左眼眼外肌关键点的坐标(上斜肌的起点指滑车)[16，18]

1.1 眼外肌的总应力本构方程

基于COLLINS[5]给出的外直肌的总力数据,结合表1所示的外直肌的参数可推导出外直肌在第一眼位神经兴奋水平下的本构方程:

σ1=12.82ε1+0.64exp(-6.53ε1)+0.51 .

(1)

式中:σ1表示外直肌沿长度方向的总应力;ε1表示外直肌沿长度方向的应变。

在外直肌的三线模型中,第j(j=1～3)条眼外肌线的本构方程如下:

σ1j=12.82ε1j+0.64exp(-6.53ε1j)+0.51 .

(2)

根据前面方法部分的假定即可得其余5条眼外肌的本构方程:

(3)

式中:σij0=12.82εij+0.64exp(-6.53εij)+0.51;dσij是待定的微小补充变量,i=1～6依次表示外直肌、内直肌、上直肌、下直肌、上斜肌和下斜肌,j=1～3分别为表1所示的各眼外肌线的编号。

对于本文中的三线模型,假定每条眼外肌线的横截面积均为相应眼外肌横截面积的1/3。因此,在第一眼位神经兴奋水平下,第i条眼外肌的总力。

(4)

基于前面的假设,式(3)中待定的补充变量dσij相对于σij0应该尽量小。因此,可用目标函数

(5)

来控制补充变量使其最小。

基于眼球在第一眼位的静平衡,六条眼外肌的力必须满足方程组(6)所表达的力矩平衡方程:

(6)

用Matlab中的quadprog函数求目标函数Φ在满足方程组(6)时的最小值,进而可得第一眼位神经兴奋水平下六条眼外肌的总应力。本构方程如下:

(7)

式中:i=1～6依次表示外直肌、内直肌、上直肌、下直肌、上斜肌和下斜肌;b1，b2，b3，b4，b5，b6依次为0.51，0.23，0.87，0.06，0.55，0.43。

1.2 眼外肌总应力本构方程的验证

由于人眼外肌的在体实验很难开展,只有COLLINS[5]的实验数据可与本文的计算结果进行对照。所以本文用图1给出的眼球运动模型结合1.1节所得眼外肌的总应力公式及总力公式,模拟COLLINS[5]将左眼内外直肌剪断后剩余其余四条眼外肌对眼球的阻力实验,计算将水平直肌剪断后其余4条眼外肌对眼球的阻力矩,再除以眼球的半径即可得相应的阻力值,最后将模拟结果与COLLINS[5]的实验结果进行对比。

1.3 眼外肌的被动应力本构方程

基于COLLINS文献[5,19]中外直肌在第一眼位神经兴奋水平下的被动力数据,可将三线模型中外直肌线的被动应力σp1j表示为(j=1～3分别为表1所示各眼外肌线的编号):

σp1j=-0.72ε1j+0.29exp(9.03ε1j)-0.18 .

(8)

眼外肌的被动力主要依赖于眼外肌长度的变化,忽略其他因素的影响,认为眼外肌的被动力只与材料本身有关,那么6条眼外肌中各眼外肌线的被动应力本构方程可依照式(8)描述为:

σpij=-0.72εij+0.29exp(9.03εij)-0.18 .

(9)

式中，i=1～6依次表示外直肌、内直肌、上直肌、下直肌、上斜肌和下斜肌。

6条眼外肌中各眼外肌线的被动力为:

(10)

各条眼外肌的被动力可表示为:

(11)

1.4 眼外肌的主动应力本构方程

由前面所得6条眼外肌线的总应力本构方程式(7)减去相应眼外肌线的被动应力本构方程式(9)即可得各眼外肌线的主动应力本构方程如下:

(12)

式中：i=1～6依次表示外直肌、内直肌、上直肌、下直肌、上斜肌和下斜肌；c1，c2，c3，c4，c5，c6依次为0.69，0.41，1.05，0.24，0.73，0.61。

各眼外肌线的主动力可由下式求得:

(13)

各眼外肌的主动力可由下式求得:

(14)

2 结果

2.1 眼外肌的总力及总应力本构方程的验证结果

图3 在第一眼位神经兴奋水平下左眼各眼外肌的总力Fig.3 Total forces of the EOMs of left eye in the primary innervations

从图3(LR:外直肌;MR:内直肌;SR:上直肌;IR:下直肌;SO:上斜肌;IO:下斜肌;N:鼻侧;T:颞侧)可以看出,当眼球在鼻侧30°到颞侧20°的转动过程中,内直肌和外直肌总力的变化幅度最大。左眼从鼻侧30°向颞侧20°水平转动的过程中,外直肌的总力从440.96 mN非线性地减小为75.93 mN。与此相反,内直肌的总力从5.65 mN非线性地增大到308.52 mN。上下直肌的总力在整个眼球运动过程中变化不明显,各自维持在某一特定值附近。在图3所示的眼球运动过程中,上直肌的总力在165 mN附近略微波动;下直肌的总力在100 mN附近有微小起伏;上斜肌的总力在180～240 mN之间呈缓慢增大的趋势;与上斜肌的总力相比,下斜肌的总力上升趋势较为明显,从108.60 mN非线性地缓慢上升至216.21 mN。对比除水平直肌外其余4条眼外肌对眼球阻力的计算结果与COLLINS[5]的实验结果,可以看出当眼球处于鼻侧20°到颞侧5°的眼位范围内时,模拟结果与COLLINS[5]的实验结果吻合较好(图4)。

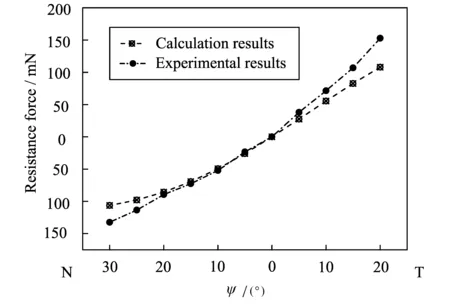
图4 除水平直肌外其余4条眼外肌对眼球的阻力Fig.4 Resistance forces from the other four EOMs,except for the horizontal recti

2.2 眼外肌的被动力

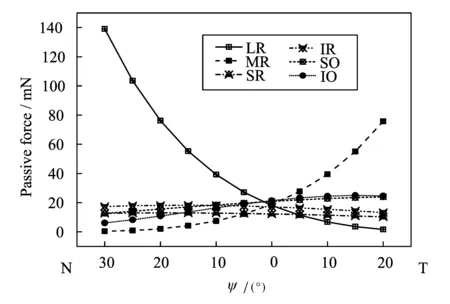
图5 左眼各眼外肌的被动力Fig.5 Passive forces of the EOMs of left eye

从图5中可以看出,内外直肌的被动力在眼球水平运动过程中变化最为明显。左眼从鼻侧30°到颞侧20°水平运动的过程中,外直肌的被动力从139 mN非线性地快速减小至1.63 mN;与此相反,内直肌的被动力则从0.47 mN非线性地上升至75.75 mN;其余四条眼外肌的被动力变化都较小,上直肌的被动力几乎一直维持在11 mN;下直肌的被动力基本维持在16 mN;上下斜肌的被动力则在6 mN到25 mN的小范围内变化。

2.3 眼外肌的主动力

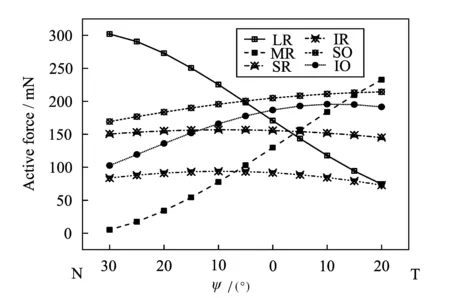
图6 在第一眼位神经兴奋水平下左眼各眼外肌的主动力Fig.6 Active forces of the EOMs of lefteye in the primary innervations

从图6可以看出,左眼从鼻侧30°向颞侧20°水平运动的过程中,内外直肌的主动力变化最为明显,外直肌的主动力从301.96 mN非线性地减小为74.30 mN;内直肌主动力的变化趋势则正好相反,从5.18 mN非线性地增大到232.77 mN;其余4条眼外肌中,主动力变化最明显的是下斜肌,下斜肌的主动力从169.32 mN逐渐增大到214.25 mN;上斜肌的主动力在170 mN到215 mN范围内小幅增长;上下直肌的主动力分别维持在150 mN和80 mN附近。

3 讨论

6条眼外肌控制着眼球的运动,斜视等眼外肌疾病的治疗与眼外肌的本构方程有着直接的关系。而在斜视的治疗过程中,第一眼位各眼外肌的力学特性尤为关键。在水平的内斜视和外斜视手术中,可用内外直肌的长度-张力关系[5]来估计眼外肌的手术量,但垂直斜视[19]及旋转斜视[20]的手术治疗还需要分别弄清上下直肌和上下斜肌的长度-张力关系。而前人的研究并没有明确地给出这4条眼外肌的长度-张力特性。本文旨在研究第一眼位神经兴奋水平下6条眼外肌收缩的本构方程,为眼外肌疾病中眼外肌手术量的确定提供理论依据。

本文假定在第一眼位神经兴奋水平下,其余5条眼外肌的总应力-应变曲线可通过对外直肌的总应力-应变曲线沿总应力轴进行微小平移得到。以外直肌在第一眼位神经兴奋水平下的长度-张力数据[5]为基础,通过优化方程和力矩平衡方程,得到第一眼位神经兴奋水平下,6条眼外肌的总应力本构方程。并应用三线眼外肌眼球运动模型[16]及本文所得总应力本构方程及总力公式模拟当内外直肌剪断的情况下,其余4条眼外肌对眼球的阻力实验[5],并将模拟计算出的结果与实验结果进行对比(图4)。再结合眼外肌的被动应力本构方程求出其主动收缩的本构方程。可以看出(图4),虽然当眼球处于鼻侧20°到颞侧5°的眼位范围内时,两种阻力结果非常接近,但随眼球转动角度的增大,两者之间的误差有增大的趋势。当眼球转到鼻侧30°时,计算结果为106.34 mN,实验结果为132.34 mN,二者误差是26 mN;当眼球转到颞侧20°时,计算结果为107.91 mN,实验值为152.84 mN,二者的误差为44.93 mN。误差可能是由于本文所采用的眼眶几何参数与实验[5]所用志愿者的眼眶几何参数之间的差异造成的。

本文的计算结果(图3,图5和图6)表明,在第一眼位神经兴奋水平下,内外直肌力(无论是被动力、主动力还是总力)的变化幅度最大。这是因为在眼球的水平运动过程中,内外直肌的长度变化远大于其余4条眼外肌的长度变化。当眼球从鼻侧30°向颞侧20°转动的过程中,外直肌的各种力呈非线性减小的趋势,内直肌的各种力呈非线性增大的趋势。分析其原因,眼外肌被动力的变化主要依赖于相应眼外肌长度的变化。那么,在眼球从鼻侧向颞侧水平地转动过程中,外直肌的长度逐渐减小,内直肌的长度逐渐增大,按照肌肉的被动受力规律可以直观地判断出,外直肌的被动力会随外直肌长度的减小而减小,内直肌的被动力会随内直肌长度的增大而增大。而眼外肌主动力的变化规律主要依赖于微观上肌小节的收缩。

本文在第一眼位神经兴奋水平下,从外直肌的相关实验数据得到其余5条眼外肌的本构方程,并对其合理性进行了验证。结果表明当眼球处于鼻侧20°到颞侧5°的眼位范围内时,本文所得眼外肌收缩的本构方程有一定的合理性。所得眼外肌的本构方程可为眼球运动建模中各眼外肌力学特性的选择提供参考,进而通过建立相应的眼球运动模型为临床上眼外肌疾病患者眼外肌手术量的术前预测提供个性化的理论依据。

[1] BUCHBERGER M.Biomechanical modelling of the human eye[D].Doctoral Dissertation of Johannes Kepler Universität,2004.

[2] GAO Z P,GUO H M,CHEN W Y.Initial tension of the human extraocular muscles in the primary eye position[J].J Theor Biol,2014,353(21):78-83.

[3] GRAEF M,LORENZ B.Strabismus[J].Monatsschrift Kinderheilkunde,2015,163(3):230-240.

[4] JIAO Y,ZHU Y,ZHOU Z,et al.Strabismus surgery distribution during 10-year period in a tertiary hospital[J].Chinese Medical Journal,2014,127(16):2911-2914.

[5] COLLINS C C.Orbital mechanics[M].B-Y-R P,COLLINS CC,HYDE J E.(Eds.), The Control of Eye Movements,New York:Academic Press,1971:283-325.

[6] COLLINS C C,CARLSON M R,SCOTT A B,et al.Extraocular muscle forces in normal human subjects[J].Invest Ophthalmol Vis Sci,1981,5(20):652-664.

[7] LENNERSTRAND G,SCHIAVI C,TIAN S,et al.Isometric forces measured in human horizontal eye muscles attached to or detached from the globe[J].Graefe’s Arch Clin Exp Ophthalmol,2006,244:539-544.

[8] LENNERSTRAND G,BOLZANI R,BENASSI M,et al.Isometric forces development in human horizontal eye muscles and pulleys during saccadic eye movements[J].Acta Ophthalmol,2009,87:837-842.

[9] QUAIA C,OPTICAN L M.Dynamic eye plant models and the control of eye movement[J].Strabismus,2003,11(1):17-31.

[10] QUAIA C,SHAN X,TIAN J,et al.Acute superior oblique palsy in the monkey:effects of viewing conditions on ocular alignment and modelling of the ocular motor plant[J].Progress in Brain Research,2008,171:47-52.

[11] SCHUTTE S,BEDEM S V D.A finite-element analysis model of orbital biomechanics[J].Vision Res,2006,46(11):1724-1731.

[12] WEI Q,SUEDA S,PAI D K.Physically-based modeling and simulation of extraocular muscles[J].Prog Biophys Mol Biol,2010,103:273-283.

[13] 高志鹏,陈维毅.滑车组织在眼球内旋运动时维持眼外肌力学优势的模拟研究[J].医用生物力学,2014,6(29):498-503.

[14] 樊瑜波.生物力学建模及应用的几个研究[J].医用生物力学,2013,28:12-14.

[15] LIU M C,WU X L,LIN C X,et al.Construction of a 3D finite element model of temporomandibular joints including the musculoskeletal system[J].Journal Med Biomech,2015,2(30):118-124.

[16] 陈维毅.眼球的运动模型及其临床应用的研究[D].太原工业大学博士学位论文,1996:9.

[17] 陈维毅,杨桂通,吴文周.人体眼球的运动模型及相应的动力学方程组[J].中国生物医学工程学报,2000,3(19):266-271.

[18] PASCOLO P,CARNIEL R.From time series analysis to a biomechanical multibody model of the human eye[J].Chaos Solitons Fractals,2009,40:966-974.

[19] CAPUTO R,TINELLI F,BANCALE A,et al.Motor coordination in children with congenital strabismus:effects of late surgery[J].Eur J Paediatr Neuro,2007,11:285-291.

[20] FELIUS J,LOCKE K G,HUSSEIN M A,et al.Photographic assessment of changes in torsional strabismus[J].Journal of AAPOS,2009,13:593-595.

(编辑：朱 倩)

Contractile Constitutive Model of Human Extraocular Muscle in Primary Innervation

GUO Hongmei,CHEN Weiyi,GAO Zhipeng

(College of Mechanics, Shanxi Key Laboratory of Material Strength & Structural Impact,TaiyuanUniversityofTechnology,Taiyuan030024,China)

The purpose was obtaining the contractile constitutive equations of extraocular muscles (EOMs) in order to amend the description of the mechanical properties of EOMs in the modeling of oculomotor system and provide a quantitative prediction to clinical EOM surgery theoretically. Three-string model of EOM and an optimal method were used to obtain the contractile constitutive equations of EOMs in primary position on the basis of the static equilibrium and the previous data from strabismus surgery. The horizontal rotation of left eye was simulated from nasal 30° to temporal 20° by using the three-string model of EOMs, while the EOMs of left eye was kept in primary innervations. And the passively horizontal rotation of left eye, with two horizontal recti detached, was also simulated. The active force, passive force, and the total force of lateral rectus decreased nonlinearly during the simulated eye movement, whereas those of medial rectus increased nonlinearly. When eye rotated from nasal 20° to temporal 5°, the simulation results with two recti detached agreed well with the previous experimental data. When eye rotated from nasal 20° to temporal 5°, the obtained contractile constitutive equations of EOMs were reasonable to a certain degree. And the constitutive equations can be used to establish the corresponding eye movement model, which will provide a personalized theoretical direction to determination of the surgical amount of EOMs in clinical surgery.

three-string model;constitutive equation;eye movement

1007-9432(2016)05-0658-06

2016-03-03

国家自然科学基金资助项目：眼球功能相关疾患治疗机理的力学生物学研究(11032008)，用胶原交联术治疗高度近视眼及圆锥角膜的力学生物学机理研究(31271005)

郭红梅(1987-)，女，山西汾西人，博士，主要从事生物力学研究，(E-mail)guohongmeiguo@sina.com

陈维毅，教授，博士生导师，主要从事生物力学研究，(E-mail) chenweiyi211@163.com

R318.01

A

10.16355/j.cnki.issn1007-9432tyut.2016.05.018