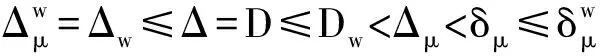基于弱测量的Werner态的量子关联

郝小宁

(太原理工大学 数学学院，太原 030024)



基于弱测量的Werner态的量子关联

郝小宁

(太原理工大学 数学学院，太原 030024)

给出强单边非局域量子失协及弱单边非局域信息亏损的概念,证明强单边非局域量子失协总是大于等于单边非局域量子失协,并研究Werner态的量子关联间序的关系。

Werner态;量子关联;弱测量

量子纠缠在量子信息和量子计算中起着非常重要的作用。近几十年来,量子纠缠的研究已受到物理学、计算机科学、信息学、数学等领域科学家们的广泛关注[1]。在2001年,OLLIVIER et al[2],HENDERSON et al[3]指出量子纠缠并不能包含所有的非经典关联,即使在可分态中包含的量子关联也不完全是经典的,随后他们引入量子失协的概念来描述这类非经典关联。量子失协是互信息与最大经典互信息之间的差,因而它度量总的关联与经典关联之间的差。这一概念的提出引起相关学者的广泛关注并进行深入研究。特别的对于two-qubit 态的量子失协,可以得到解析的表达式[4]。在不同噪声环境下的量子失协的动力学研究也揭示许多有趣的结论[5-6]。近年来,弱测量[7]也被应用到量子关联的研究中。基于弱测量,SINGH 和PATI 提出超量子失协[8],并证明超量子失协总是大于等于量子失协,此说明弱测量有时能揭示更多的量子信息。另一方面,基于弱测量,WANG et al[9]还提出弱单边亏损概念,并证明弱单边亏损小于单边亏损,从而说明弱测量并不总是揭示更多的量子信息。笔者基于弱测量提出强单边非局域量子失协及弱单边非局域信息亏损的概念,证明强单边非局域量子失协总是大于等于单边非局域量子失协,并对2×2的Werner态给出量子关联间序的关系。

下面介绍本文的一些基本概念及符号表示。∏0和∏1是Hiltbert空间上的2个正交投影并且满足∏0+∏1=I . x是测量强度参数,x∈[0,+∞) .

则{P(x),P(-x)}是一组测量,这种测量称为弱测量。

本文把完备的测量基底限制在von Neumann测量上。Hilbert空间H=HA⊗HB,dimHA=n,dimHB=2,S(H)是H上的量子态集合,ρ∈S(H),用S(ρ)代表量子态ρ的熵。

1 强单边非局域量子失协与弱单边非局域信息亏损

先回顾一些相关定义。单边非局域量子失协δμ(ρ)的定义[10]。

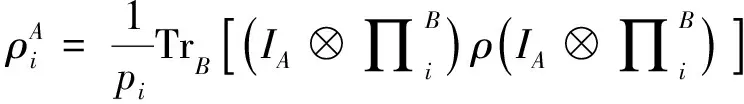
单边非局域信息亏损Δμ(ρ)的定义[11]。

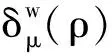
式中：

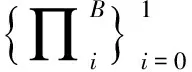
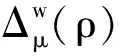
式中：

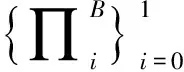
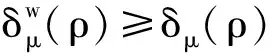
证明 因为

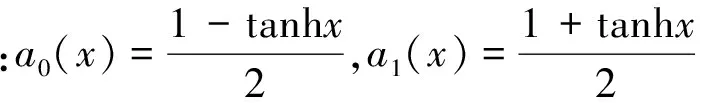
现在定义弱测量算子,

根据定义1,可以得到

因此,

即对B系统进行弱测量得到的强单边非局域量子失协总是大于等于单边非局域量子失协。

2 Werner态的量子关联

量子信息学的一个很重要的资源就是量子纠缠,最具有代表性的就是EPR态。但是由于消相干的原因,纠缠态可能会发生退化。在这些退化的态中,有一种典型的特殊态Werner态。因此,对Werner态的研究很重要。Werner态是d×d的两体量子态,其中d是Hilbert空间的维数。在酉算子U的作用下,都满足ρ=(U⊗U)ρ(U+⊗U+),可看出这种酉变换不改变Werner态的熵。此部分研究2×2的Werner态,即

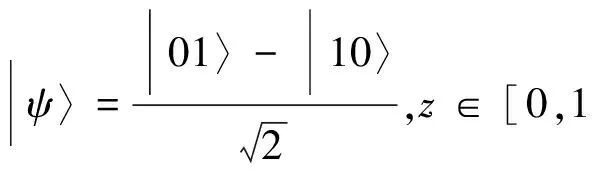
因此,

根据定义2,可得到Werner态的弱单边非局域信息亏损的解析表达式是

STRELTSOVEetal给出单边亏损Δ(ρ)的定义[12]。对两体态的单边亏损是

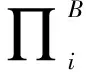
式中,

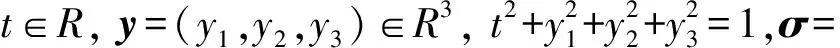
利用下面这组关系,

可以得到,

式中：c1=c2=c3=-z；z1:=2(-ty2+y1y3)；

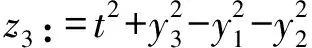
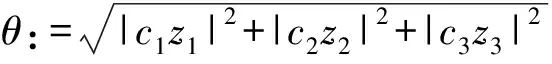
进而,得到Werner态单边非局域信息亏损的解析表达式:

Werner态的超量子失协的解析表达式[8]是

通过文献[5],可以得到Werner态的单边亏损Δ(ρ)的解析表达式是

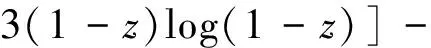
WANG et al给出弱单边亏损的解析表达式[9]是

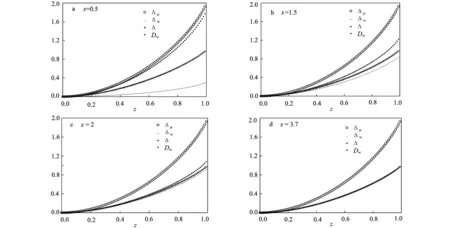
在图1中,本文就Werner态给出单边非局域信息亏损、弱单边亏损、单边亏损、超量子失协随z的曲线图。我们发现在图1(a),1(b),1(c)中,单边非局域信息亏损大于超量子失协,超量子失协大于单边亏损,单边亏损大于弱单边亏损(即Δw<Δ

图1 单边非局域信息亏损、弱单边亏损、单边亏损、超量子失协随z的变化图Fig.1 One-way unlocalizable in formation deficit,weak one-way deficit,one-way deficit,superquantum discord as functions of z

[1] 李波，范桁.量子关联及其应用[J].中国科学，2014，44(3):360-369.

[2]OLLIVIERH，ZUREKWH.Quantumdiscord:ameasureofthequantumnessofcorrelations[J].PhysicalReviewLetters，2001，88:017901.

[3]HENDERSONL，VEDRALV.Classical，quantumandtotalcorrelations[J].JournalofPhysicsAGeneralPhysics，2001，34(35):6899-6905.

[4]LUOS.Quantumdiscordfortwo-qubitsystems[J].PhysicalReviewA，2008，77(4):140.

[5]HANF.ThedynamicsofquantumcorrelationanditstransferindissipativeSystems[J].InternationalJournalofTheoreticalPhysics，2011，50:1785-1792.

[6]MIYJ.Classicalcorrelationandquantumdiscordinatwoqubitsystemunderdissipationenvironments[J].InternationalJournalofTheoreticalPhysics，2012，51:544-553.

[7]ORESHKOVO，BRUNTA.Weakmeasurementsareuniversal[J].PhysicalReviewLetters，2005，95(11):643.

[8]SINGHU，PATIAK.Superquantumdiscordwithweakmeasurements[J].AnnalsofPhysics，2014，343(4):141-152.

[9]WANGY，MAT，FANH，etal.Super-quantumcorrelationandgeometryforbell-diagonalstateswithweakmeasurements[J].QuantumInformationProcessing，2014，13(2):283-297.

[10]XIZ，FANH，LIY.One-wayunlocalizablequantumdiscord[J].PhysicalReviewA，2012，85(5):1222-1228.

[11] 朱学娜.量子纠缠度量和量子关联[D].广州:华南理工大学，2014.

[12]STRELTSOVA，KAMPERMANNH，BRUβD.Quantumcostforsendingentanglement[J].PhysicalReviewLetters，2012，108(25):59-62.

(编辑：朱 倩)

Quantum Correlation of Werner State Based on Weak Measurements

HAO Xiaoning

(College of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China)

In the paper, we give the definition of strong one-way unlocalizable quantum discord and weak one-way unlocalizable information deficit, and prove that strong one-way unlocalizable quantum discord is always greater than or equals to one-way unlocalizable quantum discord. Finally, we give the order relation for Werner state.

Werner state;quantum correlation;weak measurements

1007-9432(2016)05-0680-05

2015-10-15

国家自然科学基金资助项目：纠缠破坏信道和量子测量的代数结构和几何特征(11201329)，山西省国际合作项目:基于算子理论的量子关联性研究(2014081027-2);太原理工大学青年基金资助项目：量子连续变量系统的信道表示及新一代保密通信系统的数据协调技术研究开发(2014QN024)

郝小宁(1980-)，女，山西太原人，博士生，主要研究方向为算子及量子信息与量子计算，(E-mail)haoxiaoning@tyut.edu.cn

O413.1

A

10.16355/j.cnki.issn1007-9432tyut.2016.05.022