基于项目云的有序秩聚类在推荐系统中的应用

杜宗宴,景英川

(太原理工大学 数学学院,山西 晋中 030600)



基于项目云的有序秩聚类在推荐系统中的应用

杜宗宴,景英川

(太原理工大学 数学学院,山西 晋中 030600)

为进一步提高推荐系统的推荐精度,提出一种新的基于项目云的有序秩聚类协同过滤推荐算法,其中包括三大步:数据处理,有序聚类，生成推荐。该方法不仅借助定性分析思想利用项目云有效地填充了缺失数据,而且通过对项目分布的数字特征做排序、分割、聚类,在类内产生“邻居”,大大缩短了计算时间。通过在MovieLens数据集上的实验表明,在平均绝对误差和预测精确度上,该算法确实优于传统推荐算法。

协同过滤;云模型;有序秩聚类;评分可靠度;推荐系统

近年来,随着科学技术的不断发展,网络数据与日俱增。特别是像Facebook, Amazon, Alibaba[1]等这样的商务网站,其在线用户对产品的评分数据更是呈指数趋势迅猛增加。因此,建立一个有效的个性化推荐系统对于商家推广产品及用户挖掘新品都是十分重要的。

目前,协同过滤是推荐系统中应用最广泛、最成功的一种算法,该算法最初由TYPESTRY提出,它认为目标用户会与其相关用户表现出相同偏好[2]。之后,GROUPLENS提出一个专门用于推送新闻、电影等的开放自主协同过滤推荐系统,认为用户会对相似的项目产生相同兴趣[3]。基于此,为进一步提高推荐精度,国内外学者将协同过滤算法系统地分为两大类:基于内存和基于模型。基于内存的协同过滤算法又包括User-based、Item-based协同过滤,其实质都是通过对用户-项目信息进行统计分析,最终为目标用户(或目标项目)挖掘一些具有历史相似性行为的用户(或项目)[4]。而基于模型的协同过滤则是依托统计或机器学习方法,利用历史数据构成用户偏好模型进行预测与推荐的方法,其中最典型的有基于关联规则、贝叶斯网络等的推荐算法[5]。

协同过滤技术虽已广泛应用于许多电子商务过程中,但与之相伴的用户-项目评分矩阵的极端稀疏性、冷启动[6]等问题也日益凸显。HUANG et al提出了基于关联规则的协同过滤算法[7];WENG et al深入探索用户分类与评分偏好的内部关系[8];BACKSTROM et al采用社交网络模型进行预测和推荐[9];CAI et al提出了基于典型度的协同过滤推荐算法[10]。这些方法虽然都不同程度的提高了推荐精度,但并未改善数据稀疏性。同时,还有许多学者试图从模糊学的角度来解除冷启动对预测结果的影响。张光卫等引入了云模型相似性度量方法(LICM)[11];余志虎等提出了云模型数据填充算法来弥补数据缺失性[12];孙金刚等提出了基于项目属性和云填充的协同推荐算法[13]。这些算法填充数据时均是采用均值填充、众数填充或随机填充等,并未充分考虑项目本身的性质特征,因此预测精度也不尽如人意。

基于此,本文借鉴模糊聚类的思想,结合云模型[14]与有序秩聚类[15]的优点,提出了一种基于项目云的有序秩聚类协同过滤推荐算法(Ordered Rank Cluster in Collaborative Filtering Recommendation Based on Item Cloud, ICORC)。较之于传统算法,该方法从以下三点进行了改进。首先,通过拟合项目的分布情况来填充原始数据矩阵,不仅弥补了原始数据矩阵的极端稀疏性,而且缓解了冷启动问题引起的推荐不精确;其次,该算法依据项目分布的统计信息和评分概率分布情况恢复原始项目矩阵,较完整的还原了原始项目的数据特征;最后,该算法仅在相邻用户间进行有序秩聚类为目标项目产生最近邻用户,大大缩短了计算时间。据了解，目前尚未有研究将有序秩聚类与传统推荐算法结合。

1 基于项目云的有序秩聚类协同过滤算法

协同过滤推荐算法的假设前提是用户对于同类型的项目通常会表现出相似的兴趣。由于用户评分行为具有极大的不确定性、主观性和模糊性,因此,本文从模糊角度出发,提出了一种基于项目云的有序秩聚类协同过滤推荐算法。该方法的推荐机制如下。

1) 通过项目云数字特征C(E,En,H)来拟合每一个项目的分布情况；

2) 根据所拟合的项目分布来生成缺失数据以恢复原始稀疏评分阵；

3) 将所有的项目按其数字特征排序,并计算相邻两者间的相似度；

4) 根据相似度进行有序秩聚类；

5) 对目标用户在类内选择“邻居”并作出推荐和预测。

1.1 数据预处理

在协同过滤推荐系统中,用户-项目评分矩阵可以用一个m×n阶矩阵Am×n来表示,如表1所示。我们将m个用户的集合记为U={U1,U2,…,Um},n个项目的集合记为I={I1,I2,…,In},用户的评分集合记为X={xij, i=1,2,…,m; j=1,2,…,n}。其中,xij表示用户Ui对项目Ij的评分值(“NA”表示缺失值)。通常,用户对项目的评分都用1到5之间的整数值来表示,即{1,2,3,4,5},且不同分值表示用户对项目的不同偏好程度,本文选取的实证数据集采用的正是此种评分机制。

表1 用户-项目评分矩阵Am×n

1.1.1 数据缺失及分布假设

一般而言,用户的个人偏好、周遭环境、事务本身等都会为其行为决策带来极大的不确定性和随机性。基于此,本文对数据的缺失机制作出假设,认为用户对项目是否进行评分是完全随机的。换言之,用户对某个项目是否评分是一个随机事件,且评分与否并不代表用户对该项目的喜恶。但是,用户的评分高低却可以直观反映其对项目的偏好程度,即分值越大,表明用户对该项目越感兴趣;反之,分值越小,兴趣越低。因此,本文假设数据的缺失机制为随机缺失。

另外,由于在推荐系统的研究中多数采用的是用户对一些项目的评分数据,然而在用户未对项目作出评分之前,每个用户给出1,2,3,4,5分的可能性是相同的。因此,这些评分值可看作是相互独立的随机变量,且事件1, 2, 3, 4, 5的发生可认为是等概率事件。故从理论角度出发,根据伯努利大数定律及中心极限定理,我们假设每一个项目的用户评分均可近似看成是服从正态分布且相互独立的随机变量。

1.1.2 数据填充

研究资料表明,稀疏性是用户-项目评分矩阵最明显的问题,传统的协同过滤推荐算法,虽然采用了多种方法去克服这种稀疏性,但结果都不理想。原因在于,用户打分存在主观性、局限性。特别是当用户参与打分项目较少时,其评分的可参考价值就会很小。基于此,本文提出了用户评分可靠度如下,认为参与评分项目越多的用户,其评分结果越具代表性。

定义1(评分可靠度) 设用户Ui对所有项目的评分向量为Xi=(xi1,xi2,…,xin),(xij表示用户Ui对项目Ij的评分值,n为项目总数),记Xi=(xi1,xi2,…,xin)中非零项的个数为fi(i=1,2,…,m)(m为用户总数),则用户Ui的评分可靠度可用ωi来表示,如式(1),且满足:

(1)

另一方面,现实生活中用户对项目的评分行为本身就具有强烈的主观性、模糊性以及不精确性。因此,我们引入云模型概念以及其基本数字特征:期望、熵、超熵[14],来描述项目的分布情况,称之为项目云。其中,期望E为用户对某项目的平均评分;熵En表示用户对该项目评分的方差;超熵H是熵的熵。本文的研究中将依据项目云的数字特征,对比使用普通云发生器与加权云发生器来填充缺失值。其具体操作步骤如下:

1) 利用式(2),式(3)逆向云发生器(Backward Cloud Generator,BCG)来拟合每一个项目的分布情况,并通过云模型数字特征C(E,En,H)来表示。其中，ωi为用户Ui的评分可靠度；Ej,En，j,Hj分别表示项目Ij的期望、熵、超熵；nj表示项目Ij的评分中非零值的个数；Sj表示项目Ij的标准差；Cj(Ej,En，j,Hj)为项目Ij的分布特征向量。则普通逆向云发生器计算见式(2),加权逆向云发生器计算见式(3):

(2)

(3)

2) 利用正向云发生器(ForwardCloudGenerator,FCG)生成每个项目对应数量的随机数,并计算每个随机数隶属于该模型的隶属度

3) 根据已评分值中各项目得分情况,对生成的随机数进行划分和数值转换,填充缺失值。设pkj为项目Ij评分为k(k=1,…,5)的理论概率,若p(k-1)j<μij≤pkj,则xij=k.

在整个数据填充过程中,我们假设数据缺失机制为完全缺失;在获取项目分布时充分考虑到用户评分可靠度,因此对比采用普通云发生器和加权云发生器分别获得项目分布,生成缺失数据,并通过隶属度将生成的连续数值离散化,最终实现用户-项目评分矩阵的稠密化。

1.2 有序秩聚类

1.2.1 相似度计算

在之前的讨论中,我们已经知道可以用项目云C(E,En,H)来反映项目的性质特征。因此,处于相同位置、拥有相似形状的云,其数字特征可能更相近,也更可能属于同一类别。基于此,本文在计算项目相似度之前,首先将所有项目按一定的排序准则重新排列,保证相邻项目尽可能相似。值得注意的是,在项目云数字特征E、En、H中,E是最能代表用户对项目的平均偏好程度,E值越高表明项目越受欢迎,故排序时优先考虑E;其次排列En,因为En代表用户对项目评分的离散程度,En值越小表明该项目评分值越集中;而H相当于En的方差,反映的是用户对项目评分的不确定性,H值越高表明该项目评分值越不稳定,所以最后考虑H值。据此,本文定义排序准则如下。

定义2(排序准则) 设用户-项目评分矩阵Am×n中有n个项目,Ck(Ek,En,k,Hk)表示第k个项目的分布特征,k=1,…,n。现将所有项目按Ek从小到大依次排列;当Ei=Ej(i,j=1,…,n且i≠j)时,将并列项目按En,k从小到大排列;同理,当En,k相同时,再将并列项目按Hk从小到大依次排列,本文将此视为排列准则。

该准则通过简单排序方法最大化的实现了同质项目集中化、异质项目分散化,完成了项目初次分类,为下一步的相似度计算奠定了基础。基于此,提出本文相似度计算的具体方法:首先,对填充之后的稠密矩阵Am×n,采用式(2)重新计算各个项目的数字特征Ck(Ek,En，k,Hk),k=1,…,n;其次,按照排序准则对所有项目Ck(Ek,En，k,Hk)重新排列,并将排序后的用户-项目评分信息用有序云向量C=(C(1),C(2),…,C(n))来表示;最后,按照式(4)计算相邻项目的云相似度,并将所有项目的相似性指标记作向量S,如式(5)所示。

(4)

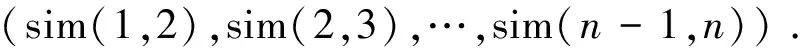
(5)

1.2.2 聚类

聚类分析的实质就是使得类内项目差异尽可能小,类间差异尽可能大的一种分类方法。因此,同一类别内的项目就很可能拥有相同的性质,那么将目标项目纳入某一特定类别就可以为其产生相关推荐。目前,聚类技术已经广泛应用于协同过滤推荐系统中,如K-Means,自组织映射(self-organizingmaps,SOM)等[16]。本文在云模型基础上,采取有序秩聚类算法[15],并将其与K-Means结果进行对比。其具体操作步骤如下:

1) 为项目间相似度进行排秩。将式(5)得到的相似性指标向量S中的所有相似度按照由小及大的原则排秩,即:相似度最小的项秩为1,相似度最大的项秩为(n-1),最终构成相似性指标的秩向量R=(r1,2,r2,3,…,rn-1,n),其中,ri,i+1表示第i个项目的秩。由此可知,秩越小,代表相邻的这两个项目之间差异性越大;秩越大,表明相邻两项目相似性越大。

2) 确定聚类数目k,进行分类。假设我们想将所有样本聚成5类,则就应该将有序云C=(C(1),C(2),…,C(n))在其相似度秩为1,2,3,4(即rij=1,2,3,4)的地方同时断开,这样原始的样本就被分成了5类。同理,如果我们需要将项目聚成k类,则应该在rij=1,2,…,k-1的地方同时断开,这样相邻断点之间的项目就视作一类。

3) 计算每一类的中心。这个聚类的过程可以看作是云聚类,其中每一类别可看做是一个由成百上千个项目云滴组成的云团。因此,每一类的中心完全可以用综合云来代替。令Ct(Et,En，t,Ht)为第t类的综合云数字特征,其中t=1,2,…,k,则第t类的中心可以用式(5)来表示。其中,Nt表示第t类中的项目个数,Et,En，t,Ht分别表示第t类综合项目云的期望、熵、超熵,Eti,En，ti,Hti分别表示第t类中第i个项目的期望、熵、超熵。

(6)

值得注意的是,上述步骤中对项目相似度进行排序时可能会出现相同秩的情形,即:ri,i+1=ri+1,i+2…rj-1,j=rj,j+1(i,j=1,…,n-1且i≠j),此时无法确定该在i还是j处断开时,就需要分别计算在i,i+1…j-1,j等处断开时的分类误差[15],选择使得分类误差达到最小的划分方法作为本文的最终分类决策。

1.3 推荐和预测机制

推荐和预测是协同过滤推荐系统的终极目标。本文提出的方法区别于传统算法,仅仅在目标项目所属的类内寻找邻居,进行推荐。因此,我们首先要计算目标项目与每一类别中心的距离,将其划入合适的类中;下一步就可以进行推荐了。同样借鉴Top-N推荐算法的思想,但仅在目标项目所属的这一类别内选择与其相似度最为接近的N个邻居进行推荐。这一新的算法极大的降低了计算复杂度,缩短了程序运行时间。

预测是根据最近邻居的评分情况来估计目标项目的可能得分的一个过程。众所周知,目标项目与其最近邻居有极大的相似性,但是,即便如此,不同的邻居其相似程度还是有所差异。因此,本文将相似度视为权重对未评分项目进行加权预测,其预测式(7)如下:

(7)

式中：rj表示目标项目Ij的得分；nj为Ij的最近邻居数；sim(i,j)表示目标项目Ij与其第i个邻居Ii的相似性;ri表示项目Ii的评分值。综上所述,将本文提出的基于项目云的有序秩聚类协同过滤推荐算法(ICORC)大致分为三大步,数据处理,有序秩聚类和推荐与预测。其操作步骤可通过流程图1来形象描述。

图1 ICORC算法流程图Fig.1 The flow chart of ICORC algorithm

2 实证分析

2.1 实验设计

为了评估本文提出的方法ICORC的有效性,我们将采用R语言软件在MovieLens数据集(http:∥movielens.umn.edu)上进行试验。该数据集要求每个用户评分项目数至少要20条,其分值从1分到5分不等,分别代表用户对项目不同程度的偏好,“1”表示很不喜欢,“5”表示特别喜欢,稀疏度为93.69%。文中将采用EMA(meanabsoluteerror)和P(Precision)来分别评估预测结果。EMA为平均绝对误差,反映的是样本实际值与预测值之间的绝对偏差,因此EMA值越小越好,如式(8)所示,其中pi,xi分别表示第i个样本的预测值与实际观测值,n为总的样本数。P为预测精确度,如式(9),其中TP(TruePositive)表示预测为推荐项目且实际也是推荐项目的个数;FP(FalsePositive)表示预测为推荐项目,但实际为非推荐项目的个数。因此,P值反映的是预测结果中能正确推荐的比例,其值越大表明推荐精确度越高,推荐效果越好。

(8)

(9)

在本研究中,将呈现通过普通填充由基于云模型的有序秩聚类协同过滤算法(ICORC)获得的结果,以及通过加权填充算法(WICORC)得到的结果,并将其与两个经典的协同过滤算法:基于K-Means聚类的协同过滤算法(KMCF)和基于云模型相似度的协同过滤算法(LICM)进行比较。最终逐一解答以下问题:聚类数K对推荐质量有何影响，最近邻居数N对推荐质量有何影响，ICORC在处理数据稀疏性问题方面是否有效，ICORC是否真的优于传统的CF算法(KMCF,LICM).

2.2 实验结果

图2 聚类数K对推荐结果的影响Fig.2 The influence of cluster number K for recommend result

通过MovieLensdataset实验结果可知,见图2,随着聚类数目的增加,EMA值呈大幅度降低的趋势,当聚类数K=15时,EMA值已经很小,之后EMA值呈现较为平缓的趋势。由图3可以看出,随着最近邻数目的增加,EMA的趋势变化较为平缓,且当最近邻居数目N>15时,EMA值基本不再变化。因此,当聚类数K=15,最近邻居数N=15时,EMA值降到稳定状态,推荐结果达到最优。

图3 邻居数N对推荐结果的影响Fig.3 The influence of neighbor number N for recommend result

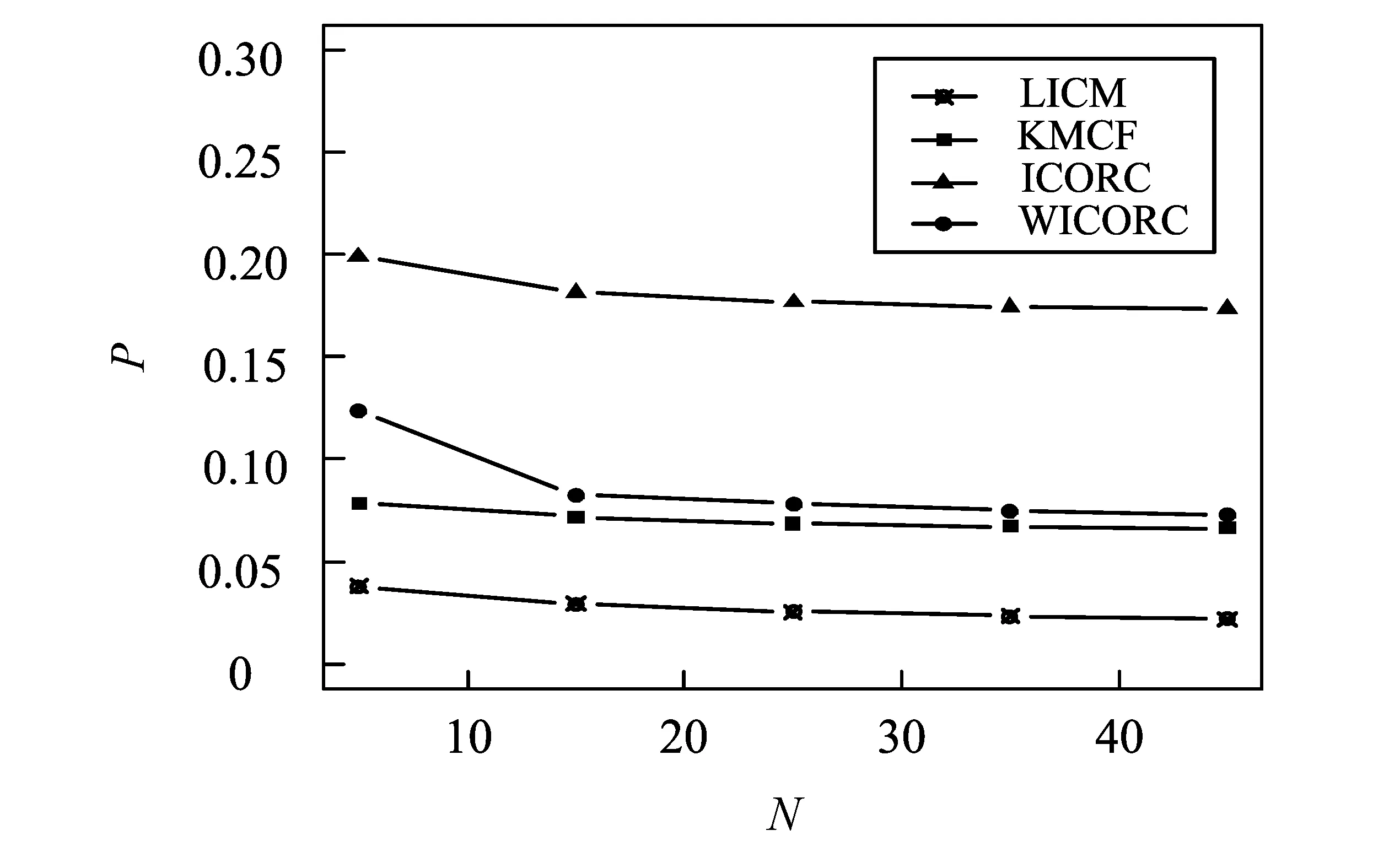
图4 邻居数N对预测精确度的影响Fig.4 The influence of neighbor number N for precision

对比四种算法(KMCF,LICM,ICORC,WICORC),综合图2-图4可以看出,无论聚类数目,最近邻居数如何变化,ICORC都具有最小的EMA和最大的P值。因此认为ICORC推荐效果更优。且就P值而言,ICORC与WICORC算法都优于传统的LICM和KMCF算法,原因就在于ICORC算法综合考虑了用户评分随机性、模糊性等特点,最大限度地挖掘用户评分信息,获取每个项目的近似分布,进而去填充原始稀疏矩阵,既保留了原始矩阵的评分特征,又缓解了推荐中的冷启动问题,因此ICORC算法在数据稀疏性问题上比传统的LICM和KMCF算法有更好的预测效果。

3 总结及发展前景

笔者从一个全新的视角出发,借鉴定性分析与有序秩聚类的思想,提出了一种新型的基于项目云的有序秩聚类的协同过滤推荐算法,并将这一算法同传统的KMCF和LICM算法在MovieLensdata集上做比较。实验表明,较于传统的协同过滤算法该方法有两大优势。

1) 该算法从定性分析的层面考虑,由于不同的用户其评分偏好在某种程度上一定存在差异性,因此引入项目云来填充缺失数据,不仅能较好地解释用户在选择项目时的随机性,以及用户评分的不确定性、模糊性,而且能克服数据的稀疏性,同时高度还原原始评分矩阵中所含信息的特征。

2) 该算法依据每个项目评分值的分布特征进行有序秩聚类,并在类内寻找项目“邻居”,区别于传统的计算所有项目的相似度的聚类算法,该算法仅需要计算拥有相似特征的相邻项目间的相似性,其计算时间复杂度为o(n),而传统算法计算相似度的时间复杂度为o(n2)。因此,该算法不仅能够缓解数据稀疏性以及冷启动问题,提高推荐精度,而且能大量节省时间。尤其是对于高维大数据,ICORC算法的优势就更为明显。

在本文的研究中,尽管我们对原始数据的稀疏性进行了很大的改善,而且在某种程度上极大的减少了EMA,提高了P值,但依然有许多问题亟需解决。首先,本文没有充分考虑到用户之间的潜在关系;其次,在推荐过程中,本文也没有考虑推荐数目对推荐精度的影响,从理论上来讲,应该是推荐数目越多,推荐精度越高。因此,未来我们可以考虑从这几个方向去做深入研究:分析影响用户评分的因素;或者探索用户评分值的真实分布。另外,进一步提高协同过滤推荐系统的推荐精度以及计算速度仍是我们需要努力的方向。

[1]XURZ,WANGSQ,ZHENGXW,etal.Distributedcollaborativefilteringwithsingularratingforlargescalerecommendation[J].TheJournalofSystemsandSoftware,2014,(95):231-241.

[2]GOLDBERGD,NICHOLSD,OKIBM,etal.Usingcollaborativefilteringtoweaveaninformationtypestry[J].CommunACM,1992,35(12):61-70.

[3]RENSICKP,IACOVOUN,SUCHAKM,etal.GroupLens:anopenarchitectureforcollaborativefilteringofnetnews[C]∥ACM.Proceedingsofthe1994ACMConferenceonComputerSupportedCooperativeWork(CSCW)UnitedStates：NorthCarolina,1994:175-186.

[4]SARWARB,KARYPISG,KONSTANJ,etal.Item-basedcollaborativefilteringrecommendationalgorithms[C].Proceedingsofthe10thinternationalconferenceonWorldWideWeb.HongKong:ACM,2001:285-295.

[5]CECHINELC,SICILIAM,SALVADORSA,etal.Evaluatingcollaborativefilteringrecommendationsinsidelargelearningobjectrepositorise[J].InformationProcessingandManagement,2013(49):34-50.

[6] 孙小华.协同过滤系统的稀疏性与冷启动问题研究[D].杭州:浙江大学,2005.

[7]HUANGZ,CHENH,ZENGD.Applyingassociativeretrievaltechniquestoalleviatethesparsityproblemincollaborativefiltering[J].ACMTransInformationSystems,2004,22(1):116-142.

[8]WENGLT,XUY,LIY,etal.Exploitingitemtaxonomyforsolvingcold-startprobleminrecommendationmaking[C].Proceedingsofthe20thIEEEInternationalConferenceonToolswithArtificalIntelligence,Dayton,USA,2008:113-120.

[9]BACKSTROML,LESKOVECJ.Supervisedrandomwalks:predictingandrecommendinglinksinsocialnetworks[J].ComputerScience,2011(11):635-644.

[10]CAIY,LEUNGHF,LIQ,etal.Typicality-basedcollaborativefilteringrecommendation[J].IEEETrans.KnowledgeandDataEng,2014,26(3):766-779.

[11] 张光卫,李德毅,李鹏.基于云模型的协同过滤推荐算法[J].软件学报,2007,18(10):2403-2411.

[12] 余志虎,戚玉峰.一种基于云模型数据填充的算法[J].计算机技术与发展,2010,20(12):34-37.

[13] 孙金刚,艾丽蓉.基于项目属性和云填充的协同过滤推荐算法[J].计算机应用,2012，32(3):658-660.

[14] 王国胤,李德毅,姚一豫，等.云模型与粒计算[M].科学出版社，2012(inChina).

[15] 朱建平,方匡南.有序秩聚类及对地震活跃期的分析[J].统计研究,2009，26(1):83-87.

[16]TSAICF,HUNGC.Clusterensemblesincollaborativefilteringrecommendation[J].AppliedSoftComputing,2012(12):1417-1425.

(编辑：朱 倩)

Application of Ordered Rank Cluster in Recommendation Systems Based on Item Cloud

DU Zongyan,JING Yingchuan

(College of Mathematics, Taiyuan University of Technology, Jinzhong Shanxi 030600, China)

In order to further improve recommender accuracy, in this paper we propose a novel ordered rank cluster in collaborative filtering based on the item cloud (ICORC) method, which includes three steps: data processing, ordered rank clustering, and recommendation generating. This method has two advantages. One is that it can tackle the data sparsity problem by filling in missing data using the item cloud. Another distinct feature is that it can save time and obtain more accuracy through finding “neighbors” of items among the clusters, which are formed by sorting, partition and clustering for the numerical characteristics of item distribution. To the best of our knowledge, there has been no prior work on investigating CF recommendation by combining ordered rank cluster.We conducted this experiment on the MovieLens datasets and found that ICORC is superior to other collaborative filtering (CF) algorithms on the mean absolute error and Precision.

collaborative filtering;cloud model;ordered rank cluster;rating reliability;recommender system

1007-9432(2016)05-0673-07

2015-10-06

国家自然科学基金资助项目：高维数据变量间非线性交互作用的研究(11571009)

杜宗宴(1990- )，女，山西孝义人，硕士，主要从事数理统计及数据挖掘方向的研究，(E-mail)duzongyan908@126.com

景英川，副教授，主要从事数理统计及数据挖掘方向的研究，(E-mail)shyjyc1970@163.com,

F224;F713.36

A

10.16355/j.cnki.issn1007-9432tyut.2016.05.021