结构规范计算公式与经典力学理论的比较

夏广印，徐勤花

（中集海洋工程研究院有限公司，山东烟台 264670）

结构规范计算公式与经典力学理论的比较

夏广印，徐勤花

（中集海洋工程研究院有限公司，山东烟台 264670）

对于结构规范的计算公式与经典力学的计算看起来有很大差别，但二者本质上是一样的。文章主要概述了国际知名船级社DNV和ABS的规范计算公式与经典力学的理论基础以及推导过程。从规范公式来源以及各参数取值上深入探讨其根本目的，有助于工程师利用好规范，而又高于规范。

深舱；支反力；跨矩；抗弯截面系数

0 引言

船舶与海洋工程结构的力学来源于经典力学，但是，它又有其特定条件。随着技术的发展，各船级社都在船舶与海洋工程结构的基础上，研究出了各自的经验公式。通常情况下，应用这些技术的工程技术人员难以从根源上找到这些公式参数的真正含义，就无法灵活应用。本文作者在查阅了大量相关文献的基础上，结合多年的结构设计经验，尝试从理论和实践来寻求经验力学与结构规范计算公式的来源及推导过程。

1 概述

目前无论是ABS，还是DNV，进行规范公式计算都有几个前提条件：1）梁系受力是均布载荷；2）板架理论；3）梁的两端固支。本文将分别讨论这几个前提条件。

1.1 规范计算的简化基础和均布载荷

第一个前提条件是均布载荷。对船舶来说，主要承受的是液体的压力，包括外部的海水压力、内部舱室的液体传递的压力。无论哪一种压力，都是均布载荷分布。如果不是均布载荷，就需要把对应的力学模型与均布载荷进行比较分析。

根据经典力学的梁的理论，梁的受力模型如图1所示[1]，图中，O为坐标原点；x为梁的轴向，z为梁的载面方向；l为梁的长度；Q为整个梁上受到的均布载荷的总和。

图1 整个跨度受均布载荷

特定要素主要指两端支反力、两端弯矩、中间弯矩、最大形变等特定的力学数据。

式中，R1和R2分别为两端的支反力；Q为整个梁上承受的均布载荷的总和；M为梁上承受的弯距；l为梁的跨距；x为梁距离一段的距离；B为梁的柔性量度，B=l3/EI；v为梁的最大变形量。

从图1中可以看出最大弯距和最大剪力都在两端。最大变形在梁的中间。最大弯距M=Ql/12，最大剪力R=Q/2，最大变形v=QB/384。

1.2 板架理论和梁的两端固支

船体结构由图2[1]所示的板架结构组成，其中每个小的板格长度方向为扶强材，而宽度方向上为强梁。

在图2(b)中，板格mnkl上的均布载荷如果为q，则认为短边lm和nk上承受的力为，而长边mn和kl上承受的力为。如果a/b很小，比如小于1/2，为了计算方便，通常把短边承受的力略去，就成了长边承受的力qab/2。然后把一个个小的板格上的力扩展到整个 L×l板架上，则沿 l方向的构件在两个梁之间承受的力为qab，这样构件 mn或 kl上承受的最大弯距M=qab2/12，最大剪力F=qab/2。而沿L方向的单根梁承受的力学模型如图3所示。

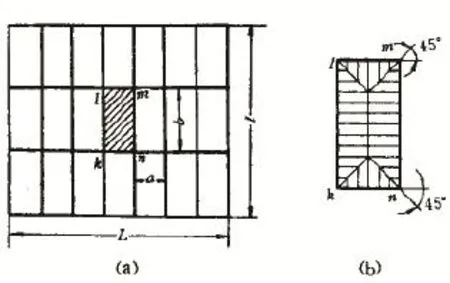
图2 板架结构示意图

图3 单根梁简化力学模型

从图3可以看出，相当于承受N个集中力加上均布载荷的梁。这些力的和为qbL，它处于中间集中力qbL的弯距和整个跨度内承受均布载荷qbL的梁的弯距之间。为了方便计算，实际运用时，取弯距；最大剪力F=qbL/2。图4比较了当N=4，q=10，a=0.60，b=2.40，L=3.00时的情况。图4(a)为四个集中力14.4的情况，图4(b)为均布载荷的情况。

从两个力学模型中可以看出，在图4(a)中，最大的剪力Fa=28.8，最大的弯距Ma=17.3。而在图4(b)中，最大的剪力Fb=36，最大的弯距Mb=18。如果用前面的公式计算出的结果为：M=21.6，F=36。因此，实际简化后的结果都比计算公式得出的结果要小。而在工程应用上，这种方法是保守的可靠性设计，是符合工程实际的。

而对于上面的板材，可以取a×a的一个小板格，则这个板格中板承受的力为：qa2/2，另一半的力由两侧的梁来承受。简化后的最大弯距M=qa3/24，最大剪力F=qa2/4。简化成均面载荷计算和实际的模型比，如图5所示。所有参数的取值和图4一样。

从图5可以看出，两种力学模型中的最大剪力和最大弯距都是F=0.9，M=0.1。因此这种简化是可行的。

图4 不同载荷分布形式下梁受力示意图

图5 实际力学模型与简化为均布载荷的力学模型对比

2 DNV规范公式

以钢质船规为例进行推导。

2.1 对于板材

对于板材，DNV规定最小板厚的公式[2]如下：

式中，t为规范要求的最小板厚，mm；ka为板格长宽比修正系数，如果长宽比小于2.5，由于不符合前面的假设条件，所以要进行修改。如果不小于2.5，ka=1；s为型材间距，即前面提到的板格的短边长度，m；p为设计压力，kN/m2；σ为材料的许用应力，N/mm2；tk为腐蚀余量，mm。

然后，对此公式进行推导，过程如下：

弯曲应力校核：板格s×s的范围承受最大弯距

由前面的论述可以得到：

因此所需的最小抗弯截面系数（通常也叫作剖面模数）为：

而板厚为t、宽为s的矩形板的抗弯截面系数为：

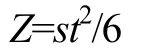
由式(6)和(8)可以得出：

由于式(9)是基于前面的假设得出的，所以当这种假设不成立时，需要有个长宽比修正系数ka。同时，船舶在海上有腐蚀的问题，所以需要加上腐蚀余量tk，就得到了DNV规范规定的板材计算公式。

2.2 对于扶强材

对于扶强材，DNV规范规定的最小剖面模数的计算公式[2,3]为：

式中，l为扶强材的跨距，m；s为扶强材的支撑宽度，m；p为扶强材的承受的压力，kN/m2；wk为压载舱腐蚀系数，其它位置为1.0。在这里不讨论这个系数，只讨论其它位置为1.0的情况；σ为材料的许用应力，N/mm2。

根据前面讨论的经典力学模型，梁承受的最大弯距为：

所需要的最小剖面模数为：

不考虑压载舱腐蚀系数，就和DNV规范公式完全一样了[4]。

2.3 对于强梁

对于强梁，DNV规范规定其所需的最小剖面模数[2,5]为：

式中，S为梁的跨距，m；b为梁支撑宽度，m； p为扶强材的承受的压力，kN/m2；wk为压载舱腐蚀系数，其它位置为1.0。在这里不讨论这个系数，只讨论其它位置为1.0的情况；σ为材料的许用应力，N/mm2。

根据前面的经典力学讨论。梁承受的最大弯距为：

梁所需要的最小剖面模数为：

DNV规范规定了强梁端部所需要的最小受剪面积[2]为：

式中，k为系数，根据位置不同取0.6～0.8；S、b、p、tk与前面的定义相同；f1为材料系数，如果为普通钢，则f1=1；h为梁的腹板高度，m。

根据前面的板格理论，强梁端部的剪力为：

如果只考虑剪切应力，材料系数Sa=2.5，普通钢的屈服强度Òs=235 MPa。同时还要考虑允许不超过腹板高度1/4的开孔。因此通常情况下允用剪切应力τ=70.5 MPa。

根据式(17)，在不考虑腐蚀余量的情况下，强梁所需要的最小受剪面积为：

如果根据位置的不同，引入系数k，再加上腐蚀余量，就成了前面的DNV公式。

3 ABS规范公式

以钢质船规为例进行推导。

3.1 对于板材

对于板材，ABS规定最小板厚的公式[6]如下：

式中，s为型材间距，mm；k为长宽比修正系数，当长宽比大于2时，k=1；q为材料系数，普通钢取1，其余的材料，其中σs为材料的屈服强度，N/mm2；h为设计压头，m，是指的水柱的

高度，1 m水注相当于压力为9.81 kN/m2的压强；c为系数，对液舱取254，对空舱和上建取290；tk为腐蚀余量，mm。

板格s×s的范围承受最大弯距由前面的论述可以得到：

因此所需要的最小抗弯截面系数（通常也叫剖面模数）为：

而板厚为t，宽为s的矩形板的抗弯截面系数为：

由式(21)和式(22)可以得出：

ABS规范的理论基础是，板是第一道防线，材料系数最小。如果板坏了，力由扶强材承受。扶强材作为第二道防线，强梁是最后一道防线，因此强梁的材料系数是最大的。对于深舱内的板材，材料系数Sa=1.43；对于空舱和上建，材料系数为Sa=1.1。对于深舱，允许应力σ=164 N/mm2；对于其他位置，σ=214 N/mm2；

把许用应力代入式(23)可以得出：

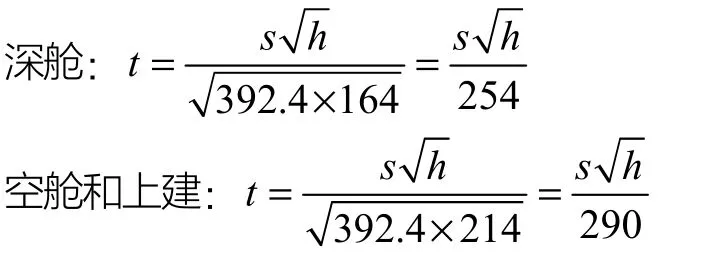
考虑材料系数、腐蚀余量和板格的比例系数，就得到了ABS规范的板材的计算公式。

3.2 对于扶强材

ABS规范规定的扶强材的计算公式[6]为：

式中，c为边界支撑条件系数，当两边为强梁支撑时取1.00，其余有肘板或更有效的支撑时可以折减；h为设计压头，m，是指水柱的高度，1 m水注相当于压力为9.81 kN/m2的压强；s为型材间距，m；l为扶强材的跨距，m。

根据前面讨论的经典力学模型，梁承受的最大弯距为：

所需要的最小剖面模数为：

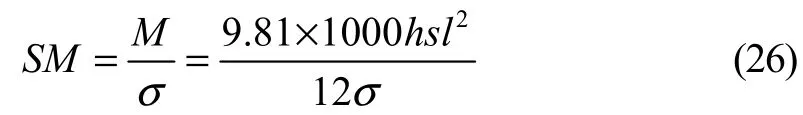
由于需要考虑腐蚀余量和材料系数，所以扶强材材料的允许用应力为：

代入式(26)可以得到：

考虑边界条件系数c，就可以得到ABS的扶强材规范公式。

3.3 对于强梁

对于强梁，ABS规范规定其需要的最小剖面模数[6]为：

式中，c为位置系数，对深舱取1.5，对空舱或上建取1.0；h为设计压头，m，是指水柱的高度，1 m水注相当于压力为9.81 kN/m2的压强；s为型材间距，m；l为扶强材的跨距，m。

根据前面讨论的经典力学模型，梁承受的最大弯距为：

所需要的最小剖面模数为：

由于需要考虑腐蚀余量和材料系数，所以深舱中强梁材料的许用应力为：

空舱和上建中强梁材料的许用应力[7]为：

代入式(29)可以得到：

Comparison of Calculating Formula for Structure Rule with Classical Theory of Mechanics

Xia Guang-yin, Xu Qin-hua
(Yantai CIMC Raffles Offshore Ltd., Shandong Yantai 264670, China)

The calculating formula for the structure rules looks very different from the classical theory of mechanics.However, they are the same on the principle.The paper introduces the theoretical foundation of the rule calculating formula of the famous classification societies of DNV and ABS and the classical theory of mechanics, as well as the derivation process.It deeply discusses the purpose from the rule formula source and the date of the parameters.It helps the structural engineers use class rules better and they can understand on a higher level than the rules.

deep tank; force act on the backstop; span; section module

U661.4；U662.1

A

10.14141/j.31-1981.2016.02.003

夏广印（1977—），男，硕士，高级工程师，研究方向：船舶与海洋工程。