用样本估计总体的三种题型

文/于宗英 王 琦

用样本估计总体的三种题型

统计的基本思想是用样本估计总体，即用部分来推断整体，从而做出正确的决策.在2016年的中考试题中,用样本估计总体有以下三种题型.

一、用样本的分布估计总体的分布

例1（2016年临沂卷）为了解某校九年级学生的身高情况，随机抽取部分学生的身高进行调查，利用所得数据绘成如图1的统计图表.

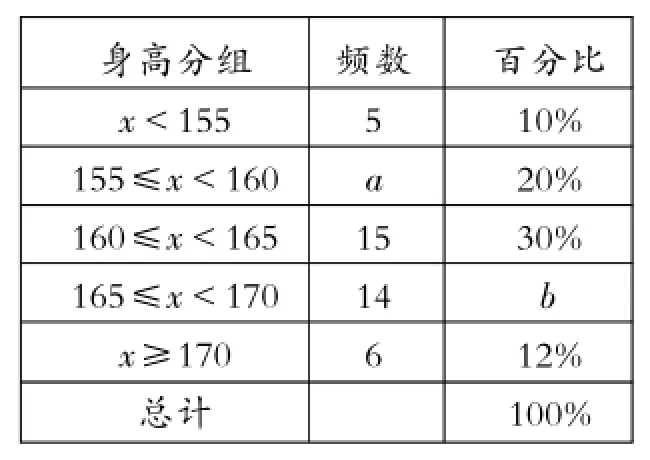
频数分布表

图1

图2

（1）填空：a=，b=；

（2）补全频数分布直方图；

（3）该校九年级共有600名学生，估计身高不低于165cm的学生大约有多少人？

解：（1）总人数为5÷10%=50，

∴a=50×20%=10，

b=14÷50×100%=28%.

（2）补全的频数分布直方图如图2.

（3）600×（28%+12%）=240（人）.

二、用样本的数字特征估计总体的数字特征

例2（2016年阳泉卷）甲、乙两台机床生产同种零件，10天出的次品个数分别是：

甲：0，1，0，2，2，0，3，1，2，4乙：2，3，1，1，0，2，1，1，0，1

分别计算两台机床生产零件出次品的平均数和方差，根据计算估计哪台机床的性能较好.

解：甲机床出次品的平均数=（1+2+2+3+1+2+4）÷10=1.5；=[（0-1.5）2+（1-1.5）2+（0-1.5）2+（2-1.5）2+（2-1.5）2+（0-1.5）2+（3-1.5）2+（1-1.5）2+（2-1.5）2+（4-1.5）2]÷10=1.65；

乙机床出次品的平均数=（2+3+1+1+2+1+1+1）÷10=1.2；=[（2-1.2）2+（3-1.2）2+（1-1.2）2+（1-1.2）2+（0-1.2）2+（2-1.2）2+（1-1.2）2+（1-1.2）2+（0-1.2）2+（1-1.2）2]÷10=0.76.

三、综合利用图表信息估计总体

例3（2016年娄底卷）在2016CCTV英语风采大赛中，娄底市参赛选手表现突出，成绩均不低于60分．为了更好地了解成绩分布情况，随机抽取了200名学生的成绩（成绩x取整数，总分100分）作为样本进行了整理，得到如图3的两幅不完整的统计图表.

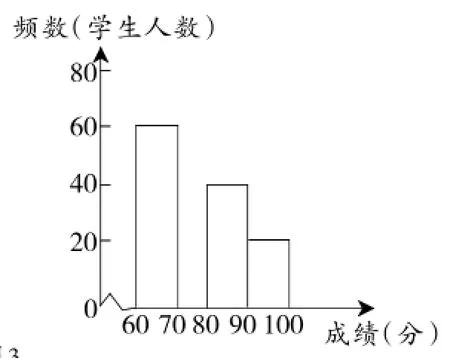
图3

图4

根据所给信息，解答下列问题：

（1）在频数分布表中，m=，n=；

（2）请补全图中的频数分布直方图；

（3）按规定，成绩在80分以上（包括80分）的选手进入决赛．若娄底市共有4000人参赛，请估计约有多少人进入决赛.

解：（1）m=200×0.40=80（人），n=40÷200=0.20.

（2）根据（1）可得，成绩在70≤x＜80的人数有200-60-40-20=80人，补全的频数分布直方图如图4所示.

（3）进入决赛的约有：4000×（0.20+0.10）=1200（人）．

责任编辑：王二喜