解锐角三角函数题的常见错误

文/李月恬

解锐角三角函数题的常见错误

在解答锐角三角函数题时，同学们要注意避免以下错误．

一、锐角三角函数的概念不清

例1（2016年金华卷）一座楼梯如图1所示，BC是铅垂线，CA是水平线，BA与CA的夹角为兹．现要在楼梯上铺一条地毯，已知CA=4米，楼梯宽度1米，则地毯的面积至少需要（）

图1

错解：在Rt△ABC中，

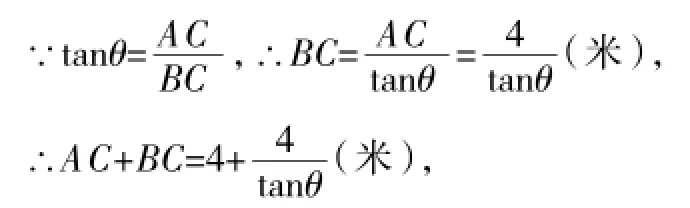
错因诊断：角兹的正切等于对边比邻边．

∴AC+BC=4+4tan兹（米），

∴地毯的面积至少需要1×（4+4tan兹）=4+4tan兹（米2）.选D．

温馨小提示：正弦、余弦、正切都是研究直角三角形中锐角与两边比值的关系，已知其中的两个量，就可求出第三个量．

二、误认为直角三角形中∠C一定是直角

例2（2016年兰州卷）在Rt△ABC中，∠B越90°，sinA越，BC越6，则AB越（）

A.4.B.6.C.8.D.10.

错因诊断：因为∠B=90°，所以AC为斜边.

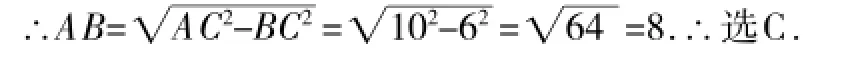
温馨小提示：在解题时要认真审题，分清斜边和直角边，以防出错.

三、混淆了正弦（正切）与余弦函数的增减性

A．30°＜琢＜45°.B.45°＜琢＜60°.

C．60°＜琢＜90°.D.30°＜琢＜60°.

错因诊断：当琢为锐角时，正弦和正切值随着角度的增大而增大，余弦值随着角度的增大而减小．

故45°＜琢＜60°．选B．

温馨小提示：要熟记三种三角函数的增减性和特殊角的三角函数值．

四、未说明直角三角形就应用三角函数的概念解题

例4（2016年威海卷）如图2，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（）

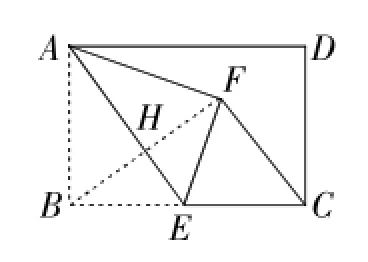
图2

错解：连接BF.疫BC=6，点E为BC的中点，亦BE=3，

错因诊断：用三角形边的比表示锐角的正弦、余弦和正切的前提是在直角三角形中，必须先证明△BCF是直角三角形,才能应用三角函数的概念来解题.

正解：连接BF，疫BC=6，点E为BC的中点，亦BE=3，又∵AB=4，∴AE=由折叠可知，AE垂直平分BF，又∵∠ABE=90°，亦∠CBF=∠BAE，∴sin∠CBF=

∵FE=BE=EC，亦∠BFC=90°，∴sin∠CBF=选D.

温馨小提示：在应用三角函数概念解题时，一定是在直角三角形中，若不是直角三角形，则需证明或构造出直角三角形.

五、在非直角三角形中应用锐角三角函数求值

例5（2016年福州卷）如图3，6个形状、大小完全相同的菱形组成网格，菱形的顶点称为格点.已知菱形的一个角（∠O）为60°，A，B，C都在格点上，则tan∠ABC的值是．

错解：设菱形的边长为a，则AC=2a.由题意∠O=60°，可知BC=a，∴

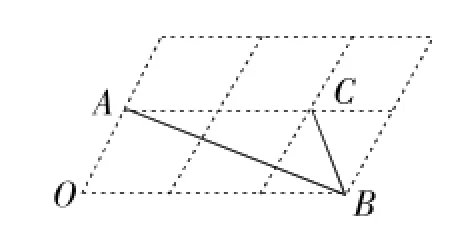
图3

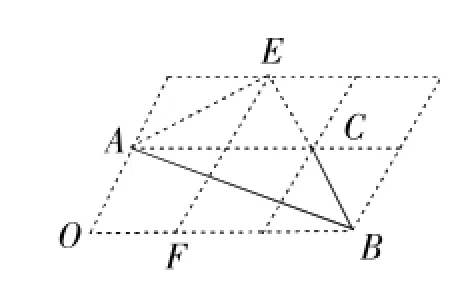
图4

错因诊断：锐角三角函数是在直角三角形中定义的,但△ABC显然不是直角三角形，必须将∠B放在直角三角形中，才能应用锐角三角函数的知识来求解.

正解：如图4，连接EA，EC，设菱形的边长为a，由题意

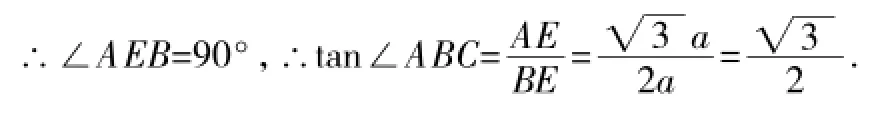
温馨小提示：在非直角三角形中，不能直接用三角函数的概念求值.网格中，格点图形的角度、边长都可利用勾股定理计算出来，这是隐含条件，要充分利用.

六、思考问题不全面而漏解

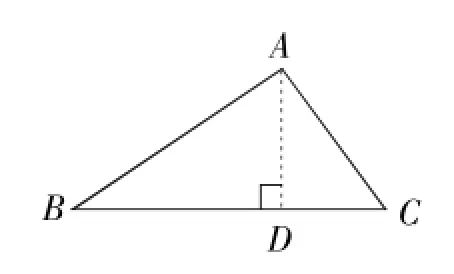
图5

图6

错解：如图5，设CD越x，由BD∶CD越2∶1得BD越2x，BC越BD垣CD越3x越6，解得x越2，BD越4.

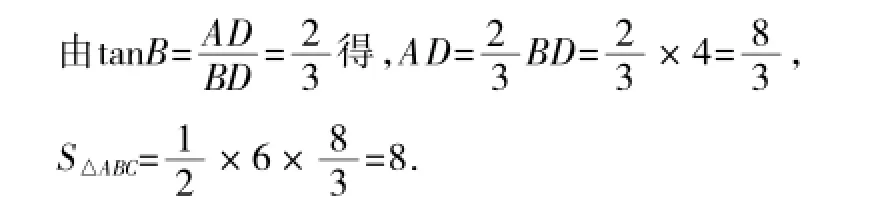
错因诊断：高AD不一定在△ABC的内部，应分两种情况：（1）高AD在△ABC内部；（2）高AD在△ABC外部.错解没有考虑第（2）种情况.

正解：设CD越x，由BD∶CD=2∶1得BD越2x.（1）若高AD在△ABC的内部，如图5，解法同上；（2）若高AD在△ABC的外部，如图6，BC越BD原CD越x越6，BD越12，由tanB越故△ABC的面积为8或24．

温馨小提示：对于没有确定三角形高的位置的“涉高”问题，要对高的位置分类讨论，谨防漏解.

七、忽视三角函数值的取值范围

例7已知锐角A满足关系式2sin2A-7sinA+3越0，则sinA的值为．

错解：由2sin2A-7sinA+3越0，即（sinA-3）（2sinA-1）＝0．

∴sinA-3越0或2sinA-1越0，即sinA越3或sinA越

错因诊断：由于A为锐角，所以本题隐含着0＜sinA＜1，0＜cosA＜1的条件，因此sinA越3应舍去，只有一个值sinA越．（正解略）.

温馨小提示：对于锐角三角函数有结论：（1）sin2A+cos2A=1（平方关系），tanA=商的关系）；（2）0＜sinA＜1，0＜cosA＜1（正弦和余弦的有界性），tanA＞0（正切的非负性）．

责任编辑：王二喜