解直角三角形的应用
2016-12-13严云海
文/严云海
解直角三角形的应用
文/严云海
解直角三角形的应用是锐角三角函数的重要内容.近年来运用解直角三角形的知识解决与生活相关的应用题成为中考命题的热点.解题的关键是建立数学模型,把实际问题转化为数学问题求解.下面以2016年中考题为例,归纳这类问题的解法.
解直角三角形涉及各种图形,熟悉基本图形及其对应线段之间的关系是解题的前提.
一、基本图形
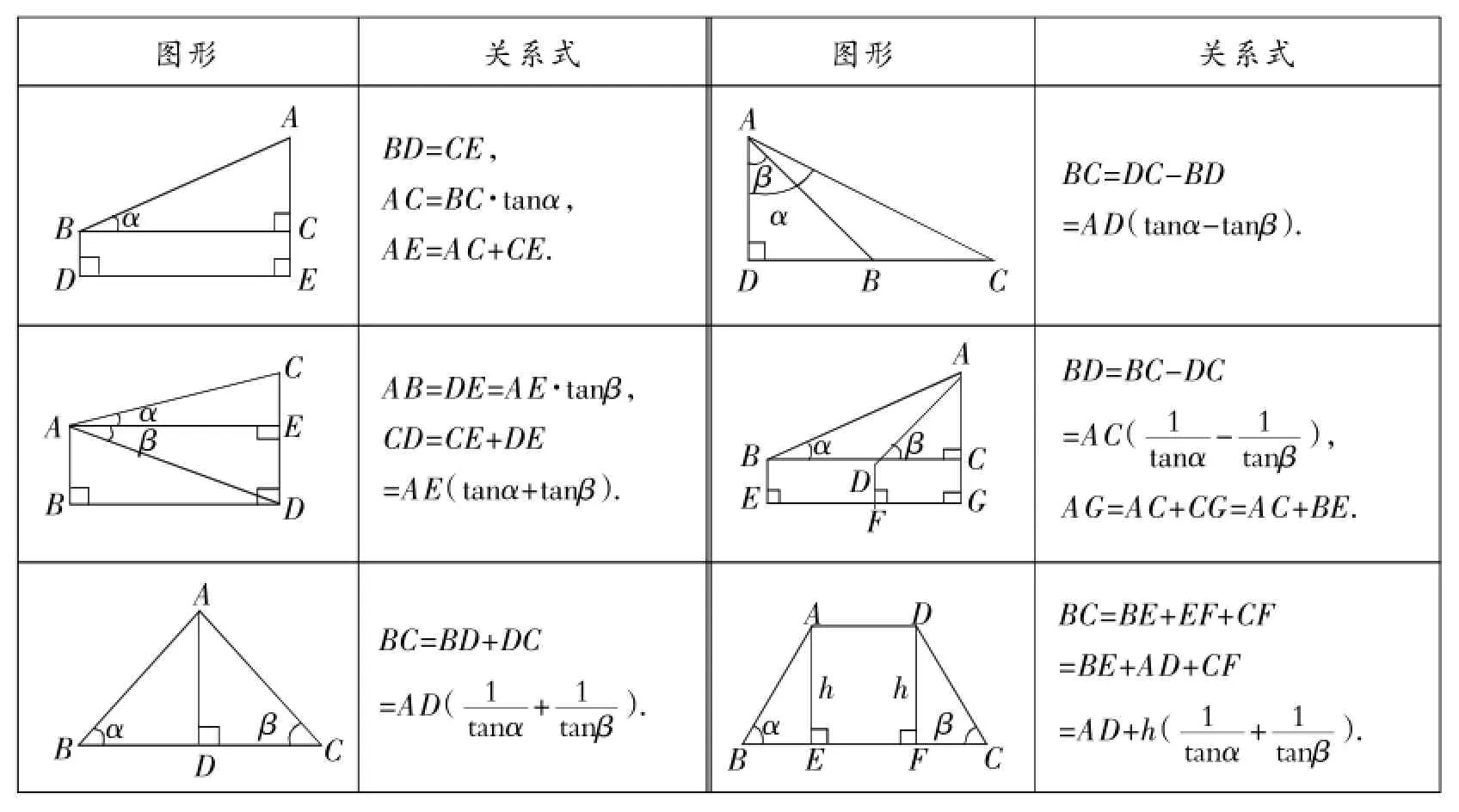
二、典型应用
1.仰角、俯角问题
例1(2016年昆明卷)如图1,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边沿点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=80m,DE=10m,求障碍物B,C两点间的距离(结果精确到0.1m.参考数据:≈1.414,≈1.732).
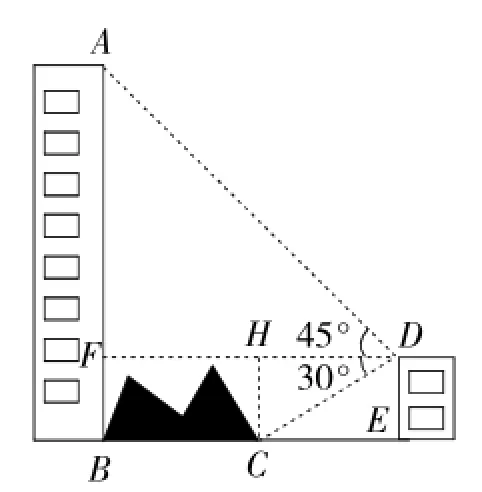
图1
分析:如图1,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H援解Rt△AFD可得到DF的长度,解Rt△DCE可得到CE的长度,则BC=DF原CE援
解:如图1,过点D作DF⊥AB于点F,过点C作CH⊥DF于点H,则DE=BF=CH=10m.
在Rt△ADF中,疫AF=80m-10m=70m,∠ADF=45°,∴DF=AF=70m.
在Rt△CDE中,疫DE=10m,∠DCE=30°,

答:障碍物B,C两点间的距离约为52.7m.
方法归纳:仰角、俯角问题通常涉及多个仰角或俯角,解题时,利用三角函数的定义分别在仰角或俯角所在的直角三角形中求出相应线段的长度,从而求解.当题中的关系比较复杂时,可先设未知数,用同一个未知数表示问题中不同的量,列方程求解.
2.坡度、坡角问题
例2(2016年济宁卷)某地的一座人行天桥如图2所示,天桥高为6米,坡面BC的坡度为1∶1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1∶
(1)求新坡面的坡角琢;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.

图2
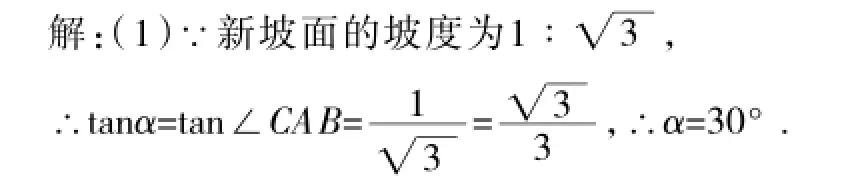
答:新坡面的坡角琢为30°.
(2)文化墙PM不需要拆除.理由如下:
过点C作CD⊥AB于点D,则CD=6.

∴文化墙PM不需要拆除.
方法归纳:解答这类问题,需要作高构造直角三角形.根据坡比的定义,将坡比转化为线段的长度比是解题的关键.
3.方位角问题
例3(2016年常德卷)南海是我国的南大门.如图3所示,某天我国一艘海监执法船在南海海域进行常态化巡航,在A处测得北偏东30°方向上、距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只.问:我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
(参考数据:cos75°=0.2588,sin75°=0.9659, tan75°=3.732,=1.732,=1.414)

图3
分析:过B作BD⊥AC,在Rt△ABD中,可求出BD与AD的长,在Rt△BCD中,可求出CD的长,从而求出AC的长.
解:过B作BD⊥AC,
疫∠BAC=75°-30°=45°,
∴在Rt△ABD中,∠BAD=∠ABD=45°,∠ADB=90°,

答:我海监执法船在前往监视巡查的过程中行驶了67海里.
方法归纳:要掌握方位角的表示方法,将实际问题抽象成数学问题,转化为解直角三角形.当不是直角三角形时,通过作高转化为直角三角形求解.
4.其他问题

图4
例4(2016年山西卷)太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业.如图4是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm.求:支撑角钢CD和EF的长度各是多少cm(结果保留根号)?
分析:过A作AG⊥CD于G,在Rt△ACG中,求得CG=25,连接FD并延长与BA的延长线交于H,在Rt△CDH中,根据三角函数的定义得到CH=90,在Rt△EFH中,根据三角函数的定义即可得到结论.
解:过A作AG⊥CD于G,则∠CAG=30°.
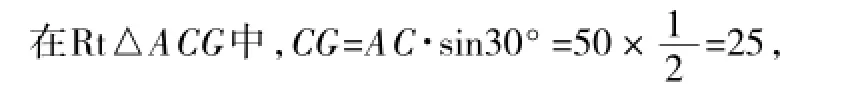
∵GD=50-30=20,∴CD=CG+GD=25+20=45.
连接FD并延长与BA的延长线交于H,则∠BHF=30°,
∴EH=EC+CH=AB-BE-AC+CH=300-50-50+90=290,

方法归纳:这类问题的背景往往是某一个生活用品(或其剖面图),文字较长,概念较多,解题时,要边阅读题干边看图形,将实物(或剖面图)抽象成数学图形求解.
责任编辑:王二喜
