基于Burg算法功率谱估计的参数选择

黄 超，王 伟，单 凉

(电子工程学院，合肥 230037)



基于Burg算法功率谱估计的参数选择

黄 超，王 伟，单 凉

(电子工程学院，合肥 230037)

介绍了现代功率谱估计中常用的基于自回归(AR)模型的Burg算法，分析了Burg算法中参数选择对功率谱估计的影响，并给出综合最优的Burg算法参数选择方法，最后将本文参数选择方法应用于列车测速系统进行实验验证，准确地估计出了列车的多普勒频率。

功率谱估计；自回归模型；Burg算法；参数选择

0 引 言

在现代信号处理中，对于具有各态历经性的平稳随机信号很难用数学关系式来清楚地描述。为了分析平稳随机信号，可以利用采集的N个样本数据来估计该信号的功率谱密度(PSD)，这种方法就被称为功率谱估计[1-3]。功率谱估计常被应用于许多实际问题中，例如雷达信号处理和生物医学工程等。一般来说, 功率谱估计方法可分为两大类：经典谱估计法(非参数估计法)和现代谱估计法(参数估计法)。经典谱估计法分为直接法和间接法，均是以数字傅里叶变换(DFT)为基础，具有分辨率低、频谱混叠等固有缺点。现代谱估计法先建立功率谱估计模型，然后利用观测数据对建立的模型进行参数估计，最后完成功率谱估计。该方法分辨率很高，拥有比经典谱估计法更好的参数估计性能。

目前常用的功率谱估计模型有自回归(AR)模型、滑动平均(MA)模型和自回归滑动平均(ARMA)模型[4]。其中，AR模型是现代谱估计中最常用的一种功率谱估计模型，这是因为AR模型的实际物理系统是全极点系统；而且该模型的参数估计算法是线性方程组，运算量较小，计算比较简便。在基于AR模型进行功率谱估计时，必须先提取出AR模型的参数。目前这些参数的提取算法主要有Levinson-Durbin算法[5]、Burg算法[6-7]和Marple算法[8]3种。其中，Levinson-Durbin算法的复杂度最低，而且能够保证预测误差滤波器最小相位，但是分辨率较低；Marple算法分辨率很高，性能最好，但是对硬件要求较高，计算量较大；Burg算法分辨率较高，计算也不太复杂，综合性能最好，常常被用来进行功率谱估计。

基于Burg算法对实际工程问题进行功率谱估计时，如何构建适合实际问题的Burg算法参数模型至关重要。本文首先通过MATLAB分析采样频率、采样点数、AR模型阶数和快速傅里叶(FFT)长度等Burg算法参数对功率谱估计的影响，并给出综合最优的Burg算法参数选择方法，最后采用列车测速系统的实验数据进行仿真验证。

1 基于Burg算法的功率谱估计

1.1 基于AR模型的功率谱估计

AR模型又称为自回归模型,是一个全极点的模型,可用如下差分方程来表示:

(1)

式中：p为AR模型的阶数；{a(k)|k=1,2,…,p}，为p阶AR模型的参数。

将该模型记为AR(p)，它的功率谱为：

(2)

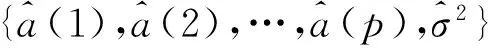
(3)

将式(1)乘以x(n-m) 求平均(数学期望)，可以求得观测数据的AR(p)模型参数与自相关函数的关系式为:

(4)

由式(4)可知自相关函数Rxx具有递推的性质，将式(4)写成矩阵形式得:

最后，大力发展科技服务中介机构。加快落实《市政府办公室关于加快科技服务业发展的实施意见》要求，重点培育市场化、专业化的人才中介、研究开发、技术转移、检验检测认证、科技金融等科技中介服务机构，加强对责任部门实施情况绩效考核。着力打造“科技领军型人才创新驱动中心”服务品牌，完善领军型人才驱动中心服务职能建设，提升政府招才引才育才工作社会影响力。

(5)

式(5)就是著名的Yule-Walker(Y-W)方程。式(5)表明，只要获取观测数据{x(0),x(1),…,x(N-1)}的自相关函数，就能估计出AR模型的参数{a(k)|k=1,2,…,p}和σ2，进而按式(3)求得信号功率谱的估值。目前AR模型参数的提取算法主要有Levinson-Durbin算法、Burg算法和Marple算法3种，本文主要研究基于Burg算法的功率谱估计。

1.2 Burg算法

Burg算法的基本思想是基于线性预测器的前、后向预测的总均方误差之和最小的准则直接从观测数据来估计反射系数，然后通过Lenvinson-Durbin算法的递推公式求出AR模型参数。这种方法的优点就是对未知数据不需要做任何假设，估计精度较高。假设观察到的N个数据为X(0),X(1),X(2)，…，X(N-1)，则具体算法如下：

(1) 初始化前、后向预测误差以及预测误差功率：

(6)

(7)

(2) 计算反射系数:

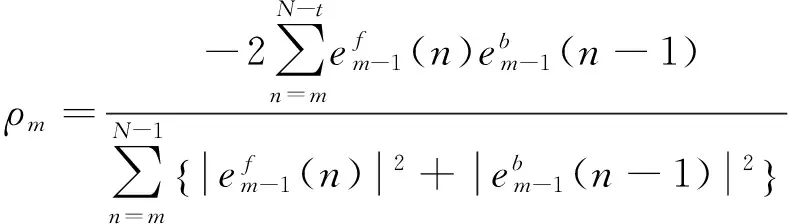
m=1,2，…，p

(8)

(3) 计算滤波器系数及预测误差功率:

am(m)=ρm

(9)

am(k)=am-1(k)+ρmam-1(m-k)，

k=1,2,…，m-1

(10)

(11)

(4) 递推高一阶前、后向预测误差:

(12)

(13)

把m更新为m+1，重复步骤(2)至步骤(4),直到预测误差功率Em满足要求。

2 Burg算法的参数选择分析

为了分析Burg算法的参数选择对功率谱估计的影响，本文首先构建仿真信号为：

x(t)=5sin(2πf1t)+3sin(2πf2t)+n(t)

(14)

2.1 采样频率的选择对功率谱估计的影响

为了分析Burg算法中采样频率的选择对功率谱估计的影响，必须保证采样点数、AR模型阶数和FFT长度恒定。现令采样点数N=512，AR模型阶数p=100，FFT长度为2 048，采样频率分别选择500 Hz,1 kHz,5 kHz和10 kHz。对信号x(t)进行功率谱估计，仿真结果如图1所示。

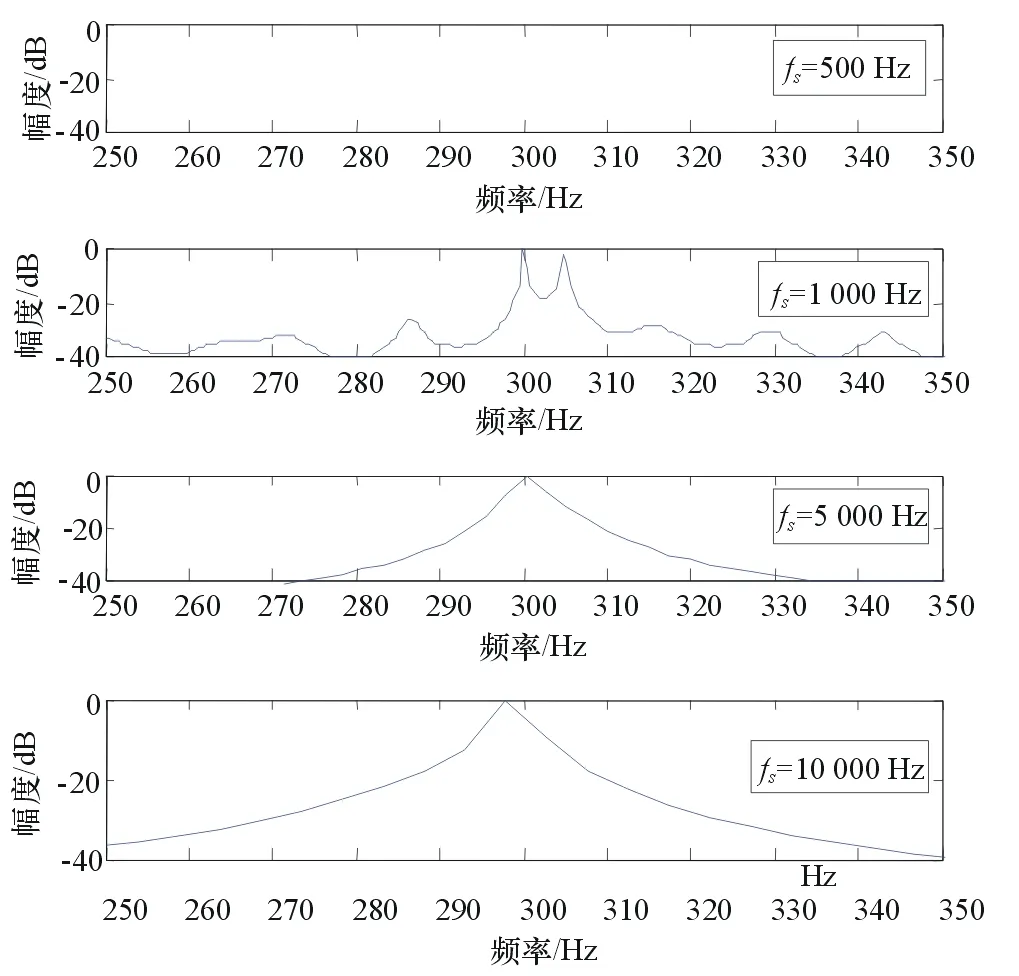
图1 采样率不同时的功率谱估计

由仿真图形可知，当采样频率过低，fs=500 Hz<710 Hz，无法满足采样定理时，不能完成功率谱估计；采样频率逐渐增大，fs=1 000 Hz时，能够清晰分辨出信号的2个谱峰；当采样频率选择过大，fs=5 kHz和10 kHz时，信号的2个频率出现频谱混叠，仅能发现一个谱峰，无法完成功率谱估计。因此，采样频率的选择必须满足采样定理，不能过小；同时也要避免采样频率选择过高导致的频谱混叠，一般选择fs∈[3fmax,4fmax]。

2.2 采样点数的选择对功率谱估计的影响

设定采样频率为1 kHz，AR模型阶数p=100，FFT长度为2 048，采样点数分别为N=128，512，2 048和8 192，仿真结果如图2所示。

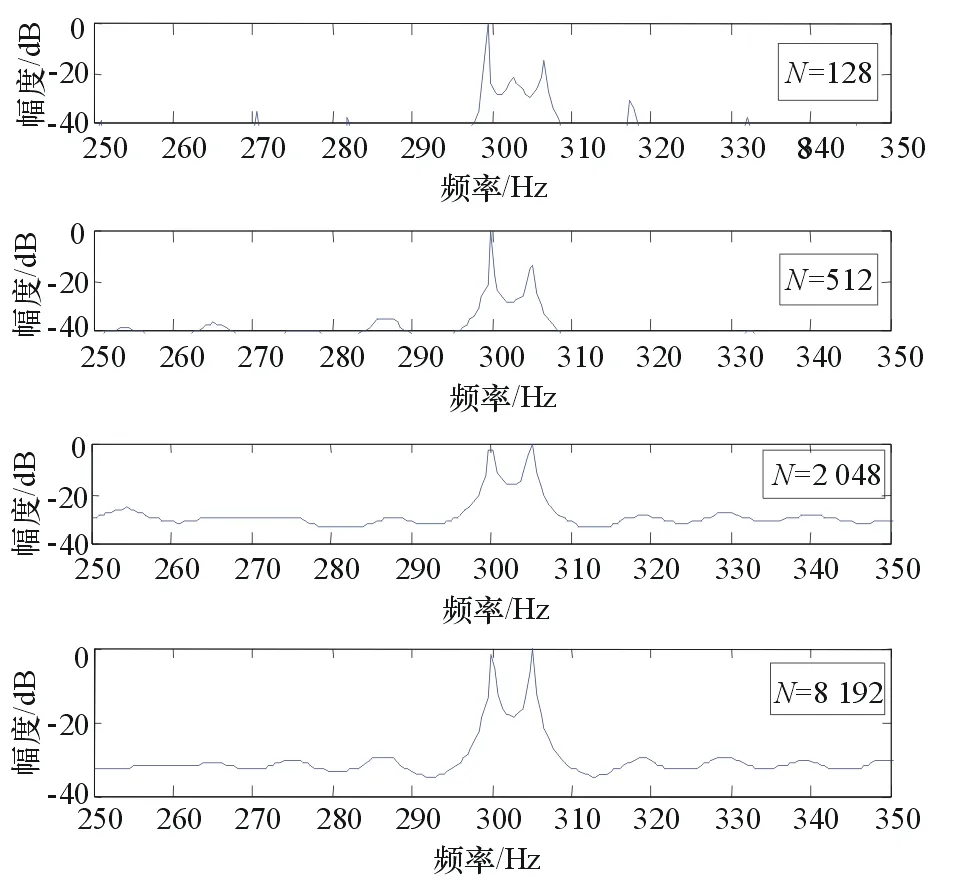
图2 采样点数不同时的功率谱估计

由图2可知，当采样点数很小，N=128时，谱估计的分辨率很低，而且出现了谱峰分裂的现象。随着采样点数的增加，获得的数据会越来越多，谱估计的分辨率也越来越高，但同时也会增大整个谱估计的运算量。对此必须综合考虑，选择合适的采样点数，在保证分辨率的同时，尽量减小运算量。

2.3 FFT长度的选择对功率谱估计的影响

设定采样频率为1 kHz，AR模型阶数p=100，采样点数为N=512。FFT长度分别为512,1 024,2 048和4 096。仿真结果如图3所示。

图3 FFT长度不同时的功率谱估计

由图3可知，随着FFT长度的增大，2个谱峰变得更清晰陡峭，功率谱估计的分辨率也更高，但同时也必将导致算法运算量的增大。对此，选择FFT长度时必须综合考虑分辨率和算法运算量，通常选择FFT长度为2 048或4 096。

2.4 AR模型阶数的选择对功率谱估计的影响

设定采样频率为1 kHz，FFT长度=2 048，采样点数为N=512，AR模型阶数p=30，100，200和400。仿真结果如图4所示。

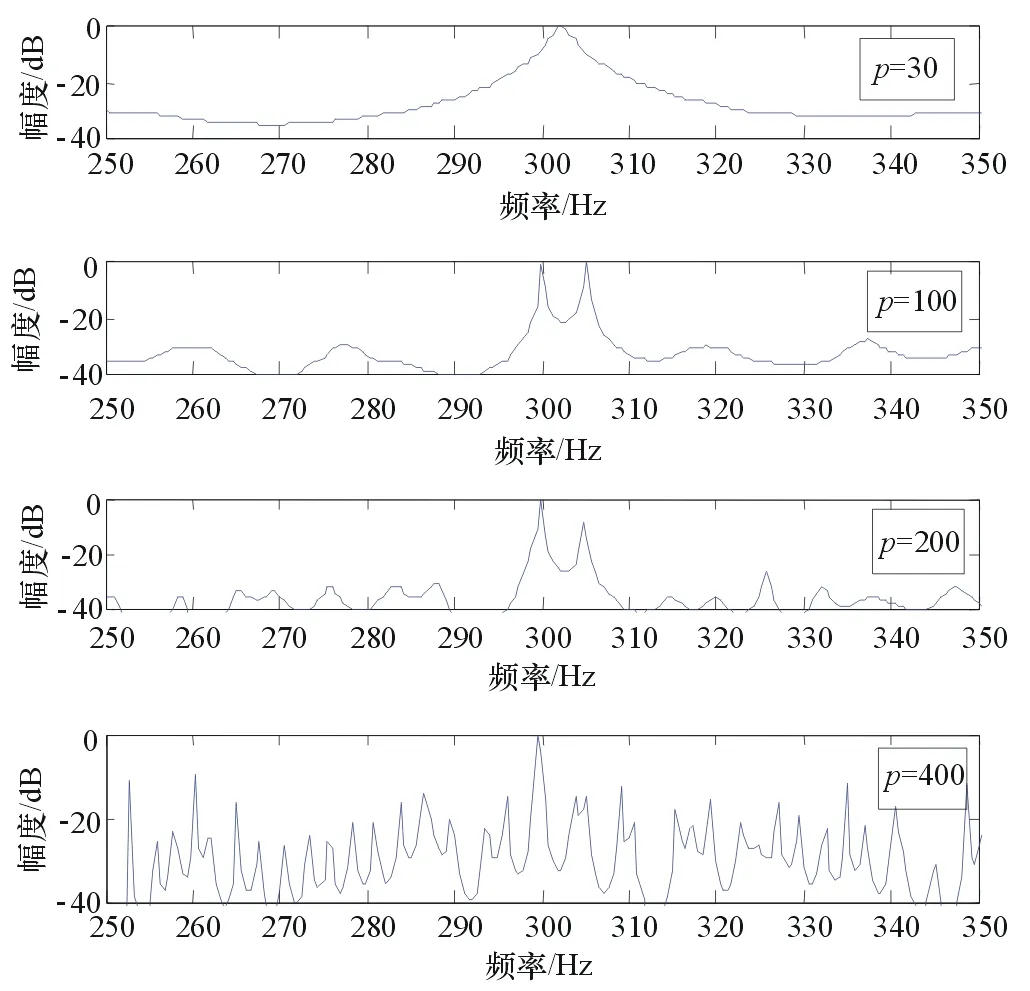
图4 AR模型阶数不同时的功率谱估计

由图4可知，当AR模型阶数较小，p=30时，分辨率很低，无法清晰分辨出2个谱峰。随着阶数的增大，分辨率逐渐增大。当p=100和200时，能够清晰分辨出2个谱峰；但当阶数过大，p=400时，2个谱峰处出现了明显的谱峰分裂，整个谱估计出现了大量的虚假峰，无法正确估计出频率所在位置。因此，在选择AR模型阶数时，必须在保证分辨率的同时避免谱峰分裂情况的出现。综合比较，本文选择p=100较为合适。

3 实验数据验证

列车测速系统采用多普勒雷达体制，工作原理基于多普勒效应。测速天线置于列车车厢下方，以角度θ向地面发射雷达波。当列车以速度v(t)运动时，根据多普勒效应，接收到的雷达波会产生多普勒频移fd，如图5所示。多普勒频移fd与列车运行速度v(t)的关系如下：

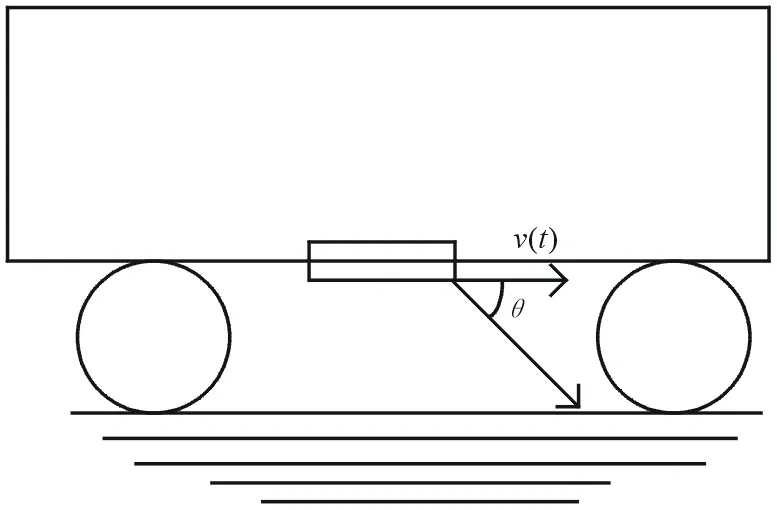
图5 列车测速原理图

(15)

式中：λ为雷达信号波长；θ为波束主瓣方向与列车行驶方向的夹角；v(t)为列车相对地面的行驶速度。

为了更好地探测列车速度，避免因颠簸震动导致的雷达天线与地面夹角的变化，本文采用的列车测速系统使用角度补偿的方法，向地面发射2个存在固定夹角的雷达波束，保证了多普勒雷达列车测速系统的稳定性。

为了验证第2节中Burg算法参数选择分析正确与否，本文采用多普勒雷达列车测速系统进行仿真实验。其中雷达天线分别以与地面成40°和50°的方向向地面发射雷达波，2个雷达波束的夹角固定为10°，测速雷达的工作频率为f0=24.125GHz。

列车测速系统分别采集了列车速度为10～80km/h的数据，其对应的多普勒频移范围约为0.45～3.6GHz。由上节分析可知，选取采样率fs=4fmax，取整后fs=15 GHz；选取采样点数N=512；选取FFT长度为2 048；AR模型阶数选为p=100。对雷达天线与地面成40°角、列车速度为40km/h的数据进行仿真，实验结果如图6、图7所示。由多普勒频率公式可求出：

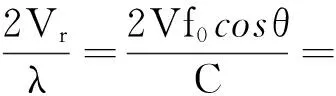
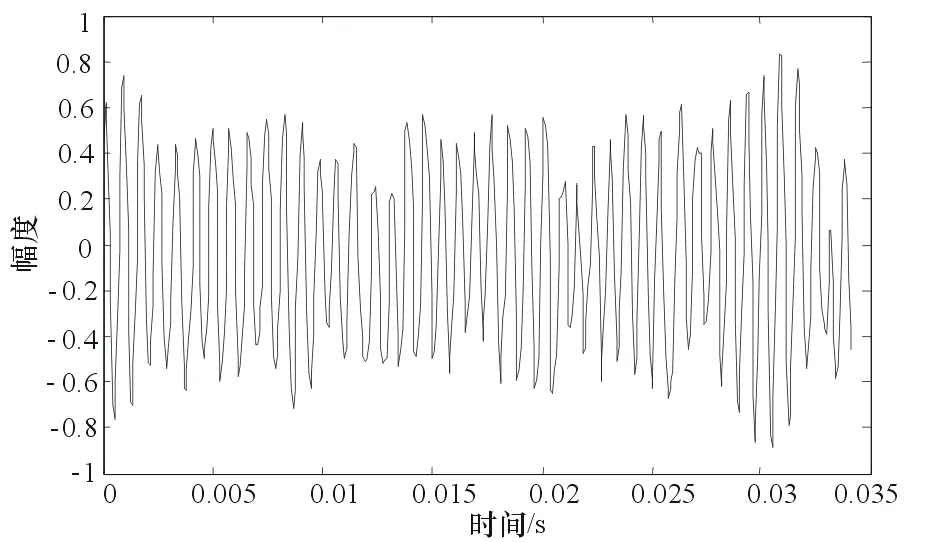
图6 列车速度为40 km/h时数据时域图

图7 列车速度为40 km/h时功率谱估计

对比图6可知，按照本文第2节中分析结果选择Burg算法仿真参数，成功地完成了对列车测速数据的功率谱估计，并且估计结果较为准确。

4 结束语

本文首先通过MATLAB仿真信号分析了采样频率、采样点数、AR模型阶数和FFT长度等Burg算法参数对功率谱估计的影响。由分析可知，采样频率的选择必须满足采样定理，同时也要避免采样频率选择过高导致的频谱混叠，一般选择fs∈[3fmax,4fmax]；选择合适的采样点数，在保证分辨率的同时，尽量减小运算量；选择FFT长度时必须综合考虑分辨率和算法运算量；在选择AR模型阶数时，必须在保证分辨率的同时避免谱峰分裂情况的出现。

为了验证分析结果，本文采用多普勒雷达列车测速系统进行仿真实验。实验结果表明，按照本文分析选择Burg算法仿真参数，能够成功地完成对列车测速数据的功率谱估计，并得到良好的功率谱估计效果。

[1] 王凤瑛,张丽丽.功率谱估计及其MATLAB仿真[J].仿真技术,2006,22(11):287-289.

[2] 罗丰,段沛沛,吴顺君.基于Burg算法的短序列谱估计研究[J].西安电子科技大学学报(自然科学版),2005,32(5):724-728.

[3] 段沛沛,罗丰,吴顺君.一种有效的短序列功率谱估计算法及其应用[J].雷达科学与技术,2004,2(6):272- 275.

[4] 蔡方凯.已调波功率谱分析研究[D].成都:电子科技大学,2005.

[5] 沈慧芳,吕容川,蔡立娜,等.基于修正Levinson算法的地杂波仿真及其应用[J].火控雷达技术,2007,36(2):17-19.

[6] 姚文俊.自相关法和Burg法在AR模型功率谱估计中的仿真研究[J].计算机与数字工程,2006,35(10):32- 34.

[7] 田坦,李延.伯格谱估计算法的一种改进[J].数据采集与处理,2002,17(3):276-278.

[8]MARPLESL.Anewautoregressivespectrumanalysisalgorithm[J].IEEETransactionsonAcoustics,Speech,andSignalProcession,1980,28(4):441-454.

ParametersSelectionofPowerSpectrumEstimationBasedonBurgAlgorithm

HUANGChao,WANGWei,SHANLiang

(ElectronicEngineeringInstitute,Hefei230037,China)

ThispaperintroducesBurgalgorithmbasedonautoregressive(AR)modelinmodernpowerspectrumestimation,analyzestheinfluenceofparameterselectioninBurgalgorithmonpowerspectrumestimation,andgivesthecomprehensiveoptimalparameterselectionmethodbasedonBurgalgorithm,finallyappliestheparameterselectionmethodproposedinthispapertotrainspeeddetectionsystemforexperimentvalidation,estimatestheDopplerfrequencyoftrainaccurately.

powerspectrumestimation;autoregressivemodel;Burgalgorithm;parameterselection

2015-08-31

TN

A

CN32-1413(2016)05-0085-05

10.16426/j.cnki.jcdzdk.2016.05.022