基于PSO的直线电机式混合悬架参数优化
2016-12-12吴麟麟施明敏汪若尘丁仁凯
吴麟麟,施明敏,汪若尘,丁仁凯
(江苏大学 汽车与交通工程学院,江苏 镇江 212013)
基于PSO的直线电机式混合悬架参数优化
吴麟麟,施明敏,汪若尘,丁仁凯
(江苏大学 汽车与交通工程学院,江苏 镇江 212013)
提出了一种直线电机与减振器并联的混合悬架,用于实现悬架振动能量回收。针对混合悬架动力学性能和馈能性能之间矛盾关系,首先建立混合悬架动力学模型,研究了减振器阻尼系数对混合悬架性能影响,并将阻尼系数作为优化设计变量,以混合悬架的舒适性、安全性和馈能特性为优化目标,建立多目标优化函数,以1/4车辆模型为研究对象,采用多目标粒子群算法求全局最优解。优化之后提升了混合悬架馈能性能,且兼顾悬架动力学性能,表明该算法在混合悬架参数优化方面具有较好效果。最后进行了1/4台架试验,验证了优化结果的有效性,为节能型悬架的研究提供参考。
混合悬架;馈能;粒子群算法;直线电机
悬架系统是车辆底盘关键总成之一,它是车架(或车身)与车轴(或车轮)弹性连接机构的总称[1-3]。传统被动悬架通过阻尼器衰减路面冲击,并以热能的形式将振动能量耗散到空气中。但确定的结构参数无法兼顾车辆不同动力学性能(乘坐舒适性和行驶安全性)要求[4]。主动悬架突破了被动悬架的局限性,极大地改善了车辆的隔振性,但在抑制振动过程中需额外消耗大量的外部能源[5-7],增加了动力源(发动机/电动机)的功率输出,因此限制了其在车辆上的应用。
近年来,随着电控技术的发展,各国学者开始研究振动能量回收。将回馈的能量(电能)用于驱动自身工作或用于车辆上的其他电气设备[8-9],从而降低整车能耗。
Smith设计了车辆振动能量回收系统,研究了振动能量回收的效率,通过试验证明了振动能量回收具有可行性;Suda[10-11]试制了直流旋转电机结合滚珠丝杠机构的电磁阻尼器,并引入行星齿轮机构,将其应用到载重卡车驾驶室上,通过回收的能量驱动电机,抑制驾驶室的振动;Nakano[12]提出利用一个直线直流电机作动器来实现悬架系统的主动控制和振动能量。
本文选用直线电机作为电磁作动器,与弹簧和减振器并联组成混合悬架,对振动能量进行回收。混合悬架具有2种工作模式,即随动馈能模式和主动减振模式,在随动馈能模式下,作为发电机回收悬架振动能量,在主动减振模式下,作为电动机保证悬架的减振性能。本文研究了在随动馈能模式下,针对混合悬架在回收能量过程中馈能特性和动力学性能间存在矛盾冲突关系,采用粒子群算法对减振器器阻尼系数Cs进行参数优化[13-15],使混合悬架在兼顾动力学性能前提下,提高馈能性。
1 混合悬架建模及参数分析
1.1 混合悬架建模
图1建立了混合悬架理想线性二自由度模型,将滤波白噪声作为路面输入。图中:ms为车身簧载质量 ;mu为簧下质量;ks为悬架弹簧刚度;cs为悬架减振器阻尼系数;Fm为直线电机等效阻尼力;zr为路面位移起伏;zu为簧下质量垂向位移;zs为簧载质量垂向位移。
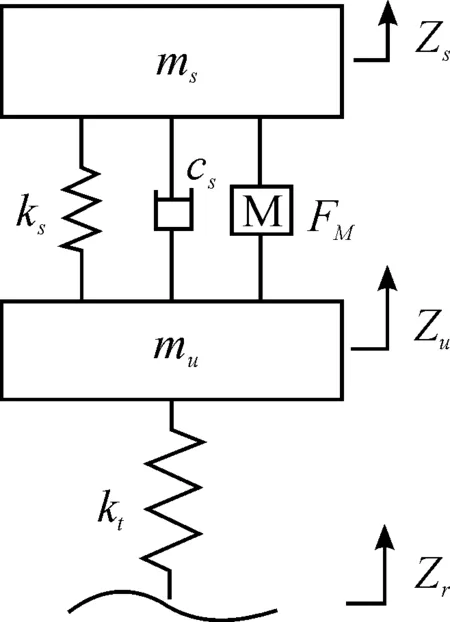
图1 理想线性二自由度悬架模型
(1)
路面输入可表示为:
(2)
当直线电机回收能量时,永磁体与线圈产生相对运动,根据法拉第电磁感应定律,线圈将产生感应电动势,从而将振动能量转换为电能。同时,电机将产成电磁阻尼力,该电磁阻尼力始终阻碍永磁体与线圈的相对运动。此时,直线电机相当于被动阻尼器,其等效阻尼及阻尼力可表示为:
ceq=keki/Rm
(3)
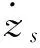
(4)
其中:ke为电机反电势系数;ki为电机推力系数;Rm为电机内阻。混合悬架系统参数如表1所示,直线电机参数如表2所示。
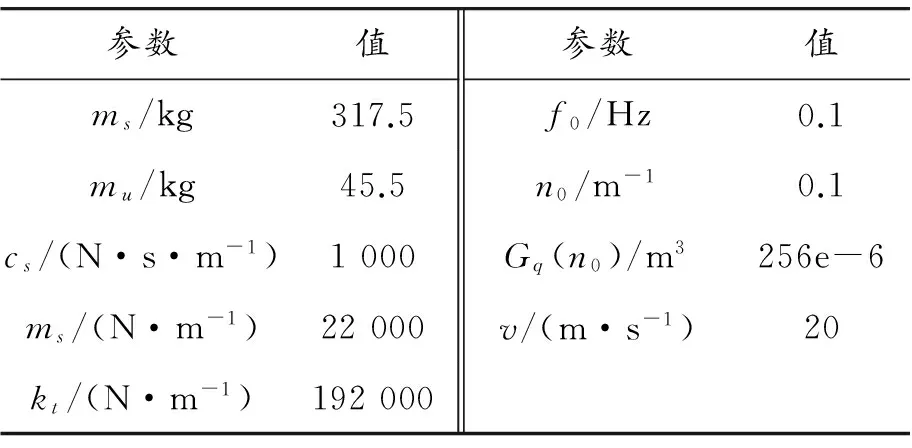
表1 悬架系统参数

表2 直线电机参数
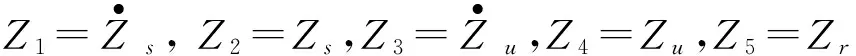
Z=[Z1Z2Z3Z4Z5]为系统控制变量,则系统状态方程可表示为

(5)
其中,A,B,F,C,D为系统状态方程,可由式(1)得到。
1.2 混合悬架参数分析
在传统被动悬架系统中,弹簧起支撑车身重量作用,阻尼减震器将部分振动能量以热能形式耗散掉,从而抑制车身振动。而混合悬架在回收能量时,直线电机等效于阻尼器,加入直线电机,改变系统阻尼值,此时系统阻尼为
C=Cs+Ceq
(6)

由上述可知,混合悬架减振器阻尼系数Cs与馈能效率存在负相关的关系,即增大Cs将降低馈能效率。同时,Cs变化也会影响悬架动力学性能。因此,本文把Cs作为悬架系统优化参数。
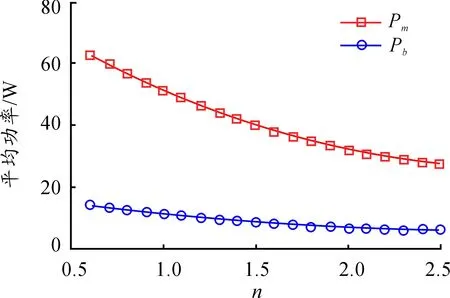
图2 n对馈能效率影响
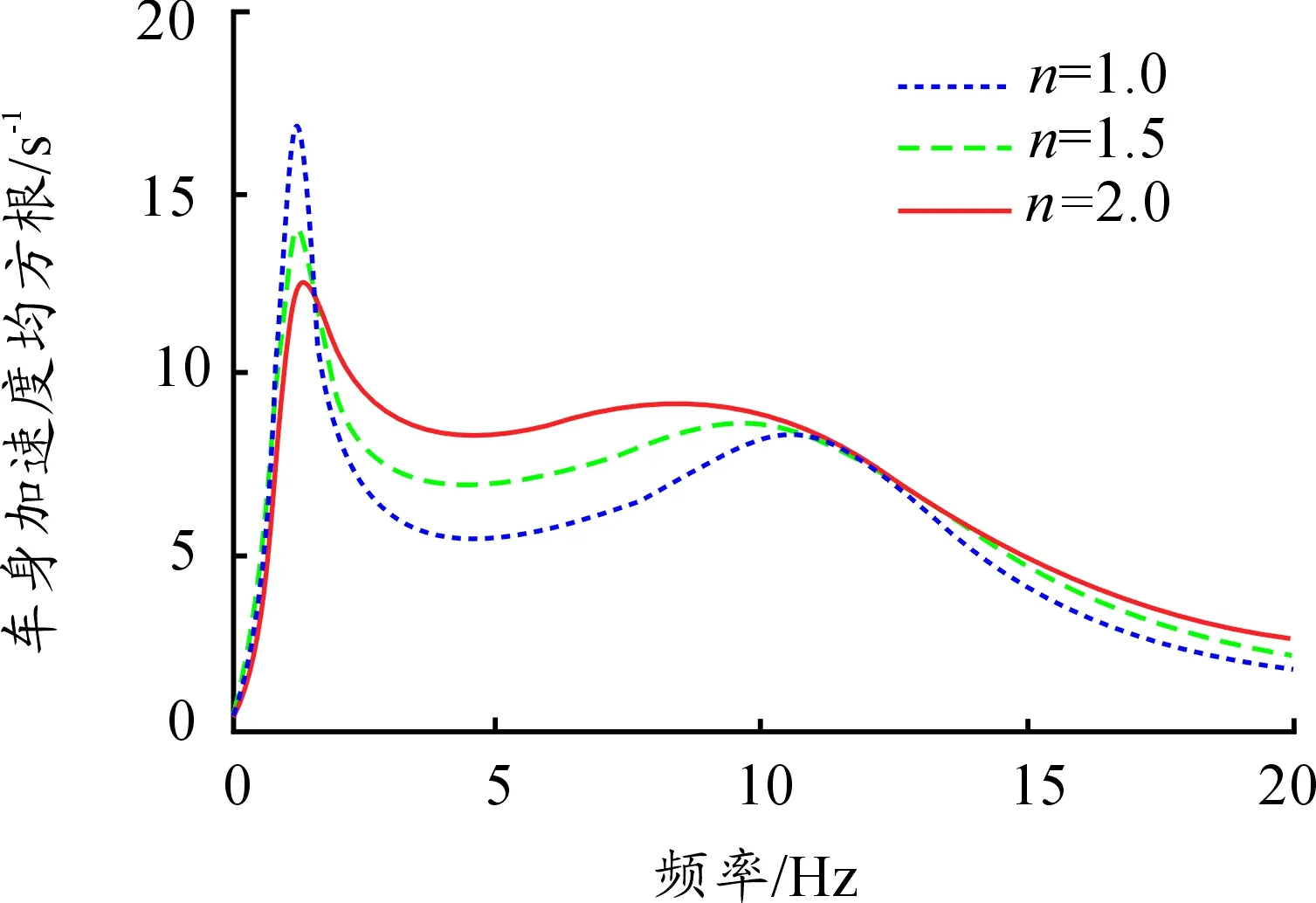
图3 n对动力学性能影响
2 混合悬架参数优化
混合悬架系统的主要性能指标有代表乘坐舒适性的车身加速度、代表车辆安全性的轮胎动载荷以及代表悬架馈能性的减振器阻尼系数与直线电机等效阻尼值之比,以车身加速度、轮胎动载荷和减振器阻尼系数与直线电机等效阻尼值之比。为优化目标,建立需要优化的适应度函数。
2.1 目标函数的建立
目标函数为:
F(x)=λ1f1(x)+λ2f2(x)+λ3f3(x)
(7)
式中:λ1为舒适性加权因子;λ2为安全性加权因子;λ3为馈能性加权因子;f1(x)为舒适性分目标函数;f2(x)为安全性分目标函数;f3(x)为馈能性分目标函数。f1(x)为车身加速度均方根值。f2(x)为轮胎动载荷均方根值。f3(x)为减振器阻尼系数与直线电机等效阻尼值之比。
2.2 约束条件
1) 当混合悬架固有频率与人体所习惯步行时身体上下运动的频率相一致时,即1~1.5 Hz,人体感觉较舒适,此时即可保证车辆行驶过程中的舒适性能(f为混合悬架固有频率),即
(8)
2) 根据汽车理论等相关文献介绍,汽车悬架的阻尼属于小阻尼,一般汽车悬架系统的阻尼比范围是0.2≤ξ≤0.4,即
(9)
3) 车轮与路面间的相对动载荷,对汽车行驶安全性、路面的破坏有很大的影响,当轮胎动载荷均方根值σFd不超过静载荷的1/3时,车轮跳离地面的概率小于0.15%,此时即可保证混合悬架安全性,即
(10)
2.3 参数优化
传统悬架参数优化多采取遗传算法(GA),但遗传算法往往局部搜索能力较弱,且需要通过二进制进行编码解码,实现较为复杂。而粒子群算法通过搜索空间中的追随最优粒子,无需过多调整参数及交叉变异,使得算法更加容易实现,同时具有较强的优化能力。
在PSO算法中,每个粒子即代表所求问题的个潜在解,粒子在搜索空间中以一定的速度进行搜索,并通过对个体和集体搜索经验的学习,动态更新粒子自身的位置和速度在m维搜索空间中,粒子在t时刻的位置和速度用向量xt=(xt1,xt2,…,xtm),vt=(vt1,vt2,…,vtm)表示,更新公式为:
(11)
式中:ω为惯性权重;r1,r2为加速因子;g1,g2为[0,1]之间随机数;pt为粒子在t时刻的自身最好位置pbest;Gt为粒子全局最好位置,即所有粒子中的最好位置Gbest。
根据本文实际的优化要求,具体的算法流程如下:
1) 初始化参数,包括种群规模、惯性权重ω、粒子维数m、最大迭代次数Dmax、 粒子加速因子r1和r2等;
2) 根据设定参数范围,随机产生所有粒子的位置及粒子初始速度;
3) 将每个粒子的位置赋值为混合悬架参数,根据混合悬架仿真结果计算车身加速度均方根值、轮胎动载荷均方根值以及减振器阻尼系数与直线电机等效阻尼值之比;
4) 定义车身加速度均方根值为粒子适应度函数,同时对约束条件进行判定,若不符合车辆舒适性要求,即混合悬架固有频率f>1.5 Hz或f<1 Hz,粒子将停止适应度计算,直接进行更新;
5) 计算符合约束要求的粒子适应度,确定粒子的pbest和Gbest;
6) 根据粒子间位置关系,利用式(11)更新粒子速度;
7) 更新每个粒子的个体极值和粒子群全局极值;
8) 若迭代次数增加未满足结束条件,转步骤 5),否则取gbest为最优解。
2.4 优化结果分析
利用Matlab编写粒子群算法程序,经过多次优化结果对比,设置相关参数如下:种群规模50,粒子维度6,最大迭代次数100。初始惯性权重ω=0.73, 加速因子r1=r2=1.36,适应度要求设定为0.1。减振器阻尼值优化结果为828 N·s·m-1,如图4所示。

图4 优化结果
为了验证优化所得的减振器器阻尼值对于混合悬架馈能性和动力学性能的影响,对优化前后的混合悬架主要性能指标进行仿真对比。同时,假定车辆以20 m/s的速度在C级路面上行驶。得到部分仿真结果如表3和图5~8所示。

表3 仿真数据
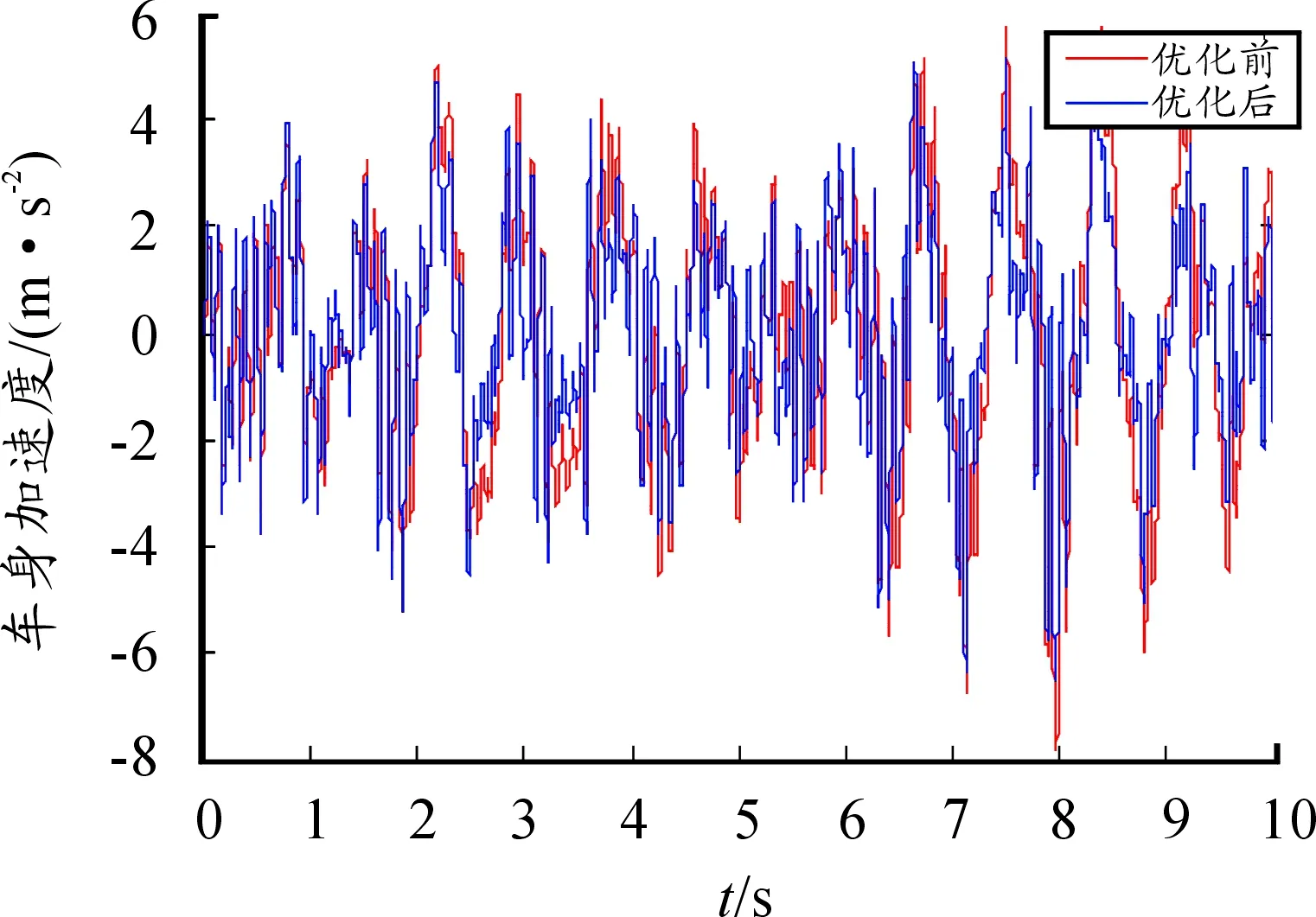
图5 车身加速度
由表3可知:优化后的加速度均方根值降低了5.29%,表明车辆乘坐舒适性得到一定幅度的提高,而优化之后轮胎动载荷均方根值增加了12%,表明车辆的行驶安全性略有下降。同时,超级电容端电压由13.9 V增加到14.8 V,提升了6.47%,表明优化之后混合悬架的馈能性得到一定提高。
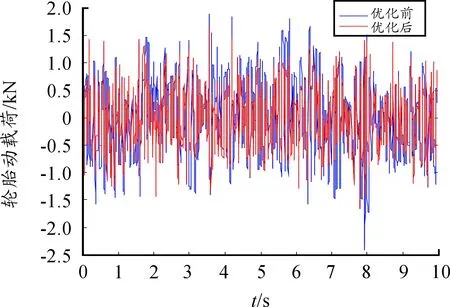
图6 轮胎动载荷

图7 直线电机瞬时功率

图8 超级电容端电压
3 台架试验
为了验证优化仿真结果的正确性,进行了1/4台架试验。试验结构布置如图9所示。直线电机的动子和可调减振器的缸筒与轮胎相连,动子和可调减振器活塞杆与簧上质量相连。试验参数与仿真参数一致,激振台可模拟随机路面输入。加速度传感器分别用于测量簧上质量与簧下质量加速度,簧上质量与簧下质量的速度可由测量的加速度积分得到。路面输入可用INSTRON 8800数控液压伺服激振试验台模拟。

图9 台架试验结构布置
试验结果如图10~12所示。由于仿真是理想线性状态,而试验中存在诸多非线性因素,图中出现部分偏差属于正常范围。而超级电容电压图中,试验与仿真升压趋势保持一致,验证了优化结果的有效性。

图10 车身加速度

图11 轮胎动载荷

图12 超级电容端电压
4 结束语
本文提出了一种在传统被动悬架基础上并联直线电机的混合悬架结构。该悬架结构可回收振动能量。直线电机的加入改变了悬架的系统阻尼大小,同时影响悬架动力学性能。由于当前混合悬架回收能量有限,需在兼顾悬架动力学性能基础上提高其馈能性能。因此,采用粒子群算法对减振器阻尼值进行优化。结果表明:优化之后回收振动能量的超级电容端电压提升了6.47%,表明悬架的馈能性得到提高,同时保证了悬架动力学性能。最后进行了1/4台架试验,试验结果与仿真基本一致,验证了优化结果有效性。该研究成果对于今后节能型悬架的开发具有一定的参考意义。
[1] 唐诗晨,陈龙,汪若尘,等.基于阻尼多模式切换的主动悬架最优控制研究[J].广西大学学报(自然科学版),2014,39(2):300-307.
[2] 李仲兴,晋旋,江洪.基于NSGA-Ⅱ悬架参数优化设计[J].拖拉机与农用运输车,2010,37(1):29-31.
[3] 江洪,李坤,周文涛,等.ECAS系统控制模式及控制策略[J].机械工程学报,2009,45(12):224-231.
[4] MONTAZERI-GH M,KAVIANIPOUR O.Investigation ofthe active electromagnetic suspension system considering hybrid control strategy.Proc IMechEPart C[J].J Mechanical Engineering Science,2014,228(10):1658-1669.
[5] 曹民,刘为,喻凡.车辆主动悬架用电机作动器的研制[J].机械工程学报,2008,44(11):224-228.
[6] 喻凡,曹民,郑学春.能量回馈式车辆主动悬架的可行性研究[J].振动与冲击,2005,24(4):27-30.
[7] 陈双,宗长富,刘立国.主动悬架车辆平顺性和操纵稳定性协调控制的联合仿真[J].汽车工程,2012,34(9):791-797.
[8] 陈星,罗虹,邓兆祥.直线电机馈能悬架控制系统设计与馈能分析[J].振动与冲击,2012,31(8):124-129.
[9] 于长淼,王伟华,王庆年.混合动力车辆馈能式悬架的节能潜力[J].吉林大学学报(工学版),2009,39(4):841-845.
[10]SUDA Y,SHIIBA T,HIO K,et al.Study on electromagnetic damper for automobiles with nonlinear damping force characteristics (road test and theoreticalanalysis)[J].Vehicle System Dynamics,2004,41:637-646.
[11]NAKANO K,SUDA Y.Combined type self-powered active vibration control of truck cabins[J].Vehicle System Dynamics,2004,41:449-473.
[12]NAKANO K,SUDA Y,NAKADAI S.Self-powered active vibration control using a single electric actuator[J].J Sound and Vibration,2003,260:213-235.
[13]孙晓强,陈龙,汪少华,等.2级串联式ISD悬架非线性建模与参数优化[J].农业机械学报,2014,45(6):7-13.
[14]张武,陈建,高煜.基于粒子群优化的发动机悬置系统稳健优化设计[J].农业机械学报,2010,41(5):30-35.
[15]刘顺安,胡庆玉,高春甫,等.IPSO-BP算法在半主动悬架控制中的应用[J].北京工业大学学报,2011,37(9):1281-1286.
(责任编辑 刘 舸)
Parameter Optimization of Hybrid Suspension with Linear Motor Based on PSO
WU Lin-lin, SHI Ming-min, WANG Ruo-chen, DING Ren-kai
(School of Automobile and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)
A kind of mixed suspension is proposed in this paper to recovery suspension vibration energy. It consists of linear motor and damper in parallel. In order to coordinate the dynamic performance and energy recovery performance of suspension, firstly,the dynamic model of mixed suspension was established. The damper’s impact on mixed suspension was studied, and the damper-coefficient was set as optimization parameters.Then the comfort,safety and energy recovery performance of mixed suspension was set as optimization goal.Multi-objective optimization function was set.And 1/4 suspension model was set as the object of study. Multi-objective particle swarm optimization (PSO) was used to seek global optimal solutions. The energy recovery performance was promoted, and the dynamic performance was considered after optimization. It indicated that the algorithm has better effect in the mixed suspension parameters optimization. Finally, 1/4 bench test was carried out, and it demonstrated the effectiveness of the optimization results. The studycan provide reference for the research of energy-saving suspension.
hybrid suspension; energy regeneration; particle swarm optimization; linear motor
2016-07-18 基金项目:江苏省高校自然科学研究重大项目(15KJA460005)
吴麟麟(1970—),男,江苏泰兴人,博士,副教授,主要从事汽车理论研究,E-mail:wangjust@ujs.edu.cn。
吴麟麟,施明敏,汪若尘,等.基于PSO的直线电机式混合悬架参数优化[J].重庆理工大学学报(自然科学),2016(11):12-17.
format:WU Lin-lin,SHI Ming-min,WANG Ruo-chen,et al.Parameter Optimization of Hybrid Suspension with Linear Motor Based on PSO[J].Journal of Chongqing University of Technology(Natural Science),2016(11):12-17.
10.3969/j.issn.1674-8425(z).2016.11.003
U463.1
A
1674-8425(2016)11-0012-06
