基于模型的车辆质心侧偏角估计方法研究
2016-12-12柳惠
柳 惠
(江苏大学 汽车与交通工程学院,江苏 镇江 212013)
基于模型的车辆质心侧偏角估计方法研究
柳 惠
(江苏大学 汽车与交通工程学院,江苏 镇江 212013)
为实现对车辆操纵稳定性控制,建立了车辆单轨2自由度数学模型对车辆的质心侧偏角进行估算。以扩张观测理论为基础,设计了一种能够实时追踪状态变量的质心侧偏角观测器,利用可以直接获取的横摆角速度、车轮转角和纵向车速对质心侧偏角进行估计。在Matlab中对设计的质心侧偏角观测器进行仿真,并利用BOSCH的实验室进行实验验证。
车辆行驶状态估计;观测器;实时追踪;稳定性控制
随着汽车数量的增加,交通状况变得越来越复杂,对车辆稳定性的要求也越来越高。汽车厂商开发了ABS及ESP等车辆稳定性电子控制系统,通过主动干预汽车的制动力及其大小和分布来改善车辆的操纵稳定性。
汽车稳定性控制需要根据获取的车辆行驶状态参数来判断是否对车辆进行主动干预,其中横摆角速度和质心侧偏角是重要的2个参数。横摆角速度可以通过传感器直接获取,而质心侧偏角难以直接获得,或获取的成本比较高。如何通过可以直接或间接测量的车辆行驶参数对车辆质心侧偏角进行准确估计成为车辆稳定性控制研究必须解决的重要问题。
目前大部分质心侧偏角估计算法都依赖于模型的准确性,且容易受到干扰,对参数估计的实时性和准确性造成一定的影响。本文基于扩张观测理论设计了一种变结构抗干扰的质心侧偏角观测器,计算简单,容易实现,能对质心侧偏角进行准确的估计。
1 扩张观测理论
n阶非线性系统:
,….,X(n-1),t)+bu(t)
(1)
式中:f(·)为未知函数;u(t)为已知的系统输入;X(t)为测量输出。可根据式(1)构造出不依赖于f(·)的系统,使它能由可测量的x(t)估计出被扩展的状态变量x(n),则改写式(1)为如下非线性系统:
(2)
选取适当的非线性函数gi(z)可以让系统(2)的各状态变量跟踪系统(1)的状态变量:
即:
系统(1)则等价于:
(3)
其中b(t)为未知函数。若记δx1=z1-x1(t),δx2=z21-x2(t),δxn-1=zn-1-xn-1(t), 则系统(3)可变为:
(4)
选择合适的函数g使得系统(2)能跟踪系统(1)。
这种变结构观测器与原系统表达式无关,仅与实时值变化b(t)范围有关,故这种观测器具有一定范围内的适应性和鲁棒性,优于一般观测器。
若令gi(z)=βig(z),g(z)为非线性函数,则构造的状态观测器可以表示为:
(5)
选取适当的系数和非线性函数g()就可以让系统(5)的状态变量分别跟踪系统(1)的各状态变量。
2 车辆质心侧偏角估计模型
汽车主动安全控制系统中主要以横摆角速度和质心侧偏角作为控制变量,因此本文建立包含横摆于侧向运动的2自由度车辆模型,如图1所示。
该模型的状态方程为:
(6)
式中:a,b为质心到前后轴的距离;k1,k2为前后轮胎侧偏刚度;m为整车质量;Vx为纵向车速;δ为前轮转角;β为质心侧偏角;ω为横摆角速度;Ι为车辆转动惯量;ay为侧向加速度。

图1 2自由度车辆模型
3 车辆质心侧偏角观测器设计
由扩张观测理论可得:
(7)
将式(7)进行如下扩展:
(8)
则车辆质心侧偏角观测器设计为:
(9)
选择合适的非线性函数g()和相关参数,系统(9)的状态变量z1,z2可以很好地追踪系统(7)的状态变量x1,x2,则由式(7)第2个方程得
(10)
非线性函数g()为
(11)
状态观测器参数见表1。

表1 状态观测器参数
在Matlab软件中建立此质心侧偏角观测器的模型,如图2所示。

图2 质心侧偏角观测器Matlab模型
4 实验分析
在BOSCH的Labcar实验台(如图3所示)上对所建立的质心侧偏角估计观测器进行验证。通过计算机软件与Labcar进行通讯可以模拟车辆各种行驶状态和驾驶环境。

图3 车辆试验台
实验结果见图4。图4为选取蛇形实验工况对设计的质心侧偏角估计方法进行验证。由图4(b)可以看出:系统的状态变量x1实时跟踪效果良好。由图4(c)可见:设计的质心侧偏角变结构观测器对车辆的质心侧偏角具有良好的实时估计效果。实验验证时,改变系统的参数发现跟踪效果不受影响,说明变结构质心侧偏角观测器具有较强的自抗干扰能力。
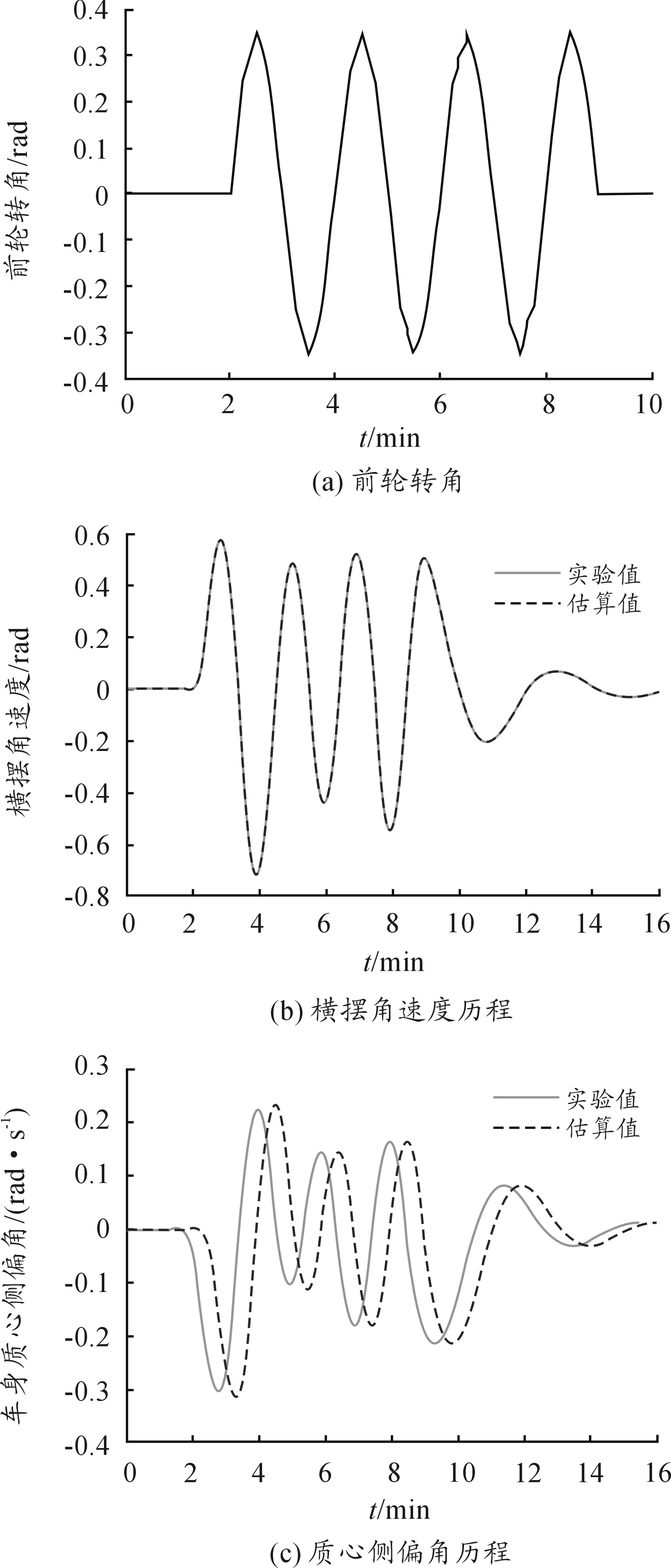
图4 实验结果
5 结束语
以扩张观测理论为基础,设计了汽车质心侧偏角的估计算法。该算法对原有的系统的状态变量进行扩展,不依赖于系统具体模型,具有良好的自抗干扰能力。该算法通过求解普通方程得到车辆质心侧偏角,计算简单,实时性好。在Labcar试验台和Matlab上对该算法进行验证,结果表明:本文设计的变结构质心侧偏角观测器结果准确,抗干扰能力强,跟踪能力强,为ESP的控制做了充足的准备。
[1] DEEPAK K K,JAYWANT P S E T.Extended state observer based robust control of wing rock motion[J].Elsevier Journal,2014.
[2] GUO Baozhu,ZHAO Zhiliang.On the convergence of an extended state observe for nonlinear systems with uncertaintr[J].Systems & Control Letters,2011(6):1890-1896.
[3] 余卓平,高小杰.车辆行驶状态中的状态估计问题综述[J].机械工程学报,2009,45(5):20-33.
[4] 韩京清.自抗扰控制器及其应用[J].控制与决策,1998,13(1):19-23.
[5] 庄继德.汽车电子控制系统工程[M].北京:北京理工大学出版社,1998.
[6] 余志生.汽车理论[M].5版.北京:机械工业出版社,2009.
[7] HUANG Yi,HAN Jingqing.Analysis and design for the second order nonlinear continuous extended states observer[J].Chinese science Bulletin,2000,45(21):1938-1944.
[8] BOUTAT D.Extended nonlinear observer normal forms for a class of nonlinear dynamical systems[J].Int J Robust Nonlinear Control,2015,25(3):461-474.
(责任编辑 刘 舸)
Side-Slip Angle of the Center of Mass of Automobile Estimation Research Based on the Model
LIU Hui
(School of Automobile and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)
In order to implement the stability control of the vehicle, the two degrees of freedom of monorail model of vehicle is established to estimate side-slip angle of the center of mass of the vehicle.A real time observer which side-slip angle of the center of mass is estimated by obtaining the angular velocity of yaw and wheel speed and wheel angel directly of side-slip angle of the center of mass is designed based on the theory of expansion of observation in this paper.The observer of side-slip angle of the center of mass of the vehicle is simulated in Matlab and validated in the ESW laboratory of BOSCH.
estimation of vehicle running state; observer; real-time tracing; control of stability
2015-12-26 基金项目:国家自然科学基金资助项目(51575001)
柳惠(1991—),男,江苏如皋人,硕士研究生,主要从事电动汽车设计与匹配分析研究,E-mail:scliuhx@foxmail.com。
柳惠.基于模型的车辆质心侧偏角估计方法研究[J].重庆理工大学学报(自然科学),2016(11):25-28.
format:LIU Hui.Side-Slip Angle of the Center of Mass of Automobile Estimation Research Based on the Model[J].Journal of Chongqing University of Technology(Natural Science),2016(11):25-28.
10.3969/j.issn.1674-8425(z).2016.11.005
U463.4
A
1674-8425(2016)11-0025-04
