长周期倒计时信号控制对排队消散特性的影响

赵 巍，徐汉清

(天津市市政工程设计研究院，天津300051)

长周期倒计时信号控制对排队消散特性的影响

赵 巍，徐汉清

(天津市市政工程设计研究院，天津300051)

长周期和倒计时是中国相对于发达国家城市道路交叉口信号控制方案的两个独有特征。基于实证数据分析两类信号控制特征对车辆排队消散特性的影响。共观测天津市两处典型的长周期倒计时信号控制交叉口的7条直行车道。实证数据表明，中国城市道路交叉口长周期倒计时信号控制下的排队消散过程大致可分为3个阶段：启动阶段、稳定阶段和上升阶段。通过有序样品聚类的方法确定3个阶段的分割点。这与HCM 2010等经典理论假设的排队消散特性明显不同，因此分析传统通行能力估计算法HCM 2010的适用性，并提出简单线性法、抛物线法和两段线法3种通行能力估计方法以减少传统方法估计中的误差。通过比较发现，抛物线与两段线拟合方法对通行能力的估计较为准确，均方根误差(RMSE)均小于30 pcu·h-1。

城市交通；信号控制；排队消散特性；通行能力；有序样品聚类；长周期；倒计时

0 引言

相对于发达国家的道路交叉口信号控制方案，中国城市普遍存在两个明显的不同特征：1)大多数倒计时数字直接通过信号灯组或通过附加LED屏显示；2)信号周期设定较长，普遍为150～300 s，特别是主干路相交或流量较大的交叉口。

研究表明，长周期或倒计时信号控制对饱和流率和通行能力会造成显著影响。然而，少有针对中国城市交通背景的研究。与长周期倒计时信号控制下车辆排队消散特性相关的研究主要包括两方面：1)饱和流率和排队消散特性；2)倒计时信号对排队消散特饱和流率增加或下降情况[7-8]。性的影响。

饱和流率是道路交叉口设计和评价的重要参数。传统理论认为，绿灯启亮后排队消散流率会迅速上升达到稳定最大值，并将维持该最大值直到排队完全消散，该稳定最大值即饱和流率[1]，HCM 2010以此为基础进行了细化分析[2]。

然而近年的研究往往会发现不同于传统排队消散的过程，部分学者通过实地数据发现排队消散过程中排队末尾车辆的车头时距存在下降趋势[3]，还有研究发现排队消散过程中消散流率呈持续下降趋势且并未出现稳定值[4]。另一些研究也发现消散过程中排队末尾的消散流率下降[5-6]。其他学者通过评估非稳定排队消散特性在通行能力和延误评估以及信号配时中的误差，发现末尾车辆出现

表1 调查地点信号配时参数Tab.1 Signal tim ing parametersof the surveyed sites s

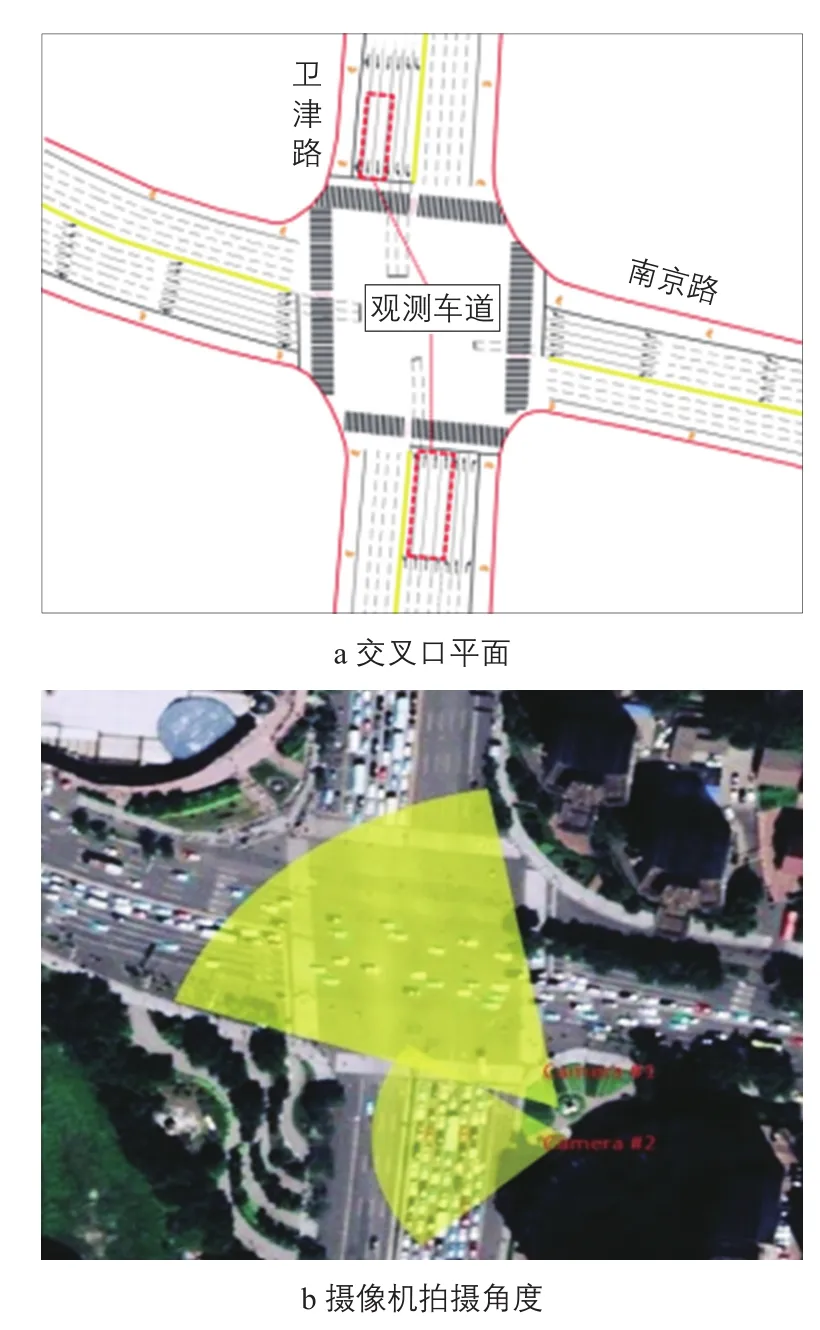
图1 研究交叉口和摄像机观测位置Fig.1 Location of targeted intersection and equipped cameras

倒计时信号对道路交叉口安全和运行效率的影响也被广泛研究，普遍采用借助有无对比或者前后对比的方法[9-10]。文献[11-12]分析了混合交通状况下倒计时信号对排队消散特性的影响，结果表明倒计时信号灯的使用使得启动损失和清空损失均明显下降，同时也发现闯红灯的倾向在绿灯末尾下降而在绿灯启动时有所升高。也有一些研究分析倒计时信号对驾驶行为和交通流参数的影响[13-14]。

基于上述讨论，本文对中国城市长周期倒计时信号控制的排队消散特性进行研究。

1 数据收集和整理

1.1 数据采集地点和数据收集

选择天津市两个典型的长周期倒计时信号控制交叉口开展调查，重点分析其中3个进口道的7个直行车道。这两个交叉口分别是卫津路—鞍山道交叉口(以下简称“AS”)和卫津路—南京路交叉口(以下简称“NJ”)。两个交叉口由主干路卫津路连接，均为主干路与主干路相交，相隔约1 km；调查对象在工作日高峰小时常处于过饱和状态，过饱和时段多为 7∶00—11∶00 和 16∶00—19∶00。在观测时段，两个交叉口均为具有左转专用相位的四相位信号控制。

AS观测南进口道2个直行车道，NJ观测北进口道3个直行车道、南进口道2个直行车道，信号配时信息如表1所示。7个观测车道宽度均大于3m，且进口道停车线附近无公共汽车站，观测车道的公共汽车很少，自行车和行人有足够的行驶空间且与机动车道采用物理隔离。

调查于2013年7月2日上午开展，采用录像法，对每个交叉口布设两台摄像机，一台记录观测车道车辆行驶情况，另一台拍摄观测车道的信号灯信息。其中NJ的几何图形和摄像机拍摄角度见图1。

1.2 数据整理

本文采集的数据重点是直行车道过饱和周期下的连续车头时距，采用方法与HCM 2010一致：以车辆后轮作为判定车辆是否驶出的参考点，将停车线作为观测断面，排队车辆包括所有的初始排队车辆和在绿灯开始后加入排队的车辆，测量精度0.02 s。为使数据更可靠，选择分析的信号周期必须满足有足够长的初始排队且交叉口小型车占主体地位。不计大型车产生的前后车头时距以排除其带来的随机干扰，保持剩余小型车驶离次序的不变。删除车辆故障等原因产生的异常车头时距。共获得146个可用周期样本和3 801个排队消散车头时距。

2 排队消散特性识别

2.1 消散特性分析

首先根据不同排队位置对应的平均车头时距变化曲线从整体上分析整个相位时长的排队消散特性(见图2)。其中“AS-SB车道一”代表鞍山道南进口的第一个直行车道，其他以此类推。可发现两个特征：

1）在第10辆排队车辆左右，消散车头时距达到2.0 s左右的相对稳定值(转换成消散流率是1 800 pcu·h-1)。这表明传统理论可能低估了启动时间的长度，传统理论认为排队车辆在第4辆车后即可达到饱和流率。

分析其原因可能为：长周期倒计时信号控制交叉口，在绿灯初期，驾驶人可通过倒计时装置了解到剩余足够的绿灯时间，以致驾驶人不愿与前车保持较小的跟车距离。而在无倒计时信号控制时驾驶人会保持更高的警惕，随时关注信号灯与前车的状态，车辆之间有较大的相互约束。

2）在排队消散的最后一部分大约从NJ第25辆车开始(AS大约从第35辆车开始)车头时距有显著下降。这与前文综述中的队尾车头时距变小的现象一致。

出现下降趋势的原因可能是：倒计时信号灯显示绿灯剩余时间，驾驶人可提前做好是否通过交叉口的心理准备，而对于长周期交叉口为了避免等待较长的红灯时间，队尾车辆趋向于通过交叉口而选择更小的车头时距。

图3为3个进口道每10 s连续绿灯间隔的平均消散流率，其中最后一个间隔代表相位的转换阶段，即3 s绿闪+3 s黄灯+1 s全红，故AS的最后时间间隔是79～＜86 s，而NJ是58～65 s。

进口道的消散流率大致可以分为3个阶段(见图4)：1)启动阶段，即绿灯启亮后消散流率快速增加的阶段，大约是前四个10 s间隔(即 0～＜10 s、10～＜20 s、20～＜30 s和30～＜40 s)；2)稳定阶段，即消散流率处在较高稳定值的阶段，这一阶段大约从30～＜40 s开始直到绿闪启亮(该时段包含两个阶段，具体阈值需要进一步研究确定)；3)上升阶段，从绿闪开始一直到相位时间结束。

为了比较每两个连续10 s间隔消散流率的差异，本文采用非参数检验的方法进行检验。从表2可知，前3个10 s绿灯间隔(0～＜30 s)的消散流率与其他间隔的消散流率之间存在显著差异。从30～＜40 s的连续10 s绿灯间隔至倒数第二个连续10 s间隔(AS 70～＜79 s，NJ 50～＜58 s)之间的非参数检验结果均大于0.05，即它们之间无明显差异。而在与最后一个间隔的比较中发现检验数值有大于也有小于0.05的值。这再次验证了排队车辆的消散过程可以分为3个阶段：

1）启动阶段(0～＜30 s的3个连续10 s绿灯间隔)；

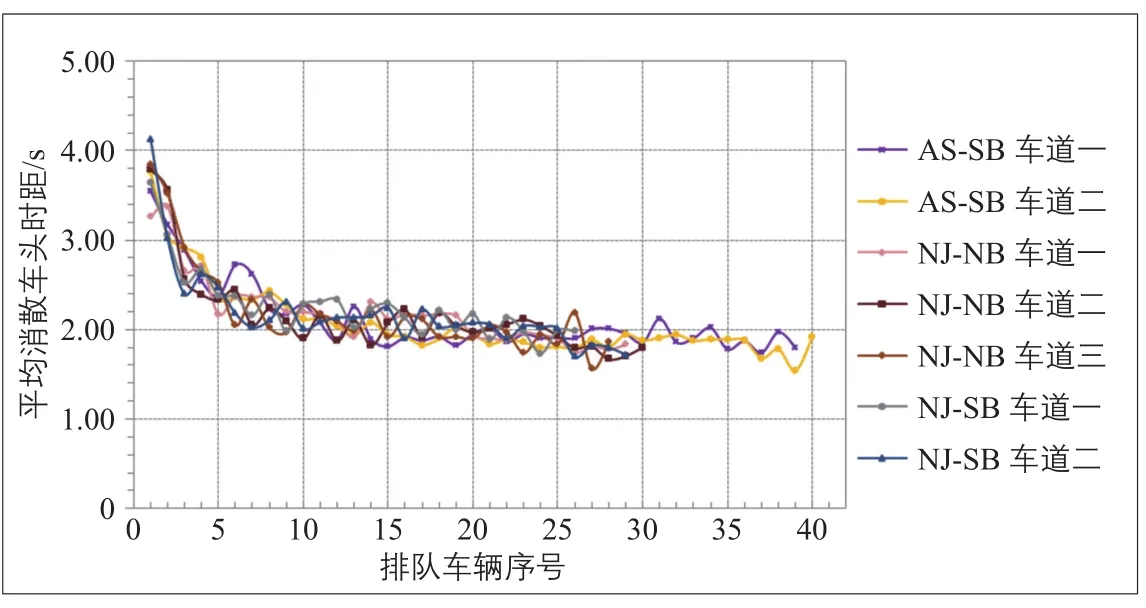
图2 各排队位置的平均消散车头时距Fig.2 Average discharge headwaysof each generated queue

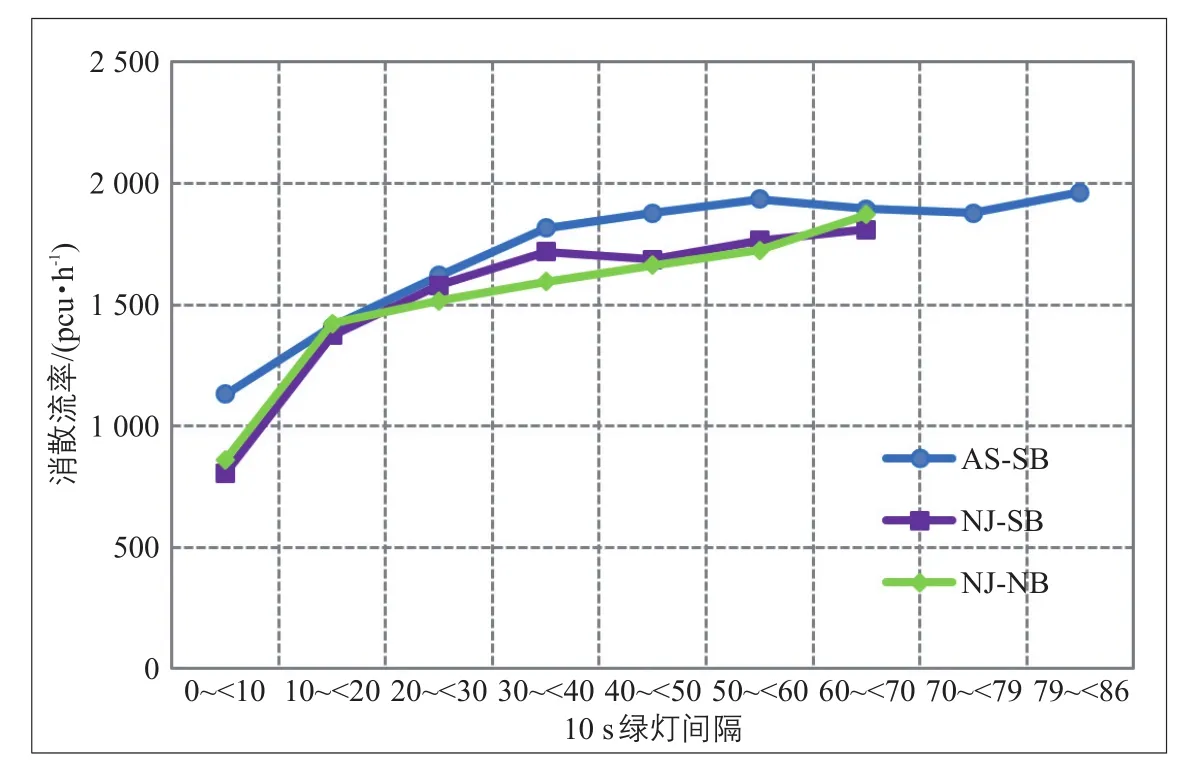
图3 以连续10 s绿灯间隔观测的消散流率Fig.3 Observed discharge flow rates in every 10 selapsed green time

2） 稳定阶段(20～＜58 s或者20～＜79 s的10 s绿灯间隔)；

3）上升阶段(最后一个时间间隔，即绿闪开始到全红结束的时间间隔)。

上述分析可看出，中国城市道路交叉口长周期倒计时信号控制下的排队消散特性与传统的假设不同(见图4)。

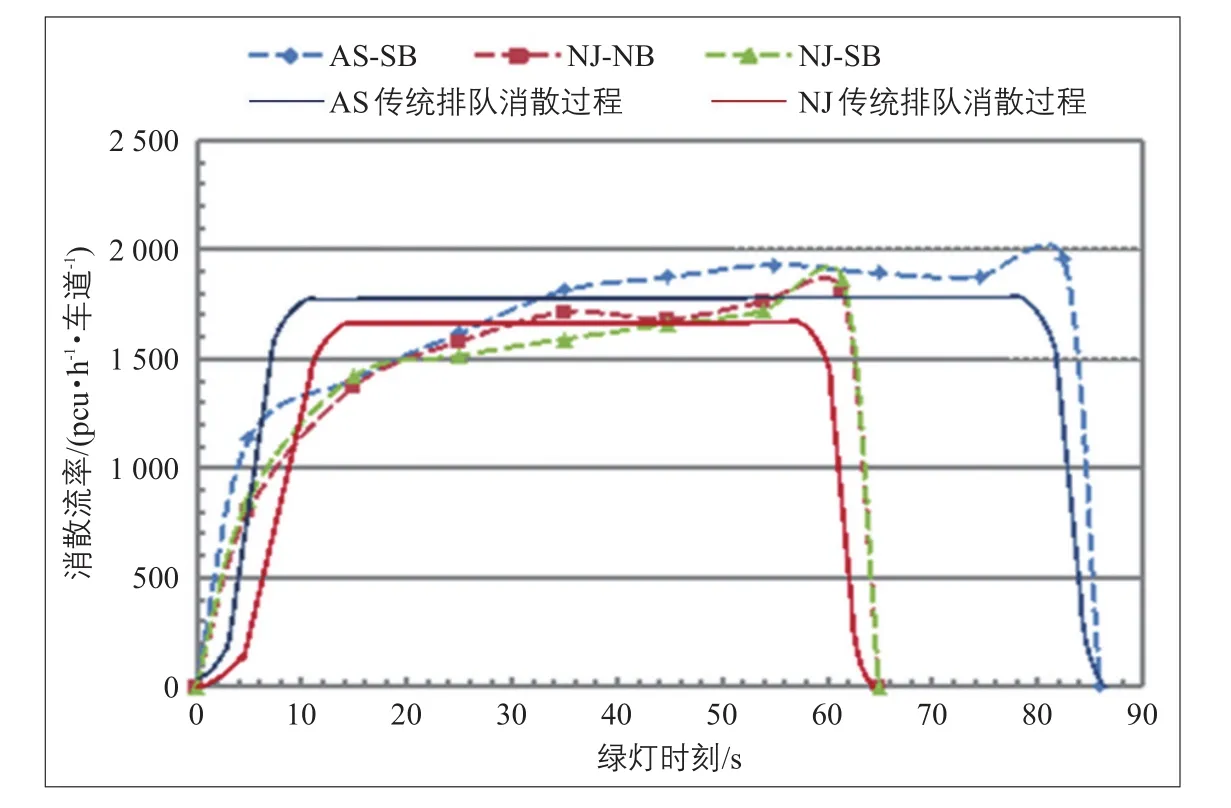
图4 排队消散特性与传统理论假设的区别Fig.4 Differencesbetween queue discharge patternsand conventionalassumptions

2.2 鉴别排队消散特性

2.2.1 鉴别方法

将城市道路交叉口长周期倒计时信号控制下的排队消散特性分为启动、稳定和上升3个阶段。为确定各阶段分割区间，需采用一定分割方法。考虑到排队车辆消散是车辆跟驰过程，连续而有序，与有序样品类聚方法的理论假设一致，故采用有序样品类聚法进一步鉴别排队消散特性。

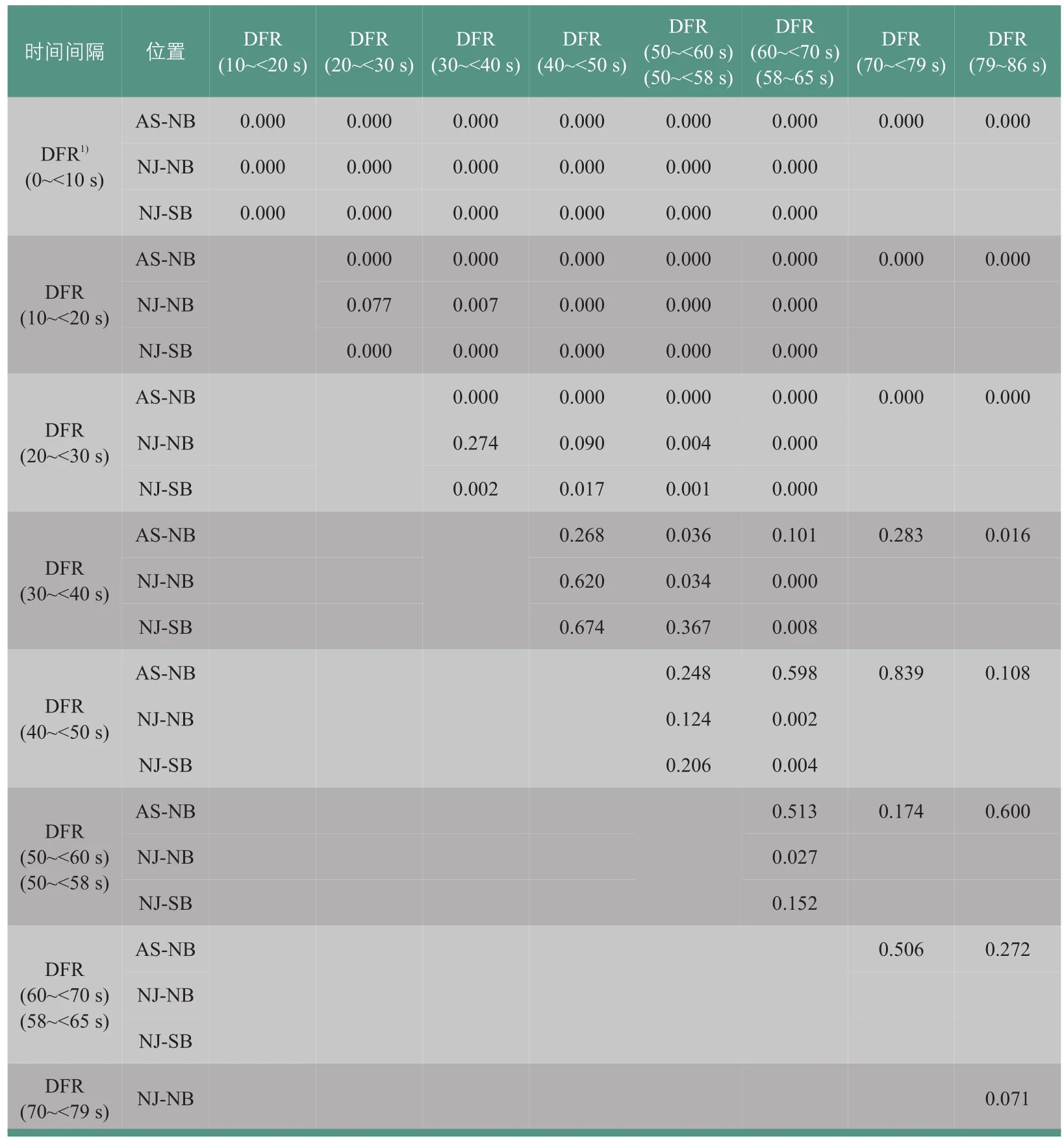
表2 10 s连续间隔消散流率的双样本K-S检验Tab.2 Two-sample K-Sanalysisof10 s-intervaldischarge flow rates

有序样品聚类法通过4个主要步骤确定最优分割：分类直径、误差函数、确定最优化分割数和确定最优分割间隔点，过程如下：

1）分类直径。

某一类包含的样品有{yi,yi+1,…,yj}，其中1≤i,j≤n，平均值

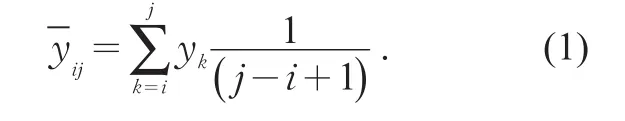
定义分类直径

2）误差函数。

误差函数

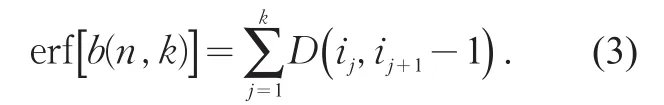
误差函数越小，同类样本差异越小，不同类之间差异越大。b( )n,k表示将n个有序样本分为k类的一种分法。当保持n和k不变，达到最小值时获得最优分割。误差函数是一个迭代公式。

3）确定最优分割数。

为获得最优分割数，引入最优分割系数β作为优化评估的指数，

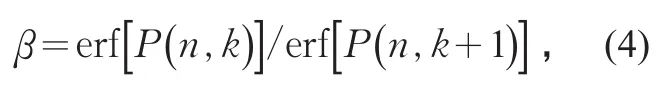
式中：P(n,k)是将n个样本分为k类时误差最小的分割方法。显然，β＞1，β越大说明样品分割点应该分成k+1段而不是k段。当β值接近1时，则不需要把样品分成k+1段，可认为k段是最优分割数。

4）确定最优分割间隔点。

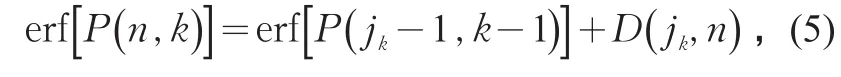
式中：jk为k+1和k之间的最优分割点。于是得到有序样本分为k类的最优方法。同样，根据公式(6)可以找到jk-1是k-2和k-1之间的最优分割点，

依此类推可以得到所有的分割种类和最优分割

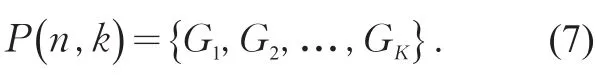
2.2.2 结果分析

针对5 s间隔的平均消散流率进行有序样本聚类分析。NJ和AS的整个相位被分为14和18个5 s间隔。为了与绿闪和黄灯时刻相匹配，NJ的55～65 s间隔被分为3个间隔即55～＜58 s、58～＜61 s(绿闪间隔)和 61～＜65 s(黄灯和全红间隔)，AS的75～＜86 s被分为75～＜79 s、79～＜82 s(绿闪间隔)、82～＜86 s(黄灯和全红间隔)。有序样品聚类法通过Matlab程序实现，结果见表3。

同时结合连续10 s绿灯间隔的驶出率特性，选择了3段的最优分割，并将这3个分段认为是两个阶段，即以第6个5 s间隔结束(30 s)为两个阶段的分界点(见表3)。这样划分的原因是：无论从10 s还是5 s连续间隔消散流率都可以得到前30 s消散流率处于上升阶段，并且在第6个5 s间隔处达到一致的分界点。将30 s前认为是消散流率的启动阶段，30 s后认为是排队消散的稳定阶段。虽然绿闪启亮后消散流率出现上升趋势，但相对于整个排队消散过程并不显著，所以将其一同归入稳定阶段。

3 结果分析

上述讨论表明，城市道路交叉口长周期倒计时信号控制下的排队消散特性与传统理论所描述的不同，这可能不是一个随机现象，而是车辆跟驰的一个固有属性。现行的通行能力和延误的估计方法均以稳定的消散流率(即饱和流率)为基础。然而，倒计时信号控制的消散流率在启动阶段比传统假设大得多，则传统的通行能力估计方法可能要重新评估。因此，本文验证了传统通行能力估计算法HCM 2010的误差大小，并提出简单线性法、抛物线法和两段线法来提高通行能力的估计精度。

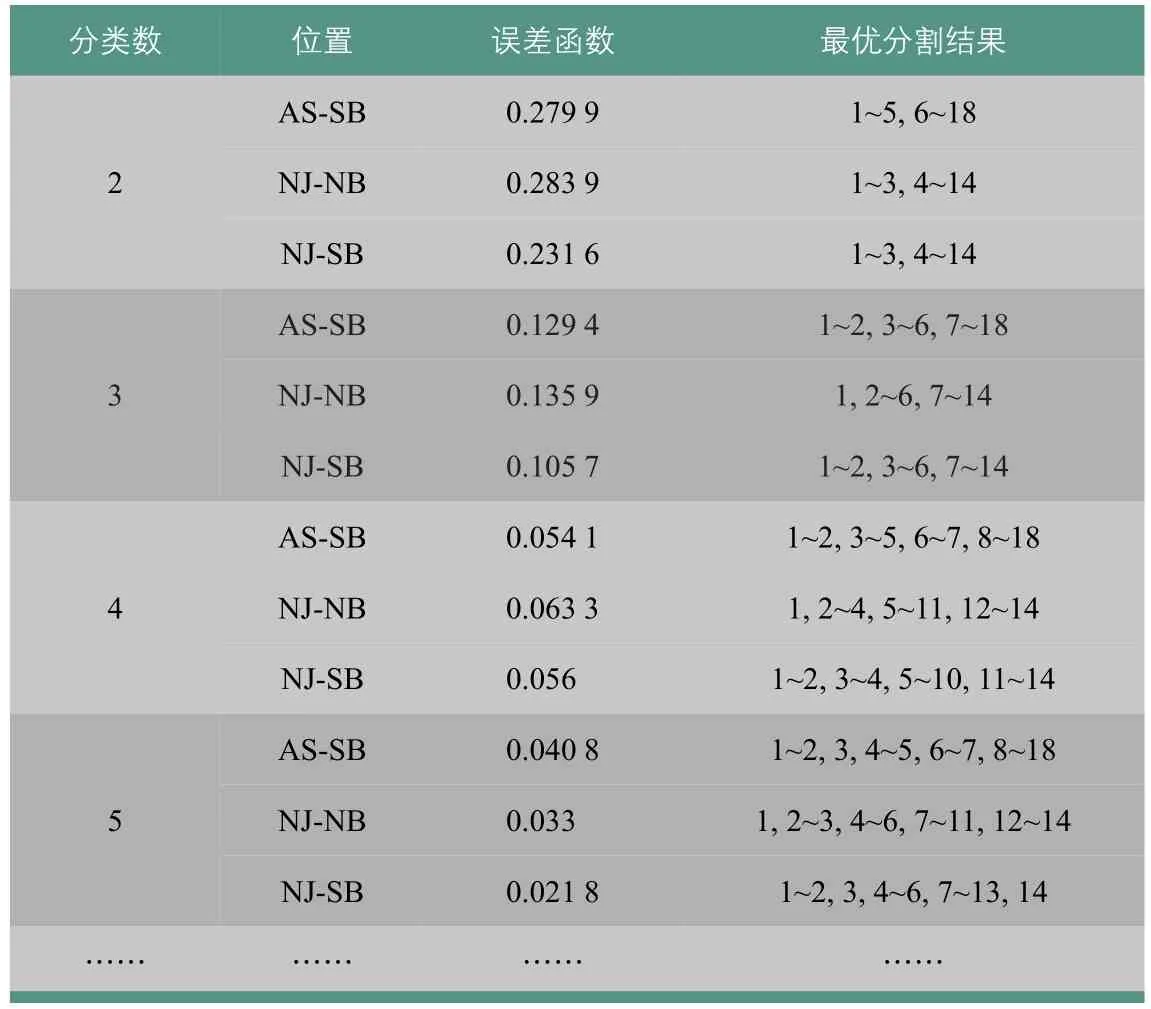
表3 分割结果和误差Tab.3 Resultsof subsection and errors

3.1 备选方法

首先，根据HCM 2010列出传统通行能力估计的计算方法：

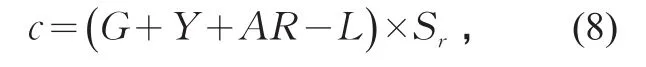
式中：c为通行能力/(pcu·h-1·车道-1)；G为绿灯时长/s；Y为黄灯时长/s；AR为全红时长/s；L为损失时间/s；Sr为流率/(pcu·s-1)。

本文提出3种备选通行能力估计方法如下：

1）简单直线拟合。

根据平均累计车辆数与相对应的相位时刻进行线性拟合，得到

则通行能力可以通过下式计算：

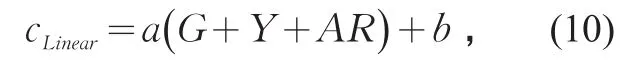
式中：x为经过的绿灯时长/s；f(x)为经过绿灯时长x时通过的累计车辆数/pcu；a，b为回归参数。

2）抛物线拟合。

根据平均累计车辆数与相对应的相位时刻进行抛物线拟合，得到

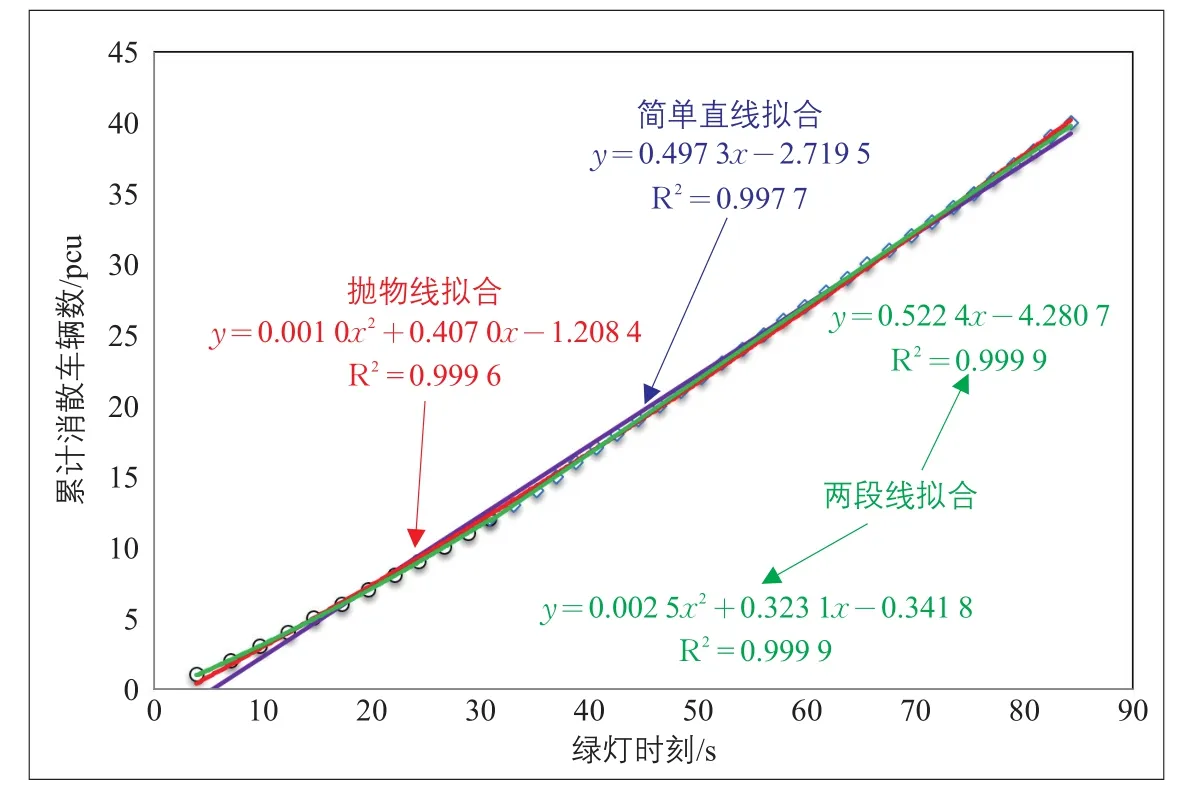
图5 3种备选方法示例Fig.5 Illustration of threeproposedmethods

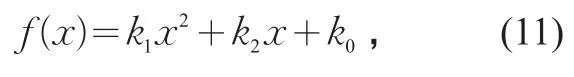
则通行能力可以通过下式计算：

式中：Lclt为清空损失/s；k1，k2，k0为回归参数。

3）两段线拟合。

基于上文的最优分割结果，以30 s为两段分割，对平均累计车辆数与相对应的相位时刻进行拟合。则通行能力计算如下：

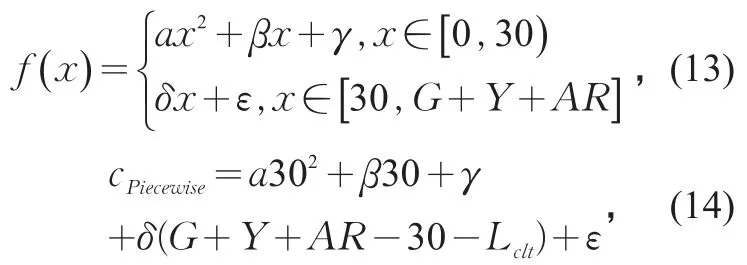
式中：a，β，γ，δ，ε为回归参数。

以AS-SB为例，拟合方程如图5所示。

3.2 不同方法对通行能力的估计和比较

根据实测数据使用4种方法对通行能力进行估计，据此比较估计精度。在HCM 2010估计通行能力的方法中使用的损失时间和清空损失由实际数据得到，分别是：AS损失时间7.09 s、清空损失2.87 s；NJ北进口道损失时间7.24 s、清空损失2.29 s；NJ南进口道损失时间8.14 s、清空损失2.12 s。

为了评价4种通行能力估计方法的误差，使用以下两个统计量：平均绝对百分误差(MAPE)和均方根误差(RMSE)。

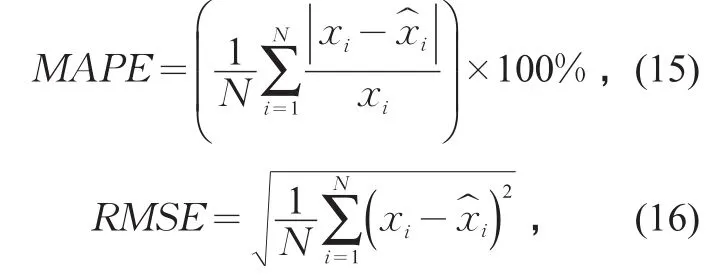
式中：xi为每个周期样本观测的消散车辆总数/pcu；为每个周期样本估计的消散车辆总数/pcu；N为总的周期样本数。

表4为交叉口3个进口道的实测通行能力与4种方法估计结果的统计比较，说明在城市道路交叉口长周期倒计时信号控制的情形下，HCM 2010通行能力估计值的RMSE偏大，每车道绿灯小时当量小汽车通行能力普遍大于50辆，当扩展至整个交叉口时该误差更大。但同时其MAPE值小于5%，从统计意义上来讲，可认为HCM方法有意义。

本文提出的3种备选方案均表现出比HCM 2010更好的适用性，特别是抛物线法和两段线法估计通行能力的RMSE值均小于30 pcu·h-1。样本周期的估计偏差如图6所示，可知HCM方法的估计值距离最大，两段线和抛物线的估计值则更接近实际。因此，在中国城市道路交叉口长周期倒计时信号控制下，HCM 2010的通行能力估计方法有一定的适用性，但误差较大，而两段线法和抛物线法更为准确。

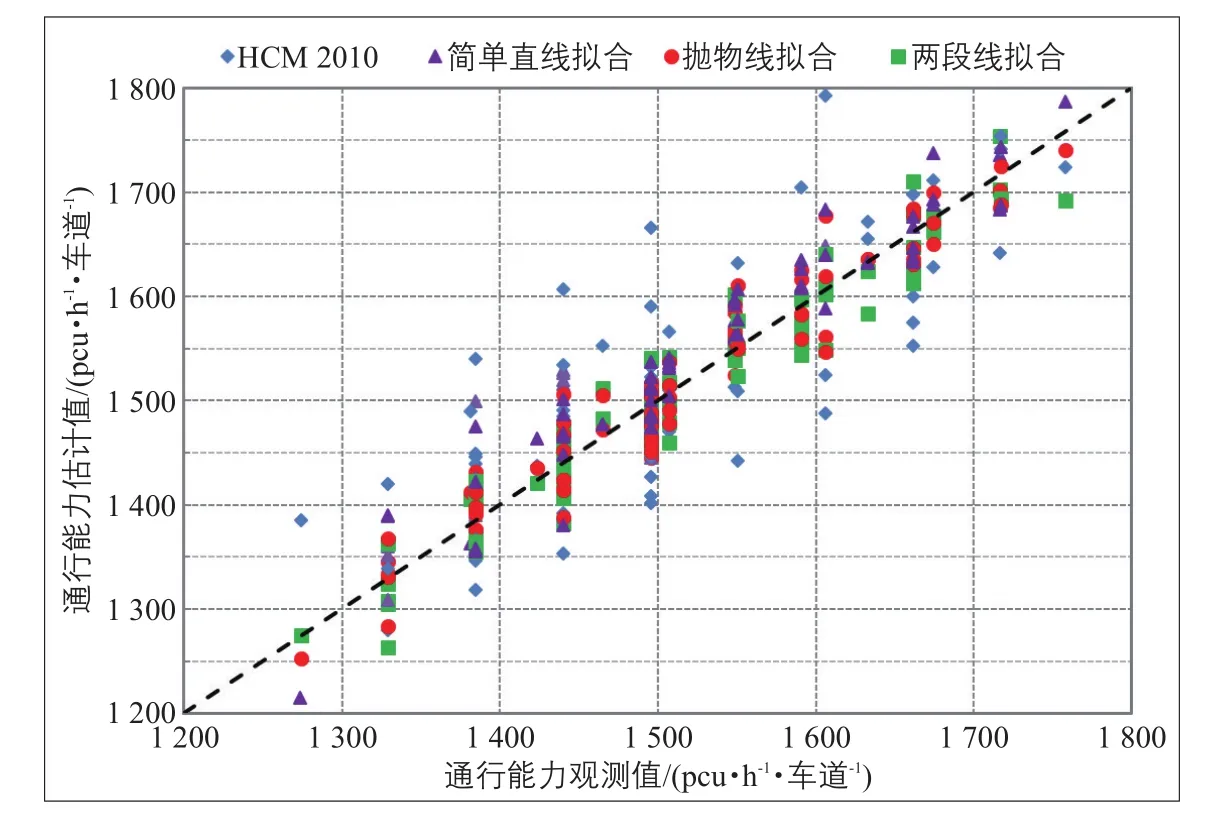
图6 不同方法的通行能力估计误差Fig.6 Estimation errorsof differentestimationmethods

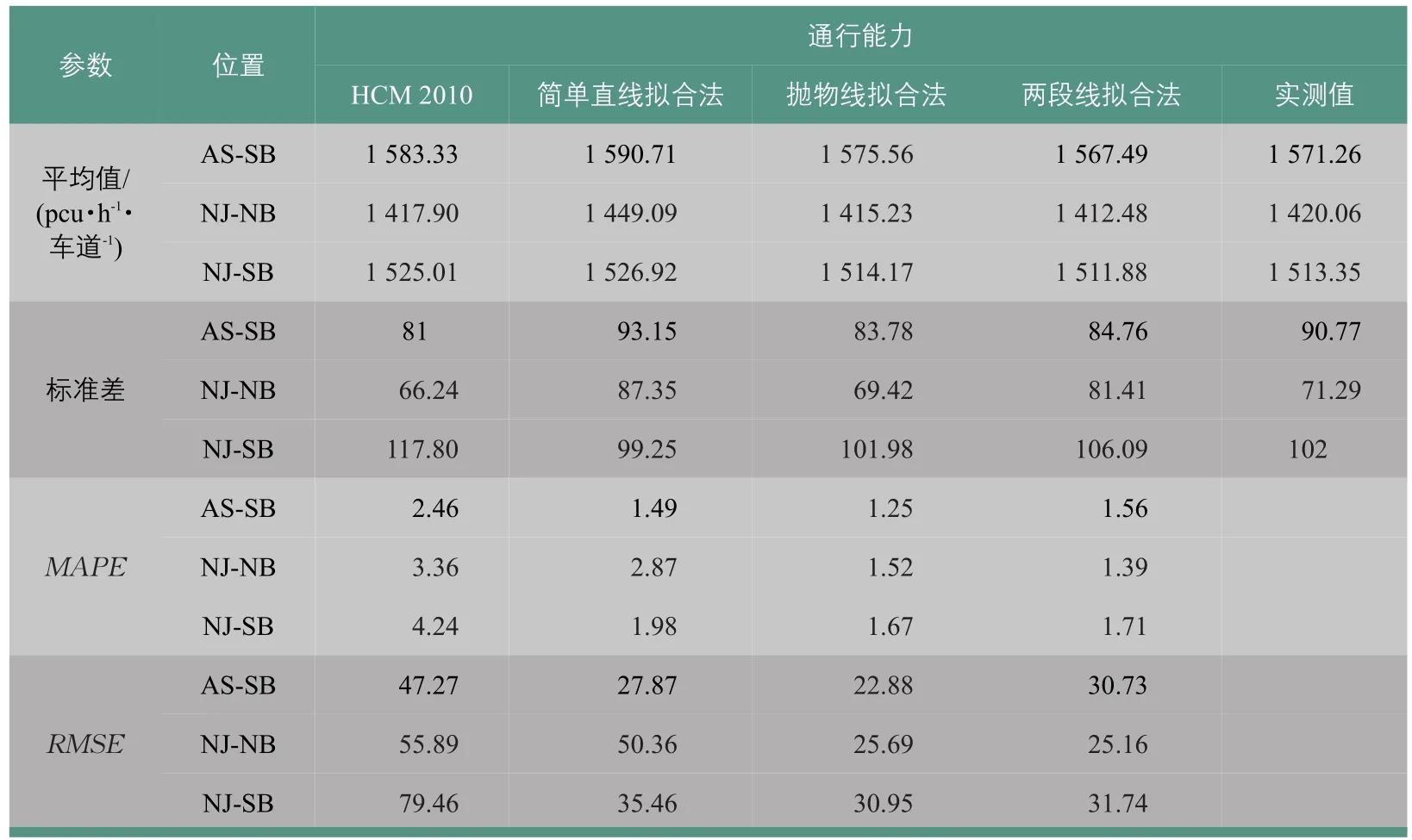
表4 不同方法估计与实测通行能力Tab.4 Comparison of the estimated capacitiesof threemethodsand the observed capacity

3.3 敏感性分析

为比较两段线拟合方法和HCM 2010方法在不同相位时长下估计的通行能力差异，本研究基于AS进行敏感性分析。两种方法的差异见图7。

当相位时长小于50 s时，HCM 2010方法估计的通行能力更小。出现这个现象的原因可能是在倒计时情形下，绿灯初期就有一个较高的消散流率，而HCM 2010假设的消散流率较低(见图4)。然而，当相位时长大于50 s时，HCM 2010估计的通行能力大于两段线法。这可能是因为HCM 2010认为在第4辆车之后即达到饱和流率，所以高估了实际通行能力。

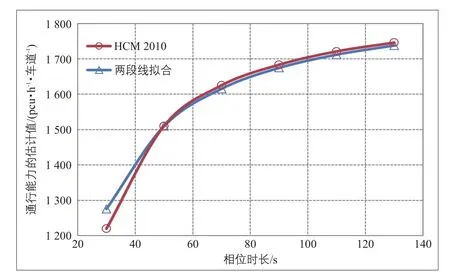
图7 两段线拟合与HCM 2010方法对不同相位时长的敏感性分析Fig.7 Sensitivity analysisof capacity estimation between Quadratic Linear Method and HCM 2010 under differentoffset length

4 结论与展望

本文基于天津市2个典型长周期倒计时信号控制交叉口3个进口道7条直行车道的实测数据，研究中国独特的长周期倒计时信号控制对排队消散特性的影响。其排队消散特性可以分为3个阶段：启动阶段(从绿灯启亮到30 s的绿灯间隔)，稳定阶段(从30 s的绿灯时刻到绿闪开始)和上升阶段(从绿闪开始到本相位结束)。由于在更为详细的统计分析中表明，相对于整个排队消散过程上升阶段并不显著，故本文建议在实际的数据处理中将这一阶段归入稳定阶段。

基于识别的排队消散特性，本文提出3个备选通行能力估计方法，即简单直线拟合、抛物线拟合和两段线拟合，并与传统的HCM 2010方法进行误差比较。结果表明，HCM 2010的通行能力估计方法有一定的适用性，但误差较大，而抛物线法和两段线法估计的通行能力更为准确。

然而，本研究只是针对城市道路交叉口长周期和倒计时情形下排队特性的初步研究，还需要进行大范围的实证研究，包括有无倒计时和长短周期的实地数据对比。同时，也需要从更加微观的驾驶行为分析方面解释出现该排队消散特性的原因。

[1]Akcelik R.Guide to Traffic Engineering Practice Series∶Part7∶Traffic Signals[R].Sydney∶Austroads,2003.

[2]Transportation Research Board.Highway Capacity Manual(HCM)[R].Washington DC∶Transportation Research Board,National Research Council,2010.

[3]Lee H S,Do TW.Saturation Headway of Through Movement at Signalized Intersections in Urban Area[J].Journal of Transportation Research Society of Korea,2002,20(5)∶23-31.

[4]Tang K,Nakamura H.An Analysis on Saturation Flow Rate and Its Variability[C]//The 11th World Conference on Transport Research.University of California,Berkeley,June24-28,2007.

[5]Boumediene A,Brahim i K,Belguesm ia N,Bouakkaz K.Saturation Flow Versus Green Time at Two-Stage Signal Controlled Intersections[J].Transport,2009,24(4)∶288-295.

[6]Khosla K,James CW.Saturation Flow at Signalized Intersections During Longer Green Time[J].Transportation Research Record∶Journal of the Transportation Research Board,2006(1978)∶61-67.

[7]Lin FB,Chang CW,Tseng PY.Errors in Capacity and Tim ing-Design Analyses of Signalized Intersections in the Absence of Steady Queue Discharge Rates[J].Transportation Research Record∶Journal of the Transportation Research Board,2007(2027)∶85-90.

[8]Chodur J,Ostrowski K,Tracz M.Impact of Saturation Flow Changes on Performance of Traffic Lanes at Signalized Intersections[J].Procedia Social and Behavioral Sciences,2011,16∶600-611.

[9]Lum K M,Halim H.A Before-and-A fter Study on Green Signal Countdown Device Installation[J].Transportation Research Part F∶Traffic Psychology and Behaviour,2006,9(1)∶29-41.

[10]Chiou Y C,Chang C H.Driver Responses to Green and Red Vehicular Signal Countdown Displays∶Safety and Efficiency Aspects[J].Accident Analysis and Prevention,2010,42(4)∶1057-1065.

[11]Sharma A,Vanajakshi L,Rao N.Effect of Phase Countdown Timers on Queue Discharge Characteristics Under Heterogeneous Traffic Conditions[J].Transportation Research Record∶Journal of the Transportation Research Board,2009(2130)∶93-100.

[12]Sharma A,Vanajakshi L,Girish V,Harshitha M S.Impact of Signal Tim ing Information on Safety and Efficiency of Signalized Intersections[J].Journal of Transportation Engineering,2012,138(4)∶467-478.

[13]Dong Sheng,LiKepeng,Fu Xiaoyan,Sun Jian.Non-Motorized Vehicles'Driver Behavior w ith Flashing Green and Green Countdown at Intersections∶A Comparative Study[C]//The 90th AnnualMeeting of Transportation Research Board.Washington DC,January 23-27,2011.

[14]Tang K,Dong S,Wang F,NiY,Li K.Driver Behavior of E-Bikes at the Onset of Green and Yellow at Signalized Intersections in China[J].Transportation Research Record∶Journal of the Transportation Research Board,2012(2846)∶85-96.

Im pacts of Signalw ith Long Cycle and Duration Countdown on Queue Discharge at Signalized Intersections

ZhaoWei,Xu Hanqing
(Tianjin Municipal Engineering Design&Research Institute,Tianjin 300051,China)

∶Long cycle and duration countdown are two unique characteristics of signalized intersections in China by comparison to those developed countries.This paper empirically investigates the impacts of such two characteristics on queue discharge at signalized intersections.For this purpose,seven traffic lanes at two typical intersectionsw ith long cycle and duration countdown are selected as study sites in Tianjin.The results show that the discharge process of queuing vehicles can be divided into three stages∶start-up stage,stable stage,and rising stage.The ordered samples clusteringmethod isused to identify the three partitions in which the findings are distinguished from the conventionalassumption of capacity estimationmethodologies,namely HCM 2010,the adaptiveness of traditionalmethods are thus analyzed.Furthermore,Piece-Wise Linear Method,Quadratic Linear Method,and Simple Linear Method are proposed to implement a better capacity estimation.The comparison results suggesta relatively more precise solutions from Piece-Wise LinearMethod and Quadratic LinearMethod where the RMSE is less than 30 pcu/h.

∶urban transportation;signal control;queue discharge characteristics;capacity;ordered samples clustering;long cycle;duration countdown

∶

1672-5328（2016）06-0067-08

U491.2+6

A DOI∶10.13813/j.cn11-5141/u.2016.0611

2014-12-23

赵巍(1982—)，男，辽宁鞍山人，硕士，高级工程师，主要研究方向：交通规划及交通设计。E-mail∶573291802@qq.com