带电螺线管磁场的数值研究

向 茜，王世庆，李自成，李兴红，候景景

（1．成都理工大学 工程技术学院 核工程与高新技术研究所，四川 乐山 614000；2．核工业西南物理研究院，四川 成都 610041；3．中核核电运行管理有限公司，浙江 嘉兴 314300）

大学生园地

带电螺线管磁场的数值研究

向 茜1，2，王世庆1，2，李自成1，2，李兴红1，2，候景景3

（1．成都理工大学 工程技术学院 核工程与高新技术研究所，四川 乐山 614000；2．核工业西南物理研究院，四川 成都 610041；3．中核核电运行管理有限公司，浙江 嘉兴 314300）

从毕奥-萨伐尔的基本定律出发，引入有效半径、有效空间位置和有效空间取向等概念，通过比较电流环和磁偶极场的远场近似计算与严格的带电螺线管磁场的计算结果，采用优化螺线管结构和构建计算模型，可以有效地克服螺线管本身带来的空间磁场有限长度效应．在有效空间范围内进行数值模拟的结果表明，磁偶极场的远场近似不仅可以满足磁场计算的精度要求，而且具有极高的计算速度．可以实时地实现具有多带电螺线管复杂结构的电磁计算，满足电磁空间定位和电磁导航的要求．

带电螺线管；磁场计算；有效半径；有效空间位置；有效空间取向

本文是以具有典型工程应用的医学电磁导航外科手术系统的电磁辐射系统与电磁导航区域为研究对象，研究密绕多层带电螺线管在导航区域产生的磁场强度的计算方法．这种研究方法在工程应用中具有广阔的拓展空间［1-5］．在有效空间范围内，通过电流环和磁偶极场的远场近似计算与严格的螺线管磁场计算进行比较，引入有效半径，有效空间位置和有效空间取向等概念，优化螺线管结构和构建计算模型，可以有效地克服螺线管本身带来的空间磁场有限长度效应．

1 带电螺线管的计算模型

1．1带电螺线管的严格计算模型

将密绕多层带电螺线管线圈置于直角坐标系中，如图1所示，其内半径为 a，管长度为 L，线圈匝数为n，中心与坐标原点重合，在空间点P（x，y，z）处的磁感应强度B为

图1　密绕多层螺线管结构

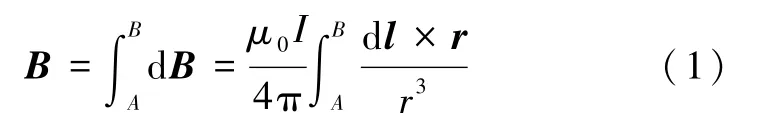
式（1）中dB为电流元在空间点P产生的磁场，μ0为真空磁导率，I为流过螺线管的电流，A和B分别为电流I流入和流出螺线管的起始点，dl是螺线管线圈绕组总长度l的线元，r=rP-r′是线元到空间点P的位置矢量，rP为坐标原点到空间点P的位置矢量，r′为坐标原点到线元的位置矢量.积分是沿螺线管线圈从电流I流入点A到流出点B的线积分.

除了位于螺线管轴线的空间点外，对于其他位置空间点P，要给出式（1）的解析解是十分困难的.假设密绕多层带电螺线管线圈的管长远大于线圈导线的半径时，在空间点P（x，y，z）处的磁感应强度B可以近似为n个不同位置、不同半径的电流环在空间位置点P（x，y，z）处的磁场叠加，有

1．2电流环近似模型

将密绕多层带电螺线管线圈等效为n个电流环叠加时，电流环置于直角坐标系中 xy平面，如图2所示，中心与坐标原点重合，环面法线与 z轴重合，电流环在空间点P产生的磁感应强度B环为

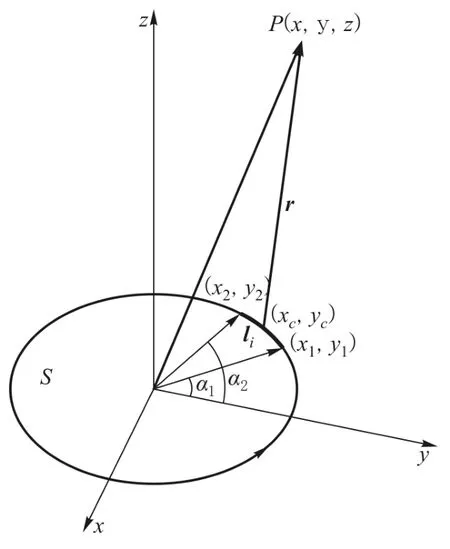
图2　xy平面上的电流环

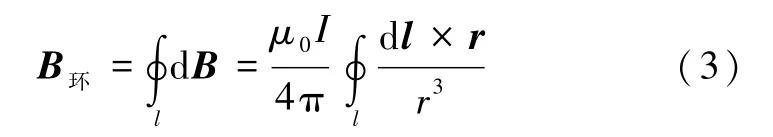
对式（3）沿闭合电流环积分，分别得到空间点P产生的磁感应强度的3个分量B环x、B环y和 B环z的解析表达式为［6］：

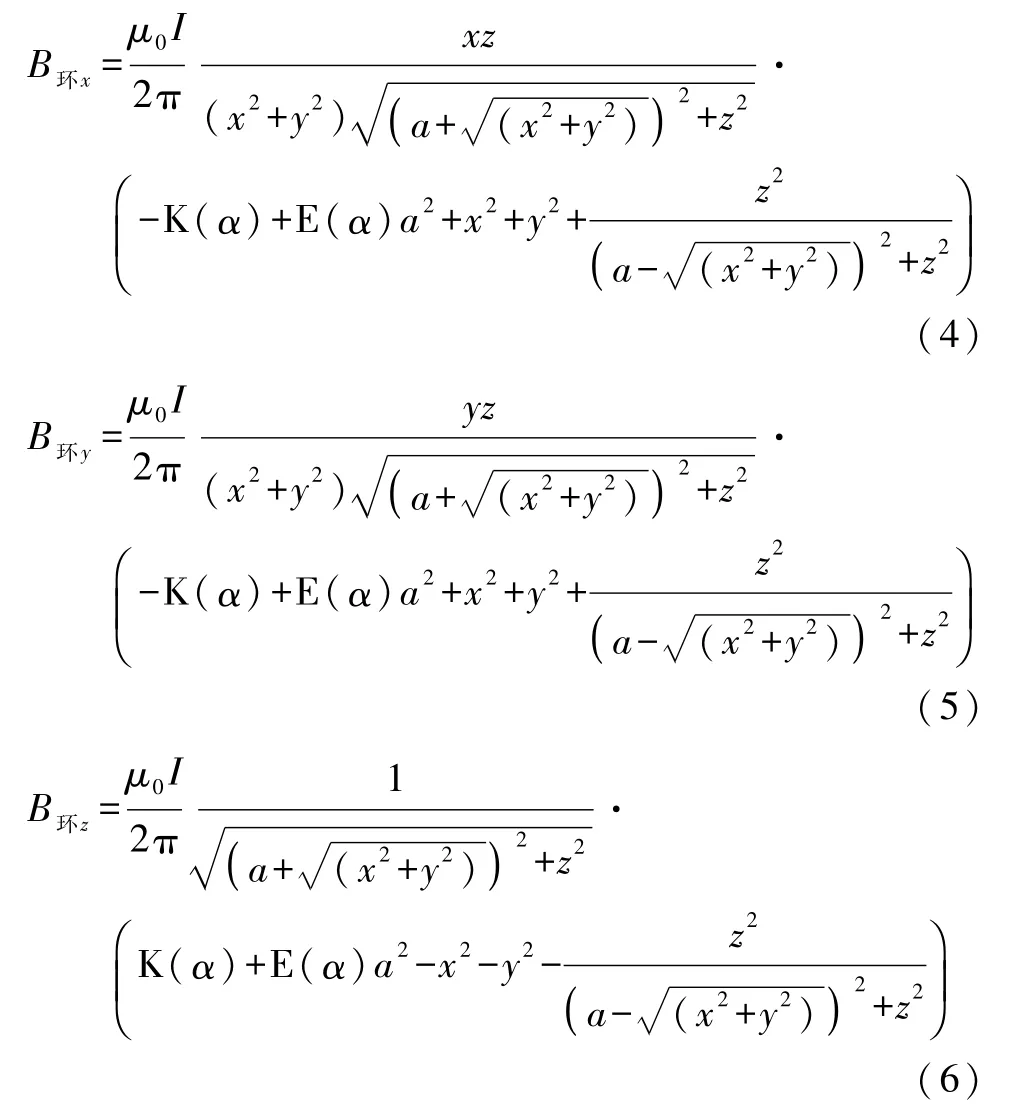
其中

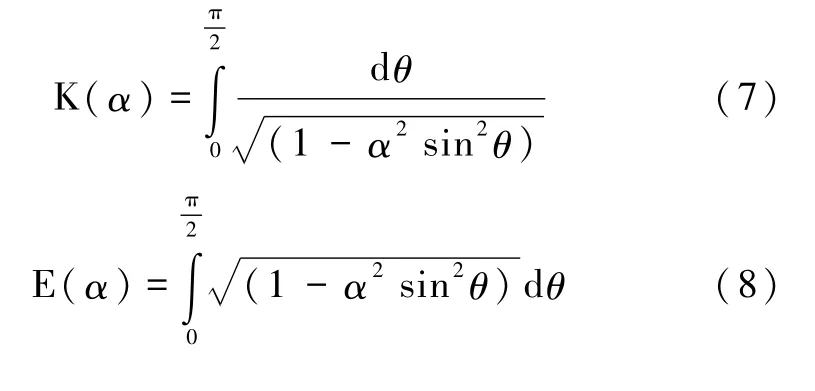
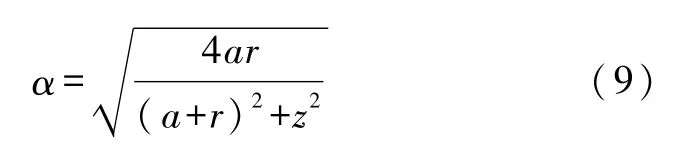
虽然从式（4）到式（6）给出了空间点 P处磁感应强度3个分量的解析解，但表达式太复杂，每个分量的计算都要面临处理椭圆积分，数学处理难度加大.

1．3磁偶极远场近似模型

当空间点P（r）到电流环中心的距离远大于电流环半径a时，磁偶极远场近似成立，如图3所示.

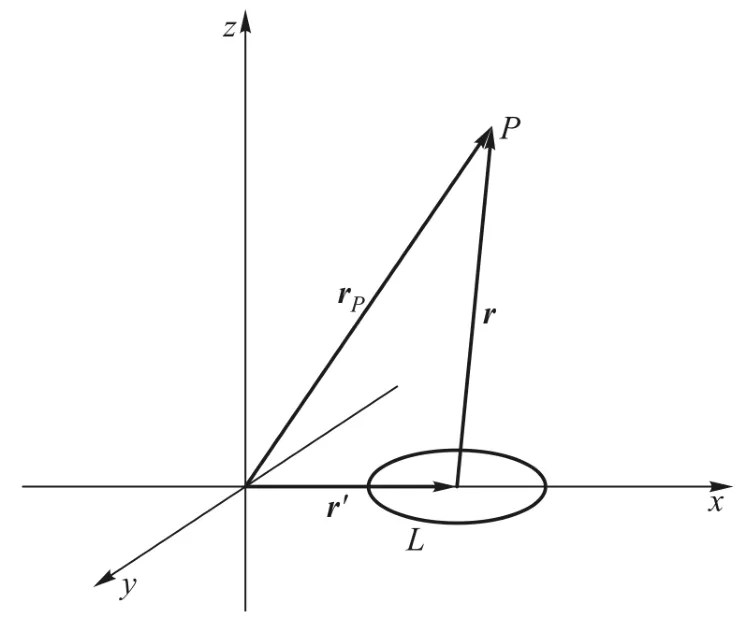
图3　磁偶极子不在坐标原点的模型

可以用空间点P（r）的磁偶极场取代电流环在该点产生的场.因此式（2）又可以表示为

图3表示不在坐标原点的磁偶极子，利用远场近似式可得空间点P（r）的磁感应强度［7］：

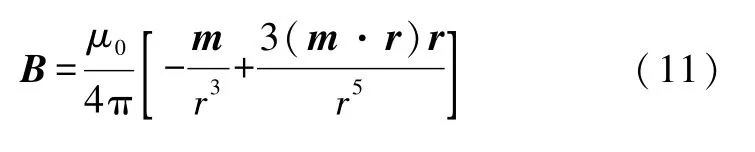
其中

S为电流环围绕的面积，以电流方向为准，S按右手定则确定面积的正向，m为磁偶极矩，r是磁偶极子的中心到空间点P的位置矢量，rp为坐标原点到空间点P的位置矢量，r′为坐标原点到磁偶极子中心位置的矢量.

2 计算方法

2．1带电螺线管磁场计算方法

如图1所示，改写密绕多层带电螺线管磁场计算式（1），空间P点的磁感应强度为

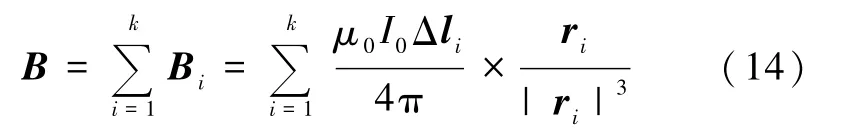
式（14）中Bi为密绕多层带电螺线管线圈绕组分为k段电流元中的第i段电流元I0Δli在空间点P产生的磁感应强度，ri是第 i段电流元 I0Δli到空间点P的位置矢量，求和是对整个带电螺线管线圈而言.

利用式（14）计算螺线管在空间 P点产生的磁场，需要计算遍及整个带电螺线管线圈的每个电流元，每一步计算都需要重新定位带电螺线管线圈的线元，及其与空间点P的相对位置矢量，然后进行相关的计算，因此计算量非常大，计算速度慢但精度高，故又称为严格计算法.在有实时要求的工程应用中，这种算法受到极大的挑战.

2．2电流环近似计算方法

式（2）给出了带电螺线管原理性的电流环近似算法，需要从螺线管线圈匝数1到n求和.我们引入有效半径，有效空间位置和有效空间取向等概念，构建一个新的电流环体系，使其满足如下条件：

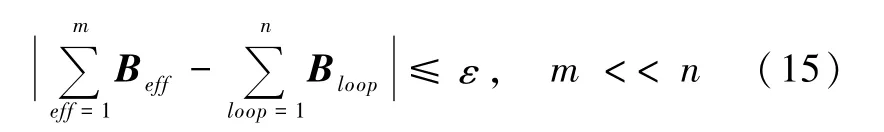
图4给出构建因子m=1密绕多层螺线管线圈近似为电流环的有效半径a，位于螺线管中平面电流环的有效空间位置O和由螺线管电流方向确定的电流环有效空间取向S.

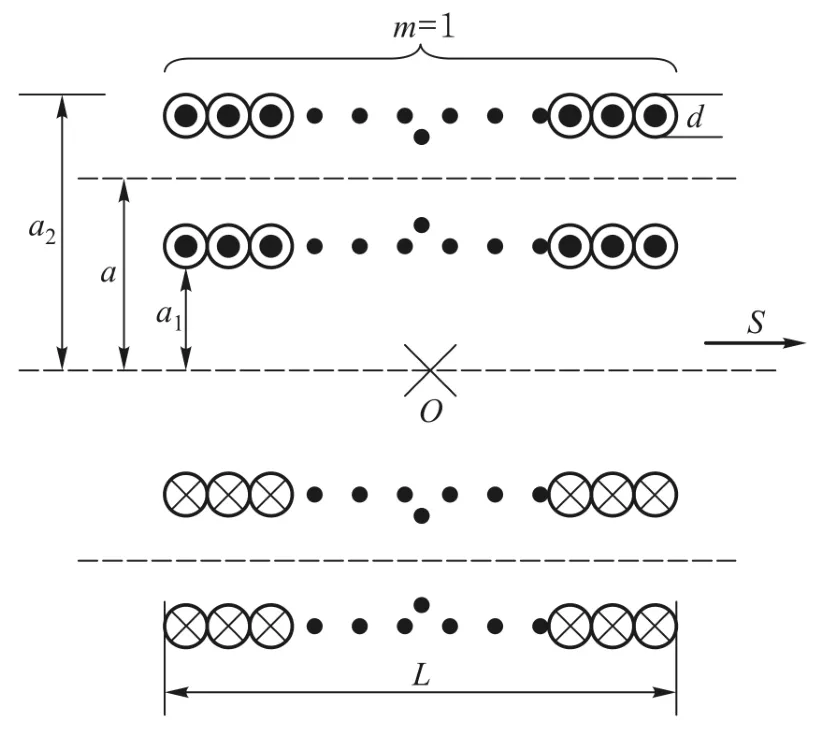
图4　构建因子m=1密绕多层绕组螺线管构建图

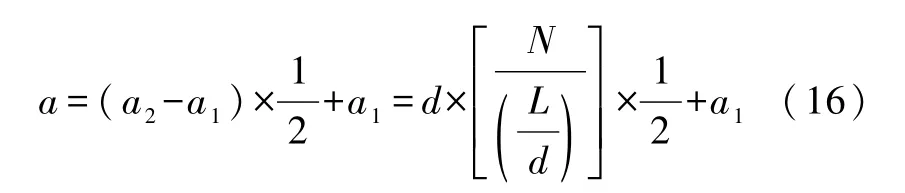
式（16）中a1为密绕多层螺线管线圈的内径，a2为密绕多层螺线管线圈的外径，d是线圈导线的直径，L是螺线管线圈的长度.为每层绕组的匝数.

改写式（3）计算m=1新构建电流环体系在空间P点的磁场为

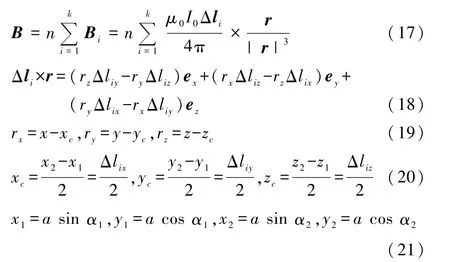
其中：Bi是将每匝电流环分为 k段电流元中的第 i段在空间点P产生的磁感应强度；I0Δli为每匝电流环中的第i段电流元；Δli在直角坐标系中的分量为（Δlix，Δliy，Δliz）.将式（18）—式（21）代入式（17）可以得出n匝电流环在空间产生的磁场分布.

同样可以采用类似的方法，构建因子m=2，3，…，m0的电流环体系.研究结果表明新构建的电流环体系可以大大提高计算速度，构建m=5的电流环体系，空间磁场的计算精度可达 0.01%.这种新构建的电流环体系在优化螺线管线圈的结构，克服螺线管线圈有限长效应起着十分重要的作用.

2．3磁偶极子远场近似计算方法

处理密绕多层带电螺线管线圈的磁偶极子远场近似法与电流环近似法完全相同，用上节类似的方法求出近似磁偶极子的有效半径，有效空间位置和有效空间取向，构建一个满足式（15）的磁偶极子体系.

图4给出构建因子m=1密绕多层带电螺线管线圈近似磁偶极子有效半径 a，位于螺线管中平面磁偶极子有效空间位置O和由螺线管电流方向确定的磁偶极子有效空间取向S.

m=1磁偶极子体系在空间P点产生的磁场为

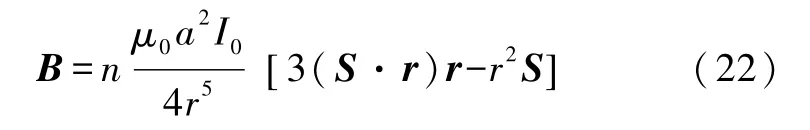
其中，n为螺线管线圈的总匝数，a为密绕多层带电螺线管线圈的有效半径，S为螺线管线圈的有效空间取向，r由式（13）得到.

同构建的电流环体系一样，同样可以采用类似的方法，构建因子m=2，3，…，m0的磁偶极子体系.例如构建因子m=5的磁偶极子体系如图5所示.

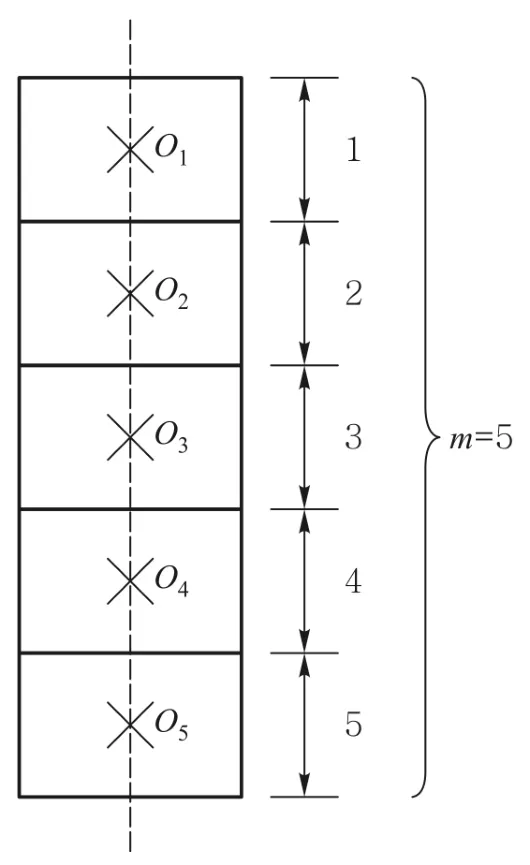
图5　构建因子m=5的磁偶极子体系

m=5磁偶极子体系在空间P点产生的磁场为

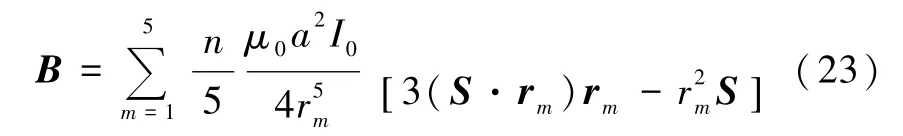
式中，n为螺线管线圈的总匝数，a为密绕多层螺线管线圈的有效半径，S为螺线管线圈的有效空间取向，rm为中心点 Om到空间点 P的位置矢量，由式（13）得到.

新构建的磁偶极子体系和新构建的电流环体系一样，具有相同的空间磁场计算精度，构建因子m=5的磁偶极子体系，计算精度可达0.01%.在优化螺线管线圈的结构和构建计算模型，克服螺线管线圈有限长效应等方面，有着和新构建的电流环体系一样的作用.然而计算速度比新构建的电流环体系快1到2个数量级，适合于各种实时电磁导航系统的应用.

3 仿真与讨论

为了验证算法的性能，本文用Visual Studio 2008计算多层绕组带电螺线管空间磁场分布（500×500× 500 mm3范围内），在有效空间内进行3种不同计算的比较，第一种是严格计算，第二种是电流环远场近似计算，第三种是磁偶极子远场近似计算．为了便于对计算方法的研究和计算结果的比较，将螺线管的中平面置于xy平面，原点位于（0，0，0）处，螺线管沿z轴放置.3种计算得到磁场分布均一致，如图6和图7所示显示空间磁场的3维分布.

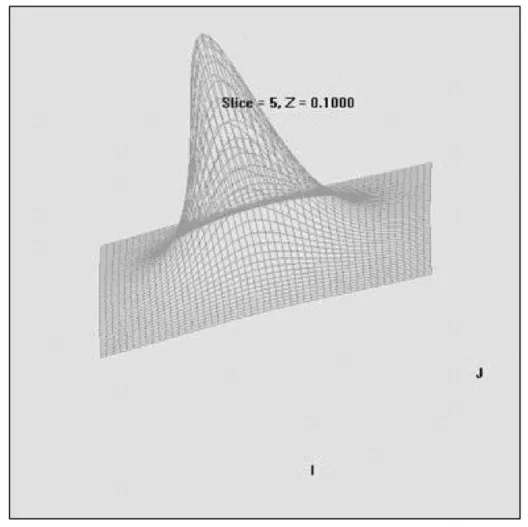
图6　xy平面上磁感应强度在3D空间的分布

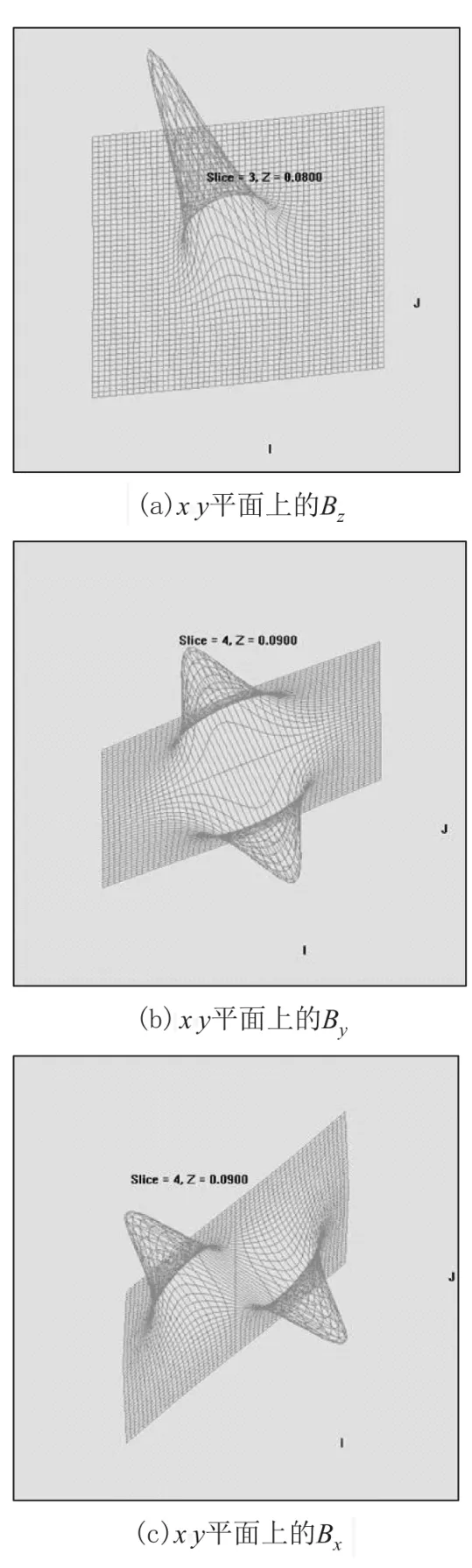
图7　磁感应强度各分量的3D空间分布

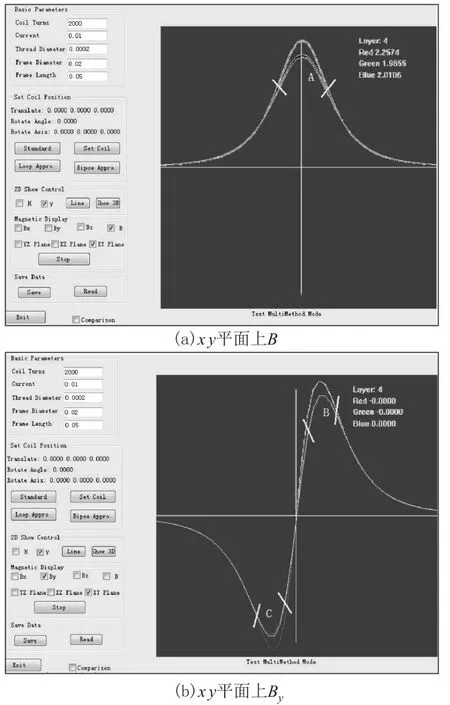
图8　构建因子m=1，3种方法计算结果的比较

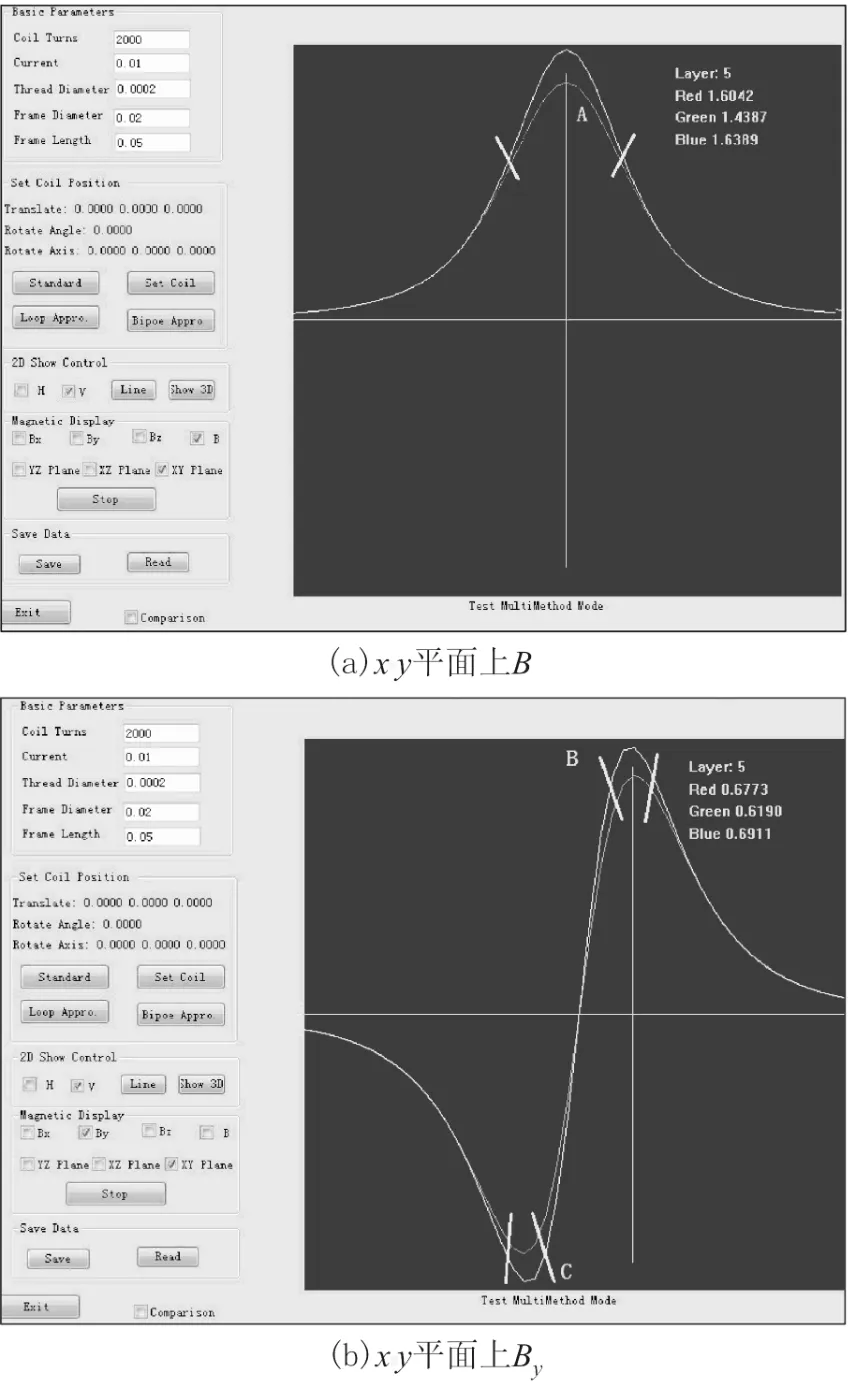
图9　构建因子m=5，磁偶极子体系磁场的计算结果比较

图8和图9给出由3种计算方法得到磁感应强度及其 y分量在 z=9．0 cm，y=0，沿 x方向从x=-25 cm到x=25 cm的变化．在图8中，构建因子m=1电流环体系的计算结果（绿线所示）和构建因子m=1磁偶极子体系的计算结果（蓝线所示）比较一致，但他们与螺线管严格计算的结果（红线所示）在A、B和C处都有明显的偏差.这种偏差来自于螺线管的有限长度L，而且随着螺线管的长度L加长，这种偏差越明显.重新构建m=5的磁偶极子体系近似计算与m=1的电流环近似计算和螺线管严格计算进行比较，结果如图9所示.新构建 m=5的磁偶极子体系磁场计算结果与螺线管严格计算的结果一致性已经相当好，这两条变化曲线几乎重合.因此随着构建因子m值越大，这两条变化曲线的偏差越小.

4 结论

本文通过研究带电螺线管磁场计算的3种方法，引入有效半径、有效空间位置和有效空间取向等概念，优化螺线管结构和构建计算模型，可以有效地克服螺线管本身带来的空间磁场有限长度效应.从创建的操作界面上可以直观地展示磁场分布特点及比较.解决了对多层绕组带电螺线管线圈在空间磁场计算的实用性问题.

［1］ 童国平．螺线管离散模型与连续模型的比较［J］．大学物理，2014，33（7）：15-16．

［2］ 唐劲飞，龚沈光，王金根．基于磁偶极子模型的目标定位和参数估计［J］．电子学报，2002，30（4）：614-616．

［3］ 师晓宙，胡超，向望华，等．用于骨科手术机器人的电磁定位方法［J］．传感技术学报，2011，24（11）：1569-1573．

［4］ 胡超，宋霜，阳万安，等．胶囊内窥镜位置方向磁场定位技术的研究［J］．集成技术，2012，1（1）：105-113．

［5］ 向茜，王世庆．六自由度电磁探测的快速数值算法［J］．计算物理，2013，30（5）：720-726．

［6］ Schneider．Measuring position and orientation using magnetic fields：United States Patent，6073043［P］．2000-6．

［7］ 俞允强．电动力学简明教程［M］．北京：北京大学出版社，1999：97．

Numerical study of the magnetic field of the charged solenoid

XIANG Qian1，2，WANG Shi-qing1，2，LI Zi-cheng1，2，LI Xing-hong1，2，HOU Jing-jing3
（1．Institute of Nuclear Engineering and Technology，Engineering＆Technica College，Chengdu University of Technology，Leshan，Sichuan 614000，China；2．Southwestern Institute of Physics，Chengdu，Sichuan 610041，China；3．CNNP Nuclear Power Operations Management Co．，Ltd，Jiaxing，Zhejiang 314300，China）

Based on the Boit-Savart law，the concepts of effective radius，effective spatial location and effective spatial orientation are introduced by comparing the far-field approximate calculation of charged current loops and the dipole magnetic field with the strict calculation of the magnetic field of the solenoids．By optimizing the solenoid structure and rebuilding，the computing model can overcome the limited length effect of the spatial magnetic field brought by the solenoid itself effectively．By simulating the system within the effective region，the result shows that the far-field approximate calculation of the dipole magnetic field not only meets the accuracy in magnetic field calculation but also has very fast calculation speed．The method can realize the magnetic calculation with the complex structure from many solenoids in real time and satisfy the real-time requirement of spatial positioning and electromagnetic navigation．

charged solenoid；magnetic field calculation；effective radius；effective spatial location；effective spatial orientation

O 441

A

1000-0712（2016）10-0029-06

2015-09-02；

2016-02-29

国家自然科学基金（11375055）、院级青年科学基金（c122014019）资助

向茜（1982—），女，四川省成都市人，讲师，硕士，主要从事远程医疗定位跟踪及应用电磁学研究工作.