大学物理中流体力学问题的计算机模拟研究
2016-12-12马增威汪志勇韦建卫刘改琴李锐峰
马增威,汪志勇,韦建卫,刘改琴,胡 南,李锐峰
(重庆理工大学 光电信息学院,重庆 400054)
大学物理中流体力学问题的计算机模拟研究
马增威,汪志勇,韦建卫,刘改琴,胡 南,李锐峰
(重庆理工大学 光电信息学院,重庆 400054)
格子玻尔兹曼模拟方法(Lattice Boltzmann Method,LBM)被广泛应用于流体力学问题的研究中,本文采用LBM方法对牛顿流体和非牛顿流体的泊肃叶流动进行了模拟,还通过模拟圆柱绕流问题演示了层流和湍流现象并阐明了雷诺数的概念.将LBM模拟结果与大学物理的相关流体力学知识相联系,不仅可以直观地解释抽象的流体力学概念,而且能够培养学生采用计算物理学手段解决实际问题的思维方式.
计算机模拟;牛顿流体;非牛顿流体;层流;湍流
近年来,随着计算机技术的不断发展,越来越多的课堂教学中采用现代化多媒体手段进行辅助教学,在提高课堂效率的同时扩大了学生的视野[1,2].计算机模拟在科学研究上已经具有了与理论和实验同等重要的地位,成为了研究自然界的第三种有效方法,若将计算物理的研究成果适当的引入到大学物理教学中,有助于学生理解大学物理课程中抽象和复杂的物理规律和现象[3-5].计算机模拟利用模型来研究一个系统的行为特征,实现对物理规律、现象的科学、严密的真实再现.模拟具有不受空间限制的特点,模拟尺度从宏观到微观,模拟方法包括有限元法、耗散力子动力学、格子玻尔兹曼方法、分子动力学及第一性原理;也不受时间限制,可模拟瞬间的物理过程并在较长的时间内进行展示.计算机模拟的上述特点,是其他辅助教学手段不可比拟的,不仅可以提高大学物理的教学效果,还可以培养学生采用计算物理方法解决实际问题的思维方式.将计算机模拟手段融入到大学物理教学中,必然对物理教师提出了新的要求,教师要针对大学物理课程中的难点内容,结合具体实例编写程序,这是计算机模拟融入大学物理教学的关键.格子玻尔兹曼模拟方法 (Lattice Boltzmann Method,LBM)被广泛应用于流体力学问题的研究中,本文针对大学物理中流体力学部分的概念和问题,采用LBM方法模拟牛顿流体和非牛顿流体的泊肃叶流动及圆柱绕流问题,并演示了层流、湍流和卡门涡街现象.
1 LBM模拟方法的理论介绍
LBM方法的基本思想是在简化连续玻尔兹曼方程的同时,保留流体力学的本质特征,理论基础是从微观动力学方程出发推导出宏观流体力学方程,推导中一个重要的假设就是分子混沌条件,即相互碰撞的分子间统计独立.借助这一假设得到近似玻尔兹曼输运方程,再使用 Chapman-Enskog多尺度展开方法得到Navier-Stokes方程,同时得到黏度计算式.LBM方法具有以下特点:1)程序设计简单,运算效率高;2)适合于大规模并行计算;3)可以处理复杂的边界条件.玻尔兹曼方程通常采用Bhatnagar-Gross-Krook(BGK)模型:
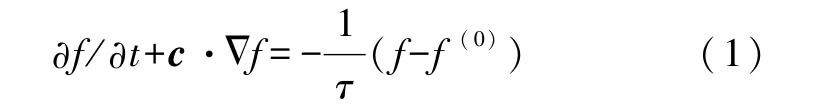
其中f为分布函数,f(0)为平衡分布函数,τ为弛豫时间,c为速度.首先在速度空间选取有限的方向,完成对速度空间的离散化:
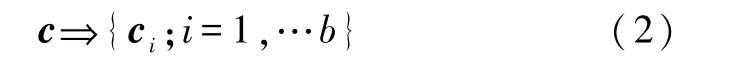
ci为格子速度,b为选取离散速度方向的个数,离散化后的分布函数用fi(r,t)表示,再进一步对时空进行离散化,空间间隔Δr、时间间隔Δt及格子速度ci有如下关系:

根据有限差分的方法得到单松弛时间的离散格子玻尔兹曼方程:
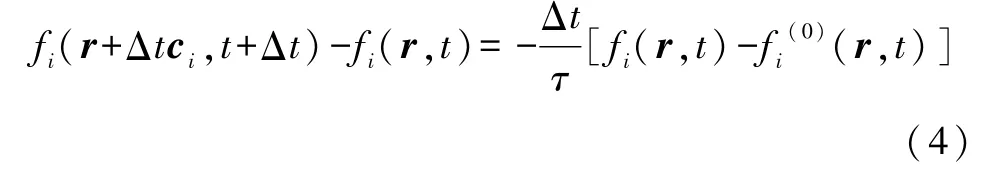
离散格子玻尔兹曼方程(4)用于计算流场中的新的分布函数,然后再更新流场中的密度ρ(r,t)和速度uα(r,t):
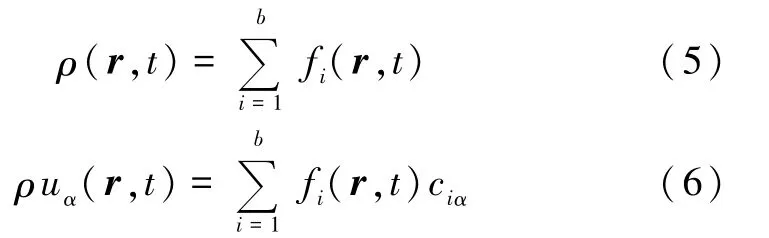
以上是对LBM方法的基本理论和建模过程的简单介绍,对每个具体模型还要具体推导黏度计算公式.在LBM方法中,单松弛时间(SRT)BGK模型在模拟复杂边界体系时会出现数值稳定性和黏度依赖性的缺点.多松驰时间(MRT)模型可以消除SRT模型中的缺点,并提高计算精度[6].我们所采用D2Q9 MRT模型中,每个格点有9个速度分布函数,可以写成如下形式:
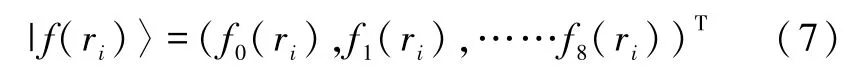
分布函数 f(ri)通过变换矩阵 M映射到 Moment空间(即物理量空间),分布函数在两个空间的转化关系为
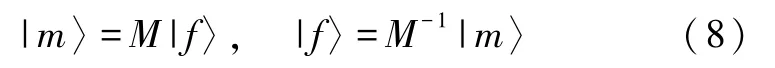
其中|m〉为Moment空间中的分布函数.在Moment空间根据下面的碰撞方程实现碰撞演化:
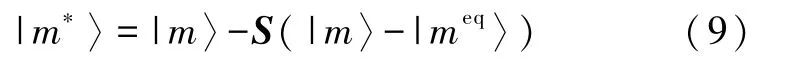
其中|meq〉为Moment空间中的平衡分布函数,S为弛豫过程参数矩阵.在 Moment空间碰撞过程完成后,由转化关系式(8)将分布函数映射回速度空间进行下一步演化.
2 LBM模拟牛顿流体和非牛顿流体泊肃叶流动
2.1牛顿流体泊肃叶流动
流体力学中常把黏性流体在通道中的流动称为泊肃叶流动.首先,我们研究了牛顿流体的泊肃叶流动,当流体沿某方向流动时,恰好使非线性项为零,Navier-Stokes方程化为线性方程而能精确求解.这种情况下,Navier-Stokes方程在直角坐标系下的分量形式是:

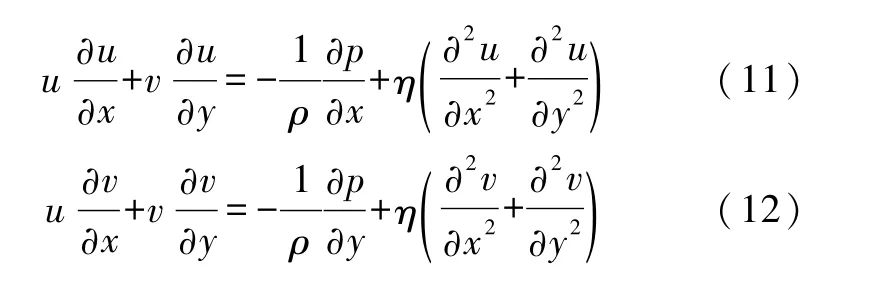
其中u、v分别为速度在x、y方向分量,ρ为流体密度,η为黏度.边界条件和压力梯度为:
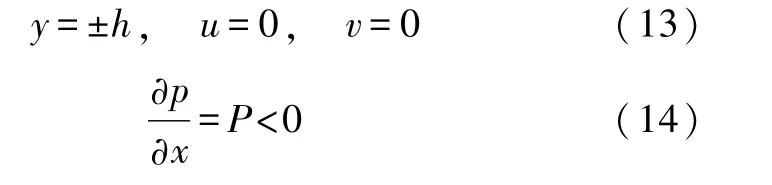
其中h为边界坐标,P为压力常量.
由式(10)—式(14)求解得到 x方向速度分量理论解为
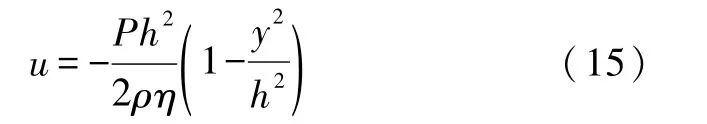
LBM模拟结果可以与理论解进行比较.数值模拟采用二维九速(D2Q9)模型,格子空间尺寸为200×101,流体黏度 η=0.01,上下边界为无滑边界条件,通道入口和出口采用压力边界条件.图1是在垂直流动方向截取得到的x方向速度分量随y轴变化的分布图,模拟给出的x方向速度分量为抛物线分布,模拟结果与理论解完全一致.
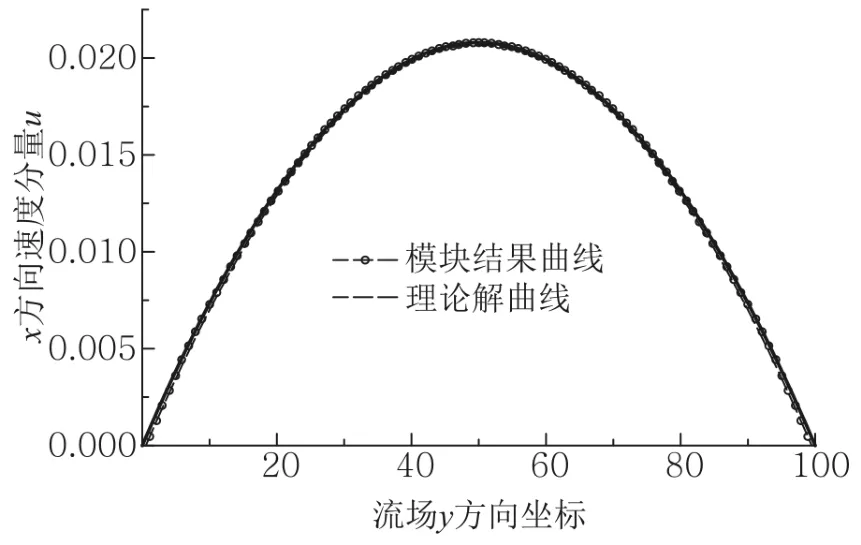
图1 泊肃叶流动中的牛顿流体x方向速度分量的理论解与模拟结果比较
2.2剪切变稀流体泊肃叶流动
非牛顿流体广泛存在于人们的生产生活之中,然而在教学中却经常被忽略.为了培养学生理论与实际相结合的思维方式,有必要对这部分内容进行展开介绍.借助计算机模拟将牛顿流体和非牛顿流体流动现象同时呈现在课堂上,可以帮助学生区别这两类流体.非牛顿流体,是指不满足牛顿黏性实验定律的流体.根据剪切应力与剪切率关系的不同,可将非牛顿型流体分为若干类型,我们以剪切变稀流体为对象进行模拟,并和牛顿流体在通道内的速度分布进行比较.实验表明,大多数高分子溶体和溶液具有剪切变稀性质,其黏度会随着剪切率的增加而减小至无穷黏度 μ∞,即所谓的剪切变稀.用来描述剪切变稀流体的模型有很多种,如幂律模型、Carreau模型和Cross模型[7].我们采用Cross模型:
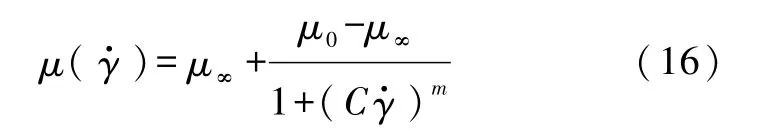
C和m为常数,μ0为零切黏度,μ∞为无穷黏度,为剪切速率.数值模拟采用 MRT D2Q9模型在200×101格子上进行,Cross模型参数为 C=80,m=0.5,μ∞=0.01,μ0=1.
在通道流动中牛顿流体的速度分布为抛物线,而剪切变稀流体在通道中心具有一个速度平台,如图2(a)所示.由剪切变稀流体的黏度与剪切速率的关系可知,在通道中心剪切速率最小黏度最大,从通道中心到两边随着剪切速率的增大黏度逐渐变小,如图2(b)所示.这种黏度与剪切速率的非线性关系不符合牛顿黏性定律,而牛顿流体中黏度不随剪切速率变化.模拟结果很好的体现了牛顿流体和非牛顿流体物理概念上的差异.
3 LBM模拟层流、湍流和卡门涡街现象
层流指流体在管内流动时其质点沿着与管轴平行的方向作平滑直线运动;湍流指相邻流层间不但有滑动,还有混合,流体作不规则运动,有垂直于流管轴线方向的分速度产生.湍流现象普遍存在于地球大气、海洋和江河、火箭尾流及血液流动中的的自然现象.我们选择圆柱绕流问题来演示层流与湍流现象,同时还可以讲解雷诺数 Re的物理意义.在图 3(a)中,当 Re=2.5时,黏性力对流场的影响大于惯性力,流场中流速的扰动会因黏性力衰减,从而维持流体流动稳定,流动为层流;当 Re=164时,惯性力对流场的影响大于黏性力,流速的扰动变化会发展、增强,流动为湍流,如图3(b)所示;当Re=576时,在模拟结果中出现了与实际应用密切相关的卡门涡街现象,物体两侧会周期性地脱落出旋转方向相反、排列规则的双列线涡,如图3(c)所示.
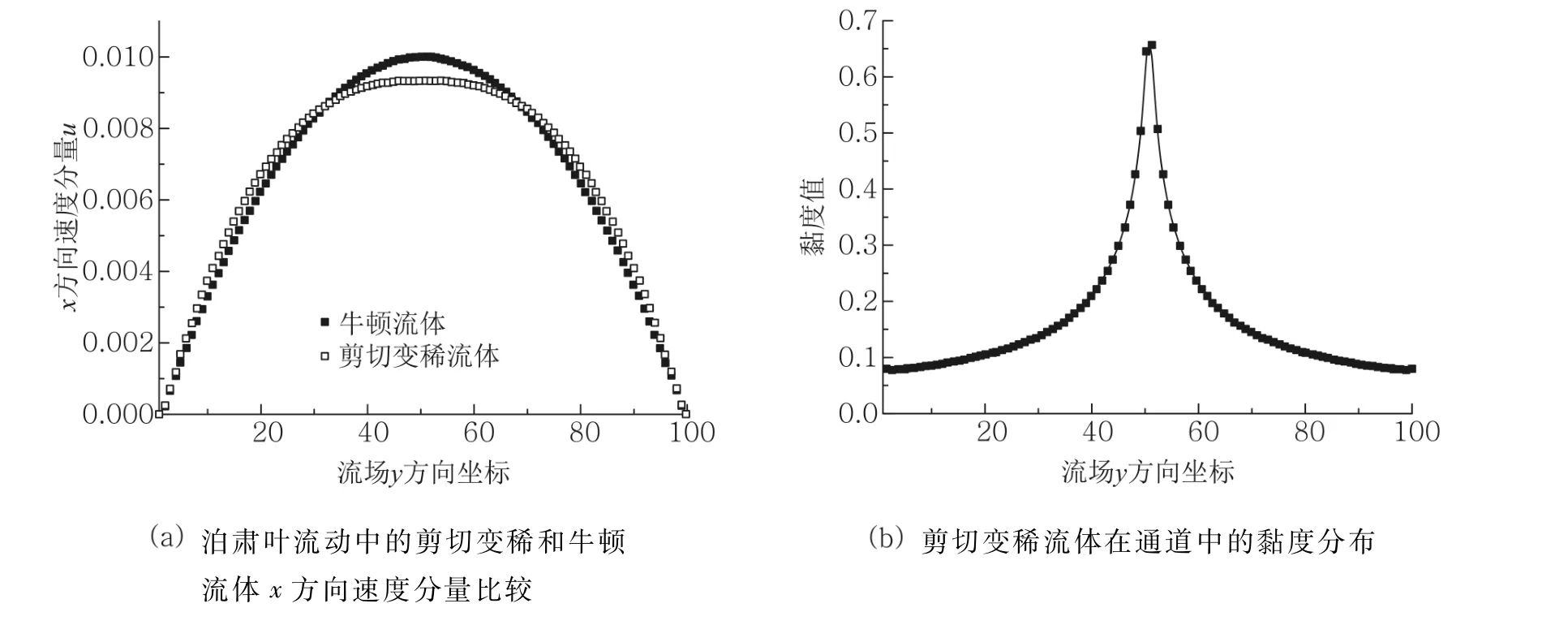
图2

图 3 不同雷诺数条件下,LBM模拟流体层流和湍流现象
4 结论
流体广泛存在于人们的生产生活中,流体力学不仅是物理学重要的基础理论,而且与实际应用密不可分,因此深入学习流体力学知识对理工科学生非常重要.计算机模拟不受时空限制,能够真实还原物理规律,这是其他辅助教学手段不具备的.本文采用计算机模拟作为辅助手段,将模拟结果与大学物理中与流体力学相关的概念和现象相结合,实现提高教学效率,增强教学效果的目的.通过 LBM模拟方法,模拟了牛顿流体和非牛顿流体的泊肃叶流动,发现牛顿流体的泊肃叶流动模拟结果可以与理论解吻合得非常好;通过展示这两类流体在速度分布规律及黏度和剪切速率关系上的差异,形象地阐明了牛顿流体和非牛顿流体的物理概念;最后,模拟了圆柱绕流问题,随着雷诺数的增大可以依次观察到层流现象、湍流现象和卡门涡街现象,在对这些现象进行动态演示和解释的过程中自然阐明了雷诺数的物理意义.这些探索性的工作表明在大学物理课堂上采用计算机模拟做为辅助手段,不仅可以事半功倍,还能够培养学生采用计算物理方法解决实际问题的思维方式.
[1] 韩永胜,杨宏新,马军.Mathematica软件在大学物理问题数值模拟中的应用举例[J].物理通报,2014,(7):31-34.
[2] 丘锡彬,唐昌建.基于计算机模拟技术的现代物理学教学研究[J].高等理科教育,2010,(6):74-77.
[3] 李 钰,康洞国,彭芳麟.刚体绕瞬心的转动方程的计算机模拟[J].大学物理,2003,22(11):44-47.
[4] 熊万杰.Matlab用于大学物理教学[J].物理通报,2004(2):16-19.
[5] 张杰.计算机模拟在分子物理教学中的应用[J].中山大学学报论丛,2005,25(3):31-34.
[6] Pan C,Luo L S,Miller C T.An Evaluation of Lattice Boltzmann Schemes for Porous Medium Flow Simulation[J].Comput Fluids,2006,35:898-909.
[7] Kehrwald D.Lattice Boltzmann Simulation of Shear-Thinning Fluids[J].J Stat Phys,2005,121:223-237.
Computer simulation of some issues on fluid mechanics in college physics
MA Zeng-wei,WANG Zhi-yong,WEI Jian-wei,LIU Gai-qin,HU Nan,LI Rui-feng
(School of Optoelectronic Information,Chongqing University of Technology,Chongqing 400054,China)
Lattice Boltzmann method(LBM)has been widely applied to study some issues on fluid mechanic.In this paper,the Poiseuille flows of Newtonian fluid and non-Newtonian fluid are simulated by LBM.Both laminar flow and turbulent flow are shown in the simulation of flow past cylinder and then the physical concept of Reynolds number is clarified.By combining simulated results with some knowledge of fluid mechanics in college physics,it can not only explain physical concepts on fluid mechanics intuitively,but also guide students to use the method of computation physics to solve problems.
computer simulation;Newtonian fluid;non-Newtonian fluid;laminar flow;turbulent flow
O 351.3
A
1000-0712(2016)10-0017-03
2015-12-16;
2016-04-05
重庆理工大学高等教育教学改革研究项目(2013YB34,2014ZD05)、重庆市教委科学技术研究项目(KJ1400921)、重庆理工大学科研启动基金项目(2012ZD29)资助
马增威(1980—),男,吉林省白城市镇赉县人,重庆理工大学光电信息学院副教授,博士,主要从事大学物理教学及复杂流体的计算机模拟研究工作.
