弹簧静变形和重力加速度从固有频率表达式中消失的条件

陈奎孚，蔡 春

（1．中国农业大学 理学院74＃，北京 100083；2．北京联合大学 应用文理学院，北京 100191）

《对玻恩及其学派的系列研究》连载

弹簧静变形和重力加速度从固有频率表达式中消失的条件

陈奎孚1，蔡 春2

（1．中国农业大学 理学院74＃，北京 100083；2．北京联合大学 应用文理学院，北京 100191）

教学经常使用固有频率表达式不显含弹簧静变形和重力加速度的振子；但也能找到相反的情形．本研究探讨前者的充要条件．分析发现如果弹簧轴线在质点通过静平衡位置时沿其轨迹的切向，则弹簧静变形从固有频率表达式中消失．在满足这一前提下，进一步要求质点轨迹在静平衡位置的曲率为0，或沿铅垂方向，则重力也无回复力的效果，从而重力加速度在固有频率表达式中不出现．该结论不仅有助于理解重力与固有频率之间的关系，也可指导振动例题编制和选用．

振动；弹簧；静变形；势能；固有频率；曲率

弹簧振子是典型的物理教学模型．最简单的情形是图1（a）所示的平放振子（本文只考虑无质量的轻弹簧），稍微复杂一点是图1（b）的竖直悬挂的弹簧振子（仅考虑竖直方向的振动）．后者的一个显著特点是固有频率与重力引起的弹簧静变形无关．同样，图1（c）和图1（d）的两个振子也不用考虑重力引起的弹簧静变形．我们自然会问：是否弹簧振子都不需要考虑重力的影响呢，比如像图2这样的例子（图中m为弹簧振子质量，k为弹簧屈强系数，δst为弹簧的静伸缩量）？答案是否定的，笔者已经给出了反例［1，2］，如图2（a）所示的振子.

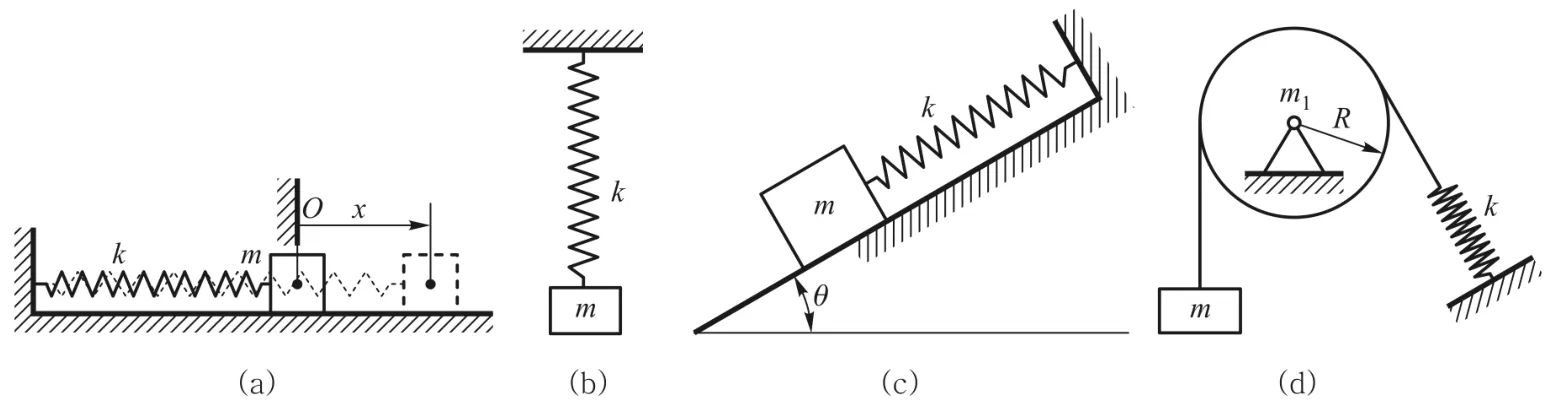
图1　固有频率表达式中不显含弹簧静变形的振子

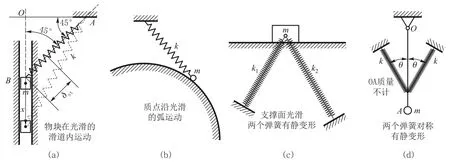
图2　固有频率表达式涉及弹簧静变形的振子

在很多工程场合，弹簧都有维持静平衡的静变形，但即使像机械振动、结构动力学这些专业课程教材也没有就弹簧静变形和重力加速度影响给出很确切的说法［3，4］，更遑论大学物理教材.在这些课程教学中，经常使用图1这组例题（m是弹簧振子质量，k是弹簧倔强系数）.这组特例，如果没有特别的提醒，当然会导致学生误认为固有频率总与弹簧静变形无关.一方面我们需要提醒学生以避免这种错误的认识，另一方面为了与图1这样例题的衔接，我们需要知道在什么样条件下，静变形和重力加速度不会出现在固有频率表达式中.明确了这个条件，一方面能加深对工程场合中静变形作用的认识，另一方面也可有效地避免编制新习题和例题的不当或错误.

1 弹簧静变形消失的条件

我们只讨论无阻尼情形.教学中广泛使用无阻尼振子，这是因为，一方面它是研究有阻尼振子的基础，另一方面就工程分析最感兴趣的目标参数固有频率而言，阻尼固有频率和无阻尼固有频率差异不大（大部分工程结构的阻尼都很小）.

无阻尼振子的运动规律完全被势能和动能两个能量所确定.

先考虑广义坐标.除了某些极个别情形外［5］，广义坐标几乎是可以任意选择的.我们这里选择从平衡位置出发沿质点轨迹的弧坐标s为广义坐标.采用此种做法，质点m的动能表达式为Ek=，肯定不含静变形 δst.接下来只需研究势能即可.

图3是振子示意图，先考虑其在光滑的水平面内运动（即暂不考虑重力的影响）.不失一般性，研究其中一条弹簧AB的势能.弹簧AB一端固定在A点，另一端连在质点m上.质点m被约束在固定的光滑约束曲线 L上运动.图中符号：l代表自然长度；δst代表弹簧的静伸缩量（静变形）.运动中质点从静平衡位置B移动到C，其弦长记为λ.

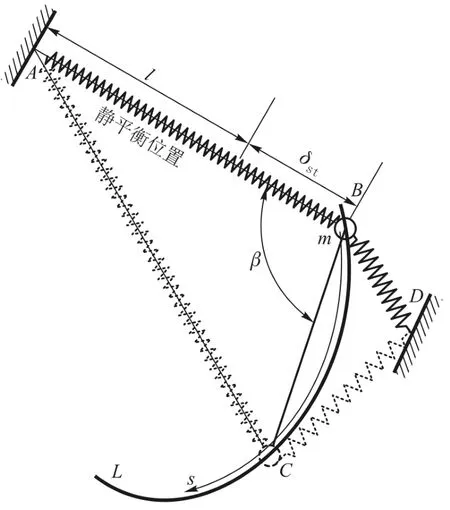
图3　振动中的弹簧

利用余弦定理有

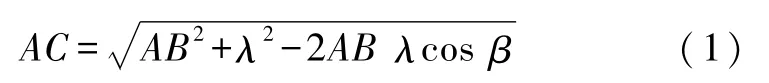
选定弧坐标s为广义坐标后，所有与振子相关的变量都可以表示为s的单变量函数，如AC、λ、β都是s的函数 AC（s）、λ（s）、β（s）.先看 BC（s），对于微幅线性振动，只需关心到它的泰勒级数的s2即可，即

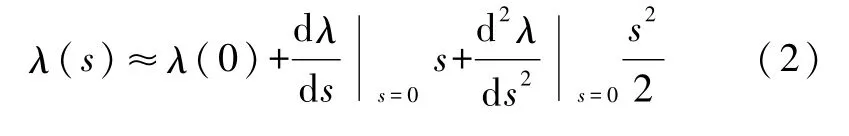
在式（2）中，因静平衡位置对应s=0而有

为了做进一步的运算，我们对“弧长的导数”的内容放到第4节里，由第4节的式（23）和式（24）可得

将β（s）也展开到泰勒级数的s2，得

把式（4）和式（5）代入式（1），并且也保留到s2有

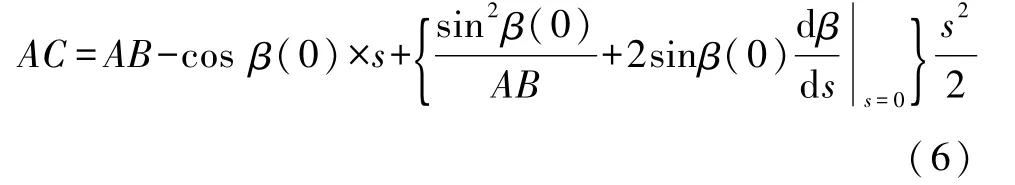
下面利用式（6）分析势能.选择静平衡状态为此弹簧的势能零点，则弹性势能为（需指出：弹性势能Ep的二次项与的不同，不可简单套用）

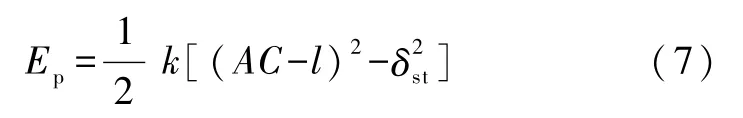
将式（6）代入式（7）并保留到s2有

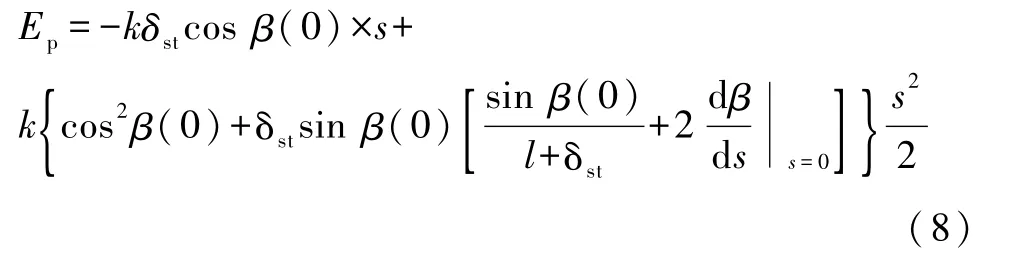
选择静平衡位置为坐标原点，式（8）右边第一项会被其他势能（比如其他弹簧或重力等有势力）抵消.对固有频率有实质影响的是式（8）右边第二项.

l和δst是静变形弹簧的两个独立参数，要使它们从式（8）右边的第二项中消失，当且仅当

几何上，这就要求当质点过静平衡位置时，弹簧轴线与B端（质点）轨迹相切，或者说振子偏离静平衡位置所导致的弹簧伸缩是主导的，而弹簧在运动平面内的转动是可忽略的更高阶微幅量.

综上所述：弹簧静变形从振子固有频率表达式中消失的充要条件是弹簧轴线与质点轨迹在静平衡位置处相切.

显然图1（b）、1（c）和1（d）满足上述条件，故而固有频率表达式不显含弹簧静变形．然而，对图2（a）、图 2（c）（θ≠90°）、图 2（d）的3个振子，因弹簧轴线与质点的运动轨迹在静平衡位置不相切，所以固有频率表达式必然出现弹簧的静变形．对图2（b）的振子，若系统参数很巧，使得弹簧轴线在静平衡位置与固定圆弧相切，则固有频率表达式不含弹簧静变形．

2 重力加速度消失的条件

重力有两个独立的效果，第一个效果是决定静平衡位置，第二个效果是作为回复力的一部分．重力第一个效果引起了弹簧静变形，其消失条件就是上节的结论：要求弹簧轴线与质点运动轨迹相切于平衡位置处．

重力的第二个效果是成为回复力的一部分．如果质点发生直线运动，比如图1的4个例子，重力都没有回复的效果．然而对单摆，重力则是该振子的前提，因为重力沿摆锤轨迹切线的分量构成单摆的回复力．

下面讨论重力无回复力效果的条件．

重力势能Epg=mgy，其中y是振动过程中质点离平衡位置的垂直高度.同样以平衡位置为原点，沿质点轨迹的弧坐标s为广义坐标.对于微幅线性振动，对固有频率有贡献的是势能对s的泰勒展开式的s2项，其系数为（mg/2）（d2y/ds2）.因此重力对固有频率没有贡献的充要条件是：在平衡位置有

对弧长导数的几何意义很难理解，因此我们把式（10）换成对直角坐标的导数.

图4的虚线是振子质点的约束曲线，设标注字母处为质点的静平衡位置.这组静平衡位置可分为两类.第一类是A类，过该点的轨迹切线与x轴不垂直，如图中的A、A1、A2、A3各点.第二类是B类，过该点的轨迹切线与x轴垂直，如图中的B、B1、B2、B3各点.

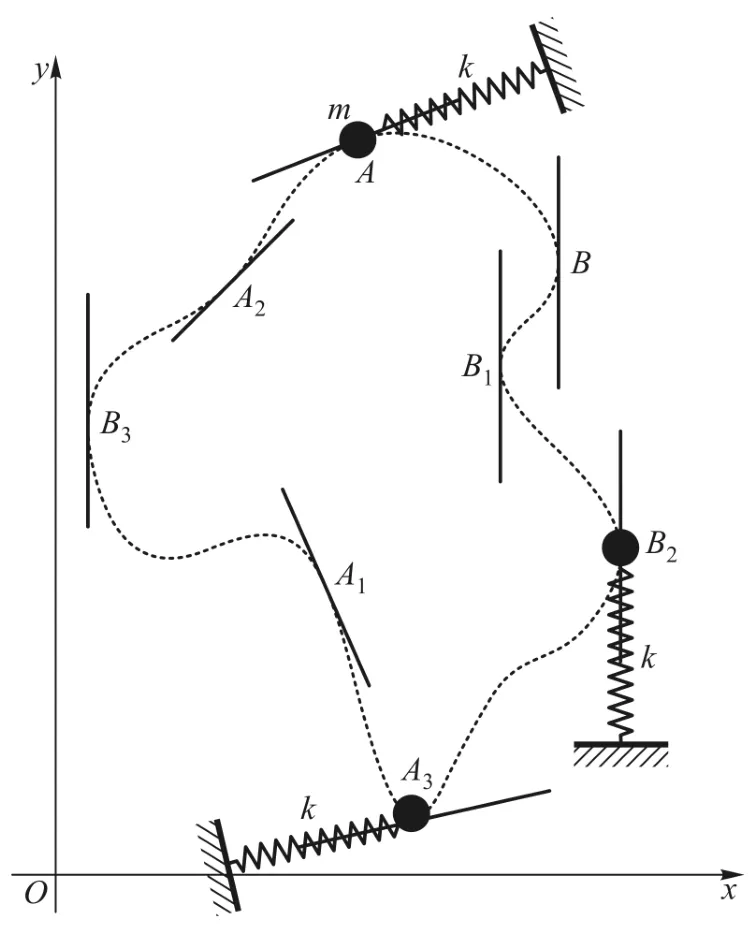
图4　静平衡位置分类

在A类平衡位置的邻域，轨迹可以表示成函数y（x）.条件式（10）可以转化成（见4节式（17））

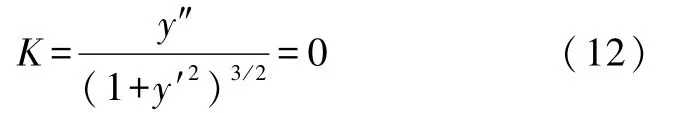
当然式（12）几何意义也可以说成是：平衡位置处的质点轨迹曲率半径为无穷大.常见 y=tan x，y=sin x在x=0处就是这样的情形，它们 x=0处斜率为1，但是曲率半径为无穷大.

任何一条光滑曲线，当曲线弧段比较短时都接近直线.再进一步，在曲率为0处，弧段接近直线的程度更高.在相同的近似精度下，在曲率为 0的附近，曲线能用一条直线近似的范围要比其他地方长得多.因此曲率为0的平衡位置将更接近图1的振子情形.

如果y′在平衡位置两侧改变符号，则式（11）的y″=0就变成了拐点条件.图5是刻意构造的弹簧振子，质点 m限制在曲线轨迹 y（x）=x3-6x2-7x+60上运动.调整振子参数，使其平衡位置为（2，30），且弹簧轴线在该点与曲线相切.因为曲线 y（x）在（2，30）处曲率为0，故重力加速度不会在这个振子的固有频率表达式中出现.图5这样的振子在教材中几乎不会出现，但是一个科学结论则应覆盖尽可能大的范围.对图2（b）的振子，因固定圆弧的曲率不为零，即使弹簧轴线与固定圆弧相切，其固有频率表达式仍含有重力加速度.

图5　固有频率不显含重力加速度的振子

如果y″≡0，轨迹就变成了直线，这就是图1（c）的情形.

该散热器主体尺寸为：520×445×220mm，风扇转速为2 000r/min，仿真分析液压模型，系统最终平衡时油箱温度为71℃。此时散热器的冷却功率为8.6kW(图11)。

在B类平衡位置附近，轨迹可以表示成函数x（y）.式（10）条件可变为（见4节式（18））

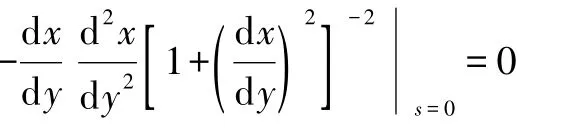
综上所述，在平衡位置处，如果质点的轨迹沿垂直方向，或者轨迹曲率为零，则重力加速度会从微幅振动的固有频率表达式中消失．除此之外，都必须考虑重力的贡献．

4 对弧长的导数

在第2节和第3节中使用了对弧长导数的若干结果．就笔者所接触的资料，未见对弧长导数的系统介绍和演绎，因而在本节给出相应的论证过程．

4．1坐标对弧长的导数

弧长微元和坐标微元的关系为

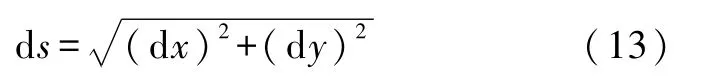
因此当x（s）和y（x）的两个函数存在时

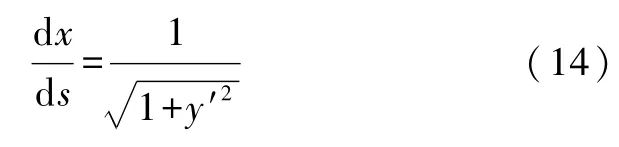
其中y′=dy/dx.

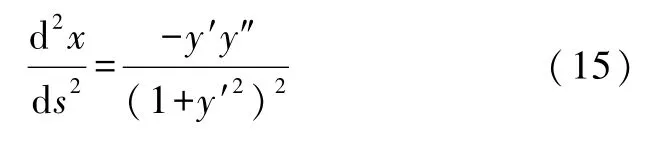
当y（s）函数存在时

式（16）再次对s求导有

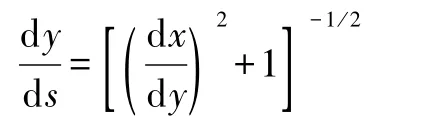
对s再次求导有

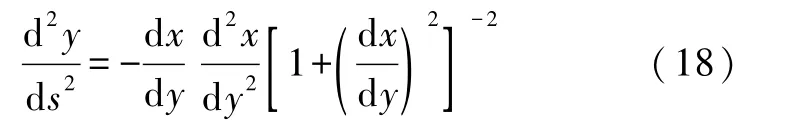
4．2弦对弧坐标的导数

设图3中B和C的两个点坐标分别为（xB，yB）和（x，y）.由勾股定理有

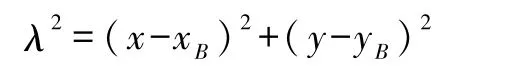
两边对弧长l求导得到（约去因数2）

将式（14）和（16）代入可得

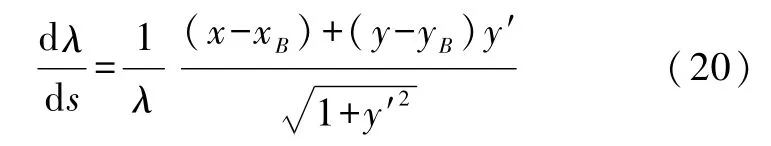
式（19）再次对s求导有

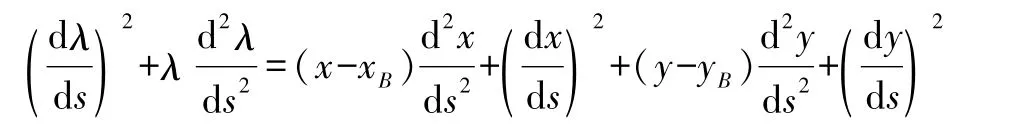
解得

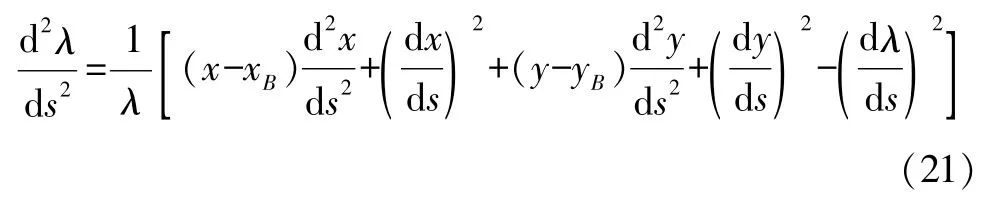
将式（14）—式（17）和式（20）代入式（21）得到

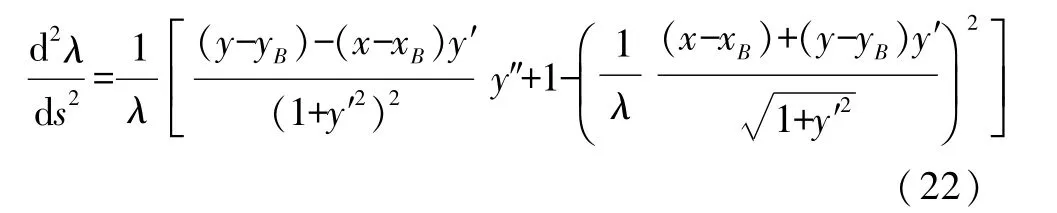
再来考察C点趋近于B点的情形.显然式（20）和式（21）中y′和y″是C点的导数.为了便于分析，可认为C点不动，而B点趋近于C点.记Δx=x-xB，Δy=y-xB.因为轨迹一般都是光滑的（y″是有界的），所以有

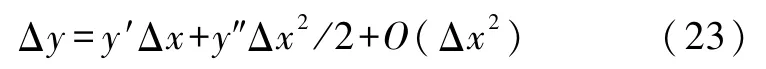
代入式（20）有

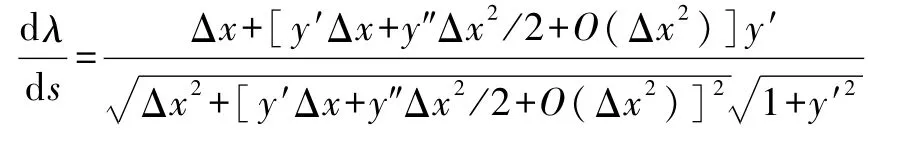
展开到Δx二次项有

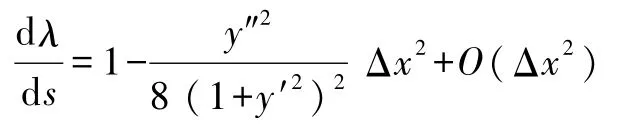
显然当s趋近于0，有

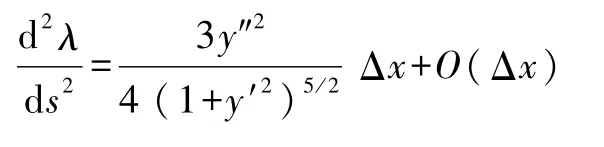
因而有

4 结束语

本文研究了两个有关联的问题，一是弹簧静变形从固有频率表达式中消失的条件.理论分析导出该条件为弹簧轴线与质点轨迹在静平衡位置处相切.另一个问题是，重力加速度在什么样条件下不出现在固有频率表达式中.

重力对振子固有频率有两个效果，一是决定静平衡位置，从而导致弹簧有静变形.为了消除弹簧静变形对振子频率的影响，进而消除重力对振子频率的影响，则要求质点过静平衡位置时，弹簧轴线与质点轨迹相切.重力的第二个效果是回复力.为了让重力没有回复力效果，则质点轨迹在平衡位置处曲率为零或沿竖直方向.

此外，笔者还推导了坐标和弦长对弧长的导数.这是采用弧坐标分析的数学基础.

本文只考虑了质点振动情形，对含有刚体的振动系统还需要进一步的研究.

［1］ 陈奎孚，蔡春．关于“对物理教材中两个概念的讨论”中“加减平衡力系”的商榷［J］．物理与工程，2015，25（1）：59-60．

［2］ 陈奎孚，蔡春．仅据平衡位置为系统弹性势能零点就能使振子势能为 kx2／2吗？［J］．物理与工程，2015，25（2）：52-54．

［3］ 陈奎孚．机械振动教程［M］．北京：中国农业大学出版社，2014．

［4］ 于开平．结构动力学［M］．3版．哈尔滨：哈尔滨工业大学出版社，2015．

［5］ 薛纭．虚功原理与广义坐标［J］．大学物理，2002，21（4）：3-5．

The sufficient conditions for the spring’s static deformation and gravity acceleration vanishing from the intrinsic frequency expression of a vibrator

CHEN Kui-fu1，CAI Chun2
（1．College of Science，China Agricultural University，Beijing 100083，China；2．College of Arts and Science，Beijing Union University，Beijing 100191，China）

Vibration teaching practice employs a plenty of such kind of examples with the gravity and spring’s static deformation not contributing to intrinsic frequencies．However，there exist indeed counter examples with the gravity and spring’s static deformation playing a role．We investigate the if-and-only-if conditions for the spring’s static deformation and gravity acceleration vanishing from the intrinsic frequency expression．Theoretical analysis shows that the spring’s static deformation vanishes from the intrinsic frequency expression if the spring axis is tangential to the particle trajectory at the static balance position．With this condition satisfied，the gravity acceleration vanishes from the intrinsic frequency expression if the particle trajectory transgressing the static balance position is either vertical or zero curvature．The conclusion is not only benefit to comprehend the significance of the gravity to the intrinsic frequency，but also useful in compiling and creating new examples for vibration teaching practice．

vibration；spring；static deflection；potential energy；intrinsic frequency；curvature

O 321；O 302；TB 123

A

1000-0712（2016）10-0023-05

2015-08-06；

2016-03-03

北京市属高等学校高层次人才引进与培养计划项目（CIT＆TCD201404080）资助

陈奎孚（1969—），男，江苏泗洪人，中国农业大学教授，主要从事力学、振动的教学和研究工作．

蔡春，E-mail：caichun＠buu．edu．cn