引力波与广义相对论
2016-12-12刘文彪张轩中
赵 峥,刘文彪,张轩中
(1.北京师范大学 物理学系,北京 100875;2.北京市科学技术协会 蝌蚪五线谱网,北京 100101)
引力波与广义相对论
赵 峥1,刘文彪1,张轩中2
(1.北京师范大学 物理学系,北京 100875;2.北京市科学技术协会 蝌蚪五线谱网,北京 100101)
介绍了引力波的广义相对论理论基础.介绍如何通过双星周期的时间改变间接检测引力辐射,如何利用引力波的偏振效应直接检测引力波.
引力波;广义相对论;双星;偏振;LIGO
今年2月11日,美国国家科学基金会宣布:人类首次探测到了引力波.并宣称,这次探测到的引力波来自13亿年前的2个黑洞的碰撞.这一爆炸性新闻在社会上引起了巨大反响,“引力波”与“黑洞”2个耀眼的名词同时跃入了广大读者的眼帘[1].
这次探测到的引力波事件,实际发生在2015年9月14日(因此标记为 GW150914).有关研究团队出于谨慎,对观测数据进行了反复推敲,直到确认无误后,才予以公布,所以发表时间推迟了近5个月.因此可以认为,他们的发现可信度很高,大多数科学家均对这一发现予以了正面肯定.
引力波的发现是科学史上的一件大事,是对爱因斯坦广义相对论的又一重大验证.近来,报道这一发现的文章很多,但一般都不介绍产生和探测引力波的基本原理.这篇文章将向具备大学物理知识的教师、学生和一般读者简单介绍引力波的理论基础和现有探测手段的基本原理[2-5].
1 引力场以光速传播
1915年,爱因斯坦发表了广义相对论,这一理论既可以看作他的狭义相对论的发展,也可以看作牛顿万有引力定律的发展.
广义相对论认为,万有引力不同于电磁力等人们熟悉的力,本质上是一种几何效应,是时空弯曲的表现.
在牛顿理论中,万有引力是瞬时传播的,从一点传播到另一点不需要时间,也就是说引力的传播速度可视为无穷大.
在爱因斯坦的广义相对论中,时空弯曲情况(即万有引力)的传播速度不是无穷大,而是与光速相同.
广义相对论的基本方程是爱因斯坦场方程[2-7]:
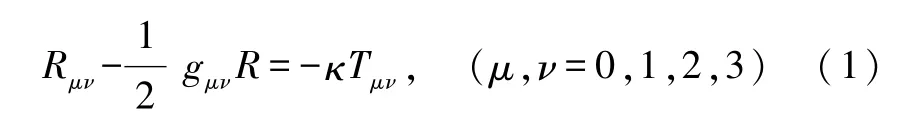
方程的左边表示时空弯曲的情况,是几何量;其中gμν是度规张量,可以简单理解为万有引力定律中的引力势;但引力势一般只有1个分量,而gμν有16个分量(当μ、ν分别取0,1,2,3时.其中0对应时间坐标;1、2、3对应空间坐标),不过由于对称性(gμν=gνμ),其中只有10个分量独立,所以度规张量所含信息量要多于通常所说的“引力势”;Rμν和 R分别为里奇张量和曲率标量,它们是由度规及其一阶导数和二阶导数组成的非线性函数.方程的右边是物质项,Tμν是能量动量张量,由物质的能量、动量、能流和动量流组成.式中常数

其中G是万有引力常数,c是真空中的光速.
场方程(1)告诉我们:物质的存在和运动如何决定时空的弯曲.人们求解场方程,就是要解出满足方程(1)的度规张量 gμν,知道度规张量就可以算出时空的曲率,从而了解时空弯曲的情况.
考虑到式中张量的对称性(Rμν=Rνμ,gμν=gνμ,Tμν=Tνμ),场方程(1)是由10个二阶非线性偏微分方程组成的方程组.遗憾的是,这10个方程中含有4个恒等式,独立的方程只剩6个.6个方程无法决定10个未知函数gμν,于是人们引进所谓“坐标条件”.由4个方程组成的坐标条件,从物理上讲就是选择坐标系.加上坐标条件后,我们就有了10个方程,待求解的函数也是10个,正好自洽,这一点与电磁学类似.用电磁四矢Aμ表述的麦克斯韦方程组中含有一个恒等式,因而要引进规范条件,例如洛伦兹规范或库仑规范.加上规范条件后就得到了4个方程,用4个方程恰好可以解出4个电磁四矢的分量.所以,广义相对论中的“坐标条件”也可以视为规范条件[2-4].
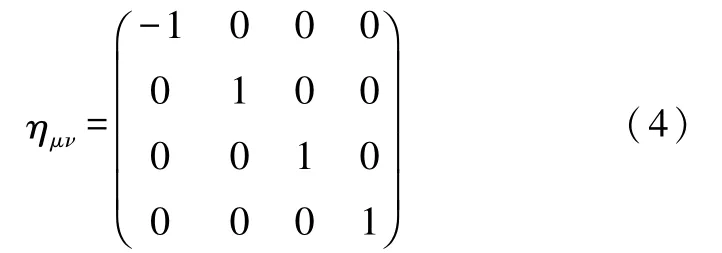
场方程的非线性耦合很强,很少能求出严格解.研究者往往采用近似方法求解,其中一种线性近似方法常可以在引力场较弱的情况下使用.这种方法是,在时空弯曲得不太厉害的情况下,可以假想度规张量偏离平直的闵可夫斯基度规很小,gμν可写成

其中ημν是平直的闵可夫斯基度规:
偏离平直情况的函数hμν很小,即
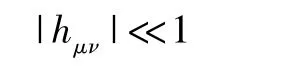
在广义相对论中,经常采用福克建议的谐和坐标条件,这个条件决定的时空坐标满足调和方程.谐和坐标条件的优点是,在引力场趋于零时,可以自动回到平直时空的惯性坐标系.
可以证明,在弱场线性近似式(3)和谐和坐标条件下,场方程(1)可化为

其中,□为达朗贝尔算符,
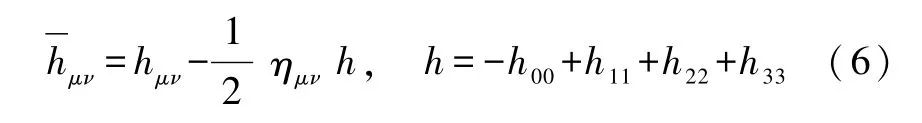
方程(5)的解为
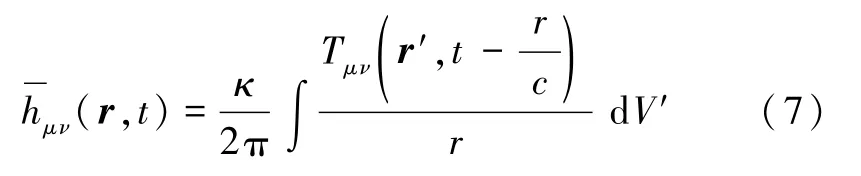
值得注意的是,这是一个推迟解.它表明,t时刻空间r处的引力场,由此前时刻位于′处的源决定.这就是说,物质源的变化所造成的引力场的变化,不是瞬时传播的,而是以光速传播的.这种情况与平直时空的电磁场情况类似.在电动力学中,我们知道,在洛伦兹规范下麦克斯韦电磁四矢方程可写为
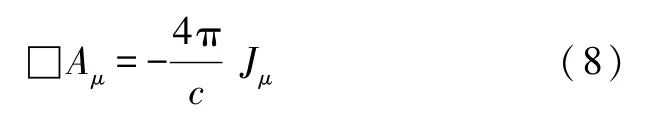
方程(8)的解恰是我们熟悉的电磁势的推迟解:
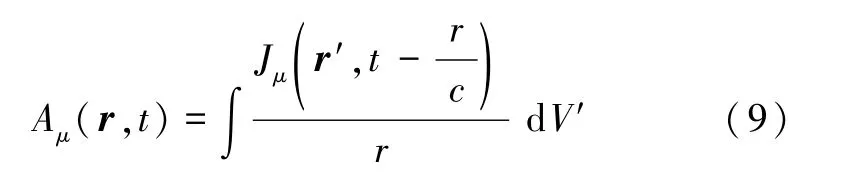
它表明电磁场是以光速传播的.
2 对引力波的预言和讨论
既然引力场本质上是时空弯曲效应,这种效应又以光速传播,那么引力源运动、变化所造成的时空弯曲改变也一定会以光速传向远方,这就是引力波.爱因斯坦在发表广义相对论的第2年(1916年),就预言了引力波的存在.
不过,很快就弄清楚了:不存在球对称的引力波,这是因为发现了一条定理——伯克霍夫定理.它告诉我们,当球对称引力源的外部是真空的时候,如果引力源在变化过程中保持严格的球对称,例如球对称的膨胀、收缩或脉动(即胀缩交替),则外部时空弯曲的情况将不会随时间变化,也就是说外部时空会一直保持静态,不会有引力波发出.
对于是否存在非球对称引力波的探讨,也是一波三折.1936年,在研究平面引力波时,爱因斯坦曾一度误以为不存在引力波,后经审稿人指出错误后,又改而认为存在柱对称的引力波[8].
考虑到地球附近不存在足够强的、易于观测到的引力波,一般认为人类可能探测到引力波的波源都距离我们十分遥远.因此,不管这些引力波的波源具有什么对称性,诞生时引力波的对称性如何,强度多大,来到我们附近的引力波都可以近似看作强度很弱的平面波.
下面我们就以平面波为例,来说明引力波的性质.我们用与电磁波做比较的方式来进行讨论.
当电流源Jμ为零时,方程(8)化为波动方程.它表明电磁场以波动的方式传播,传播速度为光速.同样,当物质源Tμν为零时,方程(5)也化成波动方程,这说明引力场与电磁场类似,也以波动方式传播,引力波的传播速度也是光速[2-5].
不难看出,电磁波有2个独立的极化矢量,且都与波矢垂直,所以电磁波是有两种独立极化方式的横波.研究表明,引力波也只有2种独立极化方式,而且极化方向也都与引力波的波矢方向垂直.所以,引力波也是有2种独立极化方式的横波.
量子电动力学告诉我们,光量子是静质量为零、自旋为1的粒子.引力场量子化的研究也告诉我们,如果有引力子的话,它也应该是静质量为零(“静质量为零”与“传播速度为光速”是互为因果的)的粒子,但它不是自旋为1的矢量粒子,而是自旋为2的张量粒子.
需要说明的是,迄今为止,引力场量子化的企图一直未能成功,研究遇到很大困难,这是一个目前正在探讨的课题.比较有希望获得突破的是“超弦”和“圈量子引力”2种方案,感兴趣的读者可参看有关书籍和文献.
人类目前对引力波的实验探测,是把它作为连续的经典波来对待的,还没有考虑引力波量子化后的性质.
3 引力波的偏振效应
广义相对论认为,弯曲时空中的自由质点(即不受引力之外任何力作用的质点),将作惯性运动.弯曲时空中没有直线,但有直线在弯曲时空中的推广——测地线.自由质点和自由光线就沿测地线作惯性运动.在广义相对论采用的黎曼几何中,测地线就是短程线.它是在四维时空中长度取极值的线,但不一定是最短线,还可能是最长线.实际上,对于质点,短程线恰是2点间的最长线,而不是最短线,这是不熟悉广义相对论的人容易误解的事情.
爱因斯坦建立广义相对论时,认为他的理论有2个基本方程,一个就是前面说到的场方程(1),它表明“物质告诉时空如何弯曲”.另一个是运动方程,即测地线方程:
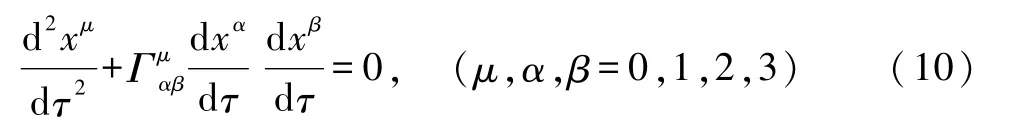
它表明“时空告诉物质如何运动”.式中,τ为固有时,即质点自己“经历”的真实时间.叫做联络,它由度规及其一阶导数构成,相当于牛顿引力论中的“引力场强”.式(10)中,重复的上下指标代表从 0到3求和,这是爱因斯坦提出的“惯例”,也是他对数学做出的一点小贡献:此规定省略了求和符号,使方程更加简洁.
后来的研究表明,从场方程可以推出运动方程,因此,广义相对论的基本方程归根结底只有一个,那就是场方程.
一些人研究了2个相邻的自由质点在弯曲时空中沿测地线运动时,质点间的距离如何变化.他们得到了测地偏离方程[2-4]:
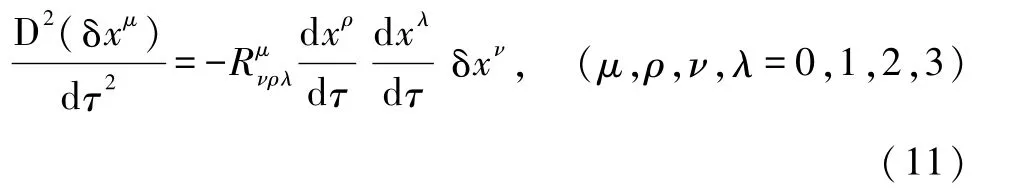
此式给出了2个自由质点间的相对加速度.注意,这是引力场产生的特别的潮汐效应,纯粹的惯性力场无此效应.这是因为“相对加速度”起源于非零的时空曲率,而平直时空中的曲率张量肯定为零.
作为广义相对论基础的等效原理告诉我们,引力场与惯性场等效:在时空一点的邻域,任何物理效应都无法区分引力场与惯性场.但要注意,“等效”仅限于时空一点的邻域,如果考虑2个以上的时空点,引力场与惯性场肯定可以区分.2个自由质点间的相对距离是否发生变化,就是区分引力场与惯性场的方法之一.所以,等效原理是一个局域性原理.
现在我们把测地偏离方程应用于平面引力波的研究.
首先让我们来看一组瞬时相对静止的自由质点(例如都在引力场中自由下落),它们的相对速度为零,即
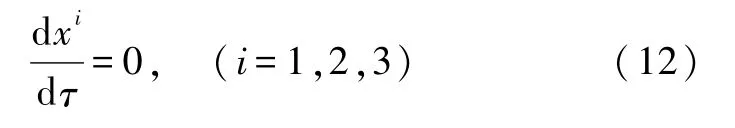
从式(11)不难看出,这时质点间的相对加速度为
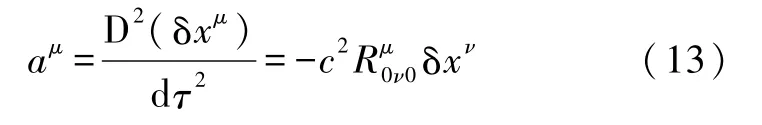
或
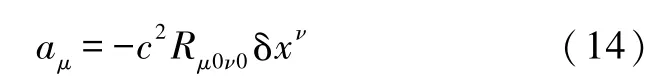
考虑沿x3轴运动的平面引力波,它的波面处在垂直于x3轴的x1x2平面内.设在此平面内有一组相对瞬时静止且排成圆圈的自由质点,还有一位处于圆心的自由下落观测者,观测者到各点的距离用坐标差δx1和δx2来描述.
在式(3)所示的弱场线性近似下,按照曲率张量的定义,不难算出不为零的、独立的曲率张量分量仅剩下2个:
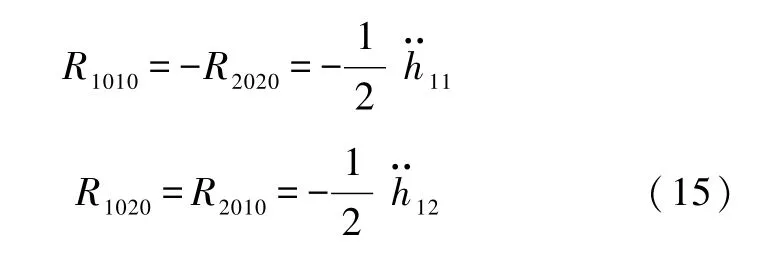
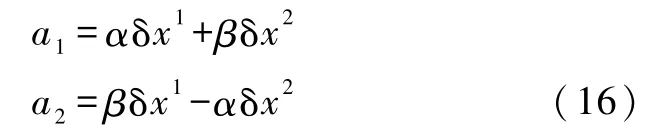
式中
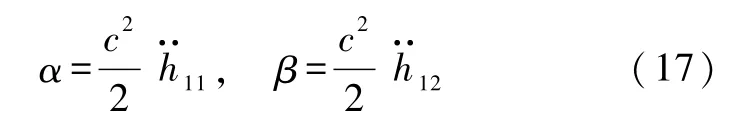
式(16)写成矩阵形式为
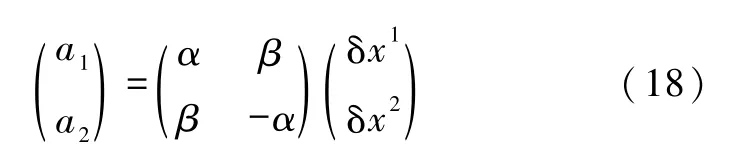
上述相对加速度是引力波的极化(偏振)效应(四极共振)产生的,是引力波造成的一种潮汐效应.研究表明,引力波的偏振有2种类型,一般用⊕和⊗来标记.
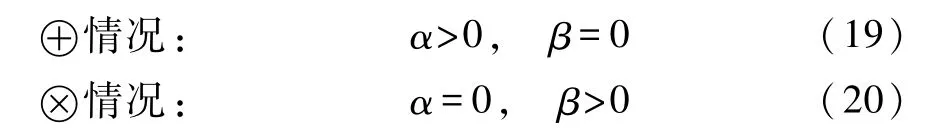
即分别决定于h11和h12随时间的变化.
表1和表2给出了上述2种情况下算出的圆周上各点的相对加速度.图1和图2画出了圆周上各自由质点相对加速度的方向,及圆周的形变趋势[4].

表1 ⊕型偏振,即α>0,

表2 ⊗型偏振,即α=0,
图1中位于正圆周上的自由质点,在引力波四极共振下,先是变成左右拉伸、上下压缩的椭圆,然后退回正圆,再形成上下拉伸、左右压缩的椭圆,……,这样反复交替.图2中的正圆,也是反复拉伸压缩,两种正交的椭圆不断交替.显然,这是一种引力波偏振产生的潮汐加速度所特有的“剪切效应”.
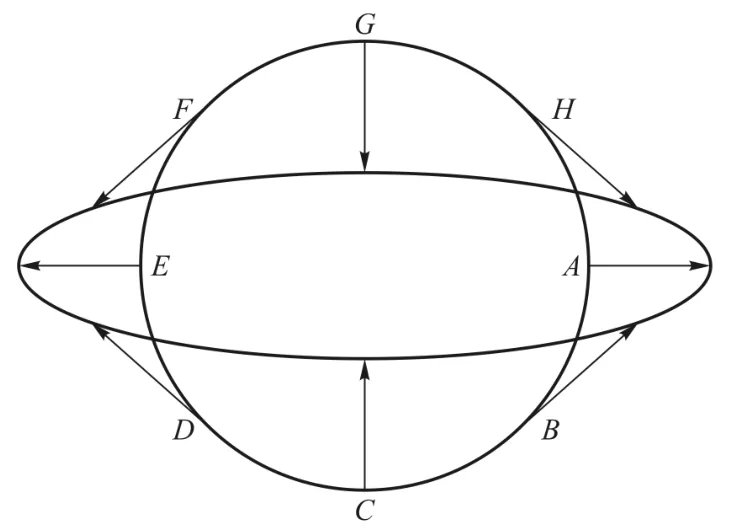
图1 ⊕型偏振,即α>0,

图2 ⊗型偏振,即 α=0,β>0
4 引力辐射能的计算
现在我们来介绍引力源对引力能的辐射,也就是计算引力波从辐射源带走的能量[2,3].
推迟解式(7)可简写为
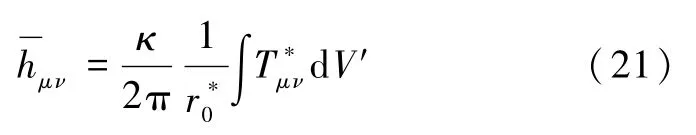
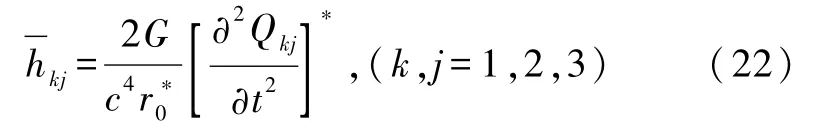
式中

为引力源物质的质量四极矩,μ为静质量密度.
式(22)可改写为
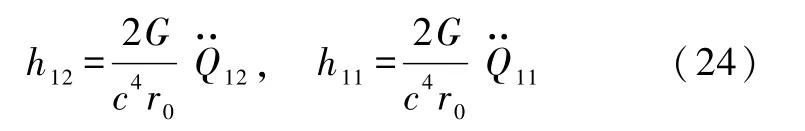
这是在弱场近似下得到的结果.式(24)表明引力波辐射按多极辐射展开时,最低阶为四极辐射,偶极辐射没有贡献.实际上,偶极矩部分是决定场源质心位置r0的,.由于孤立系统的质心作匀速运动,所以不存在偶极辐射.我们知道,电磁系统是以偶极辐射为主的,四极辐射比偶极辐射弱得多.引力源只产生四极辐射,没有偶极辐射,所以引力波远弱于电磁波,探测起来十分困难.
研究引力辐射的另一个重要困难是“能量表述”问题.爱因斯坦等人早就发现,引力能与电磁能不同,引力场能量的密度不是张量,依赖于坐标系的选择.在反复推敲之后,爱因斯坦和托曼提出了一个引力能的表达式,称之为引力能的爱因斯坦-托曼表述.此表述提出后,苏联的朗道和栗弗席兹指出这种表述存在严重缺陷.他们又提出了一个新表述,朗道-栗弗席兹表述.但过了不久,有人指出朗道表述也有缺点,又提出新的表述.然而,不管哪一种表述,都存在严重缺点.人们终于认识到,引力场的能量密度不可能严格定义,只能定义所谓的准局域能.不过,人们又发现,以前提出的那些“能量表述”虽然有缺点,但在计算引力辐射时都还可以使用.
各种能量表述的表达式均十分复杂.例如,纯引力场能量-动量的朗道-栗弗席兹表述为[2,3,6]
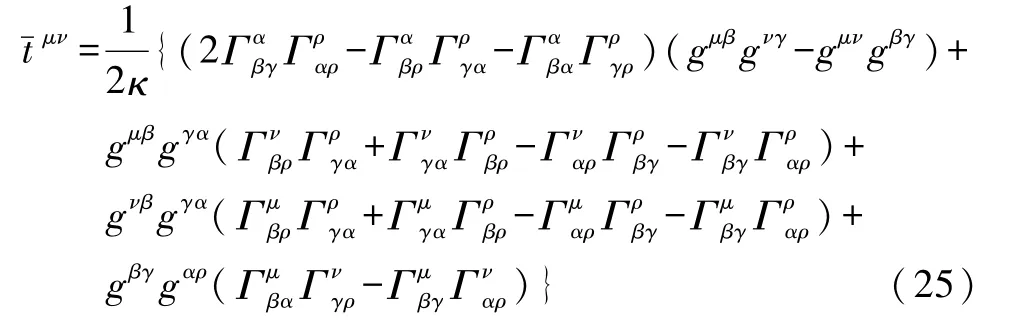
采用朗道-栗弗席兹表述后,经过繁复的计算,可得到平面引力波的能流密度为
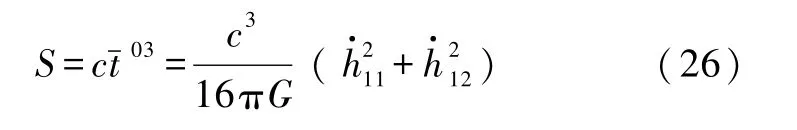
或用四极矩的变化表出
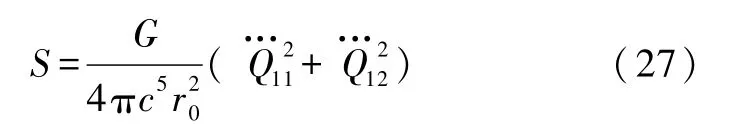
可见,引力辐射的能流密度决定于引力源质量四极矩对时间的三阶导数.
进一步的计算表明,由于引力辐射,引力源能量的减少可用下式给出
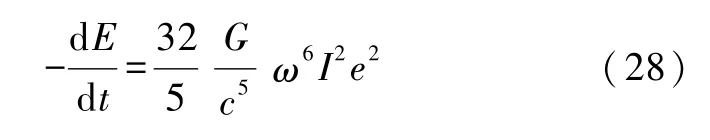
式中ω为引力源的转动角速度,而

为在随动坐标系中算出的引力源绕x3轴(即引力波前进方向)的转动惯量,而

为赤道椭率.用式(28)可以算出引力源辐射引力波的功率,下面举几个例子.
例1 回转对称球.
例2 以半径为r的圆周作公转的质点m.
由于I=I1=mr2,I2=0,e=1,有
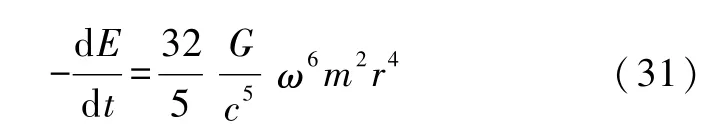
假设木星(太阳系中最大的行星)的绕日转动可看作上述圆周运动.由于木星公转角速度为ω=1.68×10-8s-1,木星的质量为 m=1.9×1030g,公转轨道平均半径为 r=7.78×1013cm,可算出木星引力辐射的放能率为
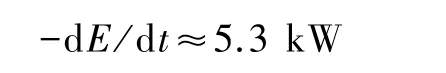
相当于一个电灯泡射出的能量.所以,太阳系中行星运动产生的引力辐射完全可以忽略不计.
例3 中子星自转.
设一颗质量 m=1M⊙(M⊙为太阳质量),半径r=10 km,转动惯量I=1.0×1045g·cm2,自旋角速度为ω=1.0×104s-1的中子星,可算出
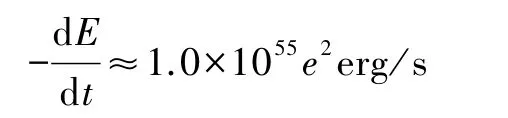
中子星自转动能为 1.0×1053erg,只要 e不小于1.0×10-4,中子星的自转动能就会在几年内辐射掉.但由于辐射阻尼的影响,转速会迅速降低,辐射放能率也就会迅速减小.不过,中子星在形成初期,引力辐射应该十分重要.
例4 双星.
先看圆运动情况.设双星运动可近似看作其中一颗以折合质量围绕另一颗作圆周转动.根据开普勒第三定律
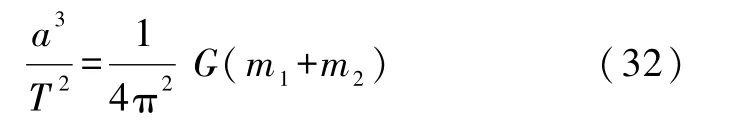
可知转动角速度
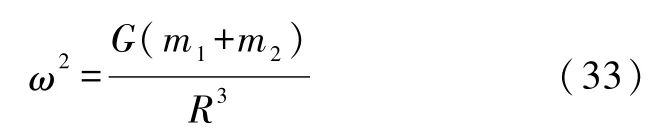
R为2颗星的距离,转动惯量为

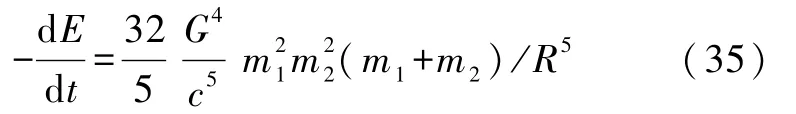
如果轨道是椭圆,研究表明放能率为
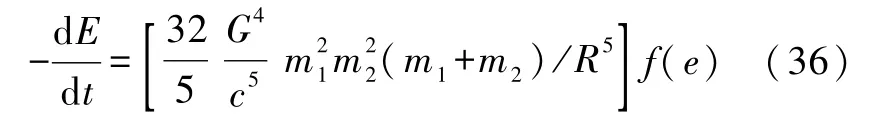
其中

式(36)中,e为偏心率,R为轨道半长轴的长度.对于一般双星有-dE/dt≈1.0×1029~1.0×1031erg/s,射到地球的能流为1.0×10-13~1.0×10-10erg/(cm2·s).
5 脉冲双星的引力辐射
1978年前后,泰勒 (J.H.Taylor)和休 斯(R.A.Hulse)通过对脉冲双星PSR1913+16(其中至少有一颗星是中子星)的长期观测,发现这对双星的公转周期每年减少约万分之一秒[9].他们研究认为,这是双星公转辐射引力波,造成公转能量损失导致的(图3).他们理论计算的结果与观测结果定量符合得很好.他们的工作被认为是发现引力波的第一个证据,虽然是间接证据.
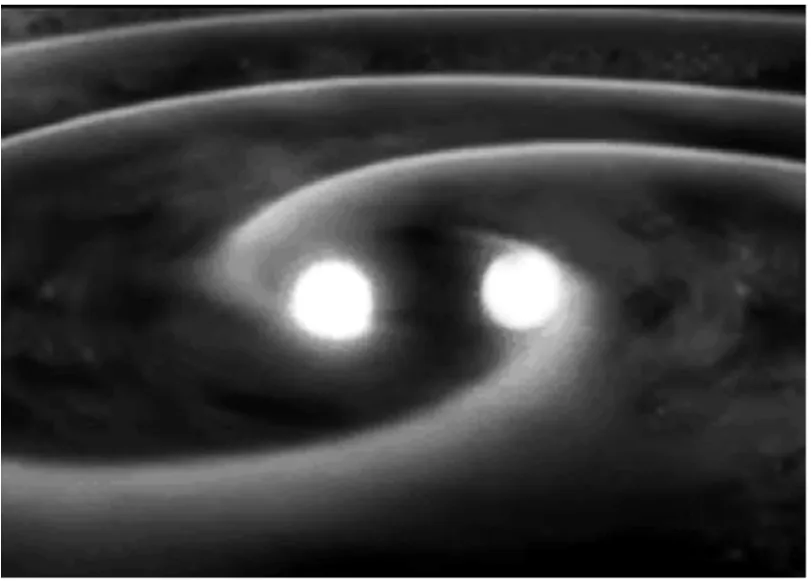
图3 脉冲双星辐射引力波
由于没有看到他们的具体计算过程,我们就用前面讲到的方法做了一下计算,可以得到与他们相近的结果[2,3,10-12].
设双星在 x-y平面内转动,取质心坐标系,m1、m2为两颗星的质量,d为两颗星的距离.从万有引力定律可以得到双星运动的轨道方程

式中a为椭圆轨道的半长轴,e为偏心率,ψ为公转角.
用式(23)可算出双星系统的非零四极矩
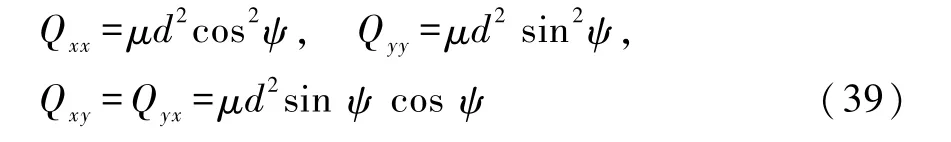
从开普勒第二定律(面积定律)可知,双星公转角速度为
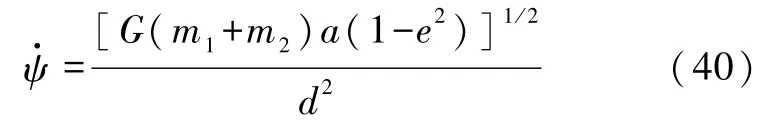
用式(27)可算出系统的放能率为
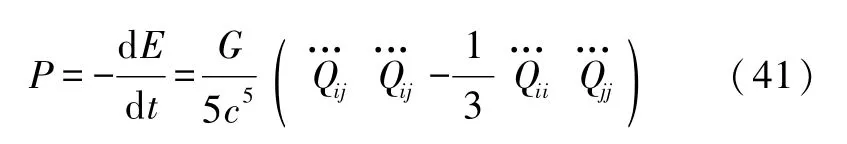
再用式(38)—式(40)算出质量四极矩的三阶导数,并把它们代入式(41),可算出双星在一个公转周期内的平均辐射功率为
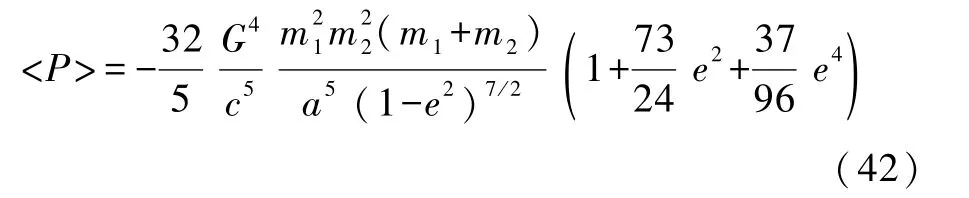
利用开普勒第三定律可算出公转周期变化率 T·b与辐射功率的关系
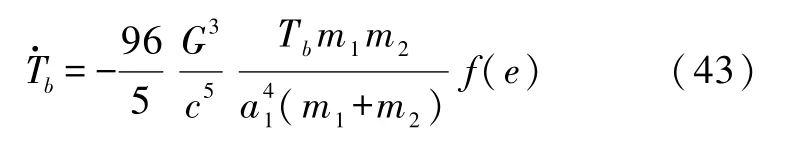
f(e)如式(37)所示.式中m1为主星质量,m2为伴星质量,a1由下式给出
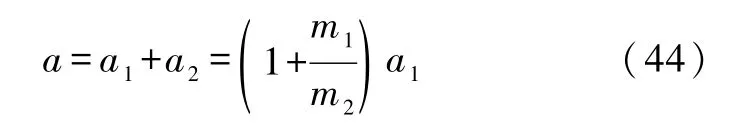
把泰勒等人公布的观测数据代入,可得引力辐射导致的周期减小的理论计算值为
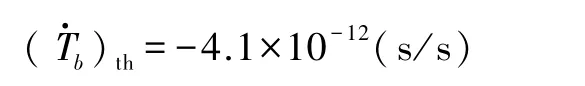
他们对周期减少的直接观测值为
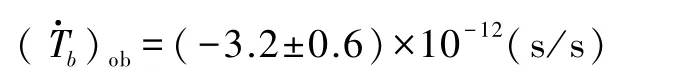
以上是我们1980年的计算结果,理论值与观测值的误差约28%[10,11].1981年,胡宁、章德海、丁浩刚用不同的方法在朗道表述和适当的坐标条件下,也算出了与观测基本一致的结果[12].1984年,郑玉昆用多种能量表述作了计算,也得到相似的结果[13].可见,上述计算的结果与“能量表述”无关.所以,虽然各种能量表述均有缺点,但用来计算引力辐射还都可以使用.
1989年,泰勒等人得到精确度更高的结果
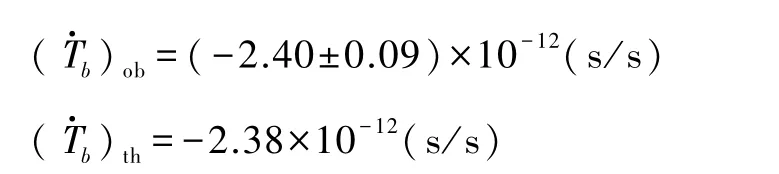
1993年,休斯和泰勒由于“对脉冲双星的研究开创了研究引力的新途径”,而获得了诺贝尔物理奖.为慎重起见,诺贝尔奖评委会未明确说明,真正的颁奖原因是“他们的观测证实了引力波的存在.”一般认为,休斯与泰勒对脉冲双星周期变化的研究结果,是引力波存在的一个可靠的间接证据.
6 引力波的探测
目前认为,宇宙中可能存在的引力波源,有以下几种情况[14].
1)两颗致密星相互靠近,直至碰撞、合并.
这两颗致密星,有可能是两颗中子星,也有可能是两个黑洞,或者一颗中子星与一个黑洞.它们围绕共同的质心旋转,不断辐射出引力波,而自身的引力势能不断减少,旋转周期不断减小.例如前面谈到的脉冲双星PSR1913+16就是这种情况.
随着公转周期的减小,相互旋转的两颗致密星会越来越靠近.研究表明,它们会接触、碰撞、合并,同时释放出大量引力波.例如这次探测到的GW150914事件,就很可能是两个黑洞合并而释放出的引力波造成的.研究表明,这次事件很可能是13.4亿年前,两个黑洞(质量分别为36M⊙和29M⊙)合并成为一个质量为62M⊙的黑洞造成的.在此过程中,有大约3M⊙的黑洞质量转化成了引力辐射能,形成强大的引力波信号.
2)非对称中子星
如前文所述,非对称(e≠0)的快速旋转的中子星,在诞生初期,会产生极强的引力辐射,辐射阻尼使中子星转速很快减慢,引力辐射随之逐渐减弱.
3)超新星爆发
研究表明,超新星的非球对称猛烈爆发,有可能产生很强的引力波.
4)原初引力波
在宇宙诞生的初期,由于初始的大爆炸,特别是随后的暴胀过程,会有原初引力波产生.这种原初引力波会与其他物质(宇宙微波背景辐射)产生相互作用,形成某些可观测的遗迹,保留到今天.
前面谈到的脉冲双星 PSR1913+16的周期变化,是人类第一次用间接的方法探测到引力波.那么有没有直接探测引力波的方法呢?这就需要提到以美国的LIGO为代表的地面引力波探测实验了[15].
实际上,早在上世纪60年代,美国物理学家韦伯,就试图利用引力波的偏振在大型金属圆柱体内造成的四极共振效应(力学效应),来探测引力波(图4).他在相距1000 km的两个地方设置了同样的装置.1969年他曾宣布收到频率为1660 Hz的来自银河系中心的引力波,但此后无法重复,最终结论被否认.今天看来,韦伯测到的信号肯定不是引力波[2,3,16].
LIGO也是利用引力波偏振造成的四极共振来探测引力波,不过它不是直接观测力学效应,而是观测精度更高的激光干涉效应.为此,美国在东南部的路易斯安那州的利文斯顿和西北部的华盛顿州的汉福德建造了两座激光干涉引力波观测台(图5),它们之间的直线距离大约有3 000 km.在LIGO的这两个观测台上各有一个L形真空管探测臂,两条臂长度各4 km(此外,在汉福德还有另外一台臂长2 km的激光干涉仪).每一座观测台实际上是一架迈克尔孙干涉仪,在两臂相交处有一个半透明半反射的镜片.在管的两端有反射镜,让激光束在镜面之间来回反射,以增加激光干涉的有效距离.因为存在光的来回反射,因此这一光学装置也可以看成由2个相互垂直的“FP(法布里-珀罗)干涉腔”组成.

图4 韦伯与他的引力波探测器

图5 位于美国东南部路易斯安那州和西北部华盛顿州的两座激光干涉引力波观测台
LIGO在相隔3000 km设两个观测台,是为了排除地球上的地震、雷击和火车行驶、飞机飞行等各种干扰因素,因为这些因素不可能在两地同时发生.而且,引力波的传播速度是有限的,可以通过两地的探测器探测到的引力波信号的时间差,来推断出引力波源的空间方位,并顺便验证一下引力波传播速度是光速的理论预期.
如果有引力波通过 LIGO,引力波的偏振效应(即图1与图2所示的“剪切效应”)造成时空畸变,会使相互垂直的探测臂一个伸长、一个缩短,不断交替(图6),这样就会引起光的干涉条纹的变化,从而被光电检测器探测到此变化的光学信号.通过这个变化的光学信号的理论分析,可以推论出到底是什么样的天体物理过程发射了该引力波.这一理论分析所依赖的模型是EOBNR模型[1].
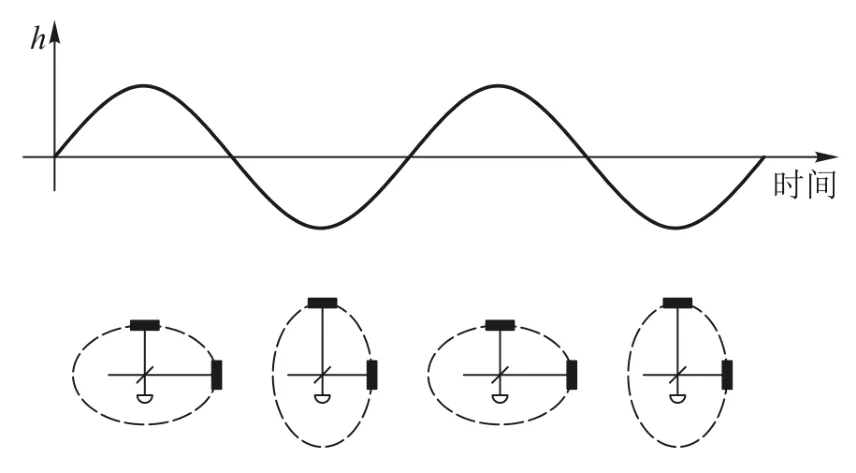
图6 LIGO的工作原理示意图
本次观测中,让激光在干涉仪中反射了400次,相当于把臂长(光路)加长到了1 600 km.这样,本次引力波引起的光路长度变化为质子半径(1.0×10-15m)的千分之一,即 1.0×10-18m.LIGO的灵敏度在2015年9月升级后达到1.0×10-23,恰好可以探测到这样的引力波信号.
LIGO设在利文斯顿的干涉仪首先收到信号,7 ms后汉福德的干涉仪也收到了这一信号.7 ms基本上是引力波以光速从利文斯顿到达汉福德所需的时间.这大大加强了本次观测的可信度[17].这次收到的信号,频率从刚开始的35 Hz上升到250 Hz,振幅很快达到最大值,然后频率基本保持不变,振幅逐渐减小,最后信号消失.信号持续时间约0.2 s(图7).
这非常像2个巨大的致密天体在相互围绕旋转中逐渐靠近、并合而发出的引力波(图8).在与事后用EOBNR理论模型计算,以及数值相对论模拟得到的大量各种参数的黑洞碰撞、并合的数据进行匹配对比后,LIGO团队认为,他们观测到的信号,可以用2个大质量黑洞(分别为36M⊙与29M⊙)并合为1个黑洞(62M⊙)时发射的引力波来解释.LIGO团队是在反复推敲他们的观测数据后,才正式发表观测结论的.所以,他们这次得到的引力波的报导是十分可信的.
LIGO激光干涉引力波探测器是目前地球上长度最长的地面引力波探测装置.除了LIGO,在欧洲还有Virgo,在日本还有KAGRA等规模小一些的地面引力波探测激光干涉仪,而且印度也将投资建设LIGO-India地面引力波探测激光干涉仪.
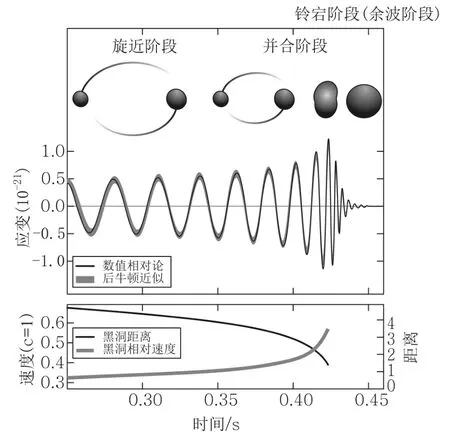
图7 LIGO收到的引力波信号

图8 产生引力波信号的黑洞并合模型
图9 空间引力波探测装置示意图
除了地面引力波探测装置,是不是还有卫星上的空间引力波探测装置呢?有,这就是原来的LISA计划(当时美国航天局还没有退出)和目前缩小了的eLISA计划.eLISA计划由欧洲空间局主导,其技术方案是将3对探测器送入太空,让它们组成等边三角形,相邻两对探测器之间的距离大约为5×106km,它们在地球后面以 20°的夹角一起绕太阳运行.3对探测器之间用激光精确测量距离.如果有引力波传来,它会挤压时空,使3对探测器之间的距离发生微小的变化.灵敏的激光干涉仪可测出一个原子直径大小的位移.由于它们所占的地域比地球上的探测器大得多,因而可能探测到波长更长、频率更低的引力波.
图10 利用脉冲星计时阵列探测引力波的示意图
除去用激光干涉仪探测之外,脉冲星计时阵列也可用来探测引力波(图10)[14,18].因为脉冲星具有稳定精确的脉冲周期,引力波的到来会改变脉冲星到地球的距离,从而使我们观测到脉冲星的脉冲周期发生变化.欧洲、北美、日本和澳大利亚都在做这方面的探测准备.

图11 西藏阿里天文台
中国目前有由中国科学院主导的“太极计划”和中山大学主导的“天琴计划”,其基本思想与eLISA类似,也是发射三颗卫星到天上去探测引力波.当然,“太极计划”还有一个备份方案,那就是中国直接参与eLISA计划,与欧洲合作来探测空间引力波.此外,还有中科院高能物理所主导的“阿里计划”.该计划准备进一步建设在西藏阿里地区的天文台,使之能够用来探测原初引力波(图11).此外,还有清华大学、北京师范大学、中国科技大学和中科院高能物理所等单位分别主导或参加的其他探测计划.目前“太极计划”、“天琴计划”和“阿里计划”等的最终实施细节还需要等待中国政府高层领导的决策.中国科学院已经先期支持了自己单位领衔的引力波探测计划,有的已经拨出专项研究经费.
[1] Abbott B P,et al.The LIGO Scientific Collaboration,Virgo Collaboration.Observation of gravitational waves from a binary black hole merger[J].Physical Review Letter,2016,116(6)016102. Doi:10.1103/Phys-RevLett.116.016102.
[2] 刘辽.广义相对论[M].2版.北京:高等教育出版社,2008.36-144
[3] 赵峥,刘文彪.广义相对论基础[M].北京:清华大学出版社,2010:16-71,102-121.
[4] 梁灿彬,周彬.微分几何入门与广义相对论[M].2版.北京:科学出版社,2006:188-245.
[5] 温伯格 S.引力论和宇宙论[M].邹振隆,张厉宁,等译.北京:科学出版社,1980.187-194,287-341.
[6] 朗道,栗弗席兹.场论[M].鲁欣,任朗,袁炳南,译.邹振隆,校.北京:高等教育出版社,2012:313-318,383-397.
[7] Misner C W,Thorne K S,Wheeler J A.Gravitation[M].SanFrancisco:FreemanWHCompany,1973:941-1044.
[8] 刘寄星.爱因斯坦和同行审稿制度的一次冲突[J].物理,2005,34:487.
[9] Huse R A,Taylor J H.Discovery of a pulsar in a binary system[J].Neutron stars,black holes,and binary X-ray sources,1975,48:433.
[10] 桂元星,赵峥,刘辽.PSR1913+16的重力辐射.北京师范大学学报(自然科学版)1980(3-4):67.
[11] 刘辽.刘辽文集[M].长沙:湖南科学技术出版社,2008:30-37.
[12] 胡宁,章德海,丁浩刚.双星放射引力辐射的阻尼力[J].物理学报,1981,30(8):1003.
[13] 郑玉昆.关于引力场的能量问题[J].物理学报,1981,30(1):46.
[14] 郭宗宽,蔡荣根,张元仲.引力波探测:引力波天文学的新时代[J].科技导报,2016,34(3):30.
[15] Abramovici A,Althouse W E,Drever R W P,et al.LIGO:Thelaserinterferometergravitationalwave observatory[J].Science,1992,256(5055):325-333.
[16] Weber J.Evidence for discovery of gravitational radiation[J].Phys Rev Lett,1969,22:1320-1324.
[17] 姬扬.引力波来了(编译自 Sung Chang,Physics Today,2016(4):14)[J].物理,2016,45(4):260.
[18] Sesana A,Vecchio A.Gravitational waves and pulsar timing:stochastic background,individual sources and parameterestimation [J].ClassicalandQuantum Gravity,2010,27(8):084016.
编者按:在大学物理教学中一般只讨论势能不随时间变化的功能原理,势能随时间变化的功能原理很少涉及,因此学生在遇到此情况时可能犯错误,甚至有些老师也不能免.朱如曾先生对此问题作了详尽说明,并给出实例,是一篇值得注意的文章.
Gravitational wave and general relativity
ZHAO Zheng1),LIU Wen-biao1),ZHANG Xuan-zhong2)
(1.Department of Physics,Beijing Normal University,Beijing 100875,China;2.Beijing Science and Technology Association,Beijing 100101,China)
The theory about gravitational wave is introduced based on the general relativity.We introduce how to detect indirectly gravitational radiation by means of the time rate variation of the period of binary star and how to directly detect gravitational waves by means of the polarization of the wave.
gravitational wave;general relativity;binary star;polarization;LIGO
O 412.1
A
1000-0712(2016)10-0001-10
2016-05-10
国家自然科学基金项目(11235003)资助
赵峥(1943—),男,江西萍乡人,北京师范大学物理学系教授、博士生导师,主要从事理论物理的教学和研究工作.
