基于RD谱轮廓线的高频地波雷达二阶谱提取*

楚晓亮, 张 杰, 纪永刚, 王祎鸣,于长军

(1.国家海洋局 第一海洋研究所，山东 青岛 266061； 2.中国海洋大学，山东 青岛 266100；3.哈尔滨工业大学(威海)，山东 威海 264209)



基于RD谱轮廓线的高频地波雷达二阶谱提取*

楚晓亮1,2, 张 杰1, 纪永刚1, 王祎鸣1,于长军3

(1.国家海洋局 第一海洋研究所，山东 青岛 266061； 2.中国海洋大学，山东 青岛 266100；3.哈尔滨工业大学(威海)，山东 威海 264209)

雷达回波谱中的噪声和目标回波会对二阶谱的提取造成困难。基于地波雷达海面回波谱特性，提出了一种采用距离-多普勒谱(RD谱)轮廓线结合一阶和二阶谱特点的二阶谱提取方法。此方法可以通过计算机自动实现对二阶谱的提取，有利于大批数据的分析和工程化系统的实时处理。利用该方法对典型实测雷达回波数据进行了处理和分析。结果表明，RD谱轮廓线能够反映一阶谱和二阶谱的特征，并且不易受噪声和目标的影响；从RD谱轮廓线获得的二阶谱分界点，可以为一维多普勒回波谱中的二阶谱提取提供参考，能够较好地避免由于目标和噪声的影响而导致的二阶谱边界误判问题，准确地分离二阶谱。

高频地波雷达(HFSWR)；RD谱； 海态；二阶谱

高频超视距雷达可实现海上船只和低空飞机等目标的超视距探测及海洋动力过程的连续观测，具有观测距离远、覆盖面积大、工作全天候等优点。高频地波雷达的回波谱中含有丰富的海洋动力环境参数信息，因此可以从回波谱中提取海面流场、风场和海浪谱等信息，这为海洋动力学环境探测提供了新的手段。20世纪70年代Barrick等[1-3]提出了高频地波雷达一阶和二阶散射截面方程，为高频地波雷达海态反演提供了理论基础，由此人们开展了大量的海态信息提取工作[4-11]。由于海态信息主要包含在高频地波雷达多普勒回波谱中的一阶谱和二阶谱中，故利用回波谱反演海态信息时，需先从回波谱中分离出一阶谱和二阶谱。目前，从雷达回波多普勒连续谱中提取一阶谱用于流场的反演，已有相关的研究[12-13]。而风浪等海态信息主要包含在高频地波雷达回波谱的二阶谱中，人们通常对二阶谱进行提取并分析处理来获得风速、有效波高和海浪谱[4-11]。相对于一阶谱，二阶谱的信噪比较低，并且展宽明显，易受目标信号的影响。尤其是实测雷达回波数据中的噪声和目标信号会影响二阶谱范围的确定，从而影响风速、有效波高等海态信息的反演结果。因而，如何有效地从回波谱中分离出二阶谱显得尤为重要。通常情况下，通过目视解译结合经验等人工方法可以从回波谱中分离出二阶谱，但这种方法不利于大批数据的分析和工程化系统的实时处理，因此需要建立从回波谱中提取二阶谱的程序化方法。本文基于地波雷达的海洋回波谱特性，提出了采用距离-多普勒谱(Range Doppler Spectrum， RD谱)轮廓线结合一阶和二阶谱特点提取二阶谱的方法，利用此方法针对典型的实测数据进行了二阶谱的提取,以期避免目标回波对二阶谱提取的影响，从而通过计算机自动地实现二阶谱的准确提取。

1 高频地波雷达回波谱分析

高频地波雷达回波谱中的一阶谱是由海浪与雷达电磁波发生布拉格散射后回波信号相互累加而产生的，在回波谱中占主导地位。在无海流的情况下，一阶谱表现为频率上的冲激函数，但在实际中由于雷达散射区域内变化的海流导致一阶谱展宽。

Barrick模型用2个冲击函数表示返回的一阶谱[1]，其散射截面方程可表示为

(1)

根据电磁波海面的作用理论，在无海流的情况下，一阶谱的谱峰位于±ωB处，而ωB与k0之间满足深水色散关系：

(2)

式中，g为重力加速度。若存在海流时，可根据一阶峰偏移±ωB的大小来求出海流的流速。

高频无线电波与海浪还存在高阶作用，Barrick[2]将无海流情况下的二阶散射截面用一个方程表示为

(3)

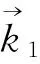
图1 频率为13.02 MHz的地波雷达的一维多普勒谱

不同距离单元处的一维多普勒谱构成了二维RD谱，图2给出了频率为13.02 MHz的地波雷达的实测RD谱图。从图中看出，RD谱图中出现明显的一阶谱和二阶谱特征，并且一阶和二阶谱随距离分布趋势与回波功率分布趋势相似。因此，如对RD谱进行边缘检测，勾勒出RD谱中的一阶、二阶多普勒的轮廓，就能确定二阶谱大概位置。基于这一思路，可先提取RD谱中的一阶谱和二阶谱的轮廓线，确定一阶谱和二阶谱大致的范围，然后再精确确定二阶谱边界。

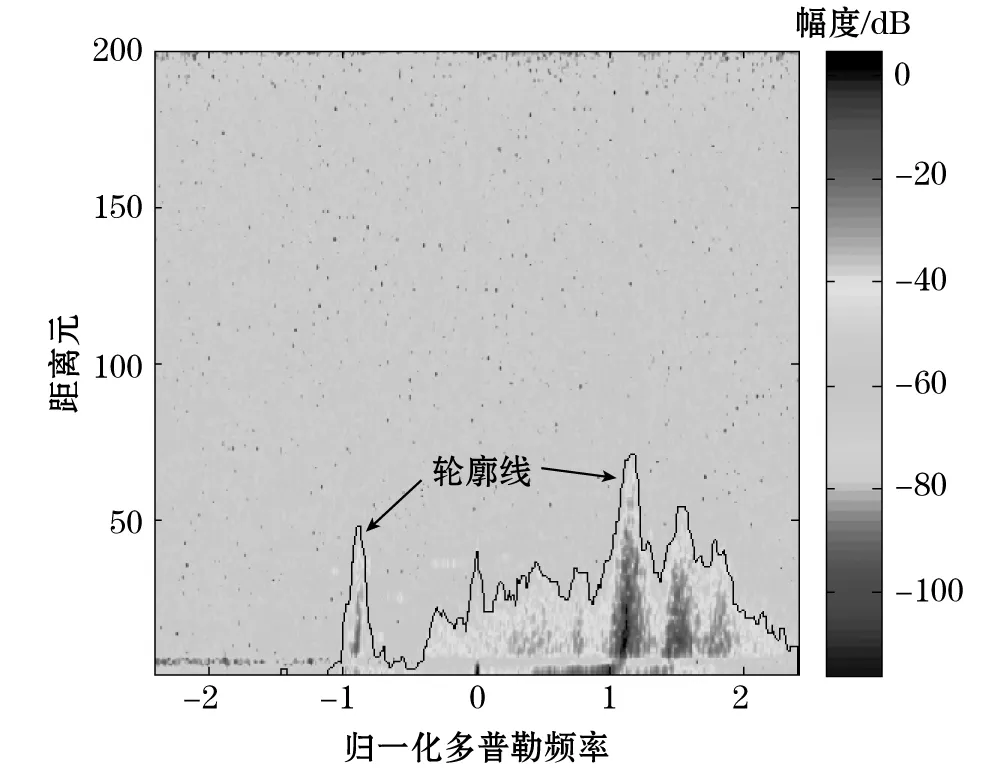
图2 频率为13.02 MHz的雷达RD谱及其轮廓线

2 二阶谱提取的方法

二阶谱的提取流程如图3所示。首先选取RD谱，利用参考单元的噪声估计值作为门限，可以得到RD谱的二值化图像。在只含有“0”和“1”的二值图像中，值全为“1”的像素点将相互连接在一起成为一个连通域，提取这个连通区域的轮廓，就可以得到图像的轮廓曲线，如图2所示。从图2中可以看出，轮廓线的趋势、峰值基本能够反映出RD谱一阶谱和二阶谱的特征，即轮廓线起伏趋势实际上也具备了多普勒回波谱的特征。接着对轮廓线进行匀滑，以防止由噪声等造成的抖动而加大寻找边界难度。再结合二阶谱的特征，通过搜索判断获得轮廓线中二阶谱的分界点。

图3 二阶谱提取流程

搜索轮廓线中的二阶谱分界点是相对比较关键的操作，因为由此可确定二阶谱的大致范围，为后续的一维多普勒谱中的二阶谱分界点搜索提供依据。具体操作步骤：1)确定左右一阶谱峰的大致位置。2)选择二阶谱的大致范围。考虑到能够满足反演海浪谱需要的二阶谱区域通常为0.6ωB<|ω|<0.9ωB和1.1ωB<|ω|<1.4ωB[9]，在实际中选择二阶谱范围的时候可以在此基础上稍微扩大一些，同时也要考虑到海流引起的多普勒谱的频移。3)在选择的二阶谱范围内搜索极值点，即搜索此范围内的所有极大值与极小值点，如果存在则进行下一步，如果不存在则说明无二阶谱的存在。4)结合二阶谱的特点，分别搜索左右一阶峰两侧极值点的匹配点。5)在匹配的极值点中获得一阶峰两侧极小值匹配点。6)计算同侧极小值包含区域的信噪比。7)判断信噪比是否大于阈值，如果“是”则此极小值即为二阶谱分界点，如果“否”则认为多普勒谱中没有可用于反演的二阶谱。为了获得较高的海浪谱反演精度，信噪比阈值可以选择为15 dB[16]，通常情况下信噪比阈值可选为5 dB[17]。通过以上操作就可以获得轮廓线的二阶谱分界点。

将得到的轮廓线的二阶谱分界点作为参考值，搜索某一距离元处的一维多普勒谱的二阶谱分界点，其步骤与上述过程类似。搜索过程中若有噪声或目标回波的干扰，轮廓线的二阶谱分界点就成为重要的判断标准，确保准确地确定一维多普勒谱中的二阶谱范围。

3 数据处理及结果分析

利用二阶谱提取方法对图2的数据进行了处理，在获得谱轮廓线后，对其进行匀滑峰并确定峰值点和边界点。正一阶峰两侧的二阶谱的边界点和峰值点用星号表示，结果如图4所示。其中，4个边界点的坐标分别是0.646 2，0.861 6，1.358 6和1.706 5。结合图2可以看出，获得的二阶谱轮廓线的分界点能够反映二阶谱在RD谱上存在的大致范围。对于某一距离上的多普勒谱，可按照上述步骤搜索二阶谱的分界点，搜索过程中受噪声等因素的影响会比较大，但以轮廓线的分界点为参考，可以大大降低这种影响，并可准确地获得二阶谱的分界点，从而提取出二阶谱。图5给出的是图2中第15个距离单元处的一维多普勒谱，以图4中获得的二阶谱轮廓线的边界点为参考，对一维多普勒谱进行搜索就可以比较容易地确定二阶谱范围，如图5中灰色区域，其二阶谱4个边界点的归一化多谱勒频率分别为0.646 2，0.886 4，1.358 6和1.690 0，这与轮廓线的二阶谱分界点归一化多普勒频率略有差异。

图4 轮廓线二阶谱特征点的提取

图5 一维多普勒谱中二阶谱的提取

在实际探测中，船只等目标会在雷达多普勒回波谱中产生较强的回波，这会对二阶谱的提取造成干扰，计算机在自动提取二阶谱边界时容易产生误判，利用本文的方法能够最大限度地排除这种干扰，准确地提取二阶谱。为了说明本文方法的有效性，我们给出了工作频率为11.07 MHz的地波雷达实测RD谱作为个例，如图6a所示，图中的二阶谱较图2来说相对较弱，而RD谱中的目标较为明显。利用本文方法对含有目标的多普勒谱进行二阶谱分离，首先对RD谱进行谱包络线的提取，提取结果如图6b所示，可以看出目标对轮廓线基本上没有影响。进而可以获得二阶谱轮廓线的边界坐标。选取RD谱上第16距离单元格和12距离单元格的一维多普勒谱，分别含有目标1和目标2的信号，如图7和图8所示。图7中，目标1靠近右侧一阶峰，并且幅度较大，这通过曲线平滑是消除不掉的。另外，目标1和其他目标相对于右侧一阶峰近似对称，若直接对一维多普勒谱来提取二阶谱，会因受目标回波的影响，易将目标误当成二阶谱，使二阶谱的边界点出现误判，从而不能正确地提取二阶谱。而轮廓线则不受目标的影响，所以借助于谱轮廓线中的二阶谱边界点，可以正确分离一维多普勒谱中二阶谱的区域，如图7中的灰色区域。由图8可知，右侧一阶峰旁的二阶峰出现明显分裂。结合图6的RD谱及上述分析，出现谱峰分裂是由于目标2的信号叠加到了二阶谱上，从而对二阶谱的提取造成影响，即在提取过程中有可能把2个峰值间的波谷误认为是二阶谱的分界点，或把左侧稍高的峰当作二阶谱的峰值。采用本文方法，轮廓线得到的二阶谱峰值归一化频率为1.475，而图8中二阶谱中左侧峰值(目标2峰值)归一化频率为1.34，二者相差较大，很容易将此峰值排除，从而获得二阶谱范围，如图中灰色区域。若要对二阶谱中的目标进行消除，可以考虑利用CFAR检测方法检测出目标后[18]，将目标所占的单元格用周边无目标的单元格的均值代替，消除目标对海杂波的影响。也可以借鉴海杂波循环对消方法[19]，将目标消除，这样就可以将二阶谱提取出来，如图9所示。为了进一步通过实测数据验证本文方法，我们给出了工作频率为13.02 MHz的雷达回波谱的二阶谱提取结果(图10)，所采用的数据与图2相比，除雷达频率相同外，实际海况条件和时间都不相同。结果显示，本文方法依然可以对二阶谱进行正确的提取。

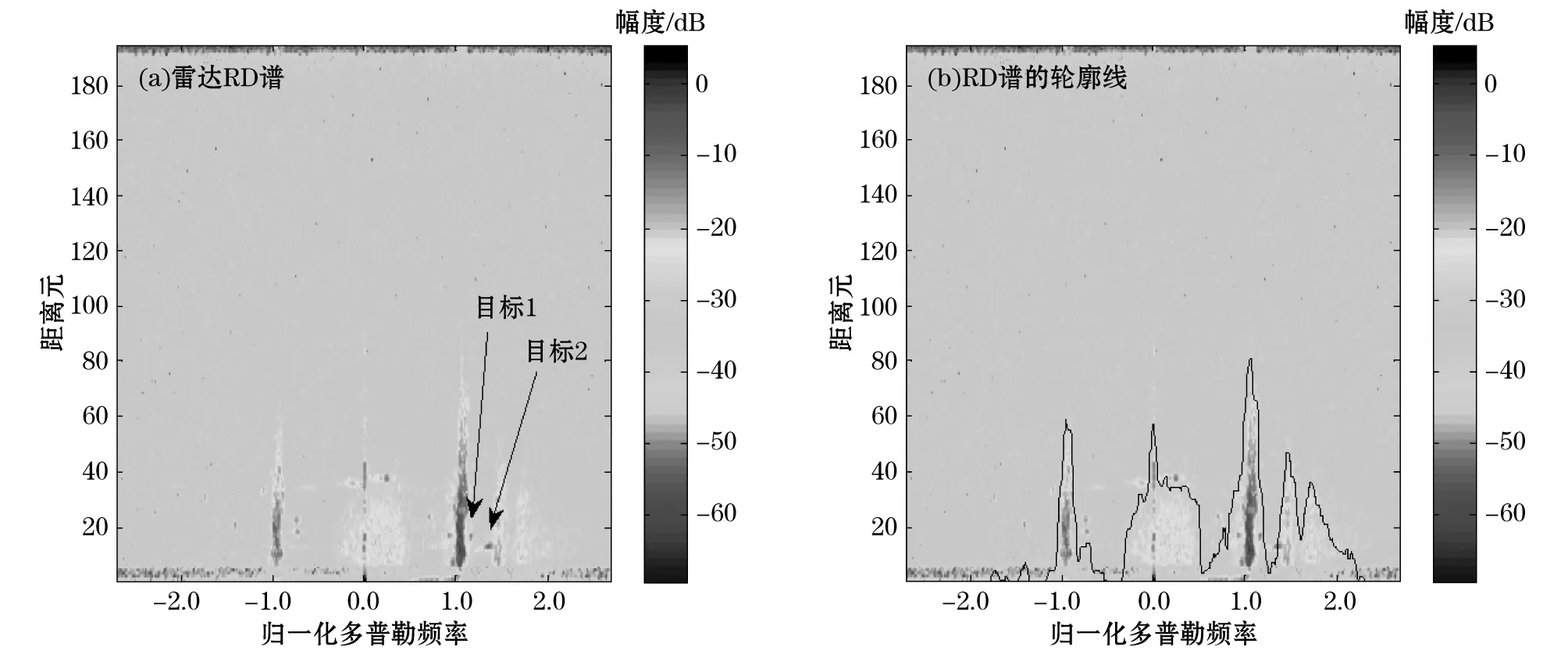
图6 频率为11.07 MHz的雷达RD谱

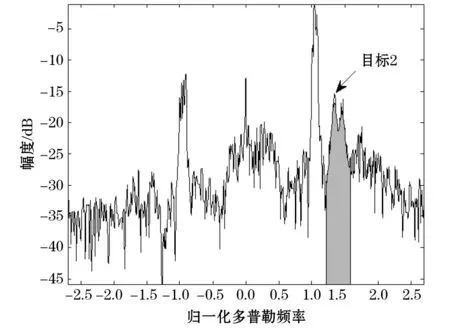
图8 第12距离单元的多普勒谱图

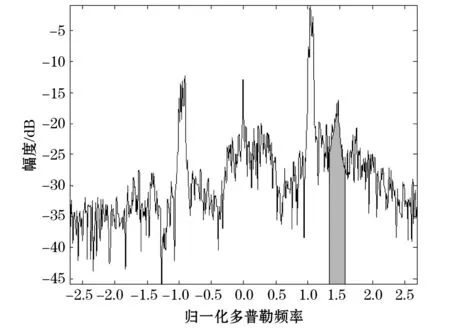
图9 第12距离单元的二阶谱提取

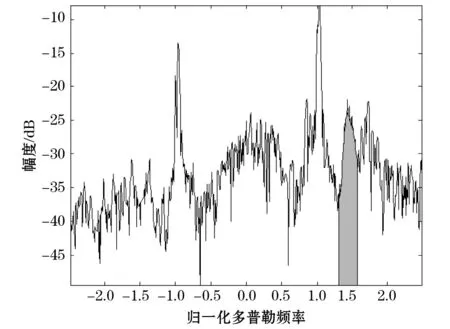
图10 频率为13.02 MHz的雷达回波谱的二阶谱提取

4 结 语

利用高频雷达数据反演风速、有效波高等海态信息时，需要从雷达回波谱中提取二阶回波谱。本文基于地波雷达的海洋回波谱特性，提出了采用RD谱轮廓线结合一阶和二阶谱特点的二阶谱提取方法，此方法可以通过计算机自动实现对二阶谱的提取，有利于大批数据的分析和工程化的系统实时处理。为了验证该方法的性能，本文选取了典型实测雷达回波数据进行处理和分析，从实测数据处理结果来看，本文所提出的方法可避免噪声和目标对二阶谱提取的影响，能够准确地分离二阶谱，具有一定的实用性。由于本文所采用验证的实测数据比较有限，对本文的方法还需要选取不同实验地点、不同海况条件的大量实验数据来进行验证和完善，以进一步提高其可靠性。

[1] BARRICK D. First-order theory and analysis of MF/HF/VHF scatter from the sea[J].IEEE Transactions on Antennas and Propagation, AP-20(1), 1972:2-10.

[2] BARRICK D. Remote Sensing of sea state by radar[C]∥IEEE International Conference on Engineering in the Ocean Enviroment,Newport:IEEE 1972:186-192.

[3] WEBER B L, BARRICK D E. On the nonlinear theory for gravity waves on the ocean's surface. Part I: derivations[J]. Journal of Physical Oceanography, 1977,7(1):3-10.

[4] BARRICK D E, WEBER B L. On the nonlinear theory for gravity waves on the ocean's surface. Part II: interpretation and applications[J]. Journal of Physical Oceanography, 1977,7(1):11-21.

[5] LIPA B. Inversion of second-order radar echoes from the sea[J].Journal of Geophysical Research: Atmospheres, 1978, 83(c2): 959-962.

[6] LIPA B, BARRICK D. Extraction of sea state from HF radar sea echo: Mathematical theory and modeling[J]. Radio Science, 1986, 21:81-100.

[7] WYATT L R. High-frequency radar measurements of the ocean wave directional spectrum[J]. IEEE Journal of Oceanic Engineering, 1991, 16(1):163-169.

[8] HOWELL R, WALSH J. Measurement of ocean wave spectra using narrow-beam HE radar[J]. IEEE Journal of Oceanic Engineering, 1993,18(3):296-305.

[9] HISAKI Y. Nonlinear inversion of the integral equation to estimate ocean wave spectra from HF radar[J]. Radio Science, 1996,31(1): 25-29.

[10] GREEN J J, WYATT L R. Row-action inversion of the Barrick-Weber Equations[J].Journal of Atmospheric and Oceanic Technology, 2006,23(3): 501-510.

[11] ESSENH H H. GURGEL K W, SCHLICK T. Measurement of ocean wave height and direction by means of HF radar: An empirical approach[J]. Deutsche Hydrografische Zeitschrift, 1999, 51(4):369-383.

[12] YANG S L, KE H Y, HOU J C, et al. Super-resolution ocean surface current algorithm based on MUSIC for OSMAR 2000[J].Journal of Wuhan University(Natural Science Edition),2001,47(5)：601-608.杨绍麟,柯亨玉,侯杰昌,等.OSMAR2000基于MUSIC的超分辨率海洋表面流算法[J].武汉大学学报(理学版),2001,47(5)：601-608.

[13] MIDDLEDITCH A ,WYATT L R.An instantaneous-frequency filtering technique for High-Frequency radar oceanography[J]. IEEE Journal of Oceanic Engineering, 2006,31(4): 797-803.

[14] JI Z Y, MENG X D,YUAN Y S. Analysis and emulation for second order sea clutter in research of sea clutter in HF ground wave over-the-horizon radar[J].Modern Radar,2003，25(4): 4-6.冀振元,孟宪德,袁业术. 高频地波OTH雷达二阶海杂波分析及模拟[J].现代雷达,2003,25(4): 4-6.

[15] SHEARMAN E D R. Radio science and oceanography[J]. Radio Science, 1983, 18(3): 299-320.

[16] WYATT L R. Limits to the inversion of HF radar backscatter for ocean wave measurement[J]. Journal of Atmospheric and Oceanic Technology,2000, 17(17): 1651-1666.

[17] WU X B, LI L, LI Y, et al. Experimental research on significant wave height detecting with HFSWR OSMAR071[J]. Oceanologia Et Limnologia Sinca, 2012,43(2):210-216.吴雄斌,李伦,李炎,等.高频地波雷达海面有效波高探测实验研究[J].海洋与湖沼， 2012，43(2): 210-216.

[18] PONSFORD A M, WANG J. A review of high frequency surface wave radar for detection and tracking of ships[J]. Turkish Journal of Electrical Engineering Computer Sciences,2010,18(3):409-428.

[19] GUO X, NI J L, LIU G S. The ship detection of sky wave over the horizon radar with short coherent integrationtime[J].Journal of Electronic and Information Technology,2004，26(4):613-618.郭欣，倪晋麟，刘国岁.短相干积累条件下天波超视距雷达的舰船检测[J].电子与信息学报，2004，26(4):613-618.

Received: August 14, 2014

The Second Order Spectrum Extraction From High Frequency Ground Radar Sea Echoes Based on the Outline of the RD Spectrum

CHU Xiao-liang1,2, ZHANG Jie1, JI Yong-gang1, WANG Yi-ming1, YU Chang-jun3

(1.TheFirstInstituteofOceanography,SOA, Qingdao 266061，China;2.OceanUniversityofChina, Qingdao 266100, China; 3.HarbinInstituteofTechnology，Weihai， Weihai 264209,China)

The noise and the target echo signal existing in the Hgh Frequency Surface Wave Radar (HFSWR) echoes can cause trouble for extraction of second order spectrum. According to the characters of the HFSWR echoes, a method exploring the outline information of the Range Doppler (RD) spectrum in combination with the features of the first and second spectrum is presented in this paper. The method can be implemented to extract the second order spectrum by computer, which is conducive to amounts of data analysis and the real time processing data by engineering system. This method is applied to the typical radar data processing and analysis, and the results show that the features of the first and second spectrum can be reflected by the outline of RD spectrum which is not influenced by noise and target echo. Based on the second spectrum boundary points obtained from the outline, the issue of boundary error judgment due to the influence of the noise and the target echo can be avoided, when the second spectrum is extracted from the one dimensional Doppler spectrum echo.

High-Frequency Surface Wave Radar(HFSWR); Range Doppler Spectrum; sea state; second order spectrum

2014-08-14

国家自然科学基金重点项目——高频天波/地波集成技术非协作目标信息获取与处理(61032011)；中国博士后科学基金项目——天地波集成体制超视距雷达海浪反演研究(2013M531559)

楚晓亮(1977-)，男，山东平度人，讲师，博士，主要从事高频地波雷达及X波段导航雷达海态反演方面研究.E-mail：xlchu@ouc.edu.cn

(王 燕 编辑)

TN958

A

1671-6647(2016)01-0114-07

10.3969/j.issn.1671-6647.2016.01.011