基于观测资料的海浪与混合层深度相关性分析*

石永芳，尹训强,2，杨永增,2*

(1.国家海洋局 第一海洋研究所，山东 青岛 266061；2.海洋环境科学与数值模拟国家海洋局重点实验室，山东 青岛 266061)



基于观测资料的海浪与混合层深度相关性分析*

石永芳1，尹训强1,2，杨永增1,2*

(1.国家海洋局 第一海洋研究所，山东 青岛 266061；2.海洋环境科学与数值模拟国家海洋局重点实验室，山东 青岛 266061)

从观测数据角度出发，考察海浪与上层海洋混合层深度的变化关系。采用卫星高度计和三套温度观测数据，利用改进的混合层深度提取方法，获得海洋混合层深度。简要分析了多年月平均的有效波高和混合层深度的空间分布特征及时间变化规律，并进一步分析了它们的相关性。二者直接相关性分析的结果表明，在南北半球的中纬度地区二者的相关系数较大，而赤道地区较小。滤除年周期的气候态月平均场后，计算的距平相关系数在赤道区域较小；但在太平洋东部、南部和南印度洋存在一个大值区。此外，进一步研究了有效波高和混合层深度年际距平的相关系数，其空间分布特征与二者的距平相关系数的分布特征类似。为探究混合层深度的影响因素，同时也分析了风场与混合层深度的相关系数。综合上述结果，海浪和上层海洋的混合层深度之间存在着一定的相关性，海浪过程是风输入能量向次表层海洋传播的一个重要途径。

有效波高；混合层深度；相关性分析

海洋系统是一个有机的整体，各种海洋现象及物理过程相互影响相互联系。海洋上混合层是大气与海洋之间动量、热量和质量交换的中介，海浪又是存在于海气界面上的一种重要运动形态，其对海洋上混合层的动力及热力过程有重要影响。Wang和Huang[1-2]估算了风应力输入给海洋Ekman层的能量约2.4 TW，然而风输入给海浪的能量达到60 TW。Teng等[3]基于MASNUM全球海浪模式，数值估计了2005年风输入给海浪的能量约为57 TW，而深水区域的波浪破碎损耗的能量约为33 TW。这些输入给海浪的能量及损耗必然对上层海洋产生影响。波浪是风对海洋作用的最直接体现，决定着海表的动量、热量、湿度和质量交换(Makin和Kudryavtesev)[4]。波浪破碎、波生湍流、波动输运通量剩余量都是影响上混合层的重要物理过程。孙群[5]利用WAM模式研究了波浪破碎对混合层的影响。结果表明，当考虑波浪破碎对混合层的影响时，混合层深度加深了约50 cm，并且在混合层加深过程中，混合层达到某一深度所需时间明显提前。Yuan等[6]基于高确定性闭合假定和关于湍流动能耗散率的观测事实，通过海浪生湍流平衡解给出了该混合系数的机制解析，揭示了波生湍流混合的事实。Yang等[7]通过在特征尺度上雷诺平均的方法给出了波浪输运通量剩余量的参数化方案。基于以上理论的数值实验结果显示：考虑波浪作用的耦合模式，在整体上大幅度改善了海洋上混合层的模拟结果(Qiao等[8];Wang等[9])。由此，从理论分析和数值模拟的角度验证了波浪对上混合层的重要性。

前人的工作[10-12]主要采用理论分析和数值模拟的研究方法，基于观测资料探讨海浪与混合层深度(Mixing Layer Depth，MLD)之间的相关性分析目前还未见报道。本文从观测数据的分析角度出发，利用卫星高度计数据，获得世界大洋有效波高(Significant Wave Height，SWH)的分布。基于Argo温度剖面数据、 GTSPP数据和SubTS温度数据，分别计算了全球范围的混合层深度，定性分析了混合层深度与海浪有效波高的空间分布特征和时间变化规律。在此基础上，对有效波高与混合层深度两者的相关关系进行了统计分析。本研究旨在利用观测数据探讨海浪和上混合层的联系，为分析探讨上层海洋与大气各物理过程的相互作用奠定基础。

1 数据与方法

1.1 数据介绍

Topex/Poseidon和JASON-1卫星高度计是近年来海洋领域科学研究的一个重要数据来源(http://www.aviso.altimetry.fr/en/data/data-access/ftp.html) ，它们都是精确的循环轨道，轨道倾角为66°，所以只能在66°N-66°S的区域内运行，不能覆盖到极地地区；它们对地采样模式相同，为每秒测量1个点，星下点的地面分辨单元距离为6 km，循环周期约为10 d。数据有覆盖面积大、观测精度高、准同步的特点。

Argo是由高技术组成的、全新的、自动沉浮的浮标阵系统的简称(ftp:∥www.usgodae.org/pub/outgoing/argo/)。这种新型的、沉浮式浮标，可以获得海水内部不同层次的海流、温度、盐度等资料，为人类研究深层海洋提供了大量、密集和准实时、准同步的温盐资料。浮标数量虽然逐年不断增加，但直到2005年之后数据才可以覆盖中高纬区域，而在50°N以北、50°S以南及近海区域数据量仍然较少，这就为在全球范围内对混合层要素的研究增加了难度。

GTSPP数据(全称为Global Temperature-Salinity Profile Program)是由美国国家海洋数据中心提供的温盐数据集(http://www.nodc.noaa.gov/GTSPP/document/datafmt/ncfmt.html)。它与Argo数据类似，同样是温盐剖面数据，但时间序列是从1990年至今共20余a，比Argo数据长很多，而且GTSPP数据的密度更大，覆盖范围上两套数据相差不大，GTSPP数据在高于50°N/S区域的数据量仍然较少。

SubTS数据(全称为Sub-surface Temperature and Salinity)，是由Argo浮标数据、最新的GTSPP数据等多个数据集经客观分析得到的月平均温盐格点再分析数据( http://rda.ucar.edu/datasets/ds285.3/)。该数据的垂向分为17层，最大水深700 m，水平方向是1°×1°的规则网格。数据为1945-2006年，时间序列比较长、覆盖范围也较广。

本文使用了1993-2009共17 a的有效波高和风场数据(Topex/Poseidon(1993-2001)，JASON-1(2002-2009))[13]，2003-2009的Argo温度和盐度数据、1993-2006的GTSPP温度和盐度数据及1993-2009的SubTS温度和盐度数据开展计算分析。

1.2 混合层信息提取方法

在海洋上层，由于外界作用形成一层温度与密度较均匀的水层即上混合层，在混合层底部，存在温度随深度增大而快速下降的水层，即温跃层。本文近似地将混合层深度与温跃层上界深度等价来提取混合层深度。首先采用垂直梯度法即在浅海(水深≤200 m)采用0.2 ℃/m，开阔海区(水深>200 m)采用0.05 ℃/m的最低判定标准[13]。因为Argo和GTSPP数据在近岸数据量较少，在做数据处理时剔除了小于200 m的区域，选择0.05 ℃/m的最低判定标准。但是在提取混合层深度时发现单一的判定标准在高纬地区并不合适，这是因为，在中高纬区域，虽然剖面梯度较小，但实际也存在混合层，如果只单纯地选取0.05 ℃/m作为判定标准，在高纬地区则不能准确地判定混合层。这样不同区域的温度剖面应该根据剖面的自身特性选择不同的判定标准。为此，我们改进了垂直梯度法，取每个剖面垂直梯度最大值的某个百分比作为这个剖面混合层深度的临界值并且利用三次样条插值方法将数据插值到10 m层上。通过大量温度剖面的实验证明，选取最大梯度的70%较为合适。以4个不同纬度的温度剖面为例(图1)可以看出，最大梯度百分比的判定方法可以更准确地确定混合层深度，克服了垂直梯度法中单一判定标准遇到的问题。

图1 不同断面的温度分布及其相应的混合层(黑线)深度

1.3 散点数据插值及相关性分析方法

Topex/Poseidon、JASON-1的高度计数据和Argo、GTSPP获取的混合层深度数据都是不规则的散点数据，不适合进行相关性分析。为了得到规则网格化的数据，本文采用客观分析中较为经典的形式，即Cressman[15]提出的Cressman线性插值，将有效波高和混合层深度的散点数据插值到1°×1°的规则网格上。

通过计算相关系数描述海浪与混合层深度的相关性，相关系数越大，相关程度也越大；反之亦然[16]。由于有效波高平方与海浪能量的变化具有较为一致的变化特征，本文采用有效波高的平方，而非有效波高。

2 有效波高和混合层深度的时空分布特征

2.1 有效波高的空间分布

图2是1993—2009年月平均有效波高的空间分布，4个季节的典型月份(1，4，7和10月)显示出了全球有效波高明显的季节变化特征。结果表明：1月，等波高线分布表现为显著的北强南弱的马鞍形分布特征，北半球最大有效波高为6 m，出现在北大西洋，此时南半球有效波高随南纬增大而增大，最大值出现在45°S～50°S，约为4.5 m；7月，等波高线分布则表现为显著的南强北弱的分布特征，北半球的大西洋和太平洋有效波高普遍较小，在2.0～2.5 m，阿拉伯海区域存在波高极值区域，为3.5 m，7月南半球的有效波高则普遍较大，中高纬度区域均大于3 m，最大值出现在印度洋南部，为6 m；4月和10月的最大波高都出现在南半球，这一格局主要是由于南北半球海陆分布的差异而造成的，南半球稳定的西风带区域，风区较长。低纬度区域的有效波高常年保持较小值。

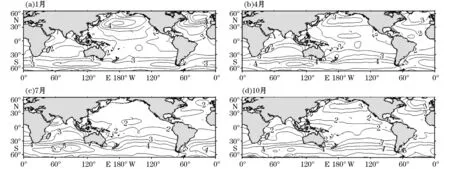
图2 月平均有效波高(m)空间分布图

2.2 混合层深度的空间分布

利用Argo(2003—2009年)、GTSPP(1993—2009年)和SubTS(1993—2006年)三套不同的温度剖面资料，提取对应的混合层深度，对处理到空间网格内的数据进行多年月平均，下面选取4，7，10和1月来分析混合层深度的空间分布特点。这与海洋中典型代表月份的选取有所不同，这样选取是为了同海浪分析相对应。

图3是Argo、GTSPP和SubTS三套数据多年月平均混合层深度的空间分布，3套数据的混合层深度的总体空间分布特征相似；由于Argo和GTSPP温度数据是不规则、不均匀的散点数据，在2005年之前2套数据并不能覆盖全球，特别是在高纬和近海区域数据量较少。因此，数据网格化插值在这些区域会造成相对大的误差。

混合层深度有显著的季节变化特征。冬季，太阳辐射最弱，是全年温度最低的季节，海面不断冷却，对流混合增强，加上风和浪的搅拌混合作用增强了上层海水的混合，混合层较深。夏季，太阳辐射最强，使海洋表层水温普遍升高，成为全年水温最高的季节，因表层增温快，深层增温慢，加上夏季对流、涡动混合弱，上层海水混合不强，混合层较浅。1月混合层深度大值区主要分布在北太平洋和北大西洋，而南半球中高纬度的混合层深度普遍较小。混合层深度在7月的空间特征与1月相反，主要呈现出南深北浅态势，大值区包含了南半球的大部分和北半球赤道附近区域，北半球中高纬度的混合层深度普遍较小。春、秋季节是混合加强和减弱的过渡期。春季，海面温度不断升高，对流、涡动混合减弱，混合层深度不断减小。秋季，海面温度不断降低，对流、涡动混合加强，并且秋季也是风、浪开始增强的季节，综合因素作用，使混合层深度有不断加深的趋势。4月份混合层深度的大值区主要出现在北半球，而10月则主要分布在南半球，它们是冬、夏季混合层形成的过渡月份。

由上述分析可知，混合层深度和有效波高随季节的变化特征有较多的相似性，但在赤道地区，混合层深度在一年四季中都存着较大值，太平洋最为明显，而有效波高则全年一直较小。

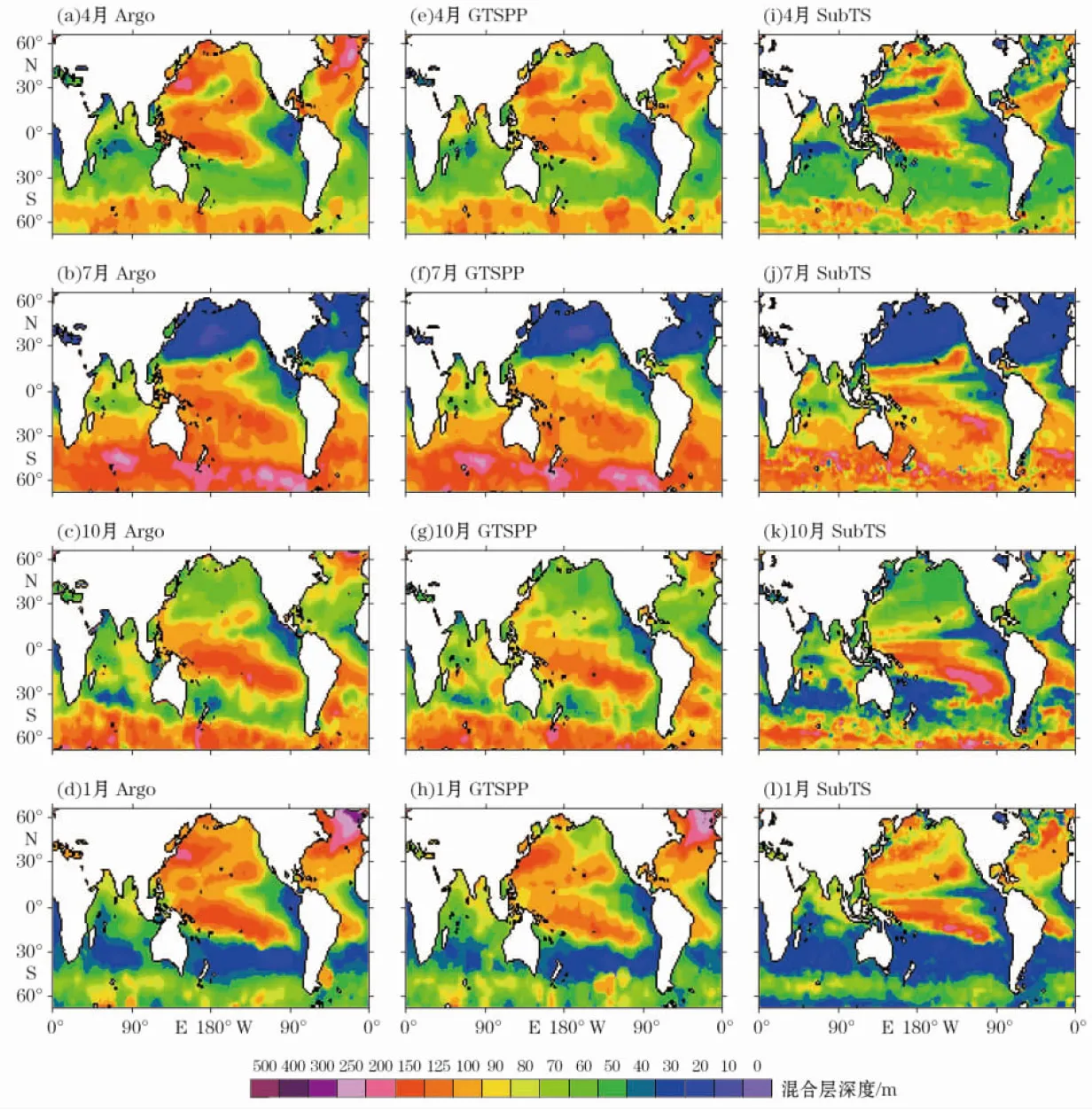
图3 月平均混合层深度的空间分布图

2.3 有效波高和混合层深度随时间变化

上面分析了有效波高和混合层深度的空间分布特征。为了进一步探讨二者随时间变化的一致性，图4～7分别给出了纬向平均、沿35°N、赤道和35°S断面上的有效波高和混合层深度随时间的变化。

混合层深度分布具有明显的季节变化和年际变化信号，这与有效波高随时间的分布特点相同。在北半球40°N左右和南半球50°S～60°S变化较强烈；赤道区域，有效波高一直较小，而混合层深度在赤道区域无明显年际和季节变化且一直保持较大值。在35°N纬线上，有效波高和混合层深度最大值出现在每年的一月份，35°S纬线上，有效波高和混合层深度全年最大值在7月份；赤道地区，有效波高没有明显的季节变化，年际变化信号较弱，混合层深度在赤道区域一直保持较大值，季节变化及年际变化特征也不明显。

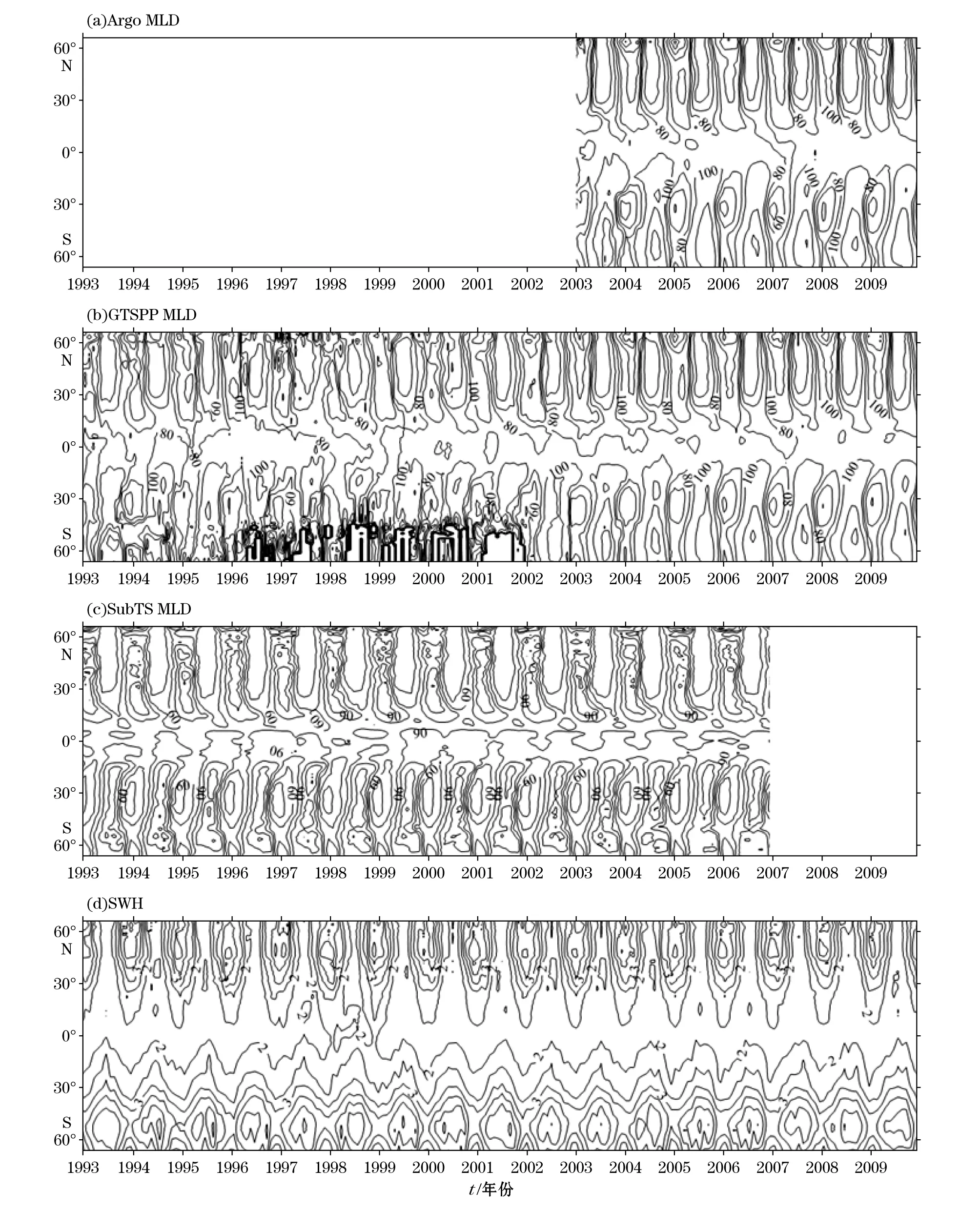
图4 纬向平均混合层深度(m)和有效波高(m)的时间序列

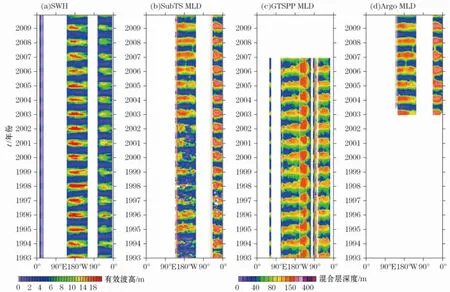
图5 沿35°N断面有效波高和混合层深度的时间序列图

图6 沿赤道断面有效波高和混合层深度的时间序列

图7 沿35°S断面有效波高和混合层深度的时间序列

混合层深度纬向平均和沿纬线随时间的分布图显示：SubTS数据得到的混合层深度随时间的分布变化较前两套数据年际变化更明显、稳定，杂乱信号较少；而Argo和GTSPP数据得到的混合层深度在某些区域空白，即这些区域的温度剖面数据不足，特别是GTSPP数据虽然时间序列比较长，但是在2005年之前的高纬度地区数据量一直很少，Argo数据也呈现类似情况，直到2005年之后由于Argo数据的增加才使得这两套数据基本覆盖全球。虽空白区域可经过插值处理进行填充，但却影响结果的可信度，而SubTS数据有覆盖范围广、网格规则、时间序列较长和广为接受等的特点，是下面对混合层深度和有效波高做相关性分析较好的选择。另外，由于垂向分层的不同，3套数据提取的混合层深度不完全一致。

综上所述，在赤道地区，有效波高和混合层深度随时间的分布变化较杂乱，但在中、高纬地区有效波高和混合层深度都有明显季节及年际变化规律，且对应性较好，其信号周期较为一致。

3 相关性分析

以上分析了海浪和混合层深度的空间变化特征及随时间的演变规律，通过比较Argo、GTSPP和SubTS温度数据的特点，选择SubTS数据进行混合层深度和海浪的相关性分析。以下将分别分析有效波高平方值和混合层深度的直接相关、距平及年际距平的相关性。为了考察二者的相对变化关系，计算相关系数时考虑了有效波高平方值和混合层深度同步相关和滞后相关。风场是上层海洋的主要驱动力之一，将大量能量输入给海洋，为了探究混合层变化的原因，同时分析了风场与混合层深度的相关性。

3.1 混合层深度与有效波高及风场的直接相关性分析

有效波高平方值和混合层深度直接相关的空间分布特征与前面分析的二者的时空变化规律一致。图8中，黑色等值线是相关系数为0的等值线，赤道地区有效波高平方值和混合层深度按时间的变化信号较杂乱(图6)，此区域的相关系数大部分也在零线以内，表明海浪和混合层深度在赤道附近相关程度低甚至呈负相关；随着南、北纬度的增大，二者的相关系数变大，大值区覆盖了南、北半球中高纬度的大部分区域，最大值达0.8以上，海浪和混合层深度的相关程度较高。相关系数的纬向平均在赤道附近最小，从赤道向南北纬不断增大，在高纬度地区又有所减小，几乎以赤道为轴线南北对称，并且北半球二者的相关性大于南半球。

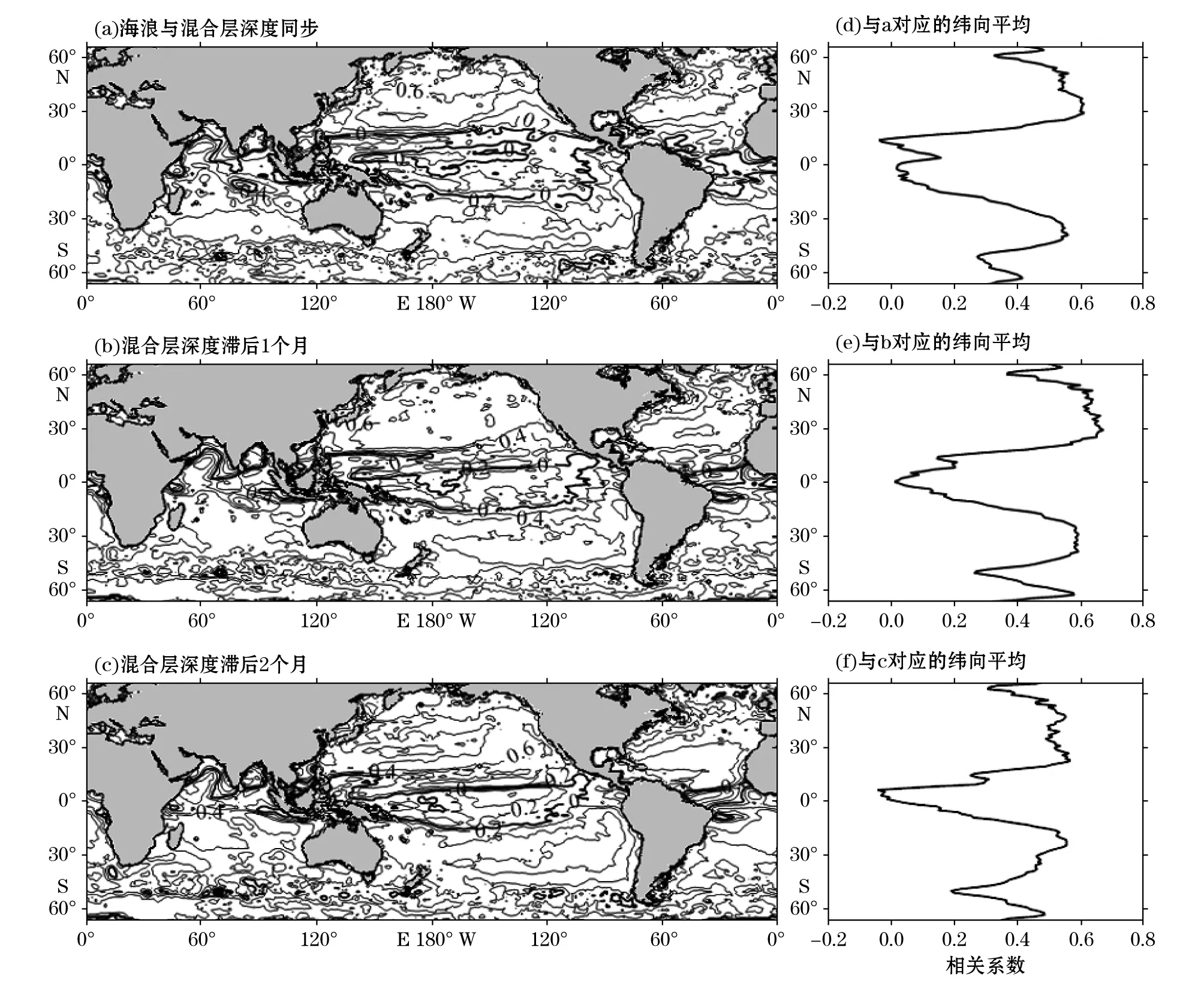
图8 海浪和混合层深度直接相关系数的空间分布及纬向平均

范聪慧[17]通过数值模拟的方式研究了多因素对海洋上混合层深度的影响，证明了风场的作用对混合层深度的变化较为敏感。为了探究海浪在混合层深度变化中所起的作用，我们又计算了风场与混合层深度的相关系数(图9)，风场与混合层深度直接相关系数的空间分布结构与前者相似，但明显小于有效波高平方值与混合层深度的相关系数，并且其纬向平均没有南北对称的特点。风应力首先将能量由大气输入给海浪，海浪对风的响应时间同步且较为敏感，海浪再通过自身搅拌混合的动力过程进一步影响混合层深度的变化，这也是造成混合层变化的原因之一。

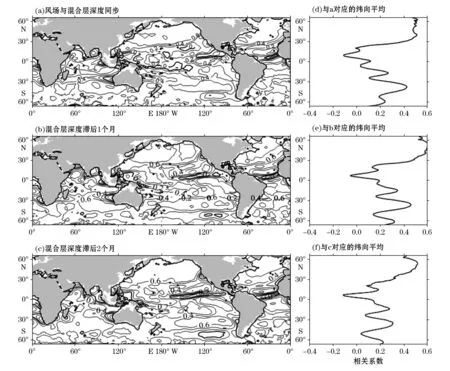
图9 风场和混合层深度直接相关系数的空间分布及纬向平均

比较3个不同对应时间的直接相关系数可以看出，当混合层深度滞后1个月时，混合层深度与海浪及风场的相关系数大值区覆盖范围最大，特别是北太平洋最为明显。

3.2 有效波高平方值与混合层深度距平的相关性分析

考虑到年周期的变化是海浪和海洋混合层变化的部分，我们将代表年周期的气候态月平均场减掉作为距平。绘制了混合层深度与有效波高平方值距平相关系数的空间分布(图10)并和混合层深度与风场的距平相关系数做了比较(图11)。

图10 海浪和混合层深度距平相关系数的空间分布及纬向平均

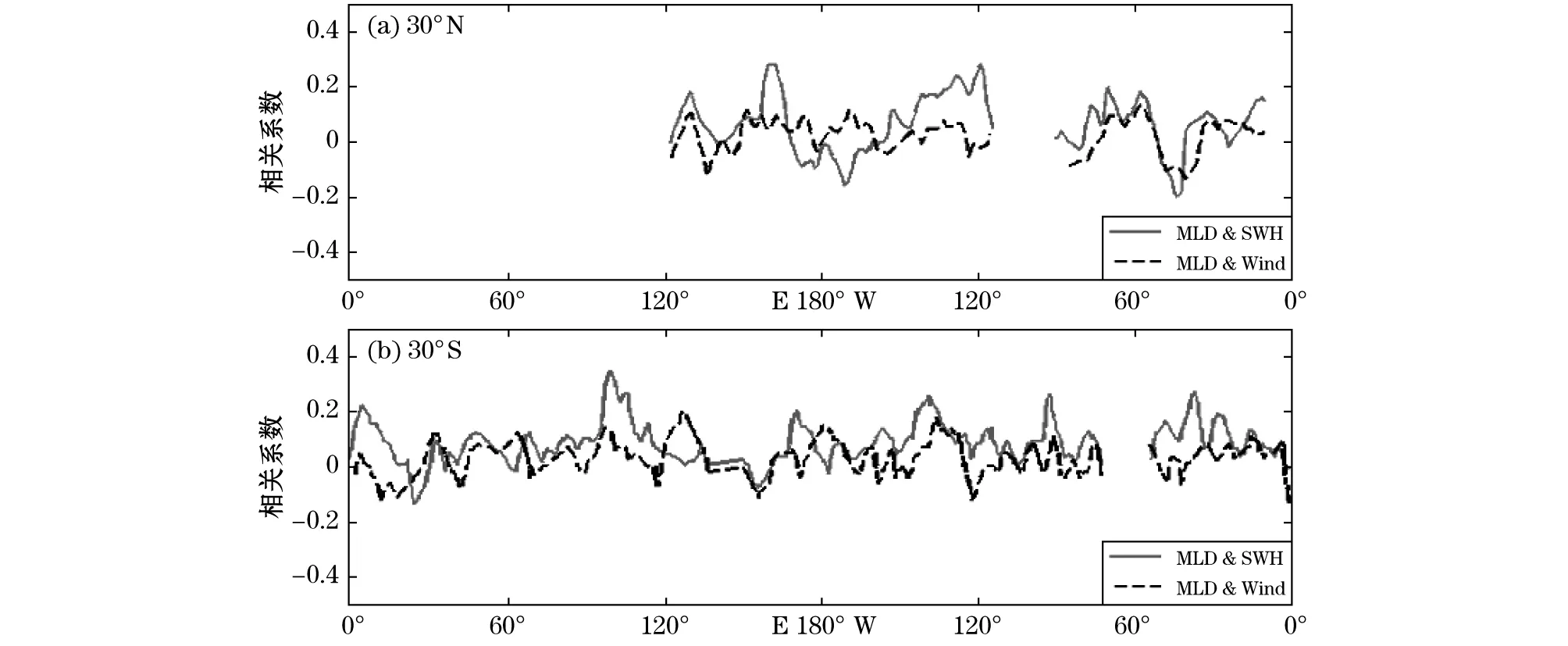
图11 混合层深度与风速和海浪距平相关系数的对比

海浪与混合层深度距平的相关系数在太平洋东部及南太平洋、南印度洋较大，最大值为0.6，但在赤道地区较小，相关性不显著；风场与混合层深度的距平相关系数全场普遍较小，并没有明显的大值区。比较30°N、30°S纬线上混合层深度与海浪及风场的距平相关系数，在大部分位置点上，混合层深度与有效波高平方值的距平相关系数较大且30°S纬线上更明显。

3.3 有效波高平方值与混合层深度年际距平的相关性分析

年际距平即当年的变量值减去前一年的变量值，如2002年有效波高的年际距平是2002年有效波高减去2001年，它反映了一个年际变化的高频分量[18]。常用变量的距平反映了其异常情况，但距平是相对于某个时间段平均的异常值，因此随时间段选取的不同，同一年变量距平的符号及大小都有可能不同。用距平来计算相关系数时，就难免受到数据时间段选取的影响。因此，本文进一步计算了混合层深度与海浪年际距平的相关系数(图12)同时也与风场与混合层深度年际距平相关系数做比较(图13)。

图12 海浪和混合层深度年际距平相关系数的空间分布及纬向平均

混合层深度与海浪年际距平相关性与其距平相关性的分析结果大致相同，其特点及大值分布区域与距平相关系数的结果对应；从图13看出，海浪与混合层深度的年际距平相关系数明显的大于风场与混合层深度的年际距平相关系数。

当混合层深度滞后一个月时，海浪与混合层深度的距平及年际距平的相关系数最大。比较混合层深度与海浪及风场的距平、年际距平的相关系数看出，风场与混合层的相关性整体上小于海浪与混合层深度的相关性，这也反映了海浪对混合层深度有更直接影响。与直接相关不同，混合层深度与海浪的距平、年际距平相关系数在太平洋东部、印度洋东部的大值很明显。Chen等[19]利用卫星资料发现了大洋东边界存在涌浪强化的现象，邓增安等[20]又进一步计算了太平洋东边界波浪输运，发现在太平洋东边界存在强烈的涌浪，这与有效波高与混合层深度的距平、年际距平相关系数的分布特点相吻合，这一区域盛行东南信风和东北信风，研究发现，风向和波浪输运方向存在很大的偏差，基本在90°左右，众所周知，风浪的平均方向与风向是一致的，这一区域二者方向差异较大，说明这一海域涌浪占优，而不是直接受当地风场影响的风浪，因此，我们有理由推测，相对于风场而言，这一海域的涌浪对海洋上混合层的影响更直接，因此二者的相关系数较大，但其物理过程及原因有待于探讨，内部机制也需进一步研究。

值得注意的是，混合层深度与海浪的直接相关、距平及年际距平的相关系数在赤道区域一直较小。赤道附近，全年太阳辐射强，大气向上层海洋输入热通量，对海洋上混合层起着直接加热的作用，加强了混合层内部的层化效果，而且此区域存在南、北赤道流、赤道逆流及赤道潜流，南、北赤道流与赤道逆流及赤道潜流方向相反，赤道逆流与北赤道流之间存在辐散上升运动，赤道潜流与南、北赤道流形成垂直剪切作用，这些海洋动力过程必然对赤道地区混合层深度的变化有一定的影响。赤道区域的海浪全年的变化一直很小，海浪不再是混合层深度变化的主导因素。

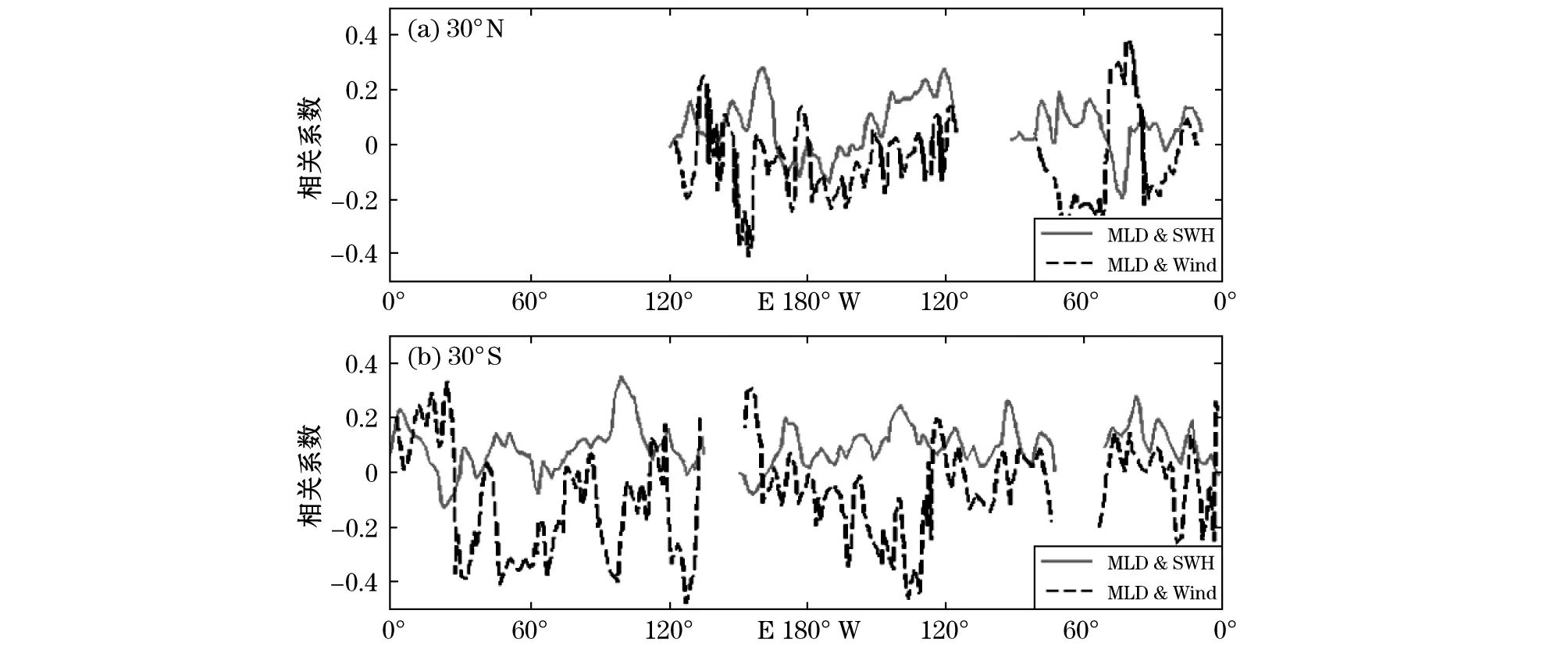
图13 混合层深度与风速和海浪年际矩平相关系数的对比

4 结 论

本文从海洋温度和海浪有效波高的观测数据出发，分析和探讨了海洋上混合层深度与海浪之间变化的相关性，得到如下结论：

1) 有效波高与混合层要素在直接相关中，除赤道区域及南大洋部分区域外二者相关性程度较高；距平及年际距平的相关性分析表明有效波高和混合层要素相关系数较大的区域主要分布太平洋的东边界及南印度洋的中纬度区域，有效波高和混合层要素存在着一定的相关性且在某些区域较为显著并且混合层深度的变化对海浪的响应有一定的滞后性。

2) 与风场相比，海浪作为大气向海洋输入能量的一种重要运动形式，它与混合层深度的直接相关、距平及年际距平的相关性均大于风场与混合层深度的相关性，是影响混合层深度变化的更直接的因素。海浪过程是风输入能量向次表层海洋传播的一个重要途径，但是二者间互相影响的内在机制还需要进一步深入研究。

致谢：Coriolis Argo资料中心提供的准实时Argo数据; NOAA 国际海洋数据中心(DODC)提供的GTSPP数据。

[1] WANG W, HUANG R X. Wind energy input to the Ekman layer[J]. Journal of Physical Oceanograph,2004a, 34(5): 1267-1275.

[2] WANG W, HUANG R X. Wind energy input to surface waves[J]. Journal of Physical Oceanograph,2004b, 34(5): 1276-1280.

[3] TENG Y, YANG Y Z, QIAO F L, et al. Energy budget of surface waves in the global ocean[J]. Acta Oceanologica Sinica,2009, 28(3):5-10.

[4] MAKIN V K，KUDRYAVTESEV V N. Coupled sea surface-atmosphere model:1.Wind over waves coupling[J]. Journal of Geophysical Research Oceans, 1999, 104:7613-7623.

[5] SUN Q. Numerical investigation of the effect of wave breaking on ocean surface mixed layer[D].Qingdao: The Ocean University of China, 2003.孙群.海浪破碎对海洋上混合层影响的数值研究[D].青岛：中国海洋大学，2003.

[6] YUAN Y L, QIAO F L, YIN X Q, et al. Analytical estimation of mixing coefficient induced by surface wave-generated turbulence based on the equilibrium solution of the second-order turbulence closure model[J]. Science China Earth Science,2013,56(1): 71-80.

[7] YANG Y Z, ZHAN R, TENG Y. Parameterization of ocean wave-induced mixing processes for finite water depth[J]. Acta Oceanologica Sinica,2009,28(4): 16-22.

[8] QIAO F L,YUAN Y L, YANG Y Z,et al. Wave induced mixing in the upper ocean: Distribution and application to global ocean circulation model[J]. Geophysical Research Letters,2004,31(11):293-317.

[9] WANG Y G, QIAO F L, FANG G H, et al. Application of wave-induced vertical mixing to the K profile parameterization scheme[J]. Journal of Geophysical Research, 2010,115(C9):703-710.

[10] CHEN H X, HUA F,YUAN Y L. Seasonal characteristics and temporal variations of ocean wave in the chinese offshore waters and adjacent sea area[J].Advances in marine science,2006,24(4):407-415.陈红霞，华锋，袁业立.中国近海及临近海域海浪的季节特征及其时间变化[J]. 海洋科学进展，2006, 24(4):407-415.

[11] CHEN Y D, ZHANG R, JIANG G R, et al. The type judge and characteristic analyses of the thermocline in the Pacific Ocean[C]∥Argo applied research papers. Beijing: Ocean Press,2006:204-214.陈奕德，张韧，蒋国荣，等．太平洋海域温跃层分类及其特征分析[C]∥Argo应用研究论文集,北京：海洋出版社，2006：204-214．

[12] SUN Z Y,LIU L,YU W D. Study on seasonal variations in the tropical indian ocean mixed layer depth derived from argo float data[J]. Advances In Marine Science,2007,25(3):280-288.孙振宇，刘琳，于卫东.基于Argo浮标的热带印度洋混合层深度季节变化研究[J].海洋科学进展，2007, 25(3): 280-288.

[13] LIU Y G. Satellite Oceanography[M].Beijing: Higher Education Press, 2009: 72-77.刘玉光.卫星海洋学[M].北京：高等教育出版社，2009: 72-77.

[14] Marine survey specification-Marine survey data processing:GB 12763.7-2007[S].Beijing: China Standard Press,2007.海洋调查规范-海洋调查资料交换:GB 12763.7-2007[S]．北京：中国标准出版社,2007.

[15] CRESSMAN G P.An operational objective analysis system[J].Monthly Weather Review,1959，87(10):367-374.

[16] WEI F Y. Modern climatic statistical diagnosis and prediction technology[M]. Beijing: Meteorological Press,1999:35-37. 魏凤英.现代气候统计诊断与预测技术.北京：气象出版社，1999: 35-37.

[17] FAN C H. Numerical simulation of the ocean surface mixed layer depth influenced by the multi-factors[D].Qingdao: Institute of Oceanology, Chinese Academy of Sciences,2007.范聪慧. 多因素对海洋上混合层深度影响的数值模拟[D].青岛：中国科学院海洋研究所，2007.

[18] FAN K, LIN M J,GAO Y Z. Predict the flood season precipitation of north China using annual increment method[J]. Since China,2008,38(11):1452-1459.范可，林美静，高煜中.用年际增量方法预测华北汛期降水[J].中国科学,2008, 38(11):1452-1459.

[19] CHEN G, CHAPRON B, EZRATY R, et al. A global view of swell and wind sea climate in the ocean by satellite altimeter and scatterometer[J].Journal of Atmospheric and Oceanic Technology, 2002, 19(11):1849-1859.

[20] DENG Z A,WU K J,YU T. The wave transport of the eastern area of the Pacific[J]. Acta Oceanologica Sinica, 2007,29(6):1-9. 邓增安，吴克俭，于婷.太平洋东边界波浪输运[J].海洋学报,2007,29(6):1-9.

Received: January 23, 2015

Correlation Analysis of the Waves and the Mixing Layer Depth Based on the Observation

SHI Yong-fang1, YIN Xun-qiang1，2, YANG Yong-zeng1，2

(1.TheFirstInstituteofOceanography,SOA, Qingdao 266061, China;2.LaboratoryofMarineScienceandNumericalmodeling,SOA, Qingdao 266061, China)

This study focused on the relationship between waves and the upper ocean mixing layer depth(MLD). Satellite altimeter observation data of significant wave height (SWH) and three sets of temperature observation data are used. An improved method is employed to obtain the ocean MLD. Both the spatial distribution and temporal variation of the monthly averaged SWH and MLD are analyzed and their correlationship is studied. Results indicated that correlation coefficient over both hemisphere mid-latitude regions is large, but small in equatorial regions. We filter monthly averaged climate state field that changes in annual periodicity, and get the anomaly correlation coefficient. While it is smaller in the equatorial region, in both eastern and southern Pacific Ocean and southern Indian Ocean, the anomaly correlation is significant. Furthermore, the annual anomaly correlation coefficient of SWH and MLD is also calculated. Its spatial characteristic is similar to the previous results. For studying the influence factors of mixing layer depth, the correlation coefficient of wind field and MLD are calculated. In conclusion, the study indicates that there is a certain correlation between ocean waves and upper ocean MLD. The former plays an important role in reducing the latter, which mechanisms are to be further studied.

significant wave height; mixing layer depth; correlation analysis

2015-01-23

国家重点基础研究发展计划项目——亚洲区域海陆气相互作用机理及其在全球变化中的作用(2010CB950404)和中尺度涡旋在海洋混合中的作用研究(41106032)； 国家高技术研究发展计划项目——南海及周边海域风浪流耦合同化精细化数值预报与信息服务系统(2013AA09A506)；海洋可再生能源专项资金项目——波浪能重点开发利用区资源勘查和选划(OE-W01区块)(GHME2011ZC07)

石永芳(1987-),女,山东商河人,博士研究生,主要从事物理海洋学方面研究.E-mail:shiyf@fio.org.cn*

杨永增(1969-)，男，山东泰安人，研究员，博士，主要从事海浪变分同化、海浪对海水的搅拌混合作用方面研究.E-mail:yangyz@fio.org.cn

(李 燕 编辑)

P73

A

1671-6647(2016)01-0022-15

10.3969/j.issn.1671-6647.2016.01.003