地球运动类题目多元解题法浅析

周圣然

[摘要]地球运动是最近几年地理科高考必考的内容，但学生很难拿分，因为教材相关内容较少、较简单，同时题目灵活多变、新题层出不穷。若学生掌握多种解题方法，遇到题目能随机应变，就能提高解题的正确率。

[关键词]地理 地球运动 解题方法

[中图分类号] G633.55 [文献标识码] A [文章编号] 16746058（2016）250127

地球运动是最近几年地理科高考必考的内容，但学生很难拿分，因为教材相关内容较少、较简单，同时题目灵活多变、新题层出不穷。若学生掌握多种解题方法，遇到题目能随机应变，就能提高解题的正确率。以下是笔者总结的关于地球运动的一些常用解题方法。

一、估算法

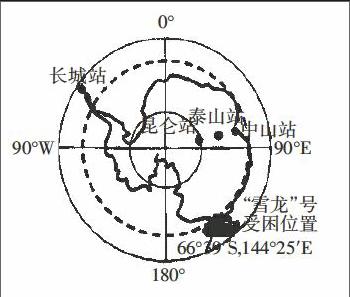
【例1】2013年11月第30次南极考察队乘“雪龙”号赴南极考察，并建立我国第四个南极科学考察站——泰山站（东经76°58′，南纬73°51′）。途中“雪龙”号获悉俄罗斯“绍卡利斯基院士”号客轮在南极被浮冰困住，随即赶往营救。读右边的南极轮廓图，结合所学知识分析： 2014年2月8日“泰山”站正式建成时，“泰山”站的昼夜长短状况和正午太阳高度是（B）

A. 极昼，正午太阳高度约28°

B. 昼长夜短，正午太阳高度约28°

C. 极昼，正午太阳高度约24°

D. 昼短夜长，正午太阳高度约24°

分析：由于该题是选择题，所谓选择题就是寻找最佳答案，我们就可以用估算法。太阳直射点由南回归线移至赤道，太阳直射点跨纬度23.5°，所花时间大约为90天，太阳直射点大约每天移动0.26°，而12月22日到2月8日大概有48天，则相差纬度为12.5°，所以2月8日太阳直射点的纬度大约是11°S，该日的正午太阳高度角大约是28°。

小结：由于相邻的两个两分两至日，时间相隔大约是90天，太阳直射点移动的纬度大约是23.5°，所以地球公转移动的纬度每天大约是0.26°，或者太阳直射点移动1°所花的时间大约是3.8天。此类估算法可以求任何一天太阳直射点的大概纬度，也可以求太阳直射点在某纬度时大概的日期。

二、排除法

【例2】某地在一年中T1、T2两个日期的正午太阳高度均为70°，且昼长T1日大于T2日，则（C）

A.该地可能位于赤道 B.该地可能位于6°S

C.T1可能是夏至日D.T2可能是秋分日

分析：如果该地位于赤道，则一年中可以有两个不同的日期，正午太阳高度角为70°，但赤道上的昼长是全年等长的，不可能存在昼长T1日大于T2日的现象，故A选项错误；该地为6°S，当该地正午太阳高度角为70°时，根据正午太阳高度角的计算公式：H=90°-|Φ-δ|，直射点的纬度为14°N，根据估算法日期大概是5月13日和8月1日附近，但此两日的昼长是相等的，故B选项错误；若T2为秋分日，根据正午太阳高度角的计算公式可得，该地为20°N或20°S，同理可推知T1日为春分日，则昼长T1=T2，与题意不符，故也错误。

小结：①23.5°N—90°N或23.5°S—90°S：一年中有两次正午太阳高度角相等且昼长相等。23.5°N—23.5°S：一年中有3次或4次正午太阳高度角相等，昼长可以相等，也可以不等。②一年中正午太阳高度角为70°，且昼长不等，则该地位于3.5°N—3.5°S之间，不包括赤道。③一年中正午太阳高度角为70°，且昼长不等，从直射点的纬度范围看：根据正午太阳高度角的计算公式可得，直射点的纬度范围是16.5°N—23.5°N或16.5°S—23.5°S，用估算法可知，当太阳直射点位于北纬或南纬16.5°时，日期大概是5月27日、7月18日、11月27日和1月17日。

三、规律法

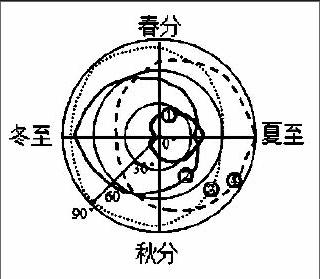
【例3】右图为不同纬度四地正午太阳高度季节变化分布图。有关说法正确的是（D）

A.纬度由高到低：①④③②

B.冬至日白昼时间由长到短：①②④③

C.夏至日日出由早到晚：①④③②

D.等长树干年最长午影由长到短：①②④③

分析：由题意可知，图中①地的正午太阳高度角，夏至日最大，冬至日最小且为0°，则该地纬度是66.5°N；图中②地的正午太阳高度角，冬至日最大且小于90°，夏至日最小且大于0°，则该地纬度为23.5°S—66.5°S；图中③地的正午太阳高度角有两次最大且为90°，都出现在冬半年，夏至日最小且为60°，则该地的纬度是6.5°S；图中④地的正午太阳高度角夏至日最大且为90°，则该地的纬度是23.5°N。所以四地的纬度由高到低的顺序为①②④③，故A选项错误；冬至日的昼长由长到短的顺序是②③④①，故B选项也错误；夏至日日出时间的早晚是由经度和纬度共同决定的，若四地经度不同，则不能判断，若四地经度相同，则日出由早到晚的顺序是①④③②，所以C选项也错误；年最长午影就是一年中正午太阳高度角最小时中午的影子，四地在一年中正午太阳高度角最小时的大小关系是③④②①，所以影子由长到短的顺序是①②④③，D选项正确。

小结：正午太阳高度角与纬度的关系，规律总结如下。①若一年中最大的太阳高度角为90°，则该地位于南北回归线之间。其中若最大只有一次且出现在夏至日，该地位于23.5°N；若最大只有一次且出现在冬至日，该地位于23.5°S；若最小的正午太阳高度角是66.5°，则该地位于赤道上。②若一年中最大的正午太阳高度角小于90°，最小的正午太阳高度角又大于0°，则该地位于回归线到极圈之间。其中若最大的正午太阳高度角出现在夏至日，则位于北半球；出现在冬至日，则位于南半球。③若一年中最小的正午太阳高度角小于或等于0°，表示该地会出现极夜现象，则该地位于极圈到极点之间。其中一年最大的正午太阳高度角若出现在夏至日，则为北半球；若出现在冬至日，则位于南半球。

四、概念法

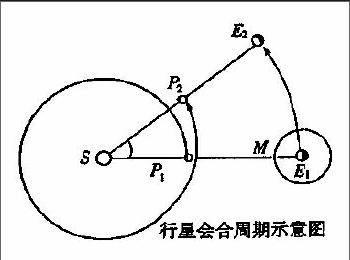
【例4】地球与其他行星都以不同的周期绕太阳公转，当行星和太阳都处地球的同一侧时，就是行星与太阳的会合，叫做行星合日，简称合。行星合日是一种周期性现象。根据行星会合周期示意图分析：若图中行星P的公转周期为P，地球的公转周期为E，则行星合日的周期T为 （D）

A. T=PE/ （P+E）

B. T= （E-P）/（E+P ）

C. T=PE/ （P-E）

D. T=PE/ （E-P）

分析：该题难度很大，但如果学生真正搞清楚线速度的概念，并从次概念入手去思考，还是可以做出来的。线速度的一般定义是质点（或物体上各点）做曲线运动（包括圆周运动）时所具有的即时速度。在地理上，线速度是地球自转时，某一点过一小时走的距离。此路程为转过的弧长，又可以看成是转过的角度。（因为转过的角度越大，弧长就越长。）设行星的公转速度为VP，则VP=360°÷P。设地球的公转速度为VE，则VE=360°÷E。根据题意，行星合日的周期为T，且若地球公转的角度为A，则行星公转的角度为A+360°。可以得出：360°+T*360°÷E= T*360°÷P。经过变形可得：PE=T（E-P），所以答案是D。

小结：有些看似非常难的题目，可能初看没有任何头绪，可以试着从概念入手，想想相关概念的意思，以及是怎么表达的，可能会出现意想不到的解题思路。

地球运动类题目对学生地图感知、逻辑思维等的要求是非常高的，教师在平时的教学中应该更加注重对学生读图析图、逻辑推导、创新解题方面能力的培养。任何题目都有解题的方法和步骤，也有解题突破口，只要仔细阅读题目，找出全部已知条件，并用不同方法尝试解答，一定能找到答案。

（责任编辑 周侯辰）