基于分形的自然景物模拟及仿真

牛亚群

太原学院基础部(太原 030032)

基于分形的自然景物模拟及仿真

牛亚群

太原学院基础部(太原 030032)

介绍了分形理论的发展过程，阐述了迭代函数系统(IFS)的基本原理。利用IFS随机迭代算法，采用Matlab软件仿真，较好的模拟了自然景物，验证了分形几何理论。

分形理论；迭代函数系统；Matlab软件仿真；自然景物模拟

分形理论是一种数学抽象，是自然界和社会的生活生产过程中的不完全规则事物高度概括。20世纪70年代，分形理论被首次提出，随着周边学科如计算机技术、网络技术、计算机图形学的成熟，已经成为一门重要的新学科，在很多应用领域得到很好的验证和推广，成为当今国际上许多学科的前沿研究课题之一。

分形理论在很多的基础学科和交叉学科领域有了很重大的突破，对促进整体科学技术的推进和发展，促进学科融合起着重要的作用。

随着计算机软硬件技术的提升，分形理论很好的应用到了计算机对现实世界的模拟，尤其在不规则事物模拟上有了很大的突破。过去很多受到计算机内存、CPU和显卡条件限制的分形理论实验随着计算机软硬件设备的不断攀登和发展均得到了长足进展。因此，本文以自然景物模拟为切入点，开展分形理论的实验研究。

1 分形理论

1975年，美籍法国数学家Mandelbrot最先创用了分形理论。他通过这个词来描述一大类复杂不规则的几何对象。分形(fractal)一词源于拉丁文fractus，本意是指“破碎的”、“产生不规则碎片”、“分数”等。分形理论目前还没有严格的数学定义，只能给出描述性的概念。粗略的说，分形是没有明确特征标度大自然本身描绘的曲线，其自相似性是统计数据抽象得来，并且，自相似性只存在于“无标度区间”[1]。

1904年，VonKoch通过初等方法构造了Von Koch曲线。该曲线的性质的最主要特征是处处不可微，该曲线是第一个发现的人为构造的局部与整体相似结构的曲线[2]。

得到Von Koch曲线的步骤如下：

设B0是平面A上的单位线段，将B0三等分。利用中间的1/3线段做出正三角形，新生成其他两个边。此时得到一个由4个长度为1/3的边所组成的连续折线，称此折线为B1，并称B1是由B0繁衍生成的.

分别对B1的每一条边都进行步骤1定义的规则变化，变化完成后可以得到由42个长度为1/32的边组成的连续折线，记其为B2。

按照规则逐次迭代，可以从折线序列B0,B1,B2,...,Bn,得到有限精度的极限曲线，即为Von Koch曲线。

如下图1所示即为Von Koch曲线的迭代过程。

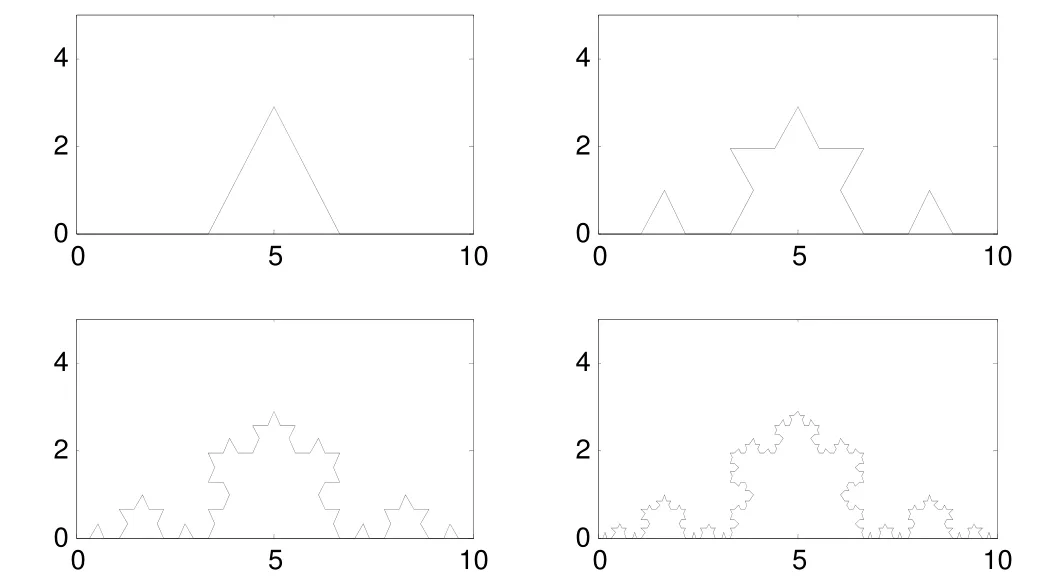
图1 逐步迭代的Von Koch曲线

2 线性IFS随机迭代算法

迭代函数系统又称为线性迭代表达式，函数系统中的每个迭代函数表达式都是线性的。在线性迭代函数的迭代中，采用如下的迭代算法：

(1)设定一个起始点(x0，y0)及总的迭代步数;

(2)以概率pk(k=1,2,3,…,N)选取仿射变换Wk,Wk形式为:

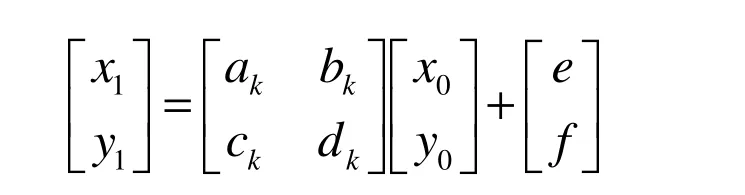
(3)以Wk作用点(x0,y0),得到新坐标(x1,y1);

(5)在屏幕上打出(x0,y0);

(6)重返第(2)步,进行下一次的迭代,直到迭代次数大于总步数为止.

在迭代算法中,Wk(k=1,2,3,…,N)是一组收缩仿射变换,式(2)称为线性IFS迭代表达式.

3 基于MATLAB的自然景物中树的模拟

由于分形几何的特点，使其理论在自然景物的模拟方面具有很好的模拟效果。云、山、水、树等自然景物通过计算机程序能够较好的模拟，见图2所示。

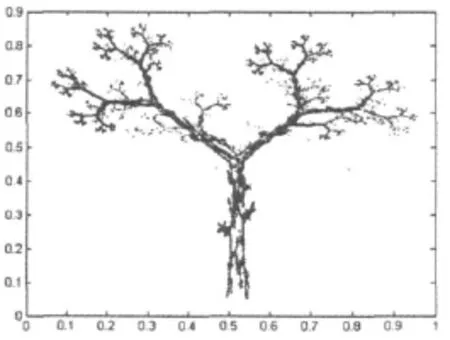
图2 树的模拟

通过对自然景物模拟问题算法的分析和求解,利用MATLAB矩阵工具中的模型语言算法去解决自然景物模拟过程中中的模拟和收敛问题[3]。MATLAB矩阵工具作为通用计算和模型求解的的良好平台，有着强大的数学计算能力和丰富的编程接口，对自然景物模拟求解问题有着很好的解决手段，对分形理论的应用和改进有着重要的科学价值。因此，MATLAB工具已经在分形理论自然物仿真模拟领域中选择为标准的问题求解软件工具之一。

MATLAB是强大的矩阵工具，在自然景物模拟领域中的问题求解中有着广泛的应用，其特点是对复杂的模型问题可以很好的分解、输入、分析和求解，程序执行速度快。MATLAB矩阵生成器提供了模型库，用户只需要很好的建立问题模型的相关数值和约束条件，利用此工具的演算，就可以得到问题的最优解。开发者只需通过建立的约束或目标函数，键入相应的数值，就可以对问题进行求解。MATLAB矩阵工具作为通用计算和线性求解的的基础平台，工具有着强大的数学计算能力和丰富的编程接口，还提供了科学算法的开发语言-M语言。掌握MATLAB矩阵工具，使用其中的M语言是可以使较大规模问题的输入过程和求解过程得到简化[4]。

利用MATLAB进行模型算法的优化设计可以很好的对自然景物模拟问题进行求解。优化求解的过程，计算方法简单,避免了人工输入大量的变量和约束条件,降低了时间复杂度，从而大大提高计算的准确性和程序执行速度[5]。

模拟初始数据如表1所示。

由此可见，利用Matlab对自然景物进行编程和分形模拟，具有一些优势。其条件设置简单、容易实现，而且，在相同硬件设置条件下比其他的程序语言具有更好的收敛速度和更快的生成速度.

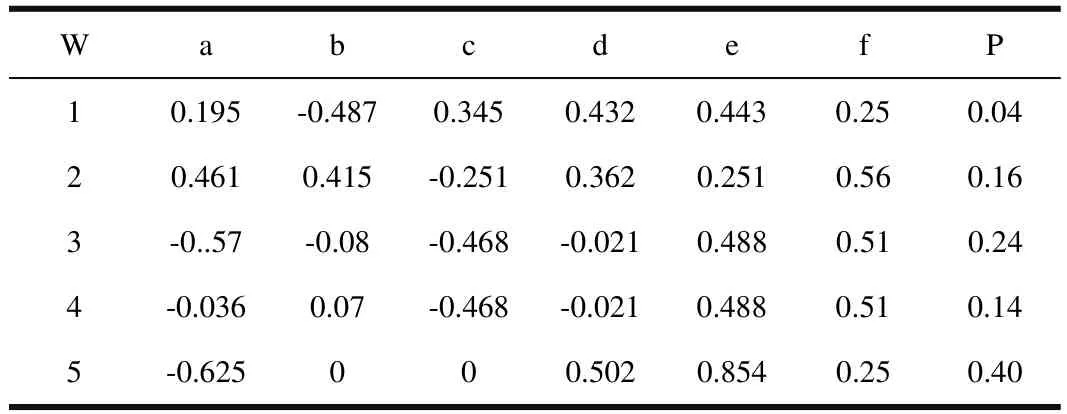
表1 模拟初始数据

4 结语

采用计算机技术对自然景物进行建模与仿真，可以在人类的生产生活中提供很多的便利，为物质财富的增加和精神世界的丰富提供了更多的实现手段。对自然景观进行模拟，可以促进一部分传统产业的发展，特别是在互联网服务提供商、医疗、旅游、教育和学习领域，自然景物模拟都能发挥重要的作用。因此，在基于分形的自然景物模拟和仿真在研究领域具有深入挖掘的价值。

通过分形理论相关文献的研究和对迭代函数系统(IFS)的基本原理的阐述解读，采用IFS随机迭代算法，利用Matlab软件进行编程和仿真,较好的模拟了自然景物中树的构造和图像图形，验证了分形几何理论，具有一定的实用价值。

[1]李彤,夏张莉,宿伟玲.求解丢番图方程的模拟植物生长算法[J].中国管理科学.2012,(S1).

[2]唐卫东,李金忠,刘昌鑫,胡雪华,李萍萍,卢章平.虚拟植物模型及其构建方法研究综述[J].计算机应用研究.2012,(09).

[3]刘颖,罗岱,黄心渊.基于OSG的Speedtree植物模型绘制研究[J].计算机工程与设计.2012,(06).

(责任编辑：文婷)

G42

A

1003-3319(2016)04-00013-02

10.19469/j.cnki.1003-3319.2016.04.0013