论粒计算的基本要素层次及其空间模型

梁俊奇，孙胜利

(1.商丘师范学院 数学与信息科学学院，河南 商丘 476000； 2.商丘职业技术学院 计算机系，河南 商丘 476000)



论粒计算的基本要素层次及其空间模型

梁俊奇1，孙胜利2

(1.商丘师范学院 数学与信息科学学院，河南 商丘 476000； 2.商丘职业技术学院 计算机系，河南 商丘 476000)

为粒计算建立一个统一的通用模型框架，研究其基本要素及其层次关系模型.讨论粒计算的粒化处理、粒化求解、粒化思维三要素的数量刻画.分析认为，粒化思维是粒计算的主导思维，更符合认知本原论；粒化求解是粒计算的方法论，更是实践创新；粒化处理是粒计算的基础，更是人机交互的入口.

粒计算；基本要素；层次；空间模型

0 引言

1996年，美籍华人数学家林早阳(T.Y.Lin)在UC.Berkeley大学扎德教授(L.A.Zadeh)重点实验室做客座教授期间，扎德教授建议他以粒数学(Granular Mathematics)作为他的研究领域.为了限制这个研究的范畴，林早阳教授用粒计算(Granular Computing)这个术语来标记此项研究领域，最初它被看成是粒数学的可计算部分. 扎德教授十分欣赏这个词,并且将它缩写成GrC，从此迅速发展成为今天的一个热门研究领域.

众所周知，信息粒广泛存在于我们的现实生活中，是对现实的一种抽象，信息粒化是人类处理和存储信息的一种反映.粒计算对人类的问题求解非常重要．它通过把复杂问题抽象、划分从而转化为若干较为简单的问题．粒计算是一种看待客观世界的世界观和方法论，有助于我们更好的分析和解决问题.

1 问题背景

目前，粒计算的主要模型有词计算模型、粗糙集模型、商空间模型.词计算模型(Computing with words)，就是用词语代替数进行计算及推理的方法，它的理论基础是模糊集合.尽管普通的精确方法(如数学)在某些科学领域应用相当广泛，也一直尝试着应用到人文学科中.但是人们在长期的实践中，已经越来越清楚地认识到精确的方法应用到人文学科有很大的局限性．面对巨大而又复杂的人文学科系统，区别于传统方法的新方法——模糊计算方法被美国计算机和控制论专家扎德教授提出；所谓粗糙集模型(Rough set)，其本质思想是利用不可分辨关系来建立论域的一个划分，得到不区分的等价类，即不同属性粒度下的概念粒，从而建立一个近似空间．在近似空间上，用两个精确的集合(上近似集和下近似集)来逼近一个边界模糊的集合．一个对象属于某个集合的程度随着属性粒度的不同而有所变化，为了更好地刻画集合边界的模糊性，粗糙集理论被波兰学者Z.Pawlakg在1982年提出；所谓商空间模型(Quotient space)，是用一个三元组来表示，即(X，F，T)．其中，X是论域，F是属性集，T是X上的拓扑结构．当取粗粒度时，即给定一个等价关系R(或说一个划分)，得到一个对应于R的商集(记为[X])，它对应于三元组 ([X]，[F]，[T])，称之为对应于R的商空间．商空间理论就是研究各商空间之间的关系、各商空间的合成、分解和在商空间中的推理. 商空间理论是我国学者清华大学教授张钹院士和安徽大学张铃教授两兄弟共同创立的. 词计算模型、粗糙集模型、商空间模型，它们各有侧重，但又有许多联系.如何为粒计算建立一个统一的通用模型框架，是当前粒计算研究的一个难点.

针对这一研究热点，国际著名学者、加拿大里贾纳大学姚一豫教授(Y.Y.Yao)指出，粒计算是研究基于多层次粒结构的思维方式、问题求解方法、信息处理模式及其相关理论、技术和工具的学科[1]1-13.对粒计算的研究应该着眼于三个基本观点：哲学思想观点、方法论观点和计算模式观点.有鉴于此，笔者认为粒化思维方式、粒化问题求解和粒化信息处理是粒计算的三个基本要素.本文主要针对这三个基本要素的层次关系，从理论模型上给予粗浅的分析.

2 基本要素的层次关系

2.1 粒化思维是粒计算的主导思维更符合认知本原论

大家都知道，粒在现实世界中是客观存在的，也就是说客观世界的本质是粒化的.同时，由于人类在解决和处理大量复杂信息问题时，因能力有限而把信息按其各自特征或性能划分成若干较简单的“块”，人的主观世界也是粒化的.由此可知，粒化思维方式不仅是哲学的，更是符合认知本原论的，它是人类思维的基本方式.也就是说，粒计算遵循“粒化思维先于粒化操作、粒化思维高于粒化操作、粒化思维成于粒化操作”的逻辑准则.因此，粒化思维是粒计算的主导思维[2]89-93，[3]43-47.粒化思维属于宏观认知领域，具有方向性的指导意义.所以，粒化思维研究是抽象的，它是粒化求解和粒化处理的前提与保障.

2.2 粒化求解是粒计算的方法论更是实践创新

我们认为，粒化思维与哲学思想、认知本原有关，粒化求解与方法论、实践创新有关.粒化求解是一个逻辑化的思辩过程、模式化的创建过程.主要解决两个问题，一是构建问题的粒结构，这属于方法论，是一个逻辑化的思辩过程.方法论是指人们认识世界、改造世界的一般方式、方法所构成的学说或理论体系，它是从整体上对该学科研究方法的哲学思考.由于粒计算是研究基于多层次粒结构的思维方式，具有粒逻辑化、粒推理的思维过程，因此粒计算学科方法论就是指人们在研究基于粒及多层次结构解决问题的过程中所遵循的粒逻辑化、粒推理等方法论原则和体系.二是在粒结构中进行问题求解，这属于实践创新，是一个模式化的创建过程.粒计算学科方法论所拥有的粒逻辑化、粒推理等研究方法在粒计算学科创建过程中具有高度的创造性尝试.粒化求解属于宏观与微观认知的交汇领域，一方面致力于问题求解的方法、技术和工具的研究与开发，另一方面还要考虑粒计算方法的有效性、可靠性、准确性、简便性、价值性.

2.3 粒化处理是粒计算的基础更是人机交互的入口

信息处理是将数据转换为信息、信息加工、信息筛选的过程.粒化处理是指在粒化问题求解的指导下，通过建立计算模型，进行以计算为主的具体算法设计实现问题求解. 表示和处理是粒化处理的数学手段，所谓表示是对问题的本质和内部结构的描述，所谓处理是为问题的求解提供具体的过程和方法.粒化处理是粒计算的基础，建立计算模型是解决实际问题的切入点，是粒计算的一个重要研究分支.粒结构化信息处理，强调以计算机为主体的信息处理与以人为主体的信息处理的差别，并逐步缩小这种差别，达到人机对话、互补长短的目的.

3 基本要素的层次模型

在信息检索中，向量空间模型将每一个文献表示为多维空间中的一个点.Y.Y.Yao教授给出了一个三维空间模型[4]35-37，下面进一步给出三维空间模型的数量刻画.

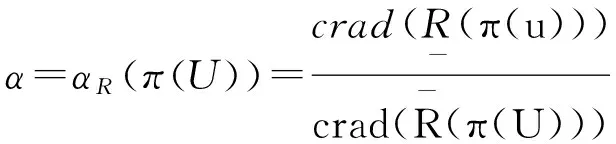
4 结语

粒计算是信息处理的一种新的概念和计算范式，覆盖了所有有关粒度的理论、方法、技术和工具的研究，主要用于处理不确定的、模糊的、不完整的和海量的信息.粗略地讲，一方面它是模糊信息粒度理论、粗糙集理论、商空间理论、区间计算等的超集，另一方面是粒数学的子集.具体地讲，凡是在分析问题和求解问题中，应用了分组、分类和聚类手段的一切理论与方法均属于粒计算的范畴.

[1] 苗夺谦，王国胤，刘 清.粒计算：过去、现在与展望[M].北京：科学出版社，2007.

[2] 李 鸿.粒计算的基本要素研究[J].计算机技术与发展，2009，19(11).

[3] 李 鸿.粒计算的四面体模型[J].计算机工程与应用，2009，45(28).

[4] 苗夺谦，李道国.粗糙集理论、算法与应用[M].北京：清华大学出版社，2008.

[责任编辑 梧桐雨]

The Basic Element Level and Spatial Model of Granular Computing

LIANG Junqi1, SUN Shengli2

(1.ShangqiuNormalUniversity,Shangqiu476000,China;2.ShangqiuPolytechnic,Shangqiu476000,China)

The paper established a unified framework for the general model of granular computing for studying its the basic elements and hierarchy model, and in the paper the quantitative characterization of granular computing granulation, granulation solution and granular thinking were discussed. Analysis showed that granular thinking——the grain leading thinking——is more in line with the cognitive principle; solution method of granular computing is the practice of innovation; granulation is a granular computing foundation and the entrance of human-computer interaction.

Granular Computing; basic elements; levels; space model

2016-07-20

河南省自然科学研究基金资助(项目编号：122300410222)；河南省教育厅自然科学研究基金资助(项目编号：2011A140007，2012B120011，2014A120008)

梁俊奇(1958- )，男，河南宁陵人，商丘师范学院教授，硕士生导师，主要从事智能计算与不确定信息处理研究。

1671-8127(2016)05-0011-03

TP18；O231

A