基于复调制细化谱分析的轧辊偏心谐波参数估计

徐翔宇,李海龙

(1.内蒙古科技大学信息工程学院,内蒙古包头 014010; 2.太原理工大学信息工程学院,山西太原 030000)



基于复调制细化谱分析的轧辊偏心谐波参数估计

徐翔宇1,李海龙2

(1.内蒙古科技大学信息工程学院,内蒙古包头 014010; 2.太原理工大学信息工程学院,山西太原 030000)

针对轧辊的上、下支撑辊偏心信号是密集型频谱的特点,提出了一种基于复调制细化谱分析方法的轧辊偏心谐波参数估计新方法.利用复调制细化谱分析方法准确估计出偏心谐波的频率及幅值;同时,结合快速傅里叶变换算法估计出偏心谐波的相角参数.仿真实验结果验证了该方法在偏心谐波参数估计上的有效性和可行性.

轧辊偏心谐波;复解析带通滤波器;频谱细化分析;参数估计

1 引言

轧辊偏心是轧制过程自动化中不可忽视的问题.轧辊偏心以上、下支撑辊偏心为主,并间接反映于可检测的轧制力信号中.通过轧制力信号的分析,提取出偏心信号参数是实施偏心主动补偿控制的前提.根据轧机上、下支撑辊的机械结构及运动特点[1],可知轧辊偏心信号属于密集型频谱的信号,即上、下支撑辊的偏心频率间隔很窄,而各次谐波之间的频带分布较宽.只考虑一个支撑辊的偏心时,快速傅里叶变换是一种较为有效的偏心信号分析方法[2,3],但因快速傅里叶变换(Fast Fourier Transform,FFT)算法自身的局限性,不能准确地估计出偏心信号的参数[4].同时,对于上、下支撑辊这种频谱密集的谐波,FFT算法还会因频谱干涉现象[5],导致参数估计精度进一步下降.降低采样频率或增加采样点数可在一定程度上提高FFT算法的精度,但是会产生频率分析范围变小及计算量增大等问题.

在工程信号分析中,对于具有密集型频谱的信号,通常采用频谱细化技术[6,7]进行分析.其中,复调制细化谱分析方法是最为有效的方法[8],但是存在细化倍数较低、计算量较大等缺点,采用基于复解析带通滤波器的复调制细化谱分析方法可以大大地提高细化倍数和运算速度.本文针对轧辊的上、下支撑辊偏心信号密集频谱特点,采用复解析带通滤波器的复调制细化频谱分析算法进行轧辊偏心信号参数估计,其分析精度、运行速度都远优于传统FFT算法.

2 偏心对厚度的影响及偏心参数模型

轧辊和轧辊轴承形状的不规则变化引起的周期性辊缝变化称为轧辊偏心,偏心包括工作辊偏心和支撑辊偏心.在一个机架中,每个轧辊的偏心量对合成轧辊偏心量e都有影响.因此,辊缝会随着轧辊旋转而发生变化.在有轧制力的情况下,由于轧辊偏心的存在而使辊缝减小时,将产生附加轧制力ΔPe,这个力将使轧机机座发生弹性形变ΔSe.液压机构刚度设为KH,可得偏心作用的物理模型,如图1所示.

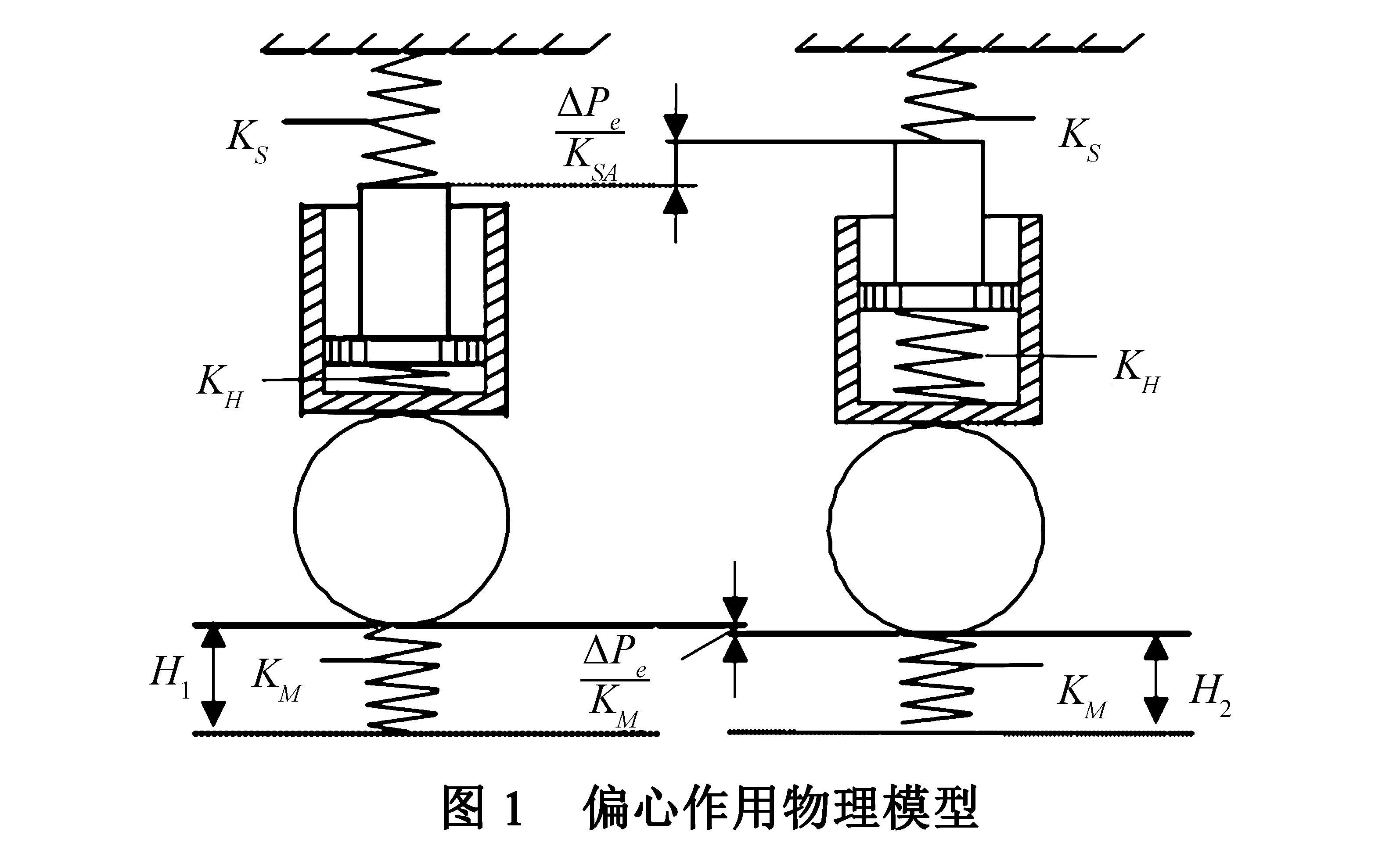
图1中,KS为轧机刚度、KM为轧件塑性系数、KSA为轧机有效刚度、H1、H2分别为轧辊偏心影响前、后的轧出厚度.轧辊偏心量e等于:

(1)

轧辊偏心、轧制力和轧件厚度的关系如图2所示,图中曲线1为理想轧辊偏心曲线,曲线2为轧机弹跳曲线,曲线3为轧件塑性曲线.

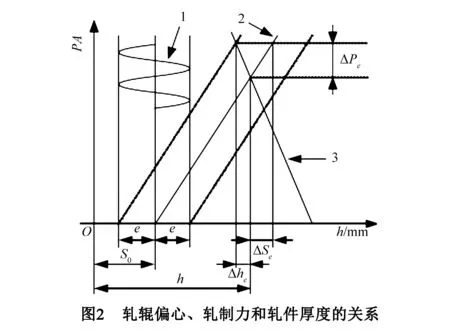
由图2可以看出,当有偏心e存在使原空载辊缝S0减小时,实际板厚减少了Δhe,但由于同时轧制力增大,压力AGC控制系统会认为此时带材入口厚度增大了ΔSe,因而在控制器的作用下系统朝着使板厚减少的方向调整压下,其结果是使带材厚差加大,调节质量恶化.

由于支撑辊的辊径较工作辊的辊径大,且换辊周期也较长,因此在线工作时,支撑辊偏心比工作辊偏心严重.由于上、下支撑辊辊径不同,且存在一定的转速差,此时的轧辊偏心信号模型必然包含两个支撑辊的偏心,由于偏心信号基波和二次谐波的幅值较大,因此偏心信号模型可以表示为:

(2)

式中:y(t)为偏心信号;fAi、fBi分别为上、下支撑辊偏心的第i次谐波频率值;Ai、Bi分别为上、下支撑辊偏心的第i次谐波分量的幅值;φAi、φBi分别为对应的初相角;η(n)为随机噪声项.

因此,对测量得到的轧制力信号进行分析,提取得到轧辊偏心信号的上述三个参数,就可以建立精确的偏心补偿模型.

3 基于复调制细化谱分析的轧辊偏心参数估计

3.1 复解析带通滤波器

根据复解析带通滤波器的理想幅频特性如图3所示,其中π对应采样频率fs的一半,通带宽为ω2-ω1,ωe为带通的中心频率.为了得到图3的解析带通滤波器,先作一个实低通滤波器,其幅频特性如图4所示,其中低通滤波器截止频率为

(3)

其冲激响应函数为

(4)

再对低通滤波器进行复移频,将其通带的中心由0移至ωe,即可得到图3所示的复解析滤波器,其冲激响应为复指数序列:

h(k)=hl(k)ejkωe=hl(k)[cos(kωe)+jsin(kωe)]

(5)

(6)

虚部为:

(7)

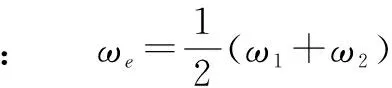
(8)

将式(3)和式(8)代入式(6)和式(7)得

(9)

(10)

3.2 复解析带通滤波器的复调制细化谱分析轧辊偏心参数估计

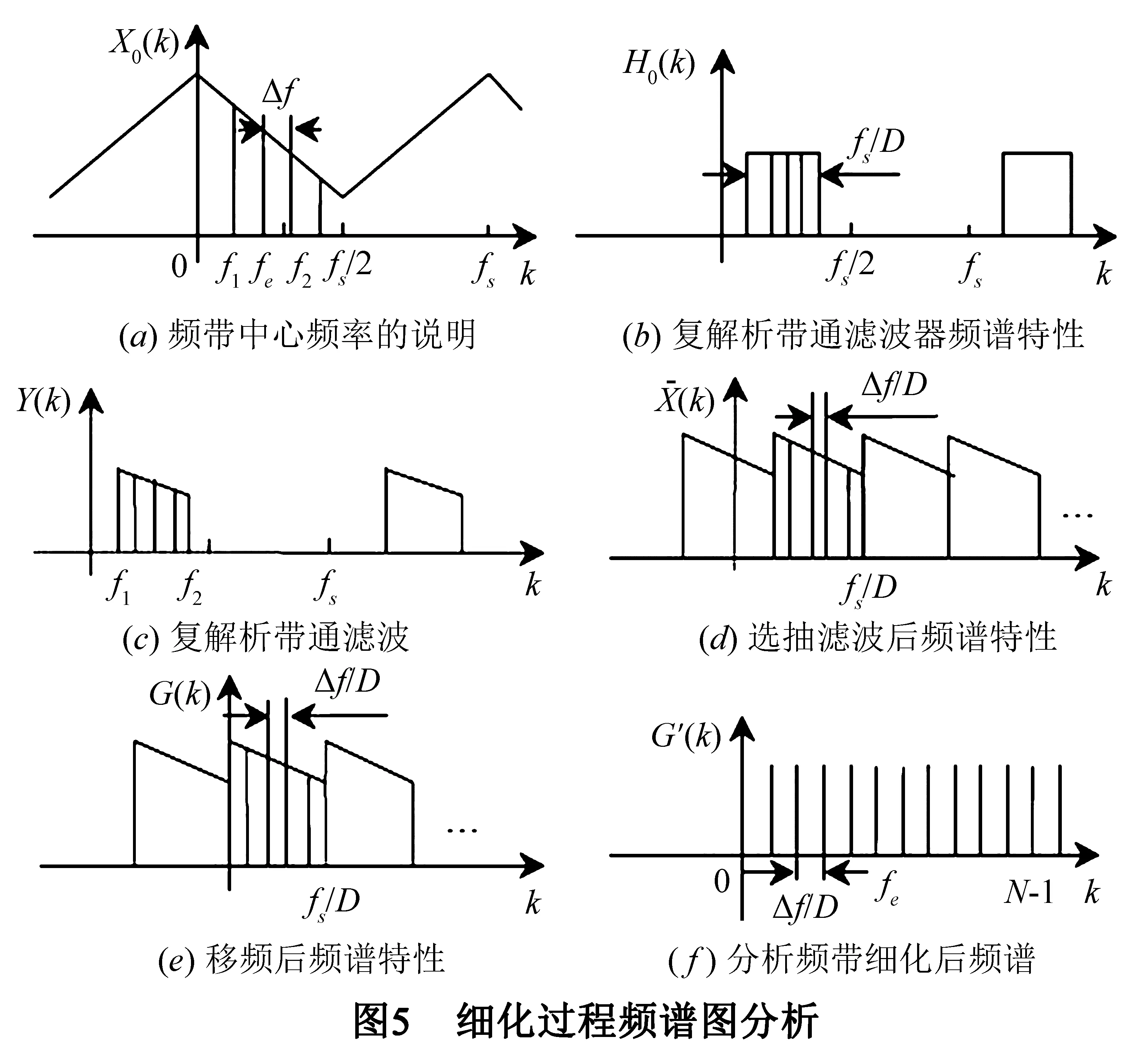
设采样频率为fs,对轧制力信号x(t)进行DN+2M点采样,得时间序列x0(n)(n=0,1,…,DN+2M),其中D为选抽比,M为滤波器半阶数,N为FFT分析点数.x0(n)的周期频谱为X0(k),频率间隔为Δf,如图5(a)所示.采用复解析带通滤波器的宽度为fs/D,隔D点选抽一点,然后移频并做N点谱分析,频带f1-f2用N条独立的谱线来表示.具体步骤如下[9]:

(1)确定分析频带的中心频率fε和选抽比D.设所分析的频带起始和截止频率为f1和f2,则中心频率为:

fε=(f1+f2)/2

(11)

由于复解析带通滤波器的带宽为fs/D,而分析频带的宽度为f1-f2,所以有fs/D=f1-f2,即

D=fs/(f1-f2)

(12)

(2)构造截止频率为fs/2D的实低通滤波器hL(n),并将hL(n)进行ωε=2fε的复调制移频得到复解析带通滤波器h(n),带宽为fs/D,其频谱特性如图5(b)所示.所构造带通滤波器的实部和虚部的具体表达式见式(9)和式(10)所示.图5(a)所示的信号频谱经复解析带通滤波器滤波后其频谱特性如图5(c)所示.

(13)

(14)

(5)FFT分析.对g(n)做N点FFT变换和谱分析,不需要进行频率调整就可以得到具有N条独立谱线的细化频谱,从中提取出偏心频率,其频谱如图5(f)所示.

4 复调制细化频谱分析的轧辊偏心参数估计

设轧机上、下支撑辊偏心信号的基波角频率分别为1Hz和1.03Hz[10],考虑二次谐波及测量噪声,建立如下理论偏心模型:

x(t)=0.1sin(2πt+0.2)

+0.08sin(2πt×1.03+1.1)

+0.05sin(2πt×2+0.8)

+0.04sin(2πt×2.06+1.6)

+n(t)

(15)

式中n(t)为噪声信号.

首先对偏心信号进行频率和幅值估计.分别采用FFT算法和复调制细化频谱分析算法对采样信号进行分析.图6为含有噪声的偏心信号.

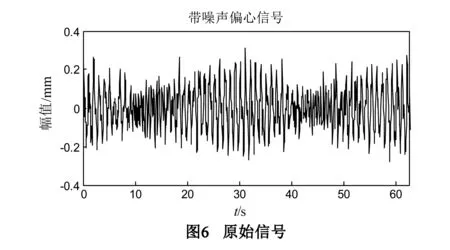
由于偏心模型中的1Hz、1.03Hz与2Hz、2.06Hz间隔较大由FFT法可以容易地分辨.但是1Hz和1.03Hz之间,2Hz和2.06Hz之间间隔较小需要使用本文方法分别细化.对1Hz和1.03Hz进行细化:设频带起始和截止频率分别f1=0.5Hz和f2=1.5Hz,采样频率fs=100Hz,采样点数N=1024,则由3.2小节中式(11)、(12)得中心频率fε=1Hz、选抽比D=100,由FFT法得到的频谱特性如图7.对2Hz和2.06Hz进行细化:设频带起始和截止频率分别为f1=1.5Hz和f2=3.5Hz,采样频率fs=200Hz,采样点数N=1024,得中心频率fε=2Hz、选抽比D=100,图8是复调制细化频谱分析算法的细化频谱特性图.由图7可以看出,FFT算法的分析结果因干涉效应和栅栏效应具有较大的幅值误差;由图8可以看出,复调制细化频谱分析算法对于具有密集频谱特点的支撑辊偏心信号有较高频率的分辨率和幅值精度.

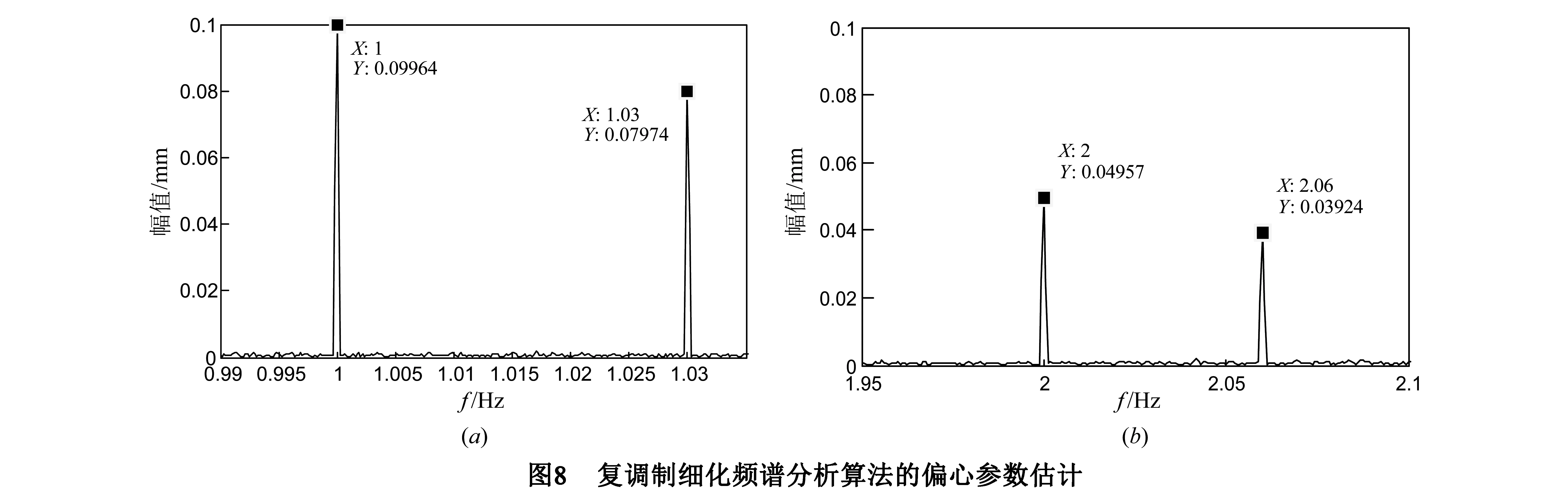
得到偏心信号的频率和幅值参数后,对上述偏心模型进行仿真得到偏心信号的相角估计值.这里采用FFT算法进行估计,结果如表1所示.

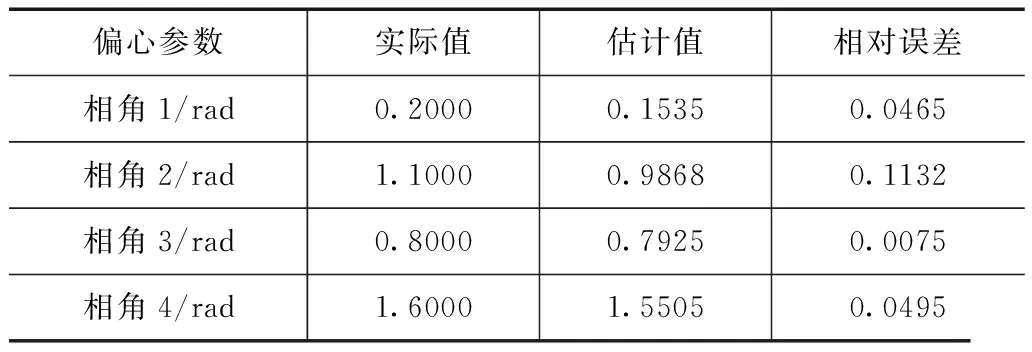
表1 偏心相角估计

5 实验验证

将上一小节复调制细化频谱分析算法的偏心信号参数辨识方法和FFT算法的参数辨识分别应用于压力AGC,进行偏心补偿控制研究.

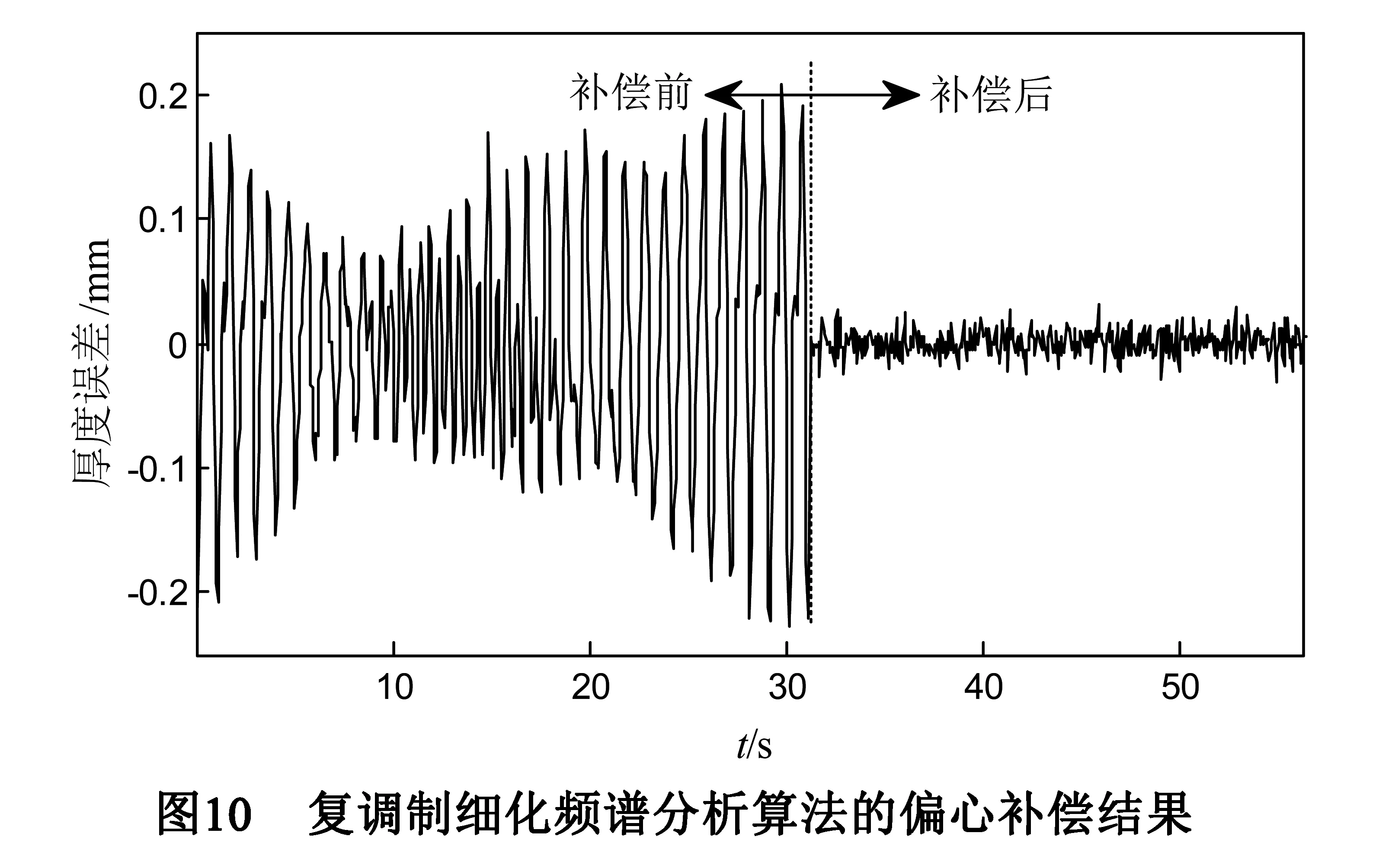
对实验室的二辊冷轧机进行实验.设备编号:20080834;设备型号:φ150/350*300;工作辊辊身最大直径为150mm,最小直径为105mm;支撑辊直径为350mm;工作辊身长:300mm;最大轧制速度:0～0.3m/s;最大轧制力:1200kN;传动比180∶1;主电机功率:18.5kW;投入基于FFT算法的轧辊偏心补偿装置前、后的出口带材厚度波动控制结果如图9所示,偏心引起的厚度波动减少了79%;对于基于复调制细化频谱分析算法的轧辊偏心补偿装置,其投入前、后的出口带材厚度波动控制结果如图10所示,偏心引起的厚度波动减少了87%.结果表明,本文提出的偏心信号参数估计方法精度相对较高,补偿效果优于FFT法.

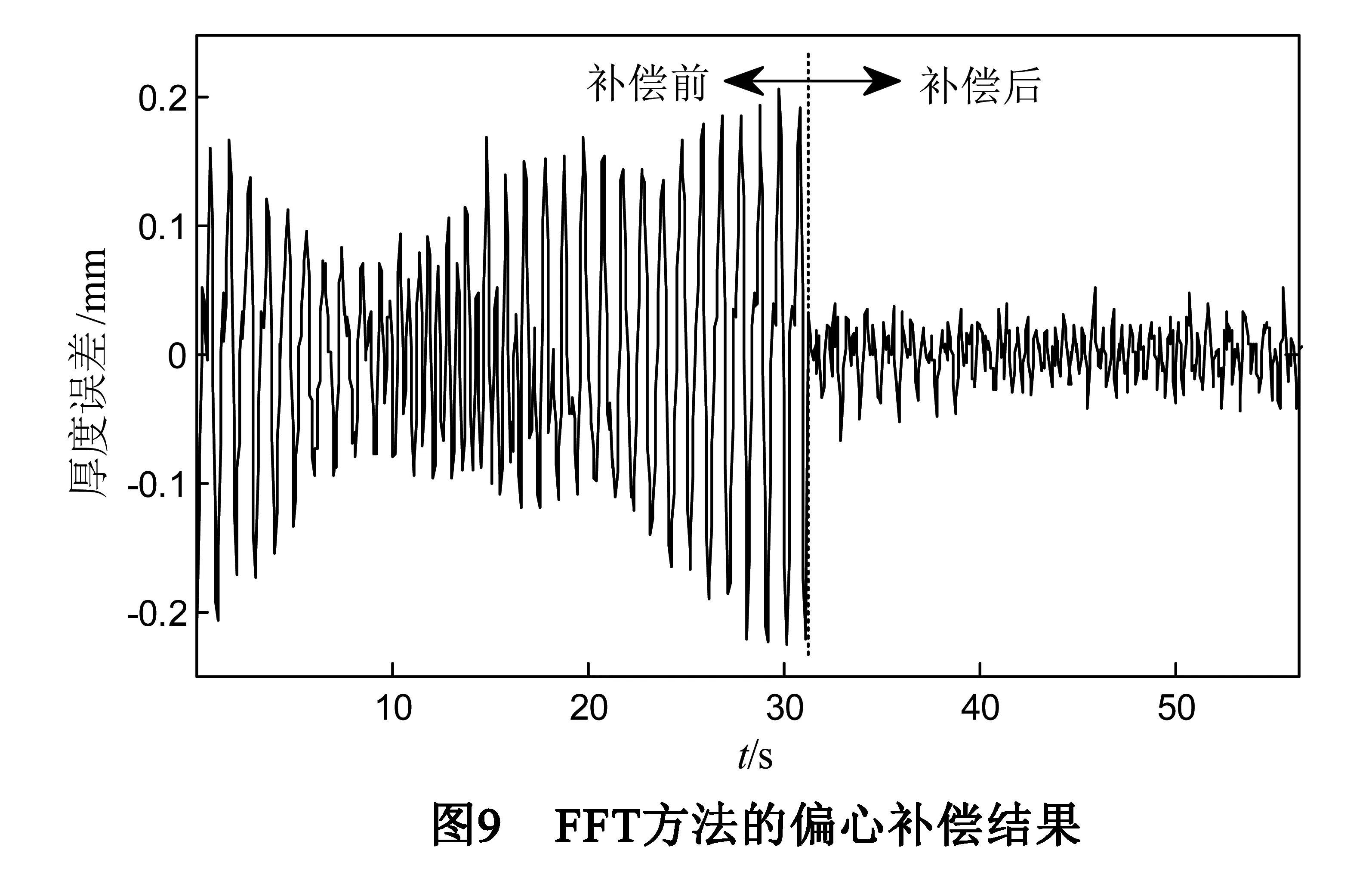
6 结论

针对轧辊上、下支撑辊偏心信号密集频谱的特点,以及FFT对轧辊偏心信号分析的局限性,本文提出了基于复解析带通滤波器的复调制细化谱分析方法的轧辊偏心参数谐波估计新方法.该方法非常适用于具有上、下支撑辊偏心这种密集频谱偏心信号参数的提取,仿真结果也验证方法的可行性和有效性,为轧辊偏心参数的准确提取提供了一个有效方法.

[1]李勇.板带轧机轧辊偏心控制的研究[D].沈阳:东北大学,2008.

Li Yong.Study on Roll Eccentricity Control for Flat Rolling Mill [D].Shenyang:Northestern University,2008.(in Chinese)

[2]李勇,等.轧辊偏心先进控制算法和实验研究[J].东北大学学报(自然科学版),2012,33(10):1440-1444.

Li Yong,et al.Advanced algorithm and experiment of roll eccentricity [J].Journal of Northeastern University (Natural Sience),2012,33(10):1440-1444.(in Chinese)

[3]龚超,等.基于FFT的快速高精度载波参数联合估计算法[J].电子学报,2010,38(4):766-770.

Gong Chao,et al.Rapid precision carrier parameter joint estimation algorithm based on FFT [J].Acta Electronica Sinica,2010,38(4):766-770.(in Chinese)

[4]牛满科,等.基于循环统计量的轧机偏心线性预测及补偿控制[J].北京科技大学学报,2009,31(12):1605-1610.

Niu Man-ke,et al.Linear prediction and compensation control of roll eccentricity based on cyclic statistics [J].Journal of University of Science and Technology Beijing,2009,31(12):1605-1610.(in Chinese)

[5]丁康,谢明,杨志坚.离散频谱分析校正理论与技术[M].北京:科学出版社,2008.100-111.

Ding Kang,Xie Ming,Yang Zhi-jian.The Theory and Technology of Discrete Spectrum Correction [M].Bejing:Science Press,2008.100-111.(in Chinese)

[6]丁康,朱小勇.适用于加各种窗的一种离散频谱相位差校正法[J].电子学报,2001,39(7):987-989.

Ding Kang,Zhu Xiao-yong.A discrete spectrum are applicable to all Windows and phase difference correction method [J].Acta Electronica Sinica,2001,39(7):987-989.(in Chinese)

[7]郝重阳,唐文彬,等.一种快速局部细化频谱分析新方法——SSA[J].电子学报,2000,28(3):106-108.

Hao Chong-yang,Tang Wen-bin,et al.A new method of rapid local refinement spectrum analysis-SSA [J].Acta Electronica Sinica,2000,28(3):106-108.(in Chinese)

[8]谢明,丁康.基于复解析带通滤波器的复调制细化谱分析的算法研究[J].振动工程学报,2002,15(4):479-483.

Xie M,Ding K.Algorithm of multiple modulation zoom spectrum analysis based on complex analytic band pass filter[J].Journal of Vibration Engineering,2002,15(4):479-483.(in Chinese)

[9]丁康,谢明,等.基于复解析带通滤波器的复调制细化谱分析原理和方法[J].振动工程学报,2001,14(1):29-35.

Ding Kang,Xie Ming,et al.Principle and method of multiple modulation zoom spectrum analysis based on multiple analytical band-pass filter [J].Journal of Vibration Engineering,2001,14(1):29-35.(in Chinese)

[10]王洪希,杨卫东,田伟.基于高阶累积量Root-MUSIC法和Prony法的轧辊偏心谐波参数估计[J].电子学报,2014,42(11):2213-2218.

Wang Hong-xi,Yang Wei-dong,Tian Wei.Roll eccentricity harmonic parameter estimation based on root-music of HOC and Prony method [J].Acta Electronica Sinica,2014,42(11):2213-2218.(in Chinese)

徐翔宇 女,1991年11月出生,内蒙古呼和浩特人.2013年进入内蒙古科技大学攻读硕士研究生,研究领域为控制理论与计算机控制、信号处理.

E-mail:291957826@qq.com

李海龙 男,1988年8月出生,内蒙古赤峰人.2013年进入太原理工大学攻读硕士,现为在读硕士生,研究领域是信号处理,检测技术与智能仪表.

E-mail:lihailong4855@163.com

Parameter Estimation Based on Multiple Modulation Zoom Spectrum Analysis Applied to Roller Eccentric Harmonic

XU Xiang-yu1,LI Hai-long2

(1.InformationEngineeringSchool,InnerMongoliaUniversityofScienceandTechnology,Baotou,InnerMongolia014010,China;2.InformationEngineeringSchool,TaiyuanUniversityofTechnology,Taiyuan,Shanxi030000,China)

For the roller eccentric signal of upper and lower support rolls is intensive spectrum.In this paper,a new roller eccentric harmonic parameter estimation method is presented,which is the harmonic parameter estimation based on multiple modulation zoom spectrum analysis.Using multiple modulation zoom spectrum analysis algorithm to accurately estimate the frequency and amplitude of eccentricity harmonics;At the same time,combined with the FFT (Fast Fourier Transform) algorithm to estimate phase parameters of the eccentric harmonic.The simulation results show that this method is effective and feasible for eccentric harmonic parameter estimation.

roll eccentric harmonic;multiple analytical band-pass filter;zoom spectrum analysis;parameter estimation

2015-02-03;

2015-12-22;责任编辑:孙瑶

TP273;TG333.17

A

0372-2112 (2016)10-2398-05

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.10.017