基于高阶统计量的L-DACS1系统自适应干扰消除技术研究

曾孝平,贺 渊,简 鑫,黄 杰,李梦如

(重庆大学通信工程学院,重庆 400030)



基于高阶统计量的L-DACS1系统自适应干扰消除技术研究

曾孝平,贺 渊,简 鑫,黄 杰,李梦如

(重庆大学通信工程学院,重庆 400030)

针对L-DACS1(L-band Digital Aeronautical Communication System Type 1)与DME(Distance Measuring Equipment)信号在时域、频域和低阶统计域干扰抑制不理想的问题,本文将L-DACS1与DME时频域交叠的干扰场景建模为确定性信号叠加高斯有色噪声的干扰量化模型,根据两者在高阶统计域的差异特性,提出基于三阶累积量的自适应滤波算法,并引入对数螺线函数改进变步长机制,实现自适应DME干扰消除.仿真结果表明:所提算法具有更高的干扰抑制比和更低的误比特率,但复杂度较高.相关结论可为L-DACS1系统的实际部署提供参考.

L波段数字航空通信系统;测距机系统;高阶统计量;干扰消除;自适应滤波

1 引言

对以航空短波通信、甚高频模拟通信和甚高频数据链为主的现有航空通信难以满足未来航空通信高速发展需求[1],欧洲航空安全组织和美国联邦航空管理局提出机场场面通信采用C波段机场移动通信系统,陆地空域采用L波段地空数据链,海洋和偏远区域采用卫星通信,各网络之间采用下一代互联网协议进行互联的未来航空通信基础架构[2],并明确指出在已部署航电系统基础上,实现新兴技术和现有航空通信系统多系统共存并逐步演进的技术路线,为航空运行服务和航空通信服务提供更为安全、可靠、实时性高的信息交互,最终完成向未来航空通信的过渡.

L-DACS是未来航空通信地空数据链的候选技术,包括L-DACS1和L-DACS2两种备选方案.相较于L-DACS2,L-DACS1具有更高的频谱利用率、更灵活的频谱扩展性和更强的抗突发脉冲噪声能力而受到广泛的关注.L-DACS1工作频段为960～1164MHz,该频段已部署DME系统、二次雷达系统、空中防撞系统等航电系统.上述航电系统已被分配固定的授权频段,L-DACS1的可用频段表现出明显的离散特性.为提高频谱利用率,L-DACS1以非连续内插方式在相邻1MHz的DME频谱空隙间实现宽带数据传输.如何满足未来航空通信需求并与DME保持兼容是L-DACS1部署首要解决的关键问题.DME信号功率强、频率范围宽、地面覆盖广,是L-DACS1的主要干扰源,其干扰类型属于加性共信道干扰,将引起信号失真,此外多普勒效应、非理想滤波和非线性色散信道还将造成DME信号的频谱泄露,严重影响L-DACS1同步接收性能.因此L-DACS1与DME共存与干扰抑制问题是L-DACS1面临的主要挑战之一.围绕该技术挑战,国内外进行了大量研究:(1)电磁兼容特性分析:文献[3]从空空、空地、地空和同址4类干扰场景出发,对DME和L-DACS1系统分别进行电磁兼容特性测试.结果表明:DME对L-DACS1的干扰影响不可忽略;(2)脉冲消隐/限幅技术:文献[4]最早提出对超过门限值的信号采取消隐或者限幅操作,以实现多载波调制技术的加性干扰抑制.文献[5]沿用文献[4]的研究结果,抑制DME对L-DACS1的干扰,但没有给出性能增益和门限值选取等问题的求解思路.文献[6～8]给出采用脉冲消隐技术时接收端信噪比的闭式解,并得到最优门限值的数学表达式;(3)时频域干扰抑制:文献[9]采用时域加窗的方式实现多载波调制系统的干扰抑制.文献[10]采用频域陷波技术实现DME干扰的抑制.上述各类方法多以DME与L-DACS1在时域、频域或低阶统计域的差异为基础实现干扰抑制.然而DME与L-DACS1在时频域存在严重交叠,上述方法效果并不理想;由时域加窗和脉冲消隐技术带来码间干扰和子载波间干扰还将进一步降低L-DACS1性能[11].因此针对现有基于时域、频域、低阶统计域的干扰抑制技术无法有效解决DME对L-DACS1干扰的问题,本文将根据两者在高阶统计域的差异特性,提出基于高阶统计量的自适应DME干扰消除算法,以解决L-DACS1与DME的兼容性问题.

2 特性分析

高阶统计特性是随机变量或者随机过程三阶及以上的统计特性,其优势在于:(1)抑制加性有色高斯噪声的影响;(2)提取高斯性偏离引起的特征信息;(3)辨识非最小相位系统和非线性系统[12].利用高阶统计量可完全抑制高斯噪声的优势,本文拟寻求一种特征明显、计算量小的高阶统计量实现DME干扰消除.根据矩-累积量转换公式,高阶矩的估计复杂度随阶数的增加而增加,可得三阶累积量计算量最小.因此本文选取三阶累积量作为分析对象,并详细介绍DME与L-DACS1信号三阶累积量的相关性质.

2.1 DME的高阶统计特性分析

DME系统是国际民航组织批准的近程导航系统,如图1所示,DME系统的时域信号由一对高斯脉冲组成,其数学表达式为[5]

(1)

其中,α是决定脉冲宽度的常数,且α=4.5×1011s-2,Δt是脉冲对间隔,Δt=12μs或者36μs.

DME信号是持续时间有限且满足各态历经性的确定性信号,其集总意义和时间意义下的三阶累积量相等,因此三阶累积量可表示为[13]

C3,DME(τ1,τ2) = ∫p(t)p(t+τ1)p(t+τ2)dt

其中,τ1和τ2是相互独立的时间间隔.

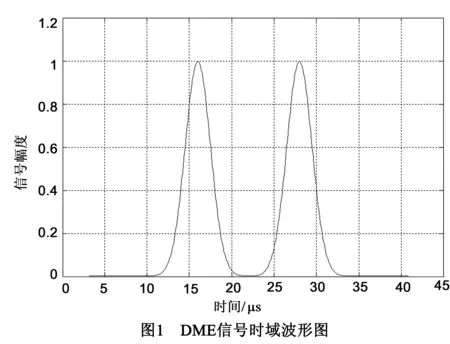
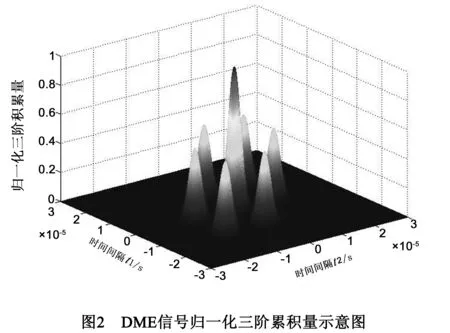
图2所示,DME三阶累积量是关于时间间隔τ1和τ2的圆对称三维曲面,包括中心坐标在(0,0)、(Δt,0)、(Δt,Δt)、(0,Δt)、(-Δt,0)、(-Δt,-Δt)、(0,-Δt)的7个二维高斯函数,且中心坐标在(0,0)的二维高斯函数的峰值是其余高斯函数的两倍.各高斯函数的相关系数ρ=0.5,方差σ2=2/α.DME信号信号脉冲宽度越窄,其三阶累积量域的二维高斯函数越陡峭.当α趋于无穷大时,DME信号将退化为时间间隔为Δt的双脉冲信号,其三阶累积量域的高斯函数由于方差趋于0而退化为冲激函数.

2.2 L-DACS1的高阶统计特性分析

L-DACS1系统采用多载波调制技术,其时域信号表达式为[11]

(3)

其中,dn,k是第n时刻,第k个子载波调制映射的数据符号,满足零均值和相互独立的,K是子载波个数,fc是载波中心频率,Δf是子载波间频率间隔,g(t)是成形脉冲函数,Ts是码元持续时间.在子载波数足够大的情况下,根据中心极限定理,OFDM信号的时域包络具有渐进高斯性,即OFDM信号等效为平稳高斯过程,理论上其三阶及以上累积量恒为0[14].

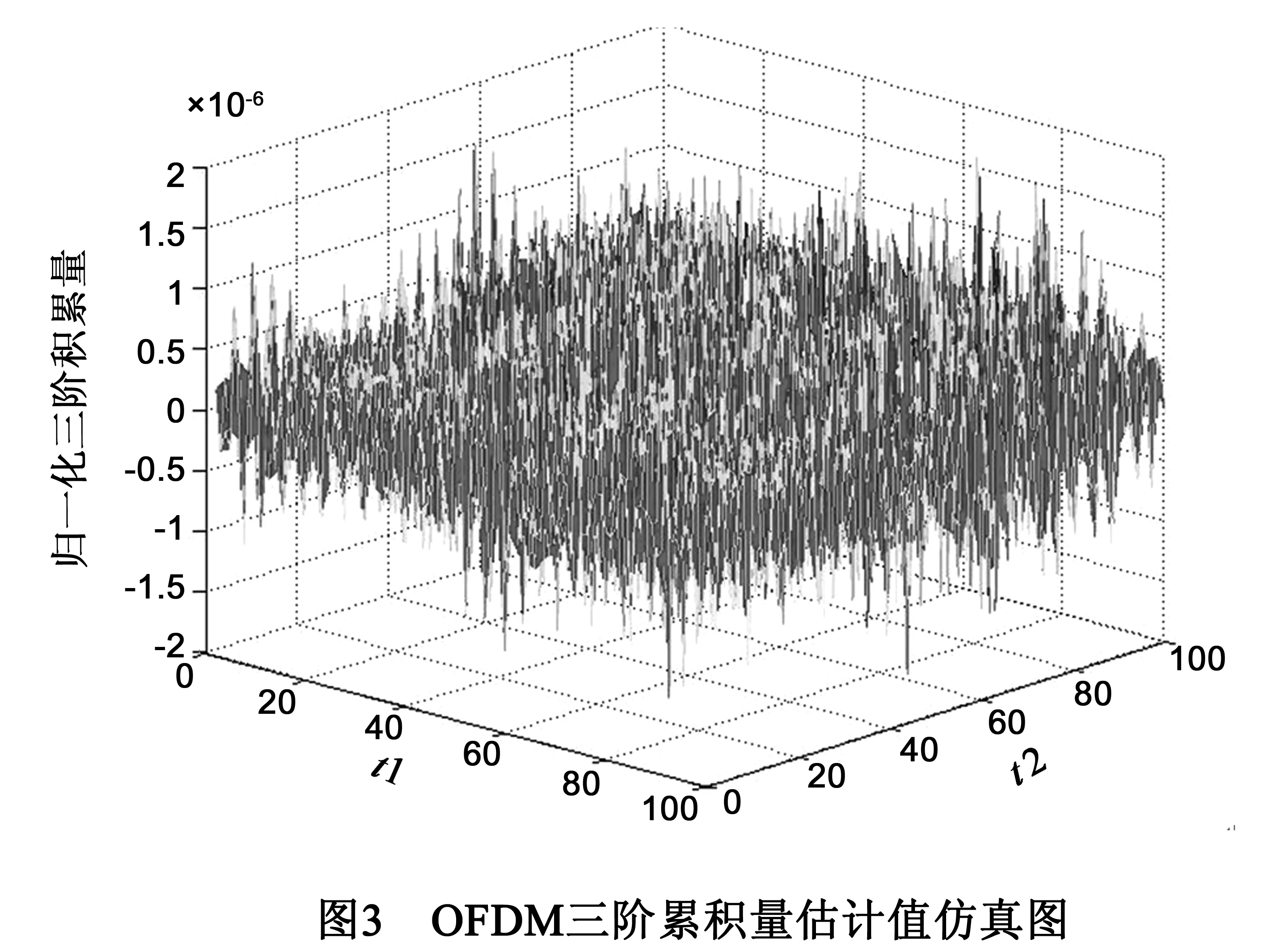
如图3所示,L-DACS1信号三阶累积量的非参数化法估计值均在10-6以内,与平稳高斯随机过程三阶累积量恒为0的结论一致,因此证明L-DACS1信号时域包络服从高斯随机过程的假设成立.

3 算法设计

3.1 CE-LMS的模型建立

第2节分析可知,L-DACS1与DME时频域交叠的干扰场景可建模为确定性信号叠加高斯有色噪声的干扰量化模型.DME为周期、脉冲对间隔等参数确定的高斯脉冲对,其三阶累积量由多个二维高斯函数组成;L-DACS1采用多载波调制技术,其信号时域包络具有渐进高斯特性,可等效为高斯有色噪声,其三阶累积量趋于0.两者相互独立,且在高阶统计域表现出明显的差异特性.干扰消除技术的设计准则是实现L-DACS1与DME特定统计特性的差异最大化.据此本文提出基于高阶统计量的自适应滤波算法CE-LMS (Cumulant Error Least Mean Square)消除DME对L-DACS1的干扰.

图4为CE-LMS算法的流程框图.发射端将已调制数据序列Sk经IFFT变换后产生时域发射信号x(t);假设接收端在理想定时同步和载波同步的情况下,接收信号y(t)受DME信号p(t)和加性高斯噪声n(t)影响,

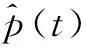
CE-LMS算法的优势是利用高阶统计量抑制高斯有色噪声的特性能够有效处理含高斯有色噪声的观测数据,而基于二阶统计量的自适应滤波算法只能处理含加性高斯白噪声的观测数据,对高斯有色噪声较为敏感.因此,CE-LMS算法能够在不受L-DACS1(高斯有色噪声)影响的情况下精确估计DME信号,并从L-DACS1与DME的混合信号减去DME估计值,实现对DME信号的自适应干扰消除.

3.2 CE-LMS的代价函数

文献[15]提出的基于三阶累积量的MMSE准则是经典的高阶累积量误差准则,其代价函数为

(4)

该代价函数实质上是由双谱Bx(ω1,ω2)的特殊切片(即沿x轴的径向横截面Bx(ω1,0))推导得到的等效均方误差准则,其中双谱是三阶累积量关于ω1和ω2的二维离散傅里叶变换.J3准则的优点是保证均方误差最小的同时,还能够有效抑制高斯噪声.但是由于J3准则只观察三阶统计量的特殊切片,该准则并不能完备地表示L-DACS1与DME的高阶统计特性,即无法完全利用高阶域的先验信息.

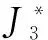
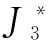
={E[e(n)e(n-τ1)e(n-τ2)]}2

(5)

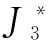
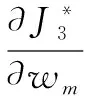
=2e(n)e(n-τ1)e(n-τ2)

·{3W(n)Cpnpn-τ1pn-τ2W(n)T-2W(n)

·(Cpnpn-τ1yn-τ2+Cynpn-τ1pn-τ2+Cpnyn-τ1pn-τ2)

+Cpnyn-τ1yn-τ2+Cynpn-τ1yn-τ2+Cynyn-τ1pn-τ2)

(6)

Cpnpn-τ1pn-τ2=

(7)

Cpnpn-τ1yn-τ2=

(8)

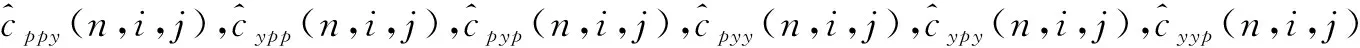
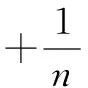
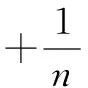
(9)

3.3 CE-LMS的变步长机制

由于自适应滤波算法在收敛速度、跟踪速度以及收敛精度方面对步长调整的要求是相互矛盾的,因此本文参考文献[17]提出的变步长机制思想,建立μ(n)与e(n)之间的非线性函数关系,以提升自适应滤波算法的性能.CE-LMS算法的步长μ(n)是e(n)的对数螺线函数,可表示为

μ(n)=ψ·(exp(β·e(n))-θ)

(10)

其中,ψ,β和θ均为常数.对数螺线的性质保证了算法在初始阶段具有较快的收敛速度,收敛阶段步长逐渐减小避免稳态失调,以提高算法收敛性能.

3.4 CE-LMS算法实现及复杂度分析

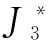
综合考虑算法所有步骤,可得CE-LMS算法的乘法运算量S(n)和时间复杂度T(n)以及基于三阶累积量的MMSE算法的乘法运算量S′(n)和时间复杂度T′(n)分别为

S(n)=(3×M×M+16×M+(U+1)×U/2+6)×n

T(n)=ο(n)

S′(n)=(5×M+4)×n

T′(n)=ο(n)

其中,n为循环次数,M为抽头系数向量维度,U为指数函数的泰勒级数展开的阶数.

CE-LMS算法的累积量迭代更新和梯度计算需要进行繁复的乘法运算,因此CE-LMS算法是以牺牲算法复杂度的代价换取干扰抑制比和误比特率等性能的提升.但是两者的时间复杂度都是线性阶ο(n),因此CE-LMS算法仍具有较高的执行效率.

4 性能仿真

4.1 仿真平台

本文搭建L-DACS1与DME系统共存时的前向链路物理层仿真平台以验证CE-LMS的算法性能.L-DACS1的物理层关键技术为OFDM多载波调制技术,地面最大发射功率46dBm,工作频段为985.5～1008.5MHz,载波带宽为625kHz,子载波数为64,子载波间隔为9.765kHz.L-DACS1的符号长度为120μs,其中包括OFDM信号符号长度为102.4μs和循环前缀长度为17.6μs(保护间隔4.8μs和窗函数长度12.8μs),调制方式是QPSK[11].DME系统的工作频段为962～1024MHz,地面最大发射功率为53dBm,脉冲对间隔为12μs,脉冲对宽度为3.5μs[5].基于此,本文以时域加窗、脉冲消隐、基于三阶累积量的MMSE(Minimum Mean Square Error)算法作为比较对象,通过300次蒙特卡洛实验获得平均指标参数,从干扰抑制比、系统误比特率和误差均方根评估CE-LMS算法的优越性,并验证了CE-LMS算法的误差收敛和跟踪性能.

4.2 性能分析

干扰抑制比定义为干扰抑制前后功率之比,是反映干扰抑制性能的度量单位.由图5可知:(1)信噪比越大,上述算法的干扰抑制比越高,即干扰抑制性能与信干噪比正相关;(2)时域加窗和脉冲消隐的干扰抑制性能一致且均不理想,原因是两者具有在一阶统计域进行干扰抑制的共性,由此引起的码间干扰和子载波间干扰导致干扰抑制比一直维持较低水平;(3)相较于时域加窗(脉冲消隐)和基于三阶累积量的MMSE算法,CE-LMS算法在信噪比0～10dB的情况下分别有2～6dB和0.5～1.5dB的显著提升,干扰抑制能力更强.

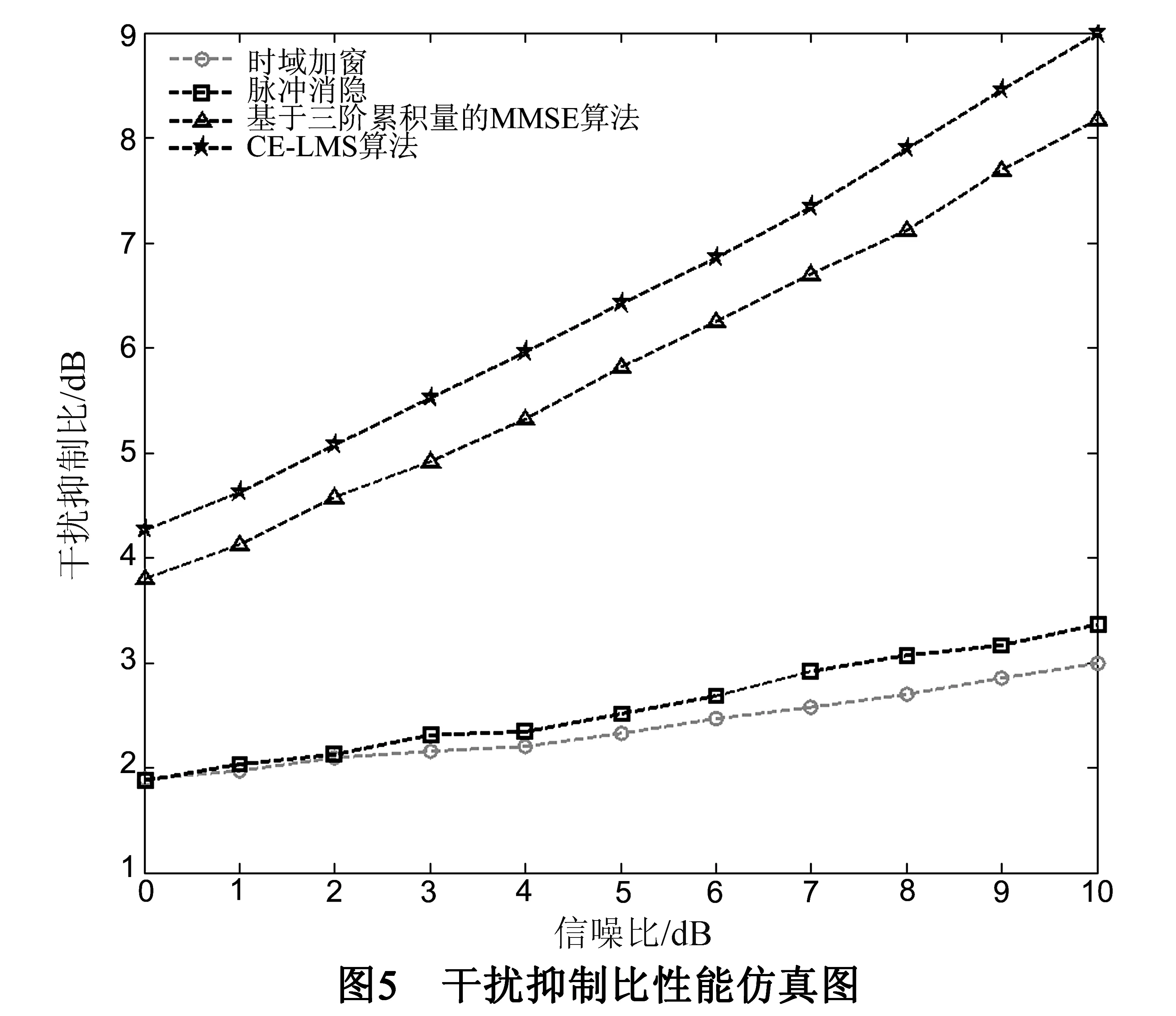
图6为时域加窗、脉冲消隐和基于三阶累积量的MMSE算法以及CE-LMS算法的系统误比特率曲线.由图5可知:(1)相较于时域加窗(脉冲消隐算法)和基于三阶累积量的MMSE算法,CE-LMS算法在信噪比0～10dB情况下分别有0.5～4dB和0～2dB的误差增益;(2)信噪比越大,CE-LMS算法的性能提升越大,且更逼近理想的误比特曲线,表明CE-LMS算法的性能优于传统干扰抑制算法,但性能提升程度受地空通信信道环境影响.

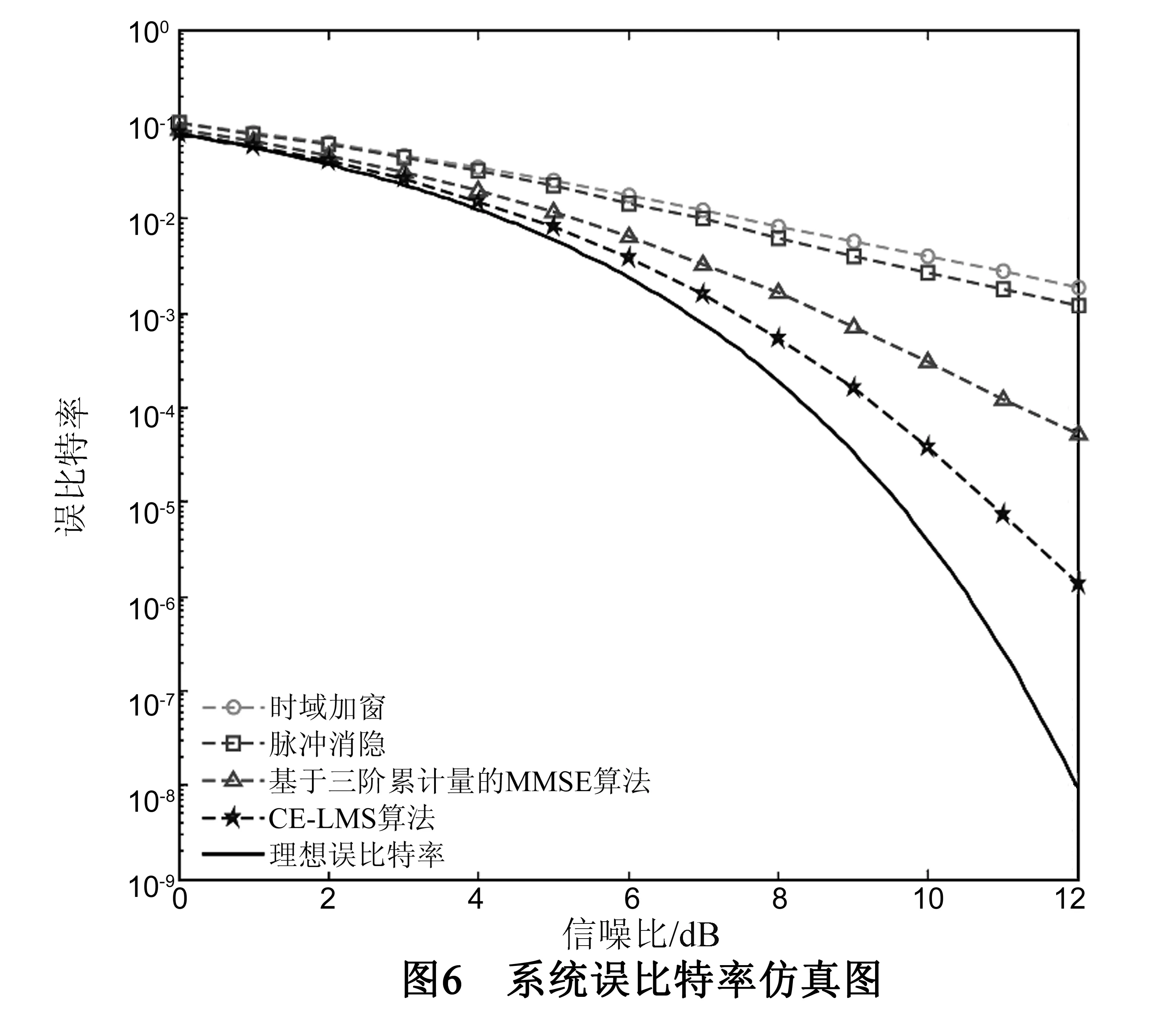
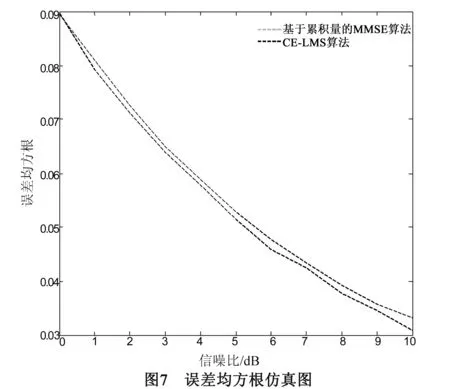
图7为基于三阶累积量的MMSE算法与CE-LMS算法的误差均方根曲线.由图6可知:(1)信噪比越大,自适应算法受到信道高斯白噪声的影响越小,因此算法的误差均方根越小;(2)相较于基于累积量的MMSE算法,CE-LMS算法的误差均方根曲线下降更快,具有更低的稳态误差,误差收敛性能提升范围在0～0.01,表明CE-LMS算法的收敛和跟踪性能更好.

5 结束语

为提高L-DACS1抗DME干扰的能力,本文将DME与L-DACS1时频域交叠的干扰场景建模为确定性信号叠加高斯有色噪声的干扰量化模型,并据此提出CE-LMS算法.该算法采用三阶累积量作为体现两者差异性的高阶统计量,以误差信号三阶自累积量的平方作为代价函数,结合基于对数螺线的变步长机制,以解决L-DACS1与DME的兼容性问题.数值结果表明:与时域加窗、脉冲消隐和基于三阶累积量的MMSE算法相比,CE-LMS算法在复杂度ο(n)增加的前提下,干扰抑制比性能可提升0.5～6dB,误比特率逼近理想误比特率曲线,系统性能有0.5～4dB的改善.相较于基于累积量的MMSE算法,其误差均方根更小,表明CE-LMS算法的收敛和跟踪性能更好.相关结论可为L-DACS1系统与航电系统共存时的抗干扰研究提供解决思路.

[1]Neji N,De Lacerda R,Azoulay A,et al.Survey on the future Aeronautical communication system and its development for continental communications[J].IEEE Transactions on Vehicular Technology,2013,62(1): 182-191.

[2]Schnell M,Epple U,Shutin D,et al.LDACS: future aeronautical communications for air-traffic management[J].IEEE Communications Magazine,2014,52(5): 104-110.

[3]Schneckenburger N,Franzen N,Gligorevic S,et al.L-band compatibility of LDACS1[A].IEEE 30th Digital Avionics Systems Conference[C].USA: IEEE,2011.1-11.

[4]Zhidkov S V.Analysis and comparison of several simple impulsive noise mitigation schemes for OFDM receivers[J].IEEE Transactions on Communications,2008,56(1): 5-9.

[5]Brandes S,Schnell M.Interference mitigation for the future aeronautical communication system in the L-Band[A].7th International Workshop on Multi-Carrier Systems & Solution[C].Germany: IEEE,2009.375-384.

[6]Epple U,Shibli K,Schnell M.Investigation of blanking nonlinearity in OFDM systems[A].IEEE International Conference on Communications [C].Japan: IEEE,2011.1-5.

[7]Zhidkov S V.Performance analysis and optimization of OFDM receiver with blanking nonlinearity in impulsive noise environment[J].IEEE Transactions on Vehicular Technology,2006,55(1): 234-242.

[8]Epple U,Shutin D,Schnell M.Mitigation of impulsive frequency-selective interference in OFDM based systems[J].IEEE Wireless Communications Letters,2012,1(5): 484-487.

[9]Nickel P,Gerstacker W,Jonietz C,et al.Window design for non-orthogonal interference reduction in OFDM receivers[A].IEEE 7th Workshop on Signal Processing Advances in Wireless Communications[C].France: IEEE,2006.1-5.

[10]Coulson A J.Bit error rate performance of OFDM in narrowband interference with excision filtering[J].IEEE Transactions on Wireless Communications,2006,5(9): 2484-2492.

[11]Sajatovic M,Haindl B,Ehammer M,et al.L-DACS1 system definition proposal: deliverable D2[R].Germany: EUROCONTROL,2009.

[12]张贤达.现代信号处理[M].北京：清华大学出版社,2002.

[13]杨福生.随机信号分析[M].北京：清华大学出版社,1990.

[14]Akmouche W.Detection of multicarrier modulations using 4th-order cumulants[A].Military Communications Conference Proceedings[C].USA: IEEE,1999.1:432-436.

[15]Delopoulos A,Giannakis G B.Strongly consistent identification algorithms and noise insensitive MSE criteria[J].IEEE Transactions on Signal Processing,1992,40(8): 1955-1970.

[16]Shin D C,Nikias C L.Adaptive interference canceller for narrowband and wideband interferences using higher order statistics[J].IEEE Transactions on Signal Processing,1994,42(10): 2715-2728.

[17]高鹰,谢胜利.一种变步长 LMS 自适应滤波算法及分析[J].电子学报,2001,29(8): 1094-1097.

Gao ying,Xie sheng-li.A variable step size LMS adaptive filtering algorithm and its analysis[J].Acta Electronica Sinica,2001,29(8): 1094-1097.(in Chinese)

曾孝平 男，1956年生于四川广安，重庆大学教授、博士生导师，重庆大学通信工程学院院长，主要研究方向为空天地一体化、下一代移动通信、生物信号处理等.

E-mail:zxp@cqu.edu.cn

贺 渊 男，1991年生于陕西省洋县，重庆大学硕士研究生，主要研究方向为下一代移动通信、航空移动通信干扰抑制等.

简 鑫(通信作者) 男，1987年生于四川自贡，博士，重庆大学通信工程学院讲师，硕士生导师,主要研究方向为统计数学、无线通信理论与技术、流量分析理论等.

E-mail:jianxin@cqu.edu.cn

Adaptive Interference Cancellation for L-DACS1 by the Usage of High Order Statistics

ZENG Xiao-ping,HE Yuan,JIAN Xin,HUANG Jie,LI Meng-ru

(CollegeofCommunicationEngineering,ChongqingUniversity,Chongqing400030)

To mitigate DME pulse interference over L-DACS1 and overcome the shortage of conventional solutions in time,frequency or second-order statistics domain,an innovative adaptive interference cancellation scheme by the usage of high-order statistics is introduced,namely CE-LMS.CE-LMS models the coexistence of L-DACS1 signal and DME interference as a deterministic signal plus colored Gaussian noises,and employs a cost function based on the three-order cumulant statistics and a variable step adjustment mechanism based on logarithmic function.All this together allow CE-LMS to eliminate the pulse-like DME interference from L-DACS1.Numerical results show that CE-LMS algorithm can achieve a better cancellation ratio and lower bit error rate with a increase in computational complexity,which may help to the deployment of L-DACS1.

L-DACS1(L-band Digital Aeronautical Communication System Type 1);DME(Distance Measuring Equipment);high-order statistic;interference cancellation;adaptive filtering

2015-04-14;

2016-02-01；责任编辑：马兰英

国家自然科学基金重大研究计划(No.91438104);面上项目(No.61571069);青年项目(No.61501065);中央高校基本科研业务费资助项目(No.106112015CDJXY160002);重庆市研究生科研创新项目(No.CYS14005)

TP911.4

A

0372-2112 (2016)10-2377-07

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.10.014