剖析小组合作交流为主线的数学教学活动——以《等腰三角形》一道例题的变式探究课为例

伍春兰 曹建霞

(1. 北京教育学院数学系，北京 100120；2.中国人民大学附属中学朝阳学校，北京 100028)



剖析小组合作交流为主线的数学教学活动
——以《等腰三角形》一道例题的变式探究课为例

伍春兰1曹建霞2

(1. 北京教育学院数学系，北京 100120；2.中国人民大学附属中学朝阳学校，北京 100028)

目前，以小组合作交流的方式开展教学，已经成为了一种时尚，并被广泛地运用到数学课堂教学中．但是在小组合作交流为主线的数学教学活动中，笔者发现仍然存在一些问题，如：交流的问题缺少合作探究的价值；小组合作交流前缺少必要的独立思考的环节；小组合作交流的时间不充分；学生参与度不均衡；教师错失引导时机，点拨不到位等．

下面以人教版《数学(八年级上册)》第十三章13.3《等腰三角形》的一道例题的变式探究课为例，具体剖析.

一、教学活动过程

引例：在△ABC中，AB=AC，D为BC边上中点，点D到AB、AC的距离分别为DE、DF(如图1)，那么DE与DF的关系是什么？请证明你的结论．

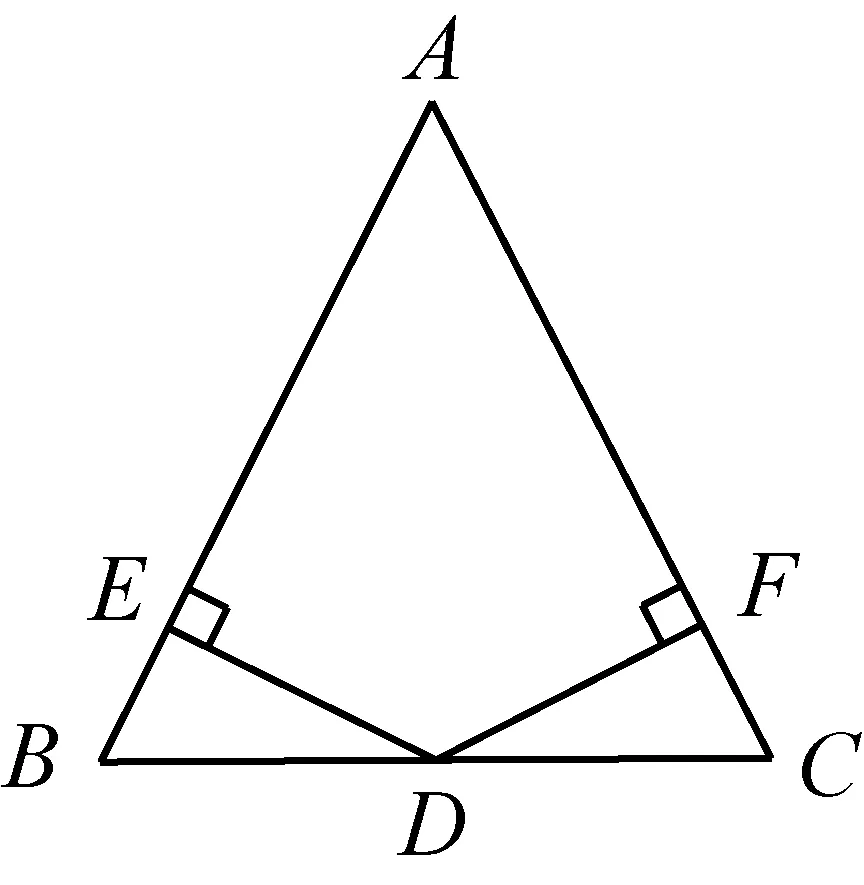
图1

分析：学生四人一组进行探究，很快猜测出DE=DF，并给出了证明DE=DF的方法. 教师请小组代表展示交流不同的思考角度，归纳出三种典型证法. 方法一：利用等腰三角形的性质(三线合一)和角的平分线的性质证明；方法二：利用全等三角形判定及性质证明；方法三：利用面积方法证明．教师肯定了方法三的简洁漂亮，进一步追问学生是怎样想到此方法的，由此让所有学生明白当题目中有高的条件时，可以尝试利用面积来解决问题．

设计意图：观察发现学生都能猜出DE=DF，且至少能用一种方法证明，所以没有必要一开始就要求学生小组交流，而是在学生独立思考有一定想法后再小组或全班交流. 这样不仅让每位学生有机会独立分析和解决问题，同时在不同证法的分析和评议中，丰富他们的解题经验. 而方法三，只有个别学生想到. 但由于在本节课中后面所讲解的题目要用到此方法，因此教师特意做了强调．

变式1：当△ABC不是等腰三角形时，即AB≠AC，D还是BC边上中点，DE与DF的关系又会怎样？

分析：学生先独立思考，然后小组交流．在教师指导下，学生利用面积进行了探讨得出结论：当AB>AC时，DEDF．

设计意图：对于变式1的解决，学生的主要困难有两点：一是想不到分类，二是对用面积方法思考不熟悉．所以在独立思考受阻后，此时小组交流和教师的点拨是学生亟需的．

变式2：“在△ABC中，AB=AC”这个条件不变，我们可以适当改变“D为BC边上中点”这个条件再进行探究，如何改变？

分析：学生在教师的启发下，将点D做了如下更换：(1)D在BC边的中线上；(2)D在BC边的高线上；(3)D在∠A的角平分线上；(4)D为BC边上的一点；(5)D为BC(或CB)延长线上的一点．

之后教师引导学生将点D的变式分为三类：第一类，D在△ABC边上，如情形(4).第二类，D在△ABC内部，如情形(1)、(2)、(3)，且D不在BC边上.第三类，D在△ABC外部，如情形(5)．接下来教师指出：我们就来研究点D为BC边上任意一点，以及D为BC延长线上任意一点的情况.点D到AB、AC的距离分别为DE、DF，那么DE与DF的关系是什么？请四人小组分工，两人研究点D为BC边上任意一点的情形，另两人研究D为BC延长线上任意一点的情形，最后大家交流．

多数小组在探究之初没有思路，教师只好点破：探讨DE±DF与CG(点C到AB的距离)之间的关系．在此提示下，后面的探究较为顺畅，学生证明了下列两个结论．

结论1：△ABC中，AB=AC，D为BC边上任意一点，点D到AB、AC的距离分别为DE、DF，点C到AB的距离为CG(如图2)，则DE+DF=CG．

结论2：在△ABC中，AB=AC，D为BC延长线上任意一点，点D到AB、AC的距离分别为DE、DF，点C到AB的距离为CG(如图3)，则DE-DF=CG.

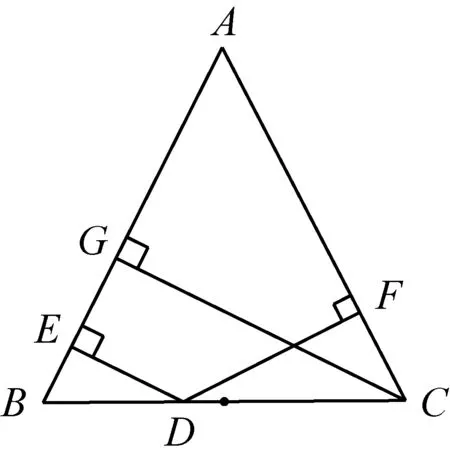
图2

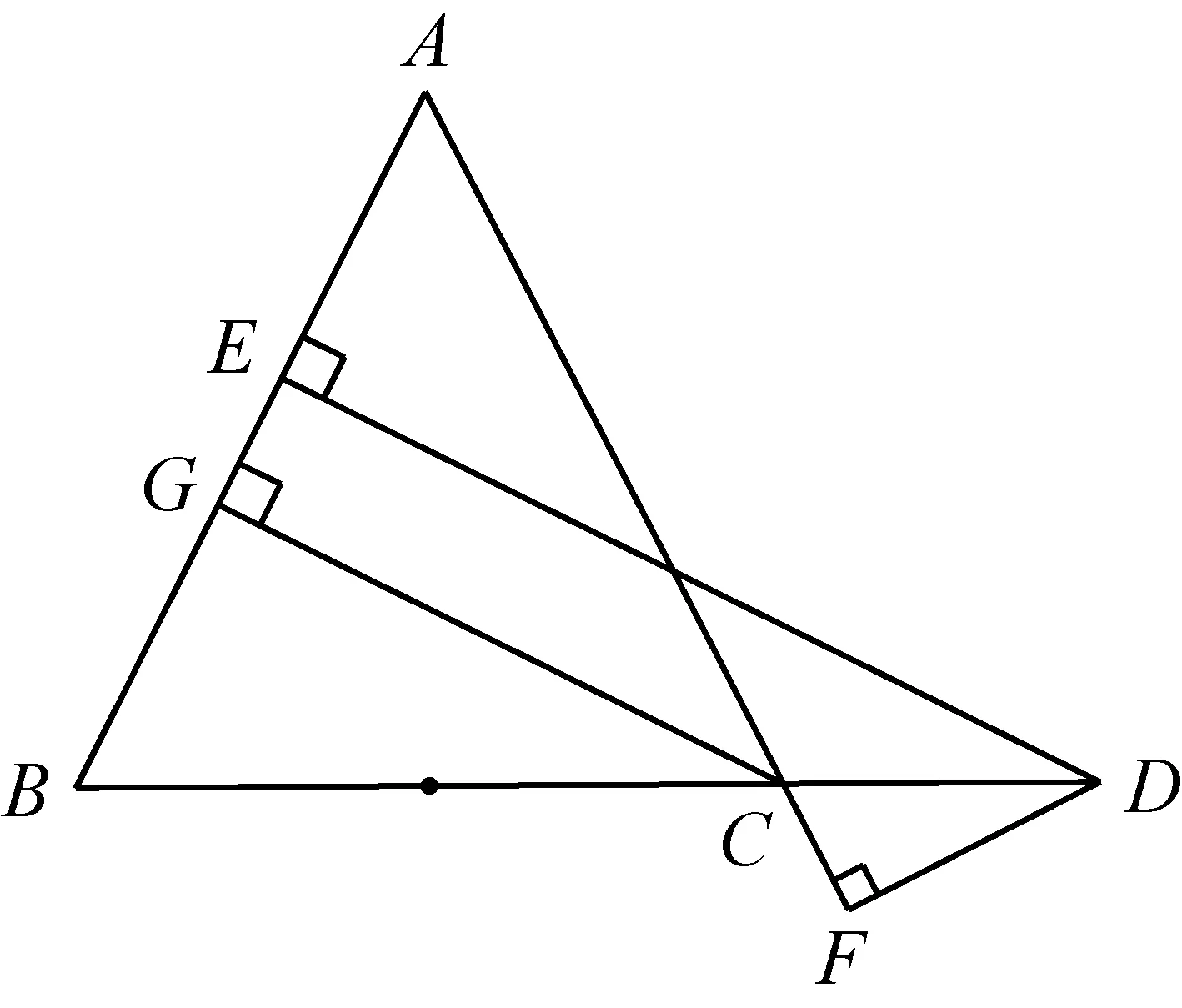
图3

设计意图：教师没有直接给出要解决的两道关于点D的变式题，而是让学生经历题目的变式过程，并通过对点D的分类，展现变式的思考路径.

显然，当D为BC边上任意一点，或D为BC延长线上任意一点时，探究DE与DF的关系是困难的，小组合作是必需的，但当多数小组没有思路时，教师还是要适当引导，让学生探讨DE±DF与CG的关系，因为这是突破难点的关键．

由于时间的原因，最后探究的两道问题又在小组进行了分工，此策略既完整地实现了本节课的目标，又体现了合作交流的优势.

二、教学活动反思

教师找到引例和变式2的共性，将这两道题开放，与变式1构成一个系列探究题，这种改编反映了教师良好的学科水平，也为学生提供了探究学习的发散空间，值得提倡．与此同时还察明学生的最近发展区，适度搭建沟通两道题的桥梁．事实上，两条线段除了相等和不等关系外，还可以启发学生考虑做运算后的某些不变的性质．比如，让学生探讨DE+DF是否为定值，如果是定值，这个定值可以是三角形哪条线段的数值. 进一步启发学生通过特殊点(如D为BC边上的中点)先行研究，然后将结论推测到一般情况(D为BC边上的一点)并证明. 这样的探究，不仅突破了变式2的难点：将DE、DF的关系转换成它们的代数和与CG的关系，也让学生经历了发现问题、提出问题、分析问题和解决问题的全过程．

通过一个题目的系列变式，让学生感受到用面积证明的巧妙之处，这个意图是好的，但不必限制对引例的变式．在变式1呈现前，先让学生充分对引例多角度地变式：结论和条件的互换，改变一个条件或结论，题目呈现的改变等．比如，把引例DE=DF作为条件，寻求点D的位置．即可表述为：当点D在什么位置时，DE=DF？还可表述为：添加一个条件，使DE=DF．再如，引例的条件：AB=AC，D为BC边上中点不变，把DE、DF分别变为AB、AC上的中线或∠ADB，∠ADC的平分线，DE和DF是否相等.当然还可以利用等腰三角形的轴对称图形的性质，猜想DE、DF分别变为AB、AC上的n等分线或∠ADB，∠ADC的n等分线的情况．

总之，将变式作为教学资源，让学生参与其中，了解变式题的前世今生，然后再根据本节课所定的目标，选择变式题加以实现．这种发散思维与集中思维并举的学习方式，有助于学生学习能力的提升和创新意识的培养．

三、教学活动建议

以学生小组合作交流为主线的教学活动，除了通过信息沟通、观点共享、意义生成等思维碰撞，促进学生的数学认知更为丰富、深刻、全面以外，其意义还在于学生主体的充分发挥、多方面心理需求的满足、分析问题与解决问题能力的提高，以及合作交流、团结协作、竞争意识的培养等．因此要取得上述成效，开展以小组合作交流为主线的教学活动时，下面三个问题值得关注．

1. 建立适宜的合作小组

根据活动内容，采用灵活的编组原则，既可以是优中差的组内异质组合，也可以是全优、全中、全差的组内同质组合，还可以是全男、全女的性别组合等．每组人数以4至6人为宜，如人数太少，不利于学生间的讨论、交流和互助；如人数太多，不便管理，也不利于学生间的交流和个人的充分展示，互动得不到体现．每个小组成员在组内承担一个相应的角色，包括组长、记录员、报告员、检查员等．这些角色还可以适当调换，充分调动学生的积极性，确保他们都主动地参与小组活动．

2. 培养基本的合作技能

教师要强化学生团队观念和互帮互学的合作意识，不失时机地向学生传授合作的基本技能，比如倾听、表达、质疑、接纳、组织管理等技能，使他们学会既善于积极主动地表达自己的见解，敢于说出不同的看法；又善于倾听别人的意见，相互启迪，并能够综合吸收各种不同的观点，共同寻找解决问题的思路．

3. 恰当选择合作交流的内容

研究表明，并不是所有的内容都适合小组合作交流．在数学课堂，像学生无法独立在短时间内完成的任务；对学生个人较难完成，但又在学生能力范围内富有挑战性的问题；抑或是开放性或解决途径多样化的问题等，都适合开展小组合作交流活动．

[1]人民教育出版社课程教材研究所，中学数学课程教材研发中心. 义务教育教科书·数学(八年级上册)[M]. 北京: 人民教育出版社，2013：89.

(责任编辑：李 珺)