地震动摇摆分量的合成

姚振亚， 金国芳

(同济大学 土木工程学院， 上海 200092)



地震动摇摆分量的合成

姚振亚， 金国芳

(同济大学 土木工程学院， 上海 200092)

基于入射体波(P和SV波)的波长和傅里叶幅值谱及干涉产生的面波(Rayleigh波)对地震动摇摆分量的影响，给出地震动摇摆分量合成公式.基于弹性波动理论和快速δ-矩阵算法求出设定地壳模型的面波频散曲线，同时考虑了入射体波和面波产生的摇摆分量，并基于Trifunac的研究给出地震动摇摆分量的合成过程.即由设定未来地震的地震震级M、震中距R和场地类别s等条件，利用修正的Trifunac合成公式以合成地震动平动分量，然后考虑体波和面波不同频率成分分量的贡献，合成地表一点处的地震动摇摆分量，并给出三联反应谱.

地震动摇摆分量； 弹性波动理论； 目标傅里叶幅值谱； 入射体波和面波； 三联反应谱

在地震发生时，通常可由安置在地表附近的地震仪记录到地震动的3个正交分量(即包含2个水平分量和1个竖向分量)；然而，地震动应包括3个平动分量和3个转动分量.大量震害现象已经表明，地震动转动分量是引起建筑物破坏的重要原因，建筑物抗扭设计已经为结构工程师所关注.Li等[1]和Awad等[2]的研究表明，即使是对称的建筑物，地震动转动分量仍将引起建筑物的扭转破坏.Hart等[3]的研究已证明对于较大尺度结构(如桥梁，管道或高层建筑等)，地震动转动分量是引起结构破坏的重要原因.Graizer[4]和Bouchon等[5]研究了在均匀介质内的地震断层(包括走滑和倾滑断层模型)附近的地震动转动分量，发现相对于平动分量的幅值而言，转动分量的值是非常小的，但不应被忽略.目前，强震观测仪器仍很难捕获到可供实际工程抗震分析应用的地震动摇摆分量实测记录，因此，通过理论研究从地震动平动分量来获取摇摆分量变得尤为重要.

国内外学者对地震动平动分量和摇摆分量之间的关系进行了很多研究.Lee等[6]推导出在成层的半无限弹性空间中，入射P波、SV波和Rayleigh波所引起的地表处的地震动摇摆分量及应力和位移之间的理论关系.Che等[7]基于1999年台湾集集地震的记录，运用弹性波动理论求得了地震动转动分量，并计算和分析了地震动转动分量的频谱特征.孙士军等[8]，何超等[9]基于频域法利用等效群速度曲线及估算体波入射角求出视波速曲线，从而由实际地震动平动分量求解出转动分量.魏文晖等[10]基于小波变换及阈值处理的原理，由未修正的地震动平动分量求得转动分量，并利用振动台试验加以验证.Graizer等[11]基于地表倾斜造成单摆式地震仪水平和竖向摆的响应差异性，根据地震动平动分量通过傅里叶分析求得转动分量.

随着强震观测仪器的发展，已记录到大量强震发生时的地震动平动分量，这为预测地震动摇摆分量提供了现实基础.然而未来地震的发生及地震震级和震源特性等是未知的，故利用现有地震记录求取地震动摇摆分量并不能完全满足实际工程需要.因此，若可根据任意设定的未来发生的地震特性来合成地震动平动分量，并以此为基础合成地震动摇摆分量，将更便于工程应用.并且，地震波在层状介质中传播有频散特性，目前合成地震动摇摆分量的主要方法(行波法和频域法)都不能体现出地震波的频散效应和相位变化.本文采用Buchen等[12]给出的快速δ-矩阵算法计算出面波频散效应，并根据地震震级、震中距和场地类别，基于Wong等[13]的方法来合成地震动平动分量，在此基础上根据弹性波动理论推导出的地震动平动分量与摇摆分量之间的关系，合成设定条件下的地震动摇摆分量.

文中采用的小波函数形式通过引入群速度Unm和特性因子Q，使合成的地震波可反映由于成层介质引起的面波频散效应和地壳介质材料特性引起的地震波波幅的衰减和相位移动.本文仅对地震动摇摆分量的合成进行了探讨，推演出地震动平动分量和摇摆分量的合成公式及合成过程，并以地震震级M=6.5为示例，求得合成的地震动摇摆分量及相应的三联反应谱.

1 摇摆分量公式推演

理论上可以选择适当的笛卡尔坐标系(x1，O，x2)，使波的传播方向n位于该平面内，则波不依赖于x3坐标[13].对于P波来说，位移矢量垂直于平面波振面，因此波的传播方向在(x1，O，x2)平面内；对于S波来说，位移矢量位于波振面内，且S波的位移矢量可以分解为两个分量：位于(x1，O，x2)平面内的SV波和垂直于该平面的SH波.

当P波、SV波和Rayleigh波入射到均质、各向同性的半无限弹性空间的自由边界面处(x2≤0)时会发生反射，如图1～3所示.由上可知，若选择恰当的平面坐标系(x1，O，x2)，可使入射波和反射波位于该平面内.为便于计算，本文将基于此坐标系建立三维笛卡尔坐标系(x1，x2，x3).

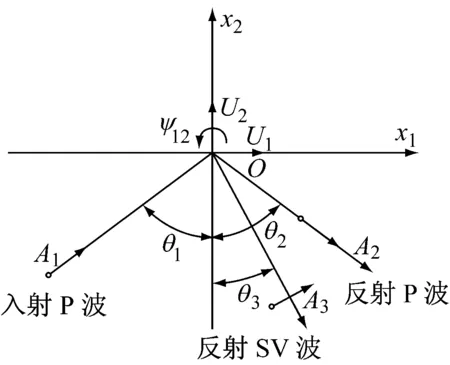
图1 坐标系中由入射P波所引起的摇摆分量ψ12

Fig.1 Coordinate system for rock-ing components caused by incident P-wave

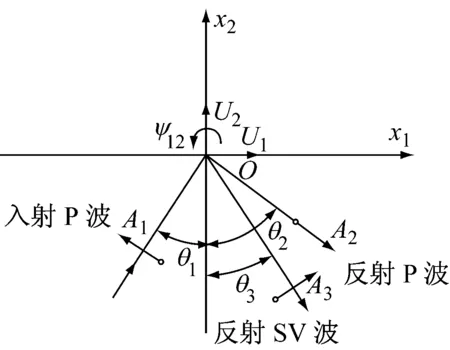
图2 坐标系中由入射SV波所引起的摇摆分量ψ12

Fig.2 Coordinate system for rock-ing components caused by incident SV-wave

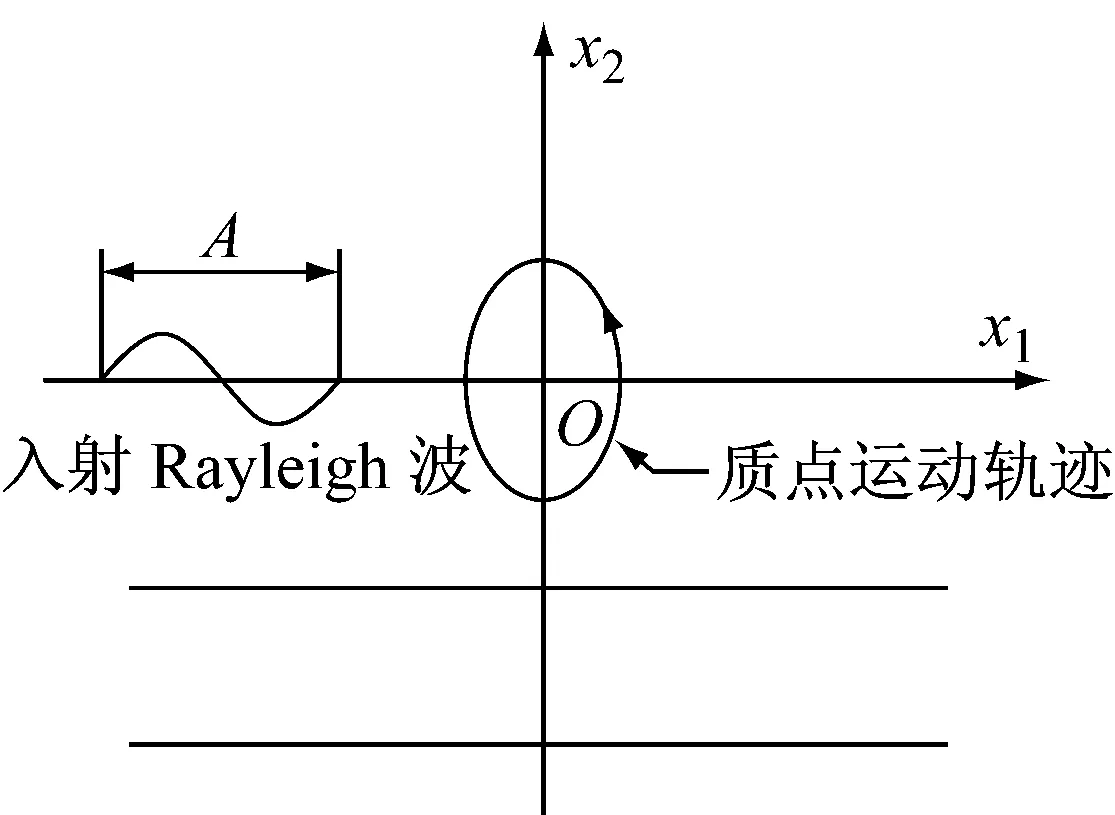
图3 坐标系中由Rayleigh波所引起的摇摆分量ψ12

Fig.3 Coordinate system for rock-ing components caused by Rayleigh wave

1.1 小波包变换

为统一计算，约定傅里叶变换形式如下：

(1)

小波包的设定为将地震动频段(0～25 Hz)划分为非重叠的N个窄频带，并给出每个窄频带上量纲一化处理后的设定目标傅里叶幅值谱，面波可表示为在每个窄频带中心频率处特征函数的叠加，从而叠加求取地震动加速度时程.并记：ωn和Δωn分别为第n个窄频带上的中心频率和半带宽；Unm=Um(ωn)和Cnm=Cm(ωn)分别为第n个窄频带的第m阶模态的群速度和相速度；函数wnm(x;t)为在t时刻，在自由表面处(x2=0)的某点x1处的第m阶模态、第n个窄频带上的加速度时程[14]：

(2)

(3)

(4)

式中：knm为水平复波数；Q为特性因子，若假定材料特性无衰减(即1/2Q=0)，可认为knm为实数[15]；函数wnm(x;t)采用频率ωn的指数形式，并用sinc(·)函数对振动幅值进行调幅，以表示小波包的传播模式.

对小波函数wnm(x;t)进行傅里叶变换得

(5)

1.2 多维地震动平动分量

由于计算主要在频域中进行，首先对时域内的合成公式进行傅里叶变换，经过相关计算后再进行傅里叶逆变换(文中约定采用式(1)的变换形式)，最终得到时域内的地震动平动分量的加速度、速度和位移时程.

基于前述坐标系建立笛卡尔坐标系(x1，x2，x3)，设定x1轴与地震震源到工程场地之间连线平行，由此给出相应的x2轴(横向)和x3轴(竖向)；亦可根据坐标轴旋转公式对其他形式坐标系进行转轴变换.首先给出了频域内地震动平动分量沿径向(x1轴)的加速度、速度和位移合成公式，见式(6)～(8)；类似可得地震动平动分量横向和竖向的相应公式.由前述分析可知，地震动加速度时程ü(x1;t)可通过非重叠的N个窄频带上的一系列小波包的叠加而得到.另外，由于计算主要在频域内进行，可对加速度、速度和位移时程进行傅里叶变换，下面给出了地震动平动分量的加速度、速度和位移在频域内的合成公式：

(6)

(7)

(8)

1.3 地震动摇摆分量

本文设定地震震源为等效点源模型，且地震波从震源到工程场地的地表面附近处所经过的路径分别为基岩和覆盖层.由于地震波从震源到场地的传播过程中，体波将在地壳分层界面处发生多次反射及干涉，进而产生面波，面波在水平层状介质中会由于介质的不均匀性发生频散.当地震波到达地表面附近时，地震波应包括体波(P波和S波)和面波(Rayleigh波)成分，若想获得某一点地表面附近处地震动摇摆分量，应根据不同波型的不同窄带频带波的相速度，分别考虑体波和面波各频率成分的到时t及其在同一时刻内对地表某处地震动摇摆分量的贡献，进而合成地震动摇摆分量的加速度、速度和位移时程.

在均质、各向同性的半无限弹性空间的自由边界面处的摇摆分量ψ12(绕水平轴转动的角加速度)是由P,SV和Rayleigh波在界面处多次反射及干涉而生成.在自由边界处(x2=0)，地震动摇摆分量可由合成的地震动平动分量求得，则某点非零的摇摆分量ψ12可由下式求得：

(9)

式中：j表示x2方向上的单位矢量.

将式(6)～(8)代入到式(9)中，通过化简即可得到地震动摇摆分量的加速度、速度和位移在频域内的合成公式，再对其进行逆傅里叶变换，可得地震动摇摆分量的加速度、速度和位移在时域内的合成公式.

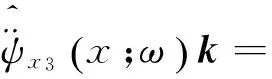
(10)

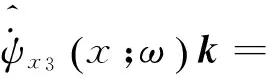
(11)

(12)

式中：k表示x3方向上的单位矢量.

2 摇摆分量的合成过程

根据设定未来地震的地震震级M、震中距R和场地条件s，选择强震振幅和持时等特性的经验标度模型，再由经验标度模型求出给定地震的目标傅里叶幅值谱；地震波从震源到工程场地的传播过程中的频散函数采用快速δ-矩阵算法计算得出，若想获得地表附近某点的地震动摇摆分量，应根据不同波型的不同窄带频带波的相速度，分别考虑体波和面波各频率成分的到时t及其在同一时刻内对地表某处地震动摇摆分量的贡献.利用式(10)～(12)合成在频域内的地震动摇摆分量的加速度、速度和位移，然后对其进行傅里叶逆变换，从而合成最终的地震动摇摆分量ψ12的加速度、速度和位移时程曲线.

2.1 面波的模态参与系数

(13)

(14)

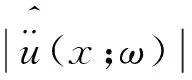
文中假定随机相位角φnm是相对于初始点为震中的扩散系数，并考虑材料衰减因子Q将引起地表不同点处的质点运动的不同.假定地震发生后，震源处(参照点r=0)产生的地震波最初是在基岩中传播，设定r为断裂带边缘至覆盖层的水平距离(此处不考虑震源深度)；当地震波传播到地表附近时，将在覆盖层中传播，设定x为覆盖层的水平长度；设定未来地震的目标傅里叶幅值谱将取决于场地至震中的震源距R和场地类别条件.

2.2 面波频散特性

在水平成层各向同性的半无限弹性空间中存在着多种形式的波，且不同波型在空间不同点处所占的能量是不同的.因此，若合成地表附近某点的地震动，应求出面波的频散曲线.对于面波在层状介质半空间中的传播模式，由于成层地基的面波(Rayleigh波和Love波)的相速度和群速度均随频率f而变化，即具有频散性，且不同场地频散曲线相差很大.本文将采用Buchen等[12]给出的快速δ-矩阵算法计算面波频散曲线，面波的群速度形式Um(ωn)=dω/dkm(ω)，式中km(ω)=ω/Cm(ωn)是水平方向的波数.同时认为，体波在地壳传播过程中无频散效应，即U(ωn)=C(ωn).

2.3 目标幅值谱概述

对于设定未来地震的目标傅里叶幅值谱可由经验标度模型确定，该目标幅值谱可通过设定的未来地震的地震震级、震源深度、震中距、场地类别和超越概率p等进行选择[16].本文场地类别采用场地地质条件参数s来描述(s的取值分别表示：0—淤泥质土，1—中等场地和2—基岩)[17].衰减关系主要是针对强震记录样本的统计结果，不同结果之间往往具有很大的离散性.因此，应尽可能采用根据本地强震记录得出的回归公式，或根据本地区烈度衰减关系近似推导的衰减关系.

3 数值算例

本文选取的地壳构造模型为6层速度模型，层参数见表1.

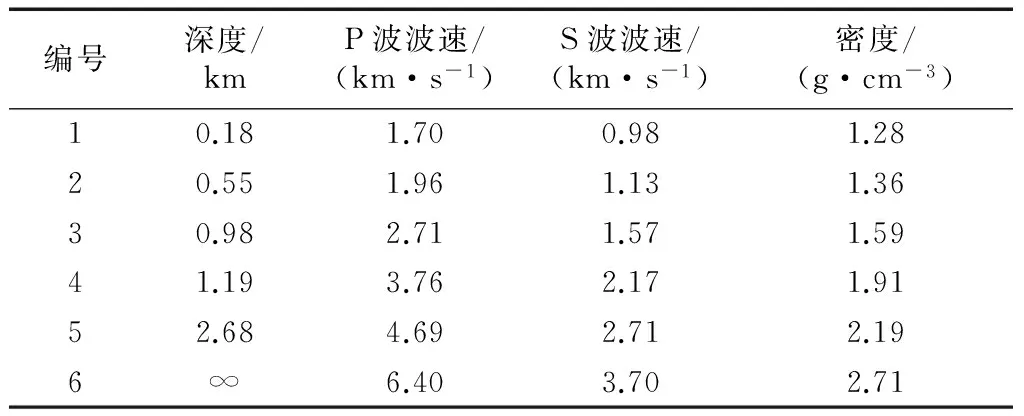
表1 Westmoreland地区地壳模型的层参数

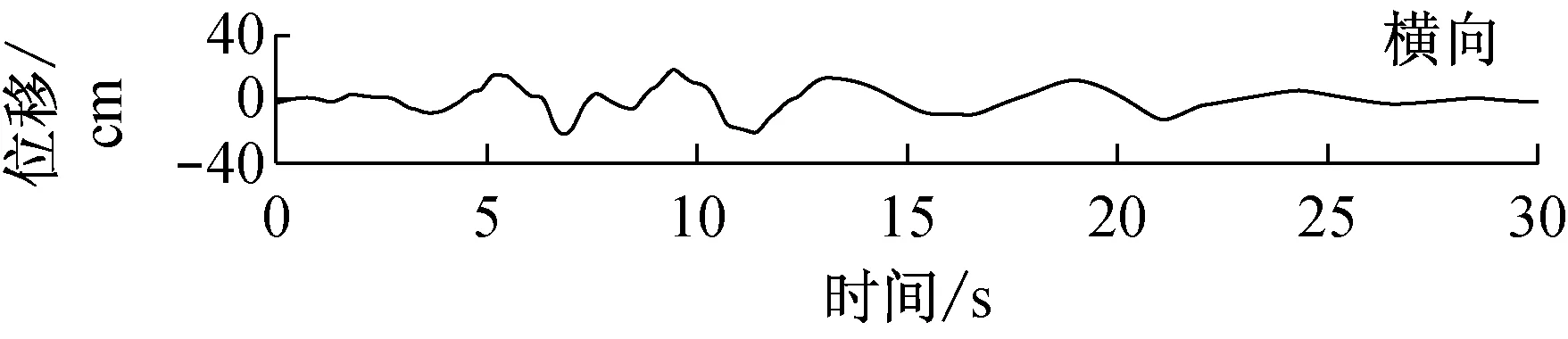
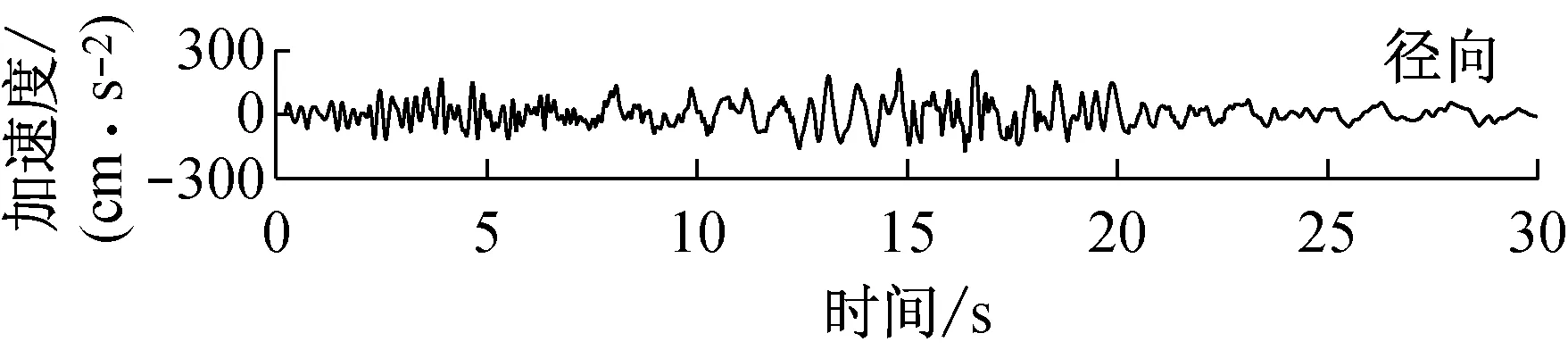
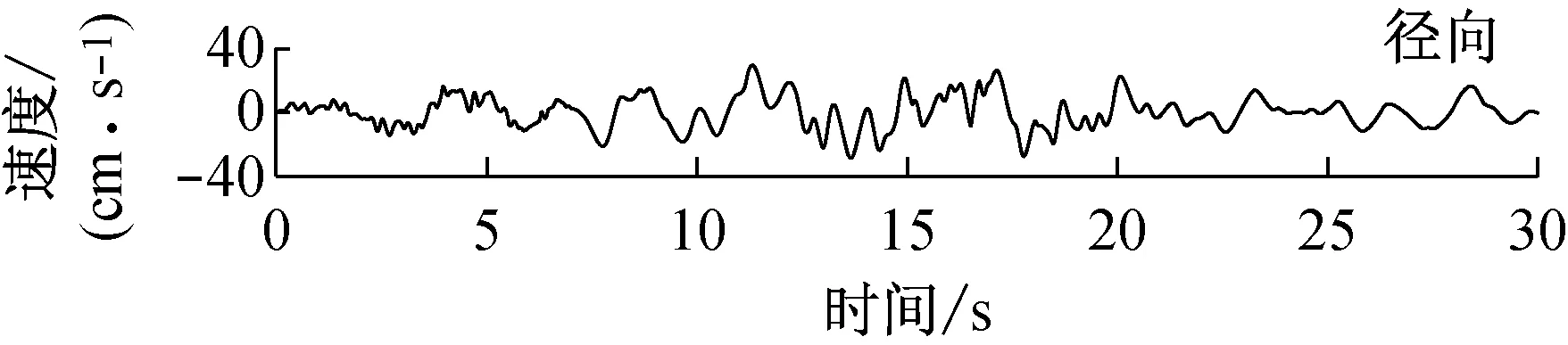
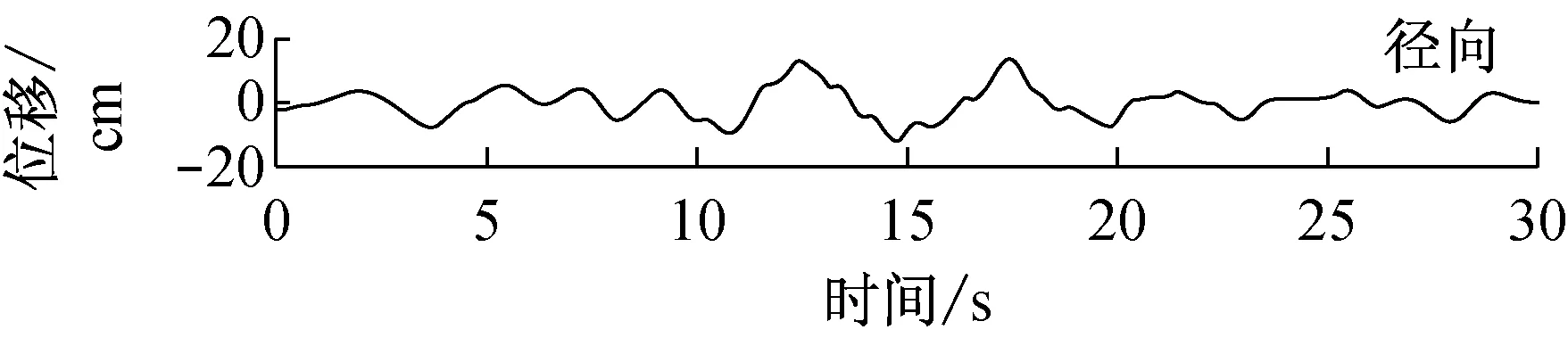
由快速δ-矩阵算法求出Rayleigh和Love波前5阶模态的相速度Cm(ω)和群速度Um(ω)(m=1～5).另外，通常可将体波(P，SV和SH波)作为面波的高频模态处理(其中，P波作为Rayleigh波的第6阶模态；S波作为Love波的第6阶模态).Rayleigh和Love波在f-k域相速度和群速度的的频散曲线分别如图4和5所示.合成的多维地震动平动分量时程(每条地震动时程曲线有4 096个点，时间间隔为0.02 s)如图6所示；再由上节给出的计算方法求出地震动摇摆分量，摇摆分量时程(包括摇摆分量的加速度、速度和位移时程)如图7所示，摇摆分量及三联反应谱如图8所示.图8中，PSA为绝对加速度反应谱，PSV为相对速度反应谱，SD为相对位移反应谱；曲线由上至下依次对应阻尼比为0,0.02,0.05,0.10,0.20.

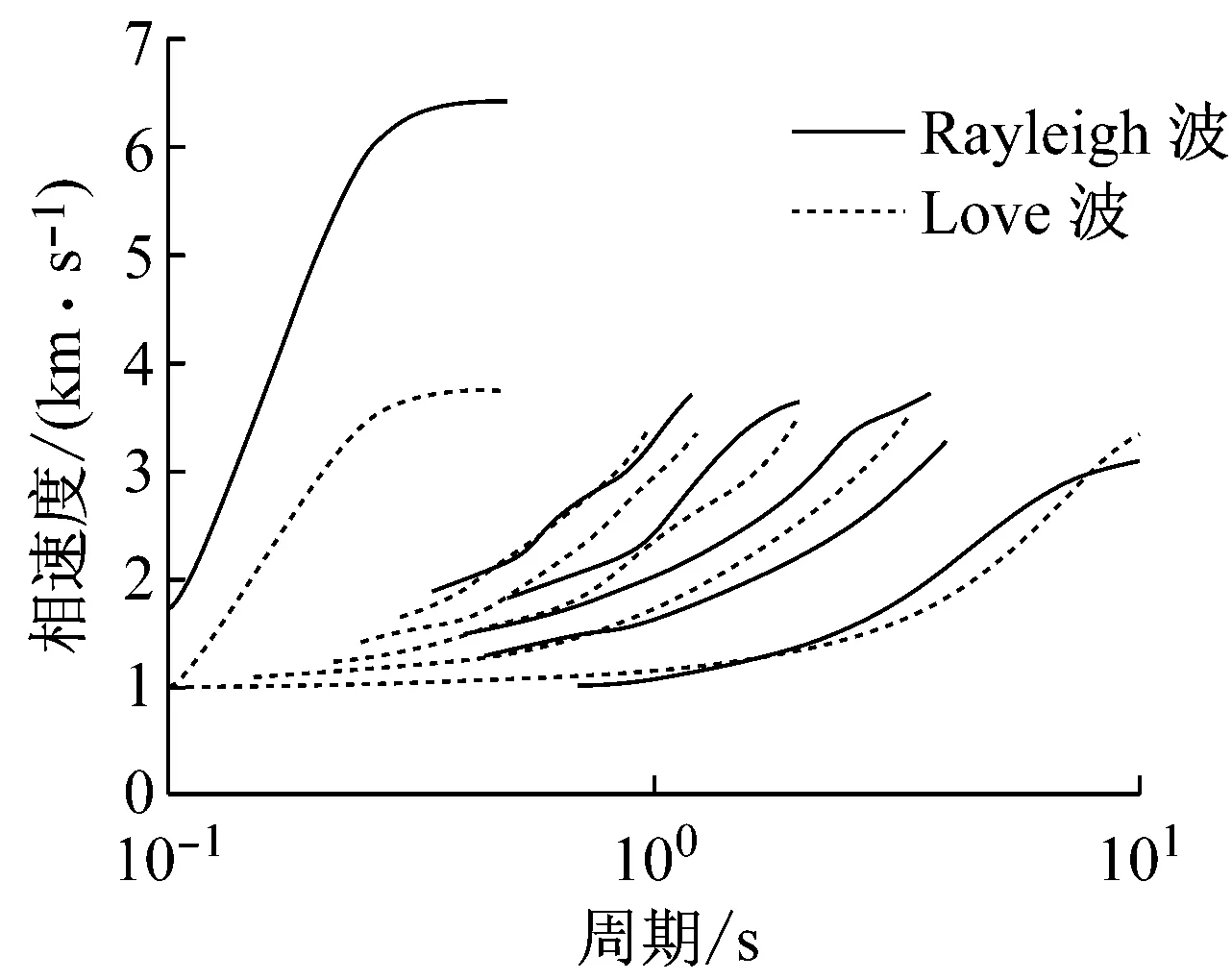
图4 Rayleigh和Love波在f-k域相速度的频散曲线

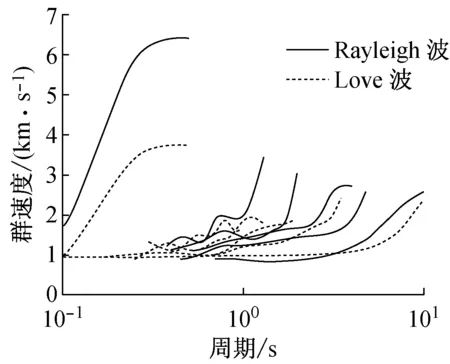
图5 Rayleigh和Love波在f-k域群速度的频散曲线

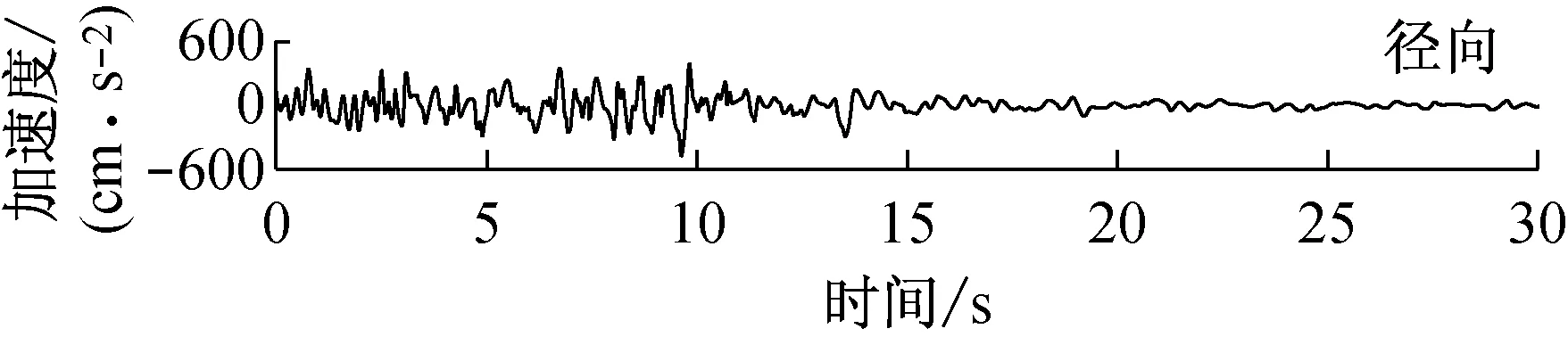
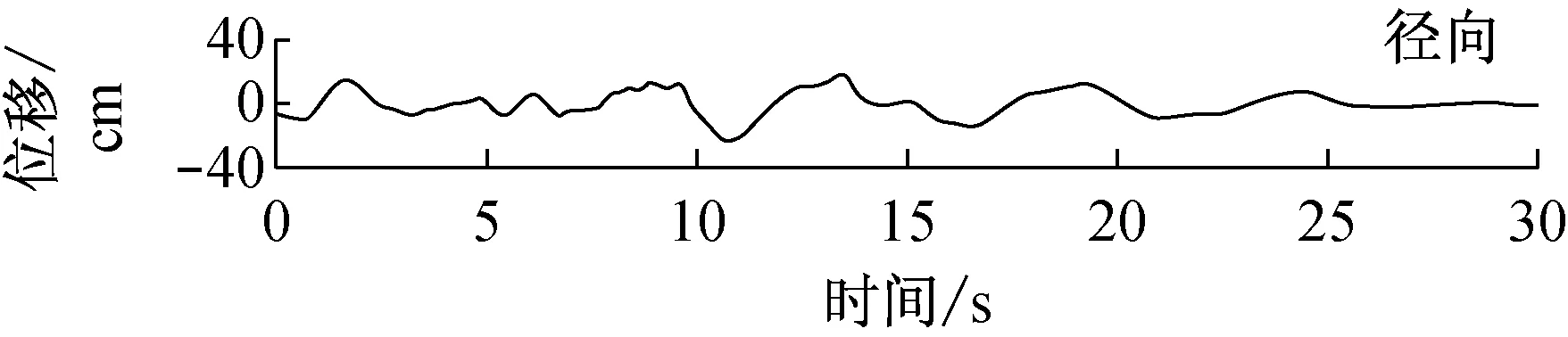
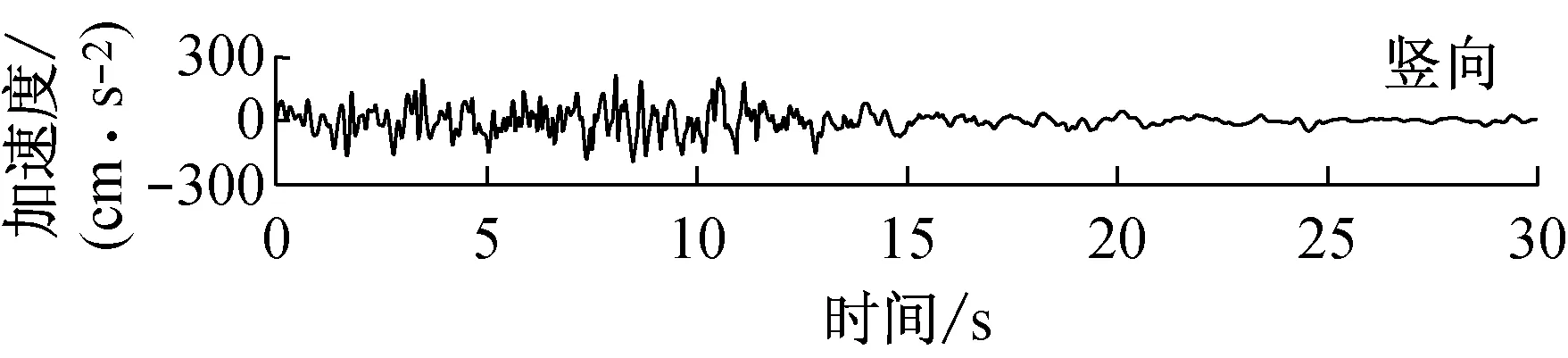
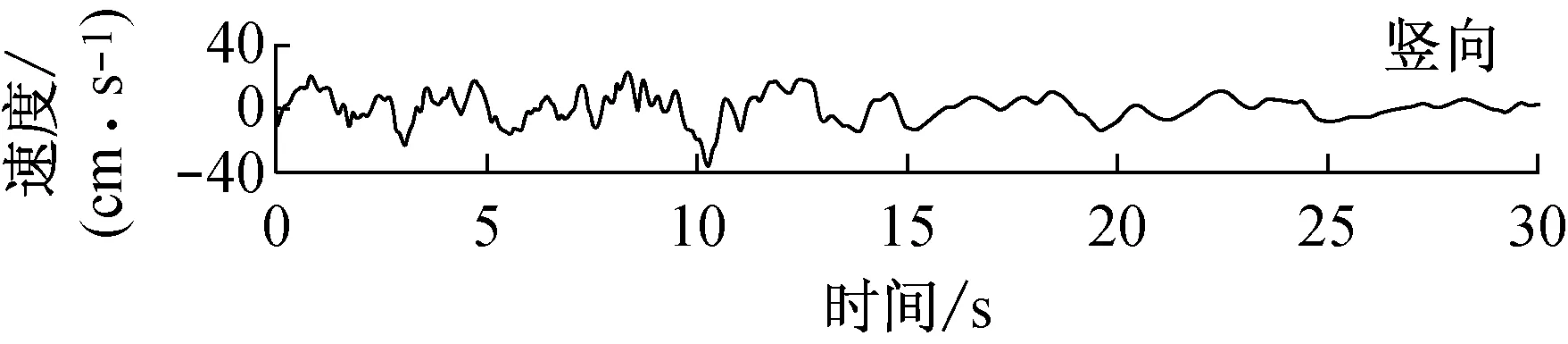
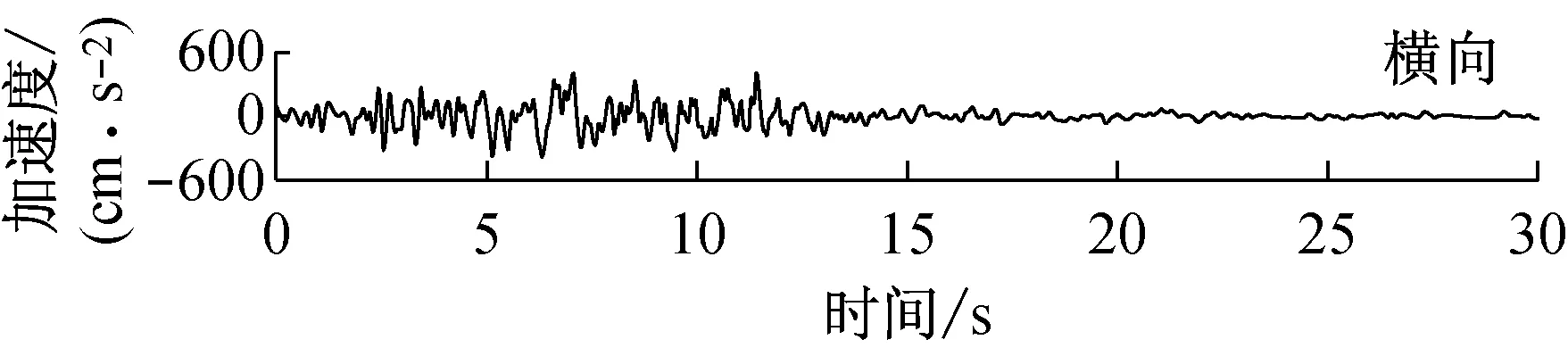
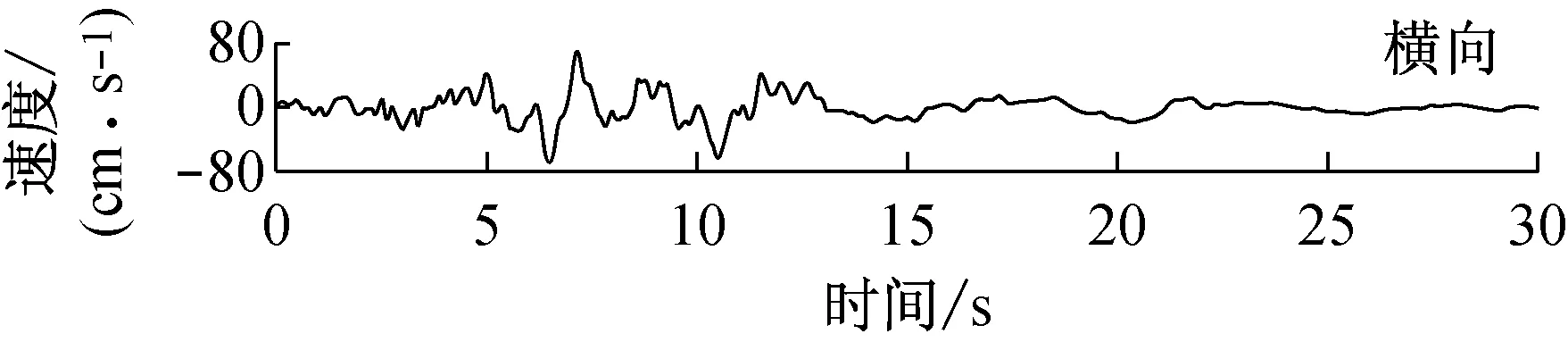
a 目标傅里叶幅值谱:M=6.5,R=10 km,p=0.5,s=0;x=4 km; 频带: 0.125～25 Hz

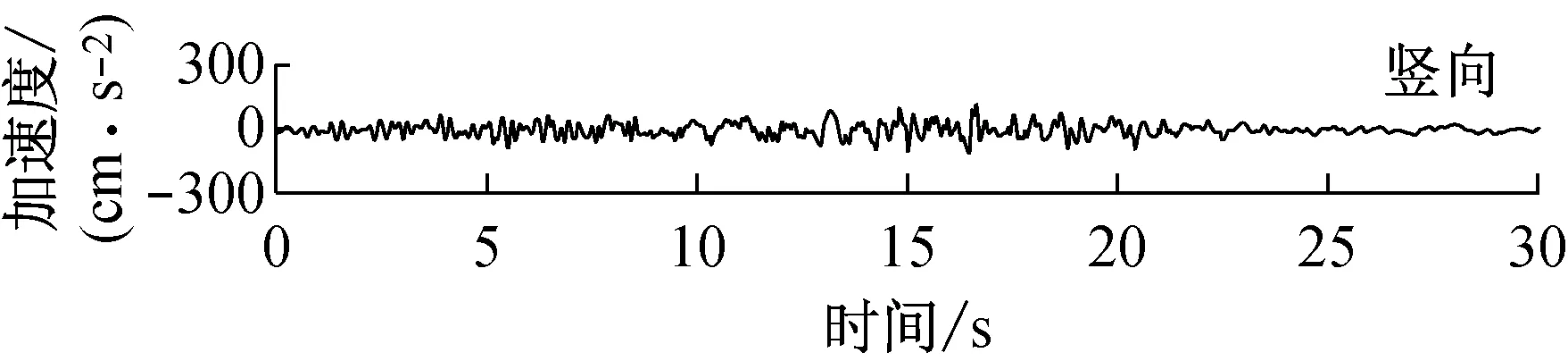
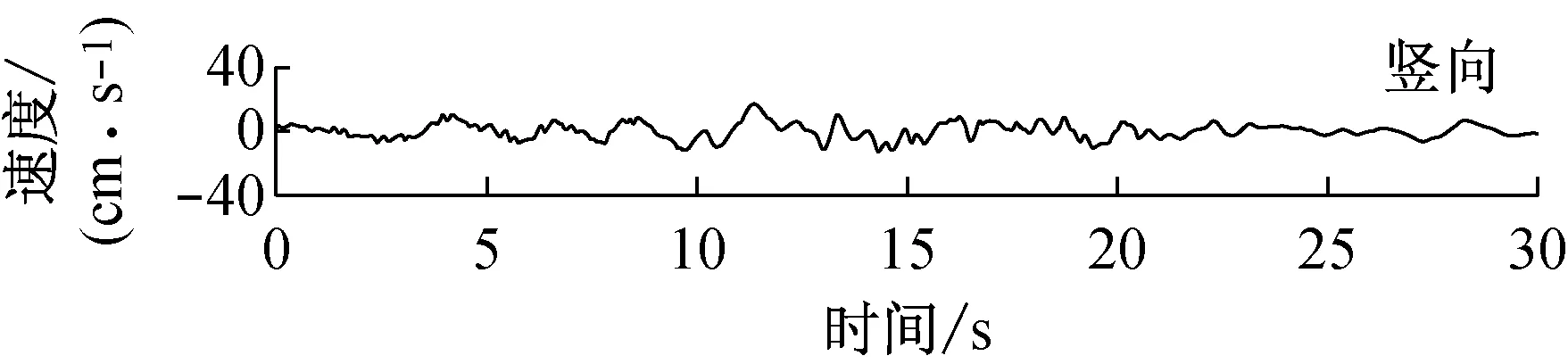
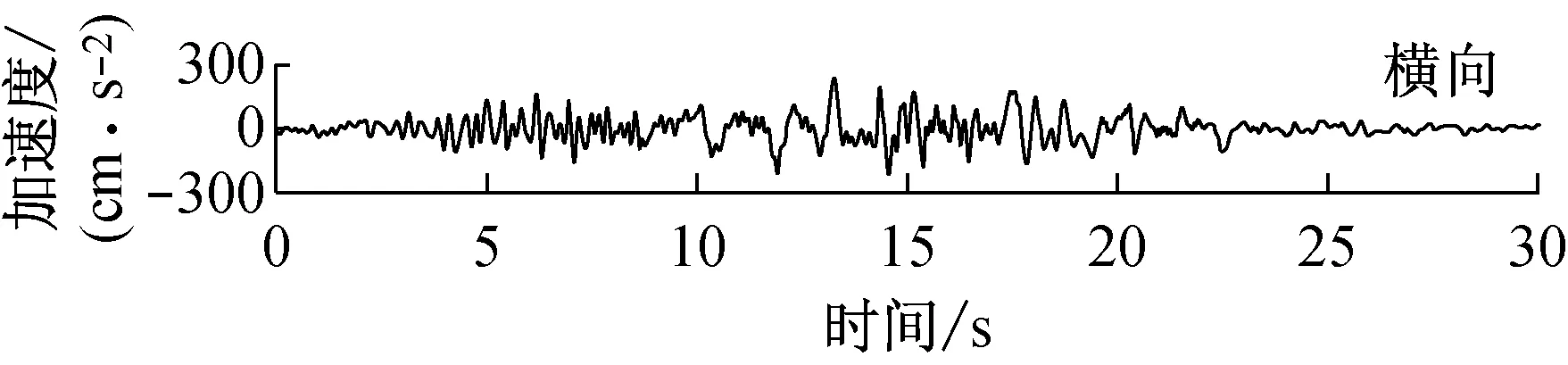
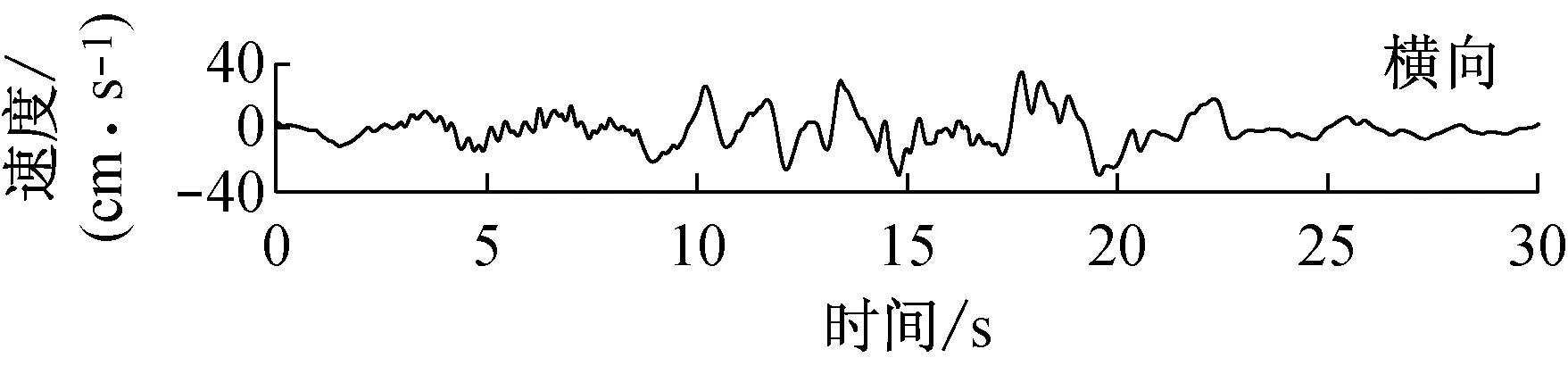
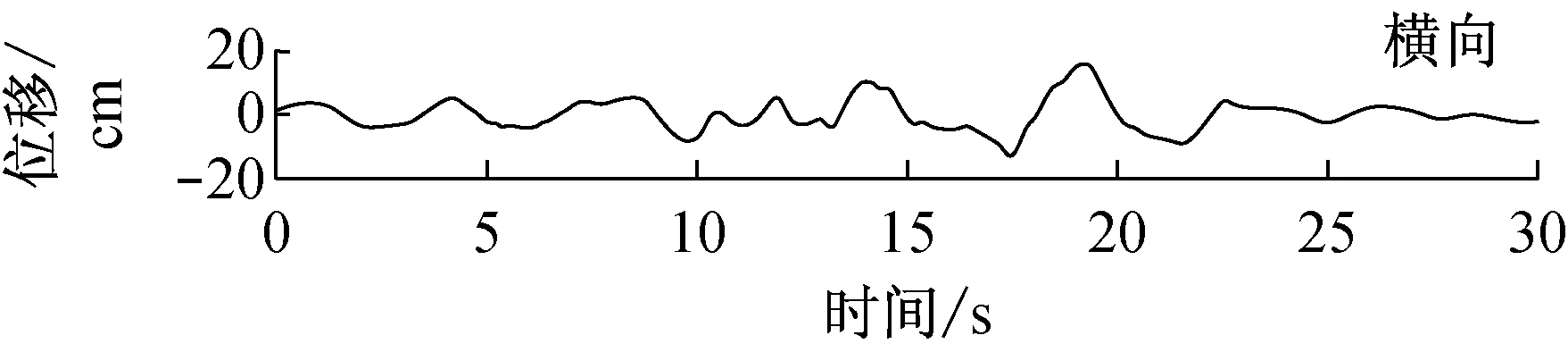
b 目标傅里叶幅值谱:M=6.5,R=20 km,p=0.5,s=0;x=4 km; 频带: 0.125～25 Hz

图6 合成地震动平动分量的加速度、速度和位移时程

Fig.6 Synthetic accelerations, velocities and displacements of translational components

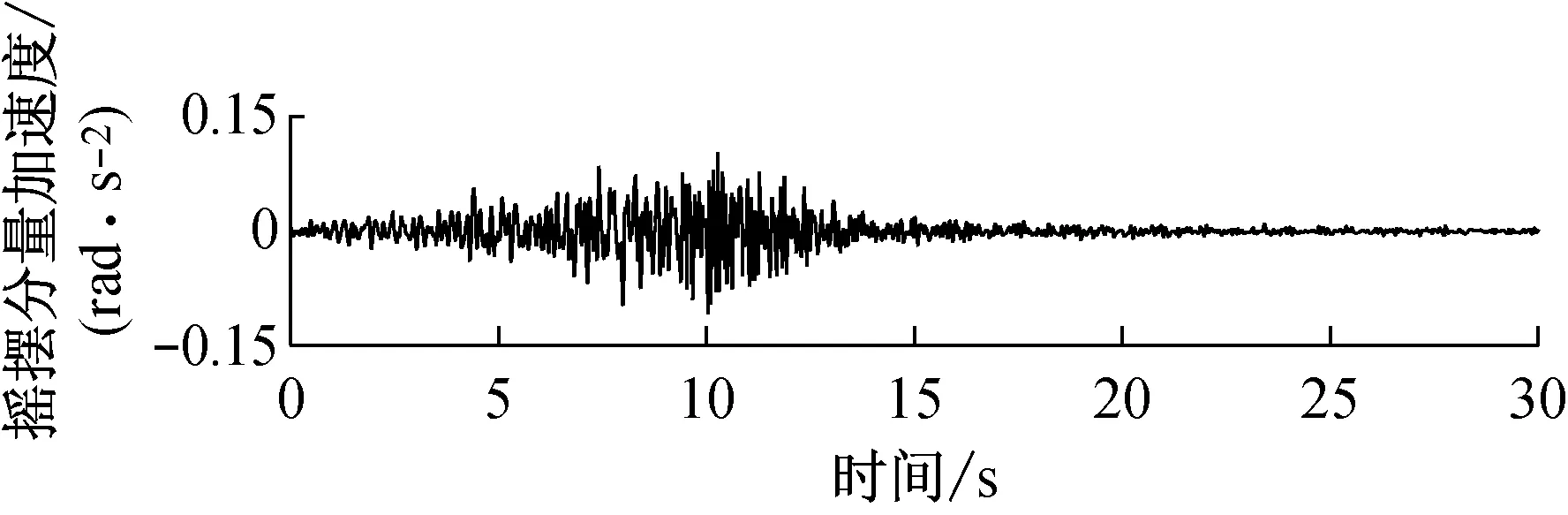
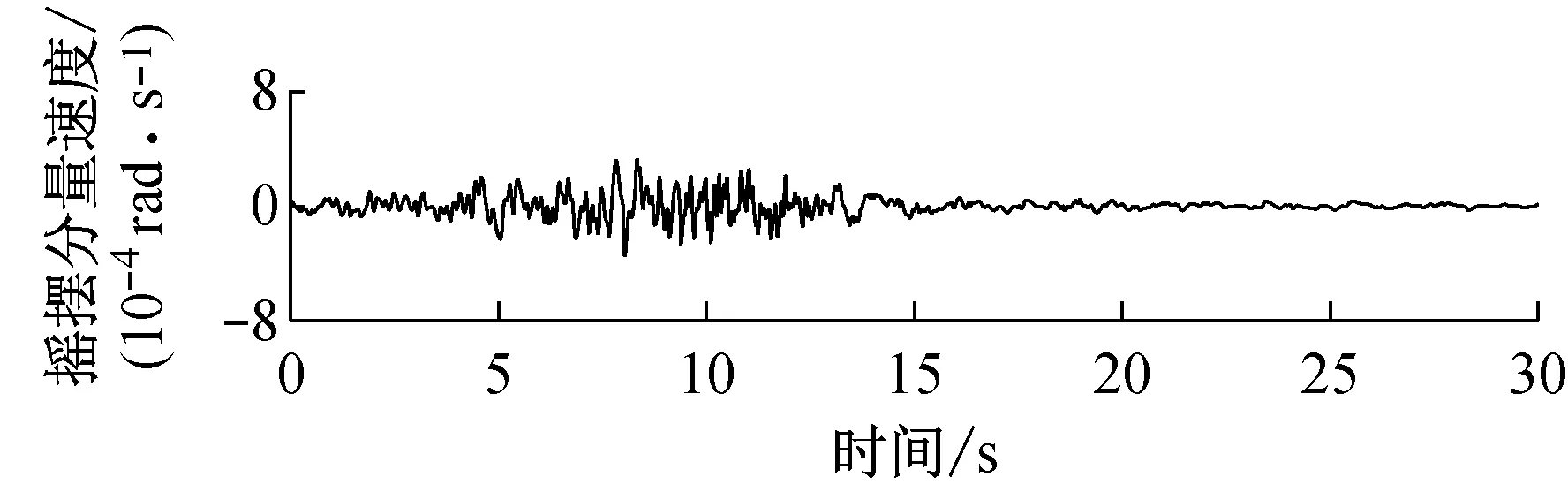
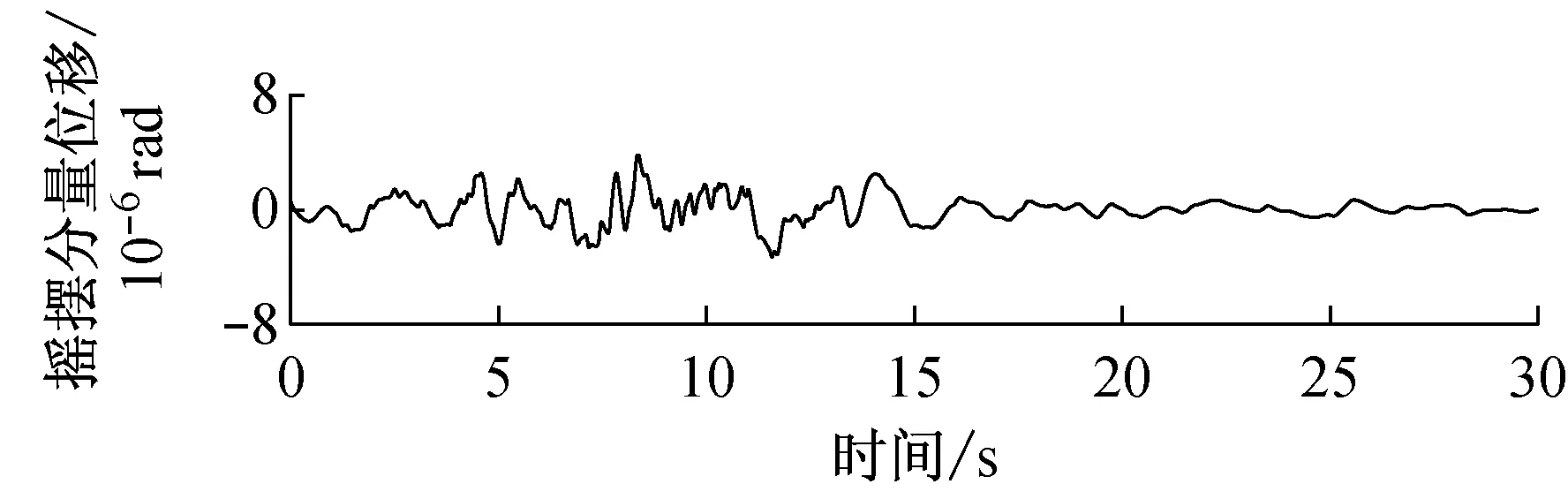
a 目标傅里叶幅值谱:M=6.5,R=10 km,p=0.5,s=0;x=4 km, 频带: 0.125～25 Hz

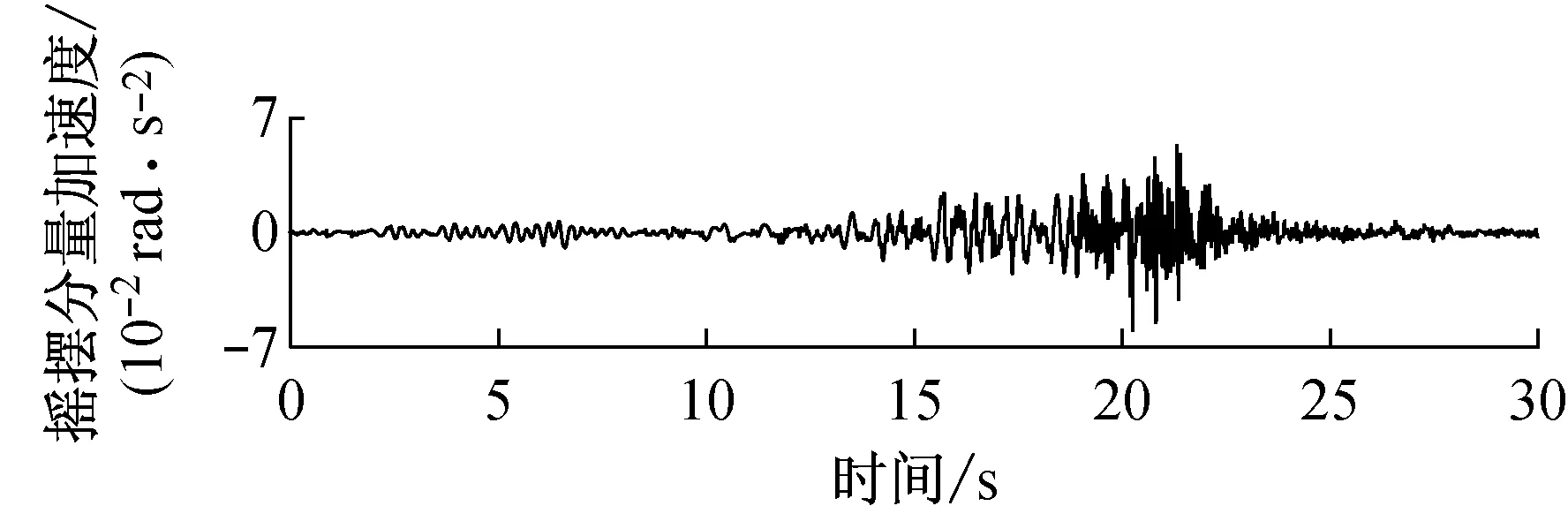
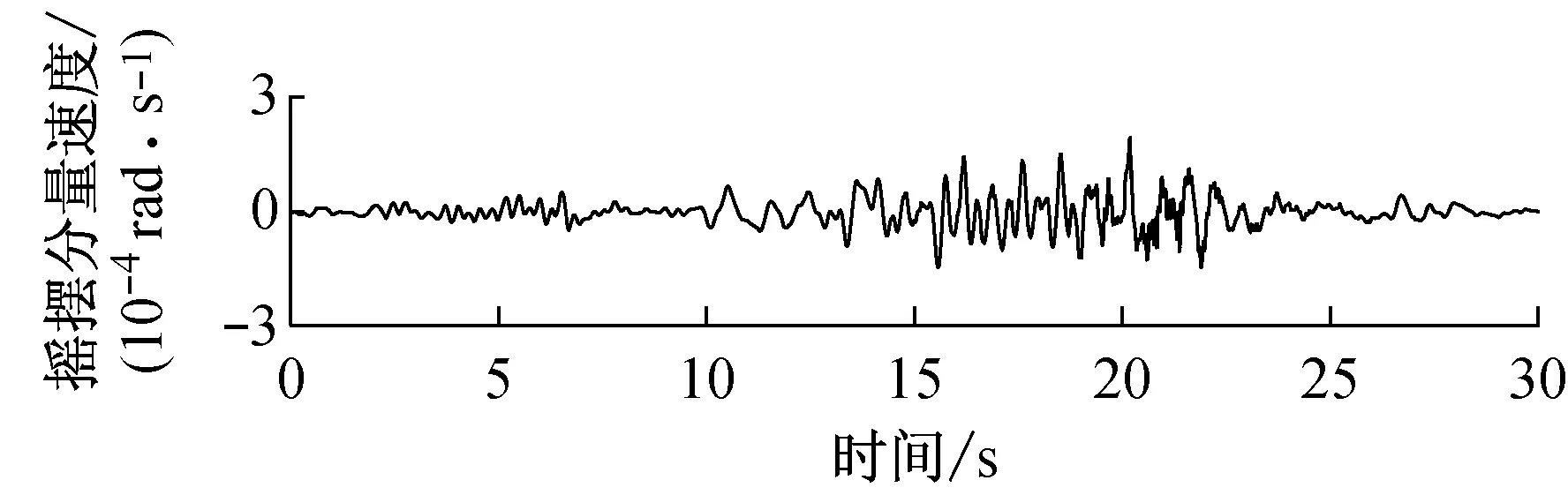
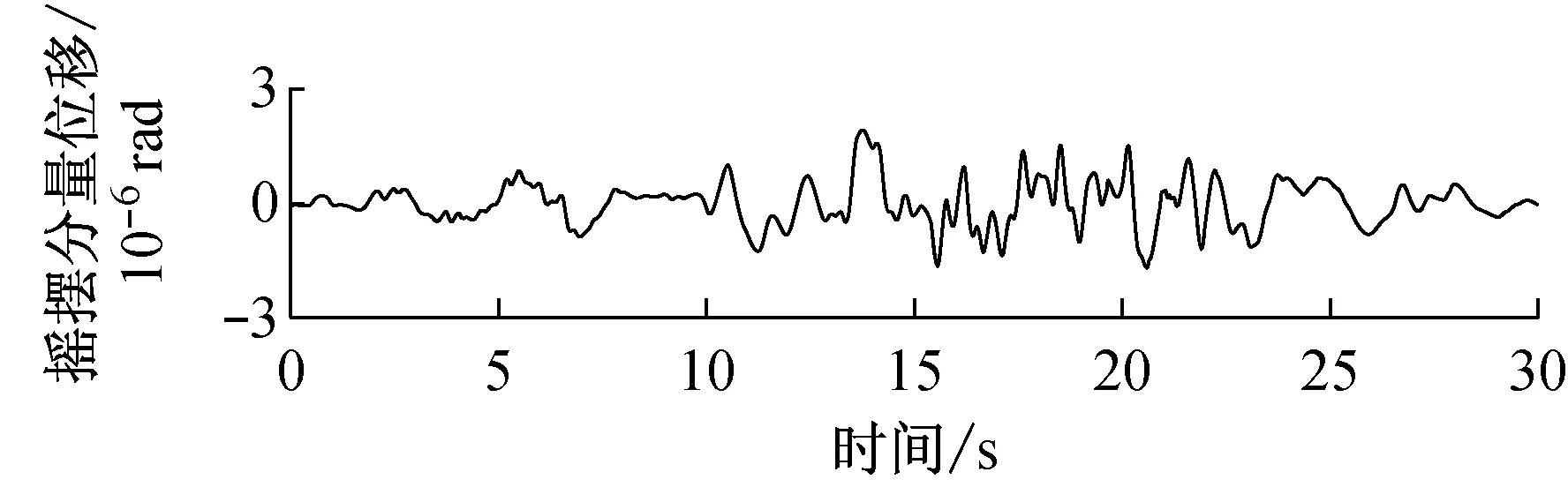
b 目标傅里叶幅值谱:M=6.5,R=20 km,p=0.5,s=0;x=4 km, 频带: 0.125～25 Hz

图7 合成地震动摇摆分量ψ12的加速度、速度和位移时程

Fig.7 Synthetic accelerations, velocities and displacements of rocking componentsψ12

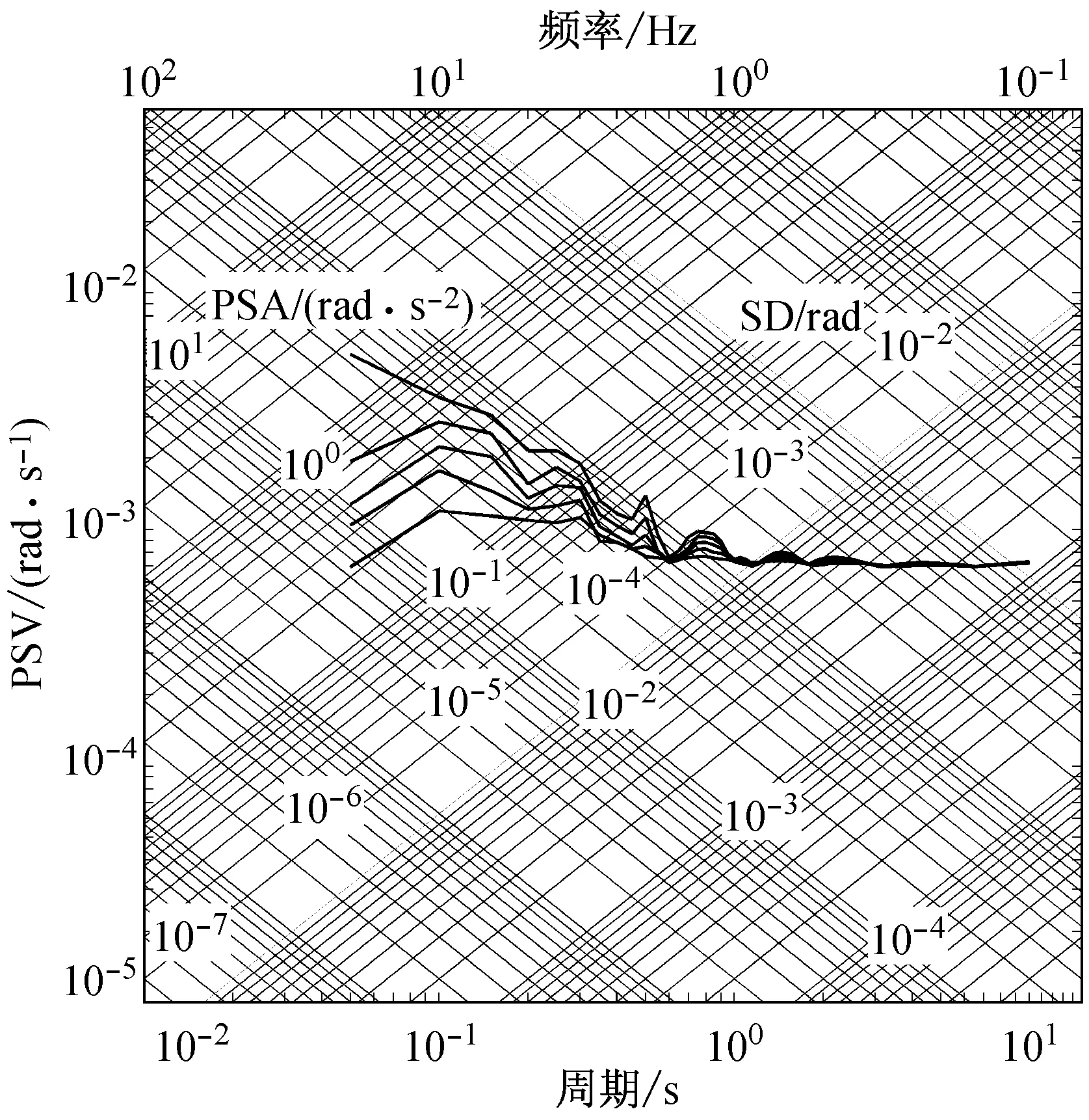
a 震中距R=10 km

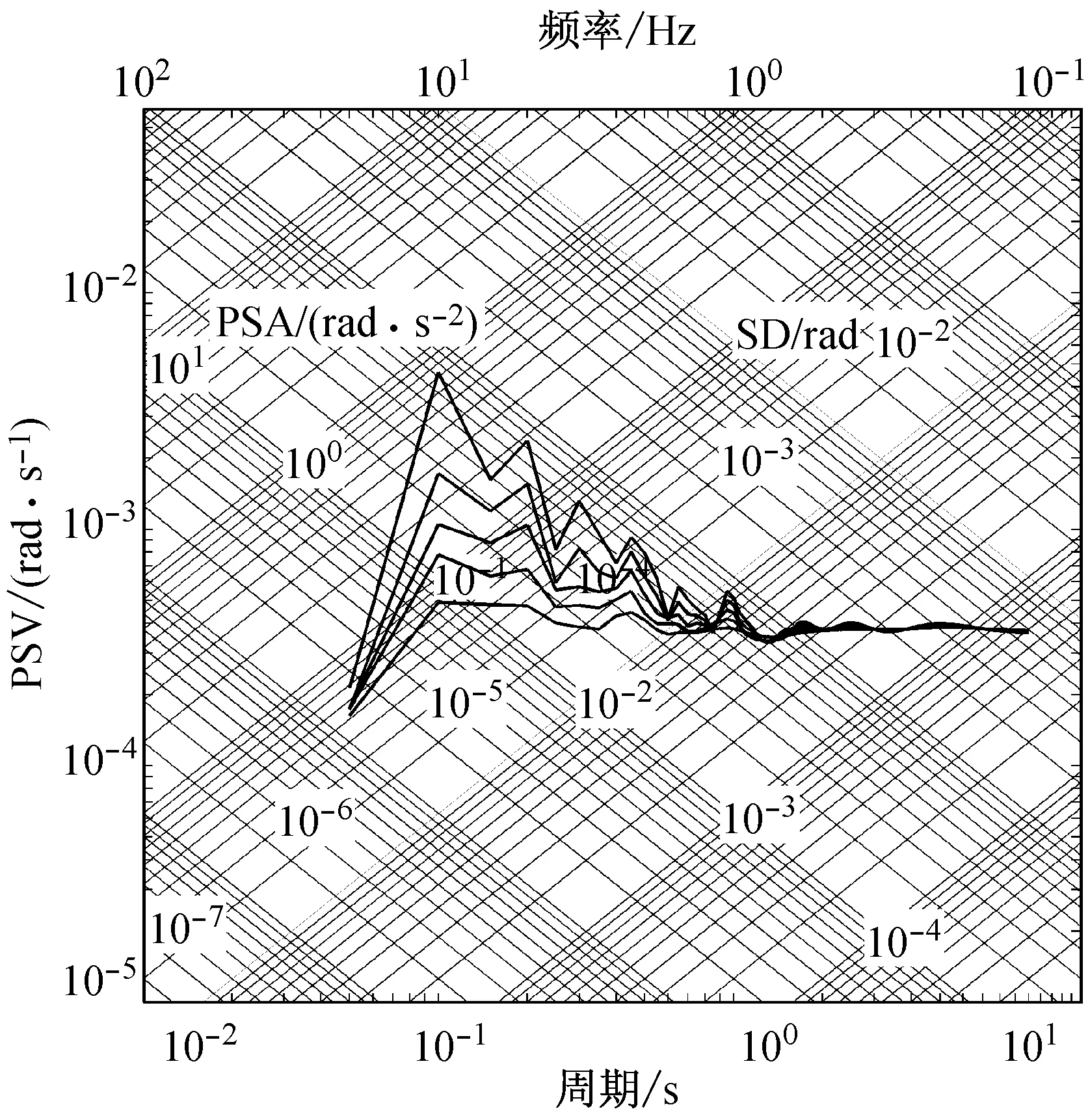
b 震中距R=20 km

4 结论

(1) 本文的合成方法考虑了地震动相位角的随机性，因此合成的地震动集合也是随机的；对于每个集合不同点处地震动的相移是基于相应波型的相速度计算而得的.

(2) 地表某点的地震动摇摆分量的加速度、速度和位移时程可由合成的地震动平动分量获取；运用弹性波动理论，给出了地震动平动分量与摇摆分量之间的关系，此时地震动摇摆分量可反映给定的地震震级、震源深度、震中距、场地类别和超越概率等的物理特性.

(3) 在水平成层的半无限弹性空间中，地震的目标傅里叶幅值谱、面波传播的物理模型和具体场地类型等，均为理想化的设定，这与实际情况有一定的差异，需进一步研究.虽然地震动摇摆分量的幅值明显小于平动分量的幅值，但是对于较大尺度结构(如高层建筑物，桥梁，管道和传输系统等)的地震响应具有明显的扭转效应，在结构设计中需要考虑上述地震加速度时程.因此，根据地震震级M、震中距R和场地类别s等设定条件，合成供实际工程应用的地震动摇摆分量，具有一定的工程应用价值.

[1] Li H N, Sun L Y, Wang S Y. Improved approach for obtaining rotational components of seismic motion[J]. Nuclear Engineering & Design, 2004, 232(2):131.

[2] Awad A M, Humar J L. Dynamic response of buildings to ground rotational motion[J]. Canadian Journal of Civil Engineering, 2011, 11(1):48.

[3] Hart G C, Jr D J, Lew M. Torsional response of high-rise buildings[J]. Journal of the Structural Division, 2014, 101(2):397.

[4] Graizer V M. Effect of tilt on strong motion data processing[J]. Soil Dynamics & Earthquake Engineering, 2005, 25(3):197.

[5] Bouchon M, Aki K. Strain, tilt, and rotation associated with strong ground motion in the vicinity of earthquake faults[J]. Bulletin of the Seismological Society of America, 1982, 72(5):1717.

[6] Lee V W, Trifunac M D. Rocking strong earthquake accelerations[J]. Soil Dynamics & Earthquake Engineering, 1987, 6(2):75.

[7] Che W, Luo Q. Time-frequency response spectrum of rotational ground motion and its application[J]. Earthquake Science, 2010, 23(1):71.

[8] 孙士军, 陈国兴. 地面运动转动分量的合成方法[J]. 防灾减灾工程学报, 1998, 18(1):19.

SUN Shijun, CHEN Guoxing. Synthesis method for estimation of rotation components of ground motion[J]. Journal of Disaster Prevention and Mitigation Engineering, 1998, 18(1):19.

[9] 何超, 罗奇峰, 洪钟. 关于地震动转动分量的研究[J]. 地震研究, 2011, 34(1):81.

HE Chao, LUO Qifeng, HONG Zhong. Brief discussion on the study of the seismic rotational components[J]. Journal of Seismological Research, 2011, 34(1):81.

[10] 魏文晖, 薛广文, 张迪,等. 基于小波分析的地震动转动分量研究[J]. 岩土工程学报, 2015, 239(7): 1241.

WEI Wenhui, XUE Guangwen, ZHANG Di，etal. Rotational components of ground motion based on wavelet analysis[J]. Chinese Journal of Geotechnical Engineering, 2015, 239(7): 1241.

[11] Graizer V, Kalkan E. Prediction of spectral acceleration response ordinates based on PGA attenuation[J]. Earthquake Spectra, 2009, 25(1):39.

[12] Buchen P W, Ben-Hador R. Free-mode surface-wave computations[J]. Geophysical Journal International, 2007, 124(3):869.

[13] Wong H L, Trifunac M D. Synthesizing realistic strong motion accelerograms[R]. Los Angeles: University of Southern California, 1978.

[14] Todorovska M I, Trifunac M D, Lee V W,etal. Synthetic earthquake ground motions on an array[J]. Soil Dynamics and Earthquake Engineering, 2014, 48(5):234.

[15] Trifunac M D. Q and high-frequency strong motion spectra[J]. Soil Dynamics and Earthquake Engineering, 1994, 13(3):149.

[16] Trifunac M D, Todorovska M I. Duration of strong ground motion during Northridge, California, Earthquake of January 17, 1994[J]. Soil Dynamics & Earthquake Engineering, 2012, 38(7):119.

[17] Jalali R S, Trifunac M D. Response spectra for near-source, differential, and rotational strong ground motion[J]. Bulletin of the Seismological Society of America, 2009, 99(2B):1404.

Synthetic Rocking Accelerograms of Earthquake Ground Motions

YAO Zhenya, JIN Guofang

(College of Civil Engineering, Tongji University, Shanghai 200092, China)

The influence of wavelength and Fourier amplitude spectra of the body wave (P and SV wave), together with its interference surface waves (Rayleigh wave) on the the rocking components of earthquake motions was explored, and the synthetic formula of rocking components of earthquake motions was obtained. The dispersion curve of surface wave in given crustal model was obtained based on the elastic-wave-theory and the fastδ-matrix algorithm. Meanwhile the synthetic process of the rocking components of earthquake motions involving incident body and surface waves was explored based on Trifunac’s research. The Trifunac’s composite formula was modified to generate translational components of earthquake motions, relevant to earthquake magnitudeM, epicentral distanceR, and site conditions. Then rocking components of earthquake motions of a spot of ground surface were generated according to the differential frequency of body and surface waves, and corresponding tripartite response spectrum was given.

rocking components of earthquake motions; elastic-wave-theory; target Fourier amplitude spectra; incident body and surface waves; tripartite response spectrum

2015-10-16

姚振亚(1984—)，男，博士生，主要研究方向为工程抗震与防灾，结构抗震鉴定与加固.E-mail：yzy0614@163.com

P315.9

A