桥梁极值应力的改进高斯混合粒子滤波器动态预测

樊学平， 刘月飞， 吕大刚

(1.兰州大学 西部灾害与环境力学教育部重点实验室，甘肃 兰州 730000；2.兰州大学 土木工程与力学学院，甘肃 兰州 730000；3.哈尔滨工业大学 结构工程灾变与控制教育部重点实验室，黑龙江 哈尔滨 150090；4.哈尔滨工业大学 土木工程学院，黑龙江 哈尔滨 150090)



桥梁极值应力的改进高斯混合粒子滤波器动态预测

樊学平1,2， 刘月飞1,2， 吕大刚3,4

(1.兰州大学 西部灾害与环境力学教育部重点实验室，甘肃 兰州 730000；2.兰州大学 土木工程与力学学院，甘肃 兰州 730000；3.哈尔滨工业大学 结构工程灾变与控制教育部重点实验室，黑龙江 哈尔滨 150090；4.哈尔滨工业大学 土木工程学院，黑龙江 哈尔滨 150090)

为合理地动态预测在役桥梁的极值应力信息，应用桥梁健康监测(BHM)系统的长期日常监测极值应力数据，建立非线性动态模型，引入扩展卡尔曼滤波器(EKF)与高斯混合粒子滤波器(GMPF)相结合的改进高斯混合粒子滤波器(IGMPF)预测算法，对监测极值应力的一步向前预测分布参数及其状态变量的后验分布参数进行预测分析, 并进行了实例验证.IGMPF不仅可以得到实测极值应力状态的合理重要性函数，还可以解决传统预测方法的短期性和精度不高的问题，为实际BHM系统的动力响应预测提供了理论基础.

监测极值应力数据； 非线性动态模型； 扩展卡尔曼滤波器； 高斯混合粒子滤波器； 改进高斯混合粒子滤波器

为保障桥梁的安全性、适用性、耐久性，避免灾难性事故的发生，需要对桥梁进行健康监测、动力响应预测等.在役桥梁结构的健康监测已成为各国政府、科研机构的投资和研究热点.欧进萍院士在2002年提出：结构健康监测(structural health monitoring，SHM)集传感元件、数据采集、动力响应预测等系统于一体，是工程理论发展与综合的象征和现代结构实验技术的集中体现.

目前，SHM的研究成果己大量应用于实际工程，国内外很多知名大跨度桥梁均安装了健康监测系统，如日本明石海峡大桥、中国的杭州湾跨海大桥、山东滨州黄河公路大桥等[1].SHM系统既可以监测静力响应、动力响应等信息，还可以利用监测数据预测动力响应.

目前，SHM主要包括两个方面：①研制、安装传感器，获得监测数据.研究主要集中在数据压缩、数据恢复、数据获得技术和系统组装技术等方面[2-3]，目前已处于成熟阶段.②监测信息的应用.如何合理地处理监测数据是SHM领域的主要难点之一，目前大量研究主要集中在模态参数识别、损伤识别、模型修正等领域[4-5].而如何利用监测信息预测结构的动力响应已成为SHM亟待解决的的关键问题之一，它将为桥梁的健康监测、诊断以及预防性养护维修提供必要的理论基础和技术支持.

关于结构性能预测方法，国内外已有许多研究成果，但都存在着一定的局限性，如逐次回归分析方法的静态局限性[6]；时间序列分析方法只适合于随机性的平稳数据[7]；灰色预测模型只适合于强趋势性的数据序列[8]，等等.扩展卡尔曼滤波器(EKF)、高斯混合粒子滤波器(GMPF)以及它们相结合的改进高斯混合粒子滤波器(IGMPF)可以实现信息数据的合理动态预测，已在信息处理、模式识别、无线传感网络等领域取得一些研究成果[9-10]，但在桥梁健康监测、动态响应预测以及结构可靠性预测等领域还未展开大量研究.

基于上述问题，本文首先基于美国I-39北桥(连续钢板梁桥)监测的大量极值应力信息，建立了极值应力的非线性动态模型，然后给出IGMPF预测算法，最后基于动态监测的极值应力信息，采用所建的非线性模型和IGMPF预测算法，实现极值应力的动态预测，并进行了实例验证分析.

1 桥梁监测极值应力的非线性动态模型及其主要参数的确定

1.1 基于监测极值应力的非线性动态模型

美国I-39北桥(连续钢板梁桥)SHM系统在长期运营中积累了大量监测应力信息，本文定义每天监测应力的极大值为监测应力极值信息，由这些极值信息回归得到的二次函数，如式(1)所示，它比线性函数可以更合理地反映应力极值信息的趋势项变化规律，因而可以用来构造状态方程，如式(2)～(3)所示.

(1)

(2)

(3)

式(1)～(3)中：h(t)为由极值信息回归得到的二次函数；a，b和c为监测极值应力的回归系数；t为监测时间，d；θt为第t天的极值应力状态值.

由式(2)可以得到

(4)

式(4)的解为

(5)

由式(3)可以得到

(6)

式(6)的解为

(7)

由式(5)和式(7)可知

(8)

对式(8)进行简化，可以近似转化的状态方程如下：

若a>0，则状态方程为

(9)

(10)

若a<0，则状态方程为

(11)

(12)

基于式(9)～(12)，考虑到监测极值应力变量和状态变量的不确定性，本文所建的非线性动态模型如下：

监测方程为

(13)

式中：N[·]为正态分布；Vt+1为t+1时刻监测误差的方差；T为监测的总时间.

若a>0，则状态方程为

(14)

式中：Wt+1为t+1时刻状态误差的方差.

(15)

若a<0，则状态方程为

(16)

(17)

初始状态信息为

(18)

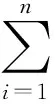
1.2 非线性动态模型主要概率分布参数的确定

非线性动态模型中存在的主要概率分布参数有Vt+1,Wt+1,mt和Ct，确定这些参数的方法如下.

本文模型监测修正的时间间隔为1 d；观测误差的方差Vt+1可以通过对随机荷载效应数据(监测应力数据)采用五点三次平滑法进行平滑处理获得趋势项随机数据与随机荷载效应数据之间的差进行方差估计；状态误差的方差Wt+1可以由初始状态信息的方差结合折扣因子近似确定.根据文献[9]，Wt+1可由下式确定：

(19)

式中：δt-1为时变折扣因子.参考由文献[9]可知，δt-1随状态变量的修正方差增大而减小,但变化范围为0.95～0.98.

对t时刻以及之前的随机荷载效应数据进行五点三次平滑处理，滤去高频随机信号，得到低频趋势项随机数据，即t时刻的状态变量信息.基于这些状态变量值采用如下方法可以对mt和Ct进行估计.

若状态变量值服从对数正态分布，根据等概率变换原则，则通过式(20)可转化为正态分布，且分布参数分别为μ′与σ′(初始状态信息的平均值与标准差)[9].

(20)

式中：φ(·)为正态概率密度函数；g(·)为样本实际概率密度函数.样本实际概率分布函数为G(·)，且G(x0)=0.05，进而可以得到x0的值.

若状态变量值服从其他的概率分布，则初始状态变量值可利用以下方法近似得到N个正态分布的加权组合：

(1) 根据核密度估计方法，历史荷载效应样本的实际概率分布函数F(x)可近似为g(x)，即

(21)

式中：x为历史荷载效应数据.

(2) 由于任何的荷载效应数据概率分布都可以由有限的N个正态分布加权组合得到，所以

(22)

(3) 根据最小离差平方和方法(OLS)可以得到拟合的有限个正态分布的分布参数，即

(23)

式中:有限个正态分布的分布参数可以通过OLS的优化计算方法得到，即当FOLS→min，可以得到正态分布的优化分布参数.

2 基于非线性动态模型的IGMPF预测算法

基于所建立的非线性动态模型，采用条件概率法和贝叶斯方法，可得系统状态θt+1的先验概率分布为

(24)

式中：p(θt+1|θt)可由式(14)～(18)计算得到；p(θt|Dt)可由式(18)近似计算得到.

观测值的一步向前预测分布为

(25)

式中：p(yt+1|θt+1)可由式(13)和式(18)计算得到.

系统状态θt+1的后验概率分布为

(26)

由式(1)～(3)可知，要采用GMPF算法预测观测值的一步向前预测分布p(yt+1|Dt)和系统状态θt+1的后验概率分布p(θt+1|Dt+1)，还必须得到合适的重要性概率密度函数.

2.1 p(θt+1|Dt+1)基于EKF的近似重要性概率密度函数

基于式(18)，t时刻的状态变量概率密度函数为

(27)

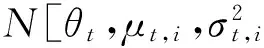
由于观测误差和状态噪音均服从单一正态分布，结合EKF[10]与式(14)～(18)，式(24)可进一步转化为

(28)

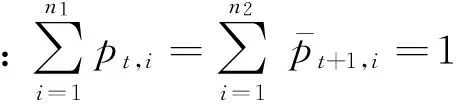
(29)

得到yt+1之后，基于式(13)和式(28)可得

(30)

式中：Ck=∫p(θt+1|Dt)p(yt+1|θt+1)dθt+1.

采用式(28)和式(30)可得

p(θt+1|Dt+1)≈

(31)

式中：

(32)

2.2 基于EKF与GMPF的IGMPF预测算法

由式(13)～(18)和式(24)～(32)，可得基于非线性动态模型的IGMPF预测算法如下.

2.2.1t+1时刻状态变量的后验概率分布

由式(29)可得t+1时刻状态变量的先验概率分布为

(33)

得到t+1时刻的监测值之后，利用式(31)，p(θt+1|Dt+1)可以近似求解.

(34)

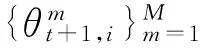
(35)

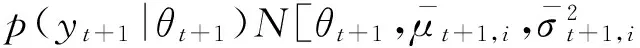
(36)

(37)

修正的粒子权重为

(38)

最后可得t+1时刻状态变量的后验概率分布为

(39)

2.2.2t+2时刻状态变量的先验概率分布

基于式(28)，(33)和(39), 可得

p(θt+2|Dt+1)≈

(40)

采用高斯粒子滤波器[10-11]，p(θt+2|Dt+1)的递推修正如下：

(41)

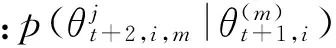
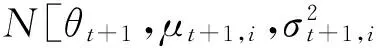
(42)

修正的粒子权重为

(44)

进而可得t+2时刻状态变量的先验概率分布为

(45)

2.2.3t+2时刻观测变量的一步向前预测分布

利用式(13)，(25)和(45)可得

p(yt+2|Dt+1)=∫p(θt+2|Dt+1)p(yt+2|θt+2)dθt+2≈

(46)

一步向前预测分布的均值和方差分别为

(47)

一步向前预测的预测精度为

(48)

对于实测监测极值应力数据而言，方差σM=0.而本文采用IGMPF算法预测得到的极值应力数据由于考虑到数据的随机性和不确定性，所以σM≠0.

基于上述IGMPF预测算法，可得极值应力的动态预测方法如图1所示.

图1 极值应力的动态预测框架

3 算例分析

美国I-39北桥[12-14]建于1961年，是一座五跨连续钢板梁桥，总长度为188.81 m，桥梁监测项目包括结构特定构件的应力和应变评估等.关于检测项目的详细内容和目的，参见文献[13].此项目对横向第二跨钢板的跨中梁底极值应力进行了90 d的监测，监测数据只考虑了由车辆荷载、温度荷载、收缩徐变和结构变化引起的应力的变异性，由钢板和混凝土恒载引起的应力信息不包括在监测数据里面.现利用前83 d的监测极值应力数据，建立极值应力的非线性动态模型及其IGMPF预测算法，然后基于第83天到第89天的监测极值应力数据，对第84天到第90天的极值应力进行动态预测.

采用前83 d监测极值应力拟合得到的二次函数为

mt=-0.001t2+0.055t+24.93

(49)

式中：mt近似为第t天的极值应力状态值.

为了得到初始状态信息的分布参数，对前83 d的监测极值应力数据进行了五点三次平滑处理，处理之后的数据近似作为状态数据，如图2所示.对状态数据进行K-S检验，可知初始状态信息的分布信息如式(53)所示.图3显示了初始状态分布曲线基于不同监测极值应力信息修正的状态分布曲线，可看出基于不同的监测极值应力信息，采用IGMPF修正预测得到的状态分布曲线不同，从而可知建立动态模型来动态修正预测极值应力状态是必要的.

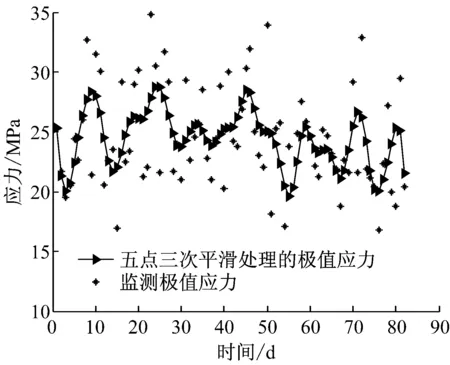
图2 平滑处理后的极值应力与监测极值应力对比

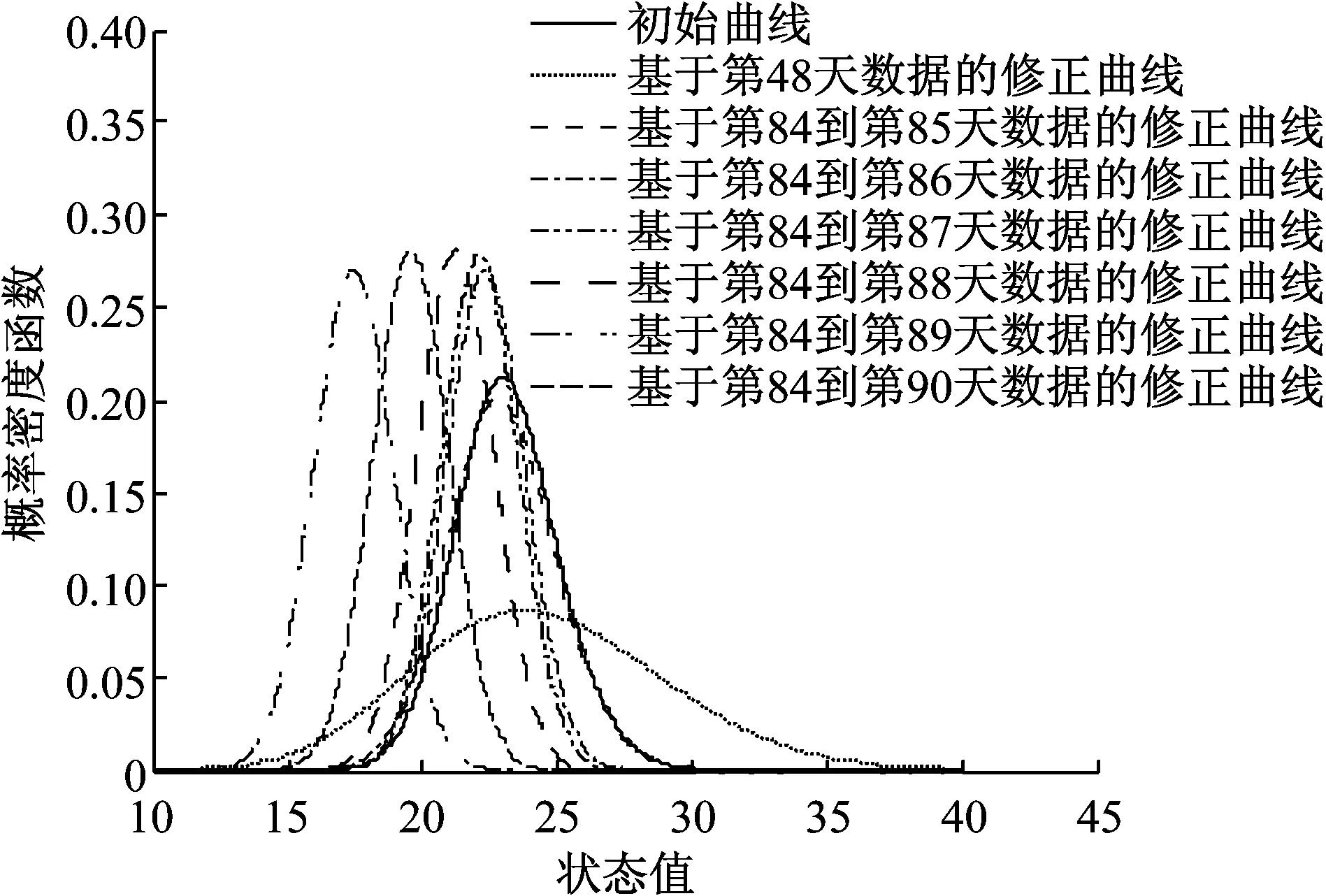
图3 初始状态修正前后的概率密度函数

利用式(1)～(18)和式(49)，可建立非线性动态模型.

监测方程为

(50)

式中：yt+1为t+1时刻的监测极值应力；θt+1为t+1时刻的状态值；νt+1是监测误差；Vt+1=21.75,可以利用监测极值数据与平滑之后的趋势项随机信息近似估计得到.

状态方程为

ωt+1～N[0,Wt+1],t≤24

(51)

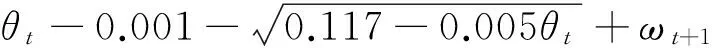
ωt+1～N[0,Wt+1],t>24

(52)

式中:ωt+1为状态误差.

初始状态信息为

0.5LN[3.18, 0.192]≈

0.5N[24.56, 4.672]+

0.5N[23.17, 3.352]

(53)

式中：N[·]为正态概率分布;LN[·]为对数正态概率分布.

利用式(50)～(53)和式(33)～(48)，基于第83天到第89天的监测极值应力数据，预测得到的第84天到第90天的极值应力数据与预测精度，如图4和图5所示.从图4可知,预测得到的极值应力满足监测极值应力的变化规律，两者结果近似相等.图5显示出随着监测极值应力的不断修正，非线性动态模型和IGMPF算法的预测精度越来越好，进一步验证了本文所建非线性动态模型和IGMPF预测算法的合理性.

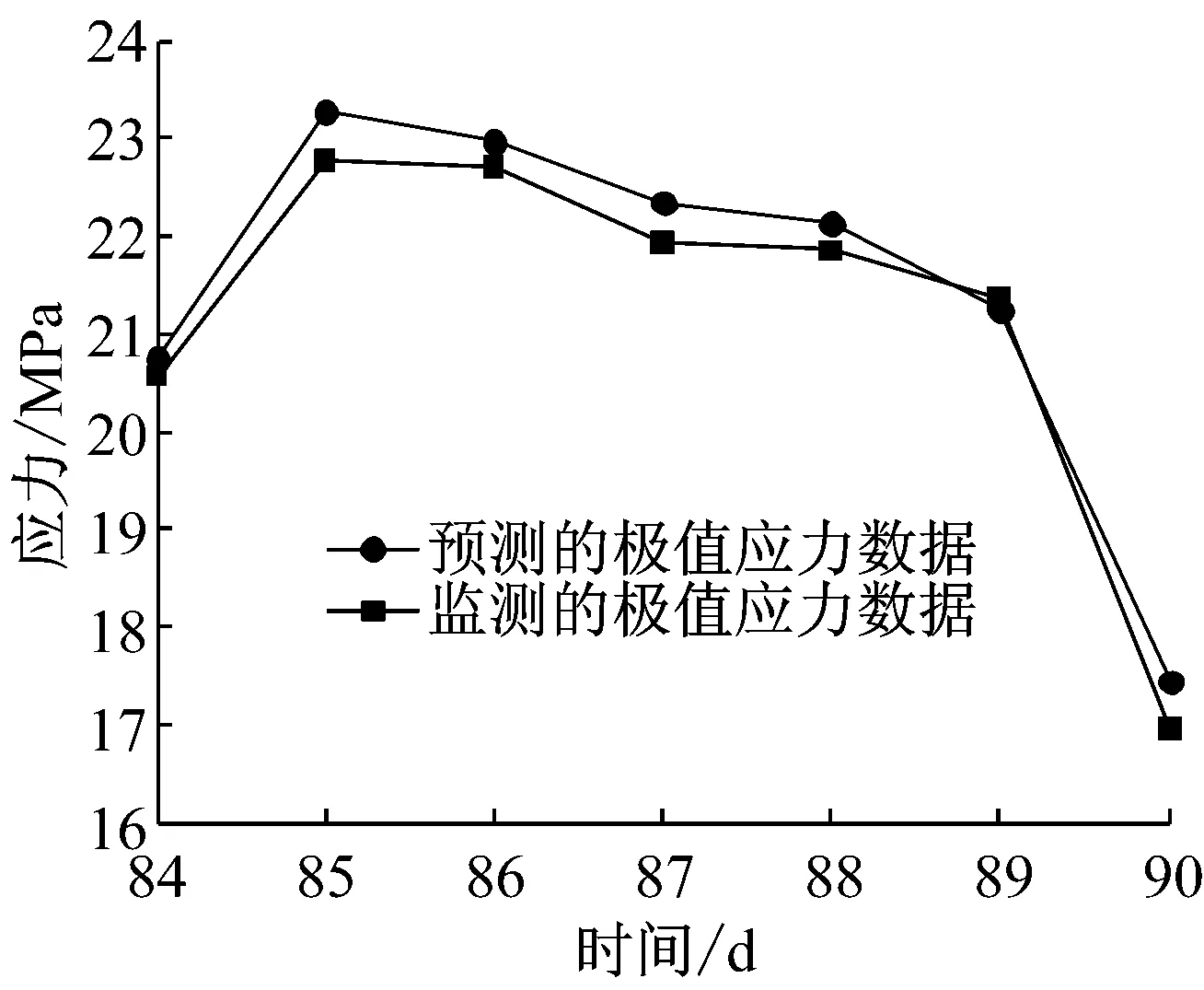
图4 极值应力的预测值和监测值

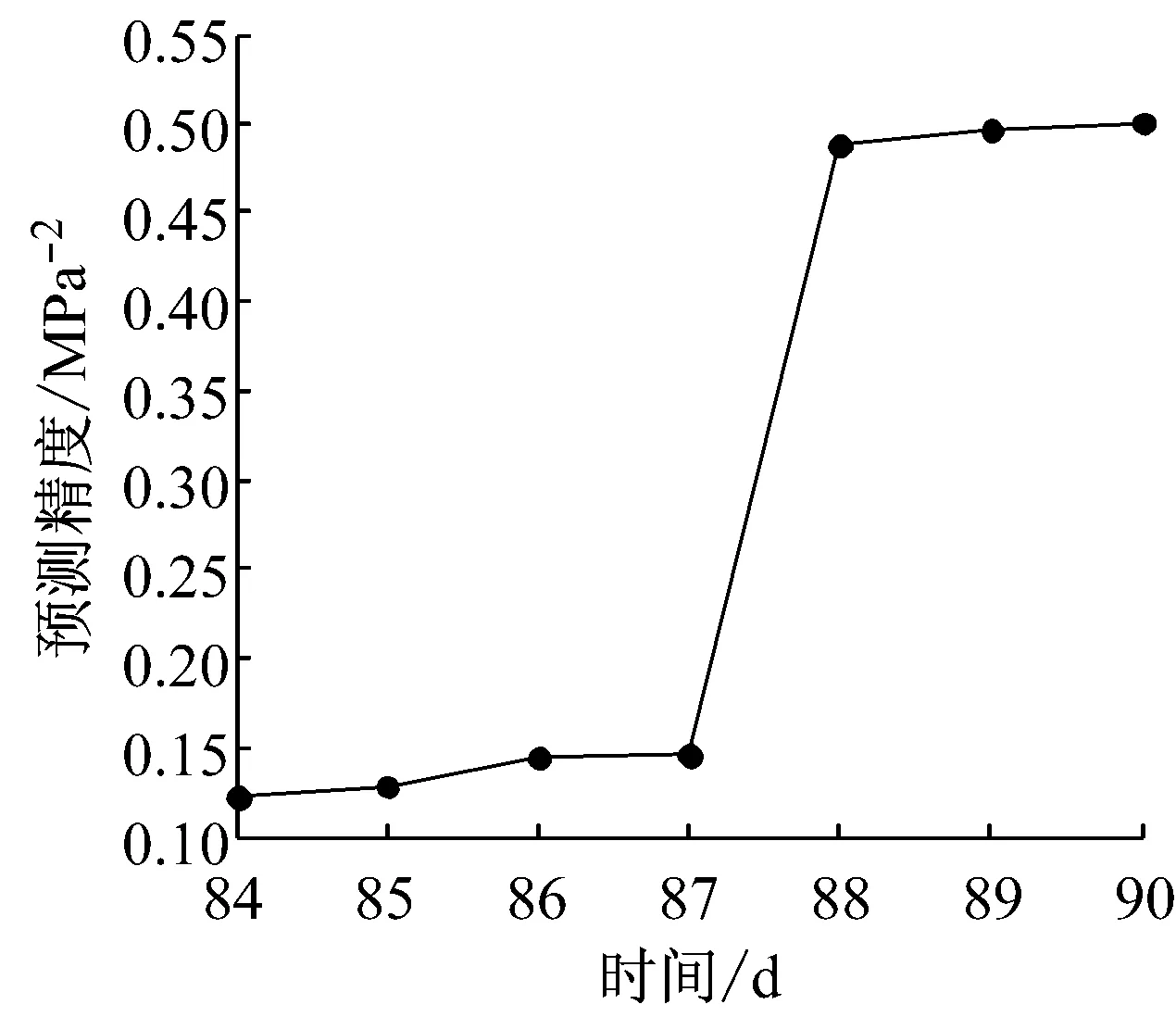
图5 非线性动态模型的预测精度

4 结论

本文首次基于监测极值应力信息给出非线性动态模型与相对应的IGMPF预测算法，并通过实际工程进行了验证.从分析结果可以看出：

(1) 预测的极值应力与监测得到的极值应力近似相等.

(2) 基于监测极值应力数据的不断修正，所建的非线性动态模型和IGMPF算法的预测精度越来越好，更加验证了本文所建非线性动态模型和IGMPF预测算法的合理性与适用性.

基于三次函数和多次函数的非线性动态模型、初始监测应力数目大小(初始粒子数目)以及动态监测极值应力数据对IGMPF预测精度的影响规律有待进一步研究.

[1] 李星新. 基于健康监测的钢桥面板疲劳寿命评估[D]. 长沙: 中南大学, 2012.

LI Xingxin. Fatigue life evaluation of orthotropic steel plate based on health monitoring[D]. Changsha: Central South University, 2012.

[2] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655.

[3] 李惠, 周文松, 欧进萍,等. 大型桥梁结构智能健康监测系统集成技术研究[J]. 土木工程学报, 2006, 39(2): 46.

LI Hui, ZHOU Wensong, OU Jinping,etal. A study on system integration technique of intelligent monitoring systems for soundness of long-span bridges[J]. China Civil Engineering Journal, 2006, 39(2): 46.

[4] 宗周红, 周儒勉, 郑沛娟. 基于健康监测的桥梁结构损伤预后和安全预后研究进展及挑战[J]. 中国公路学报, 2014, 27(12), 46.

ZONG Zhouhong, ZHOU Rumian, ZHENG Peijuan. Damage and safety prognosis of bridge structures based on structural health monitoring: progress and challenges[J]. China Journal of Highway and Transport, 2014, 27(12), 46.

[5] 魏锦辉, 任伟新. 基于响应面方法的桥梁静动力有限元模型修正[J]. 公路交通科技, 2015, 32(2): 68.

WEI Jinhui, REN Weixin. Static and dynamic bridge finite element model updating based on response surface method[J]. Journal of Highway and Transportation Reasearch and Development, 2015, 32(2): 68.

[6] 钟才根, 丁文其, 王茂和, 等. 神经网络模型在高速公路软基沉降预测中的应用[J]. 中国公路学报, 2003, 16(2): 31.

ZHONG Caigen, DING Wenqi, WANG Maohe,etal. Application of artificial neural network in settlement prediction of highway soft foundation[J]. China Journal of Highway and Transport, 2004, 16(2): 31.

[7] 兰孝奇, 杨永平, 黄庆, 等. 建筑物沉降的时间序列分析与预报[J]. 河海大学学报: 自然科学学报, 2006, 34(4):426.

LAN Xiaoqi, YANG Yongping, HUANG Qing,etal. Analysis and prediction of time series for building settlement[J]. Journal of Hohai University: Natural Sciences, 2006, 34(4): 426.

[8] 张仪萍, 俞亚南, 张士乔, 等. 沉降预测中的灰色模型理论与Asaoka法[J]. 系统工程理论与实践, 2002, 22(9): 141.

[9] 樊学平. 基于验证荷载和监测数据的桥梁可靠性修正与贝叶斯预测[D]. 哈尔滨, 哈尔滨工业大学, 2014.

FAN Xueping. Bridge reliability updating and Bayesian prediction based on proof loads and monitored data[D]. Harbin: Harbin Institute of Technology, 2014.

[10] 胡士强, 敬忠良. 粒子滤波原理及其应用[M]. 北京: 科学出版社, 2010.

HU Shiqiang, JING Zhongliang. Particle filtering theory and its application[M]. Beijing: Science Press, 2010.

[11] Peng Y H, Liu Y F, Miu D,etal. Application of gaussian mixture particle filter on state estimation[J]. Journal of Projectiles Rockets Missiles & Guidance, 2007, 27(1): 271.

[12] Frangopol D M, Strauss A, Kim S Y. Use of monitoring extreme data for the performance prediction of structures: general approach [J]. Engineering Structures, 2008, 30: 3644.

[13] Strauss A, Frangopol D M, Kim S Y. Use of monitoring extreme data for the performance prediction of structures: Bayesian updating [J]. Engineering Structures, 2008, 30: 3654.

[14] Mahmoud H N, Connor R J, Bowman C A. Results of the fatigue evaluation and field monitoring of the I-39 Northbound Bridge over the Wisconsin River[R]. Bethlehem: Lehigh University, 2005.

Improved Gaussian Mixed Particle Filter Dynamic Prediction of Bridge Monitored Extreme Stress

FAN Xueping1,2, LIU Yuefei1,2, LÜ Dagang3,4

(1. Key Laboratory of Mechanics on Disaster and Environment in Western China of the Ministry of Education, Lanzhou University, Lanzhou 730000, China; 2. School of Civil Engineering and Mechanics, Lanzhou University, Lanzhou 730000, China; 3. Key Laboratory of Structures Dynamic Behavior and Control of the Ministry of Education, Harbin Institute of Technology, Harbin 150090, China; 4. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090, China)

To reasonably and dynamically predict the extreme stress information of in-service bridge, in this paper, the nonlinear dynamic models were built including monitoring equation and state equation with the long-term everyday monitored extreme stress data of bridge health monitoring (BHM) system. Then the improved Gaussian mixed particle filter (IGMPF) prediction algorithm was introduced which was obtained by using extended Kalman filter (EKF) and GMPF. IGMPF can predict one-step forward prediction distribution parameters of monitored extreme stress and the posteriori distribution parameters of extreme stress state variable. Finally, an actual example was provided to illustrate the application and feasibility of the IGMPF algorithm built. The IGMPF prediction algorithm can not only obtain the reasonable importance functions of monitored extreme stress states, but also solve the problems of short-term prediction and low precision of the traditional prediction methods. It provides a theoretical foundation for dynamic response prediction of the actual BHM.

monitored extreme stress data; nonlinear dynamic model; extended Kalman filter; Gaussian mixed particle filter; improved Gaussian mixed particle filter

2016-01-22

国家自然科学基金(51608243)；甘肃省自然科学基金(1606RJYA246)；中央高校基本科研业务费专项资金(lzujbky-2015-300，lzujbky-2015-301)

樊学平(1983—)，男，讲师，工学博士，主要研究方向为桥梁结构安全评定与可靠性预测.

E-mail:fxp_2004@163.com; fanxp@lzu.edu.cn

TU391; TU392.5

A