采用小波变换和高斯过程的肌电信号模型预测

邵辉， 苏芳茵， 程海波

(华侨大学 信息与科学工程学院， 福建 厦门 361021)



采用小波变换和高斯过程的肌电信号模型预测

邵辉， 苏芳茵， 程海波

(华侨大学 信息与科学工程学院， 福建 厦门 361021)

根据表面肌电信号的生物电信号特点，采用小波变换和高斯过程建模的方法对表面肌电信号进行建模和预测.对非线性的表面肌电信号利用拟合能力强大的高斯过程进行建模，预测效果较好，但所需运算时间长.针对其运算时间长的缺点进行改进，将预处理后的表面肌电信号小波分解，对分解后的系数高斯建模，然后重构.实验结果表明：该改进方法在响应时间和预测误差方面效果明显.

表面肌电信号； 高斯过程； 小波变换； 模型预测

表面肌电信号(surface electromyographic signal,sEMG)是人体在运动时骨骼肌产生的电信号在皮肤表面处的叠加，是一种信号微弱、噪声复杂的非线性生物电信号[1].表面肌电信号作为智能手臂和假肢的控制源，其采集和处理要求很高.为了更好地控制机械臂，需要对肌电信号进行建模研究.目前,对其进行建模预测的研究相对较少，而常见的非线性建模方法在实际应用中都或多或少存在问题.高斯过程(Gaussian process,GP)于20世纪90年代进入机器学习领域[2-4]，已成为非线性机器学习领域的研究热点[5-7].它可以很好地避免这些问题，并且具有学习参数少，对处理小样本、高维数、非线性等复杂问题有良好的适应性，且泛化能力强的优点.高斯过程模型应用非常广泛.Williams等[8]率先将高斯过程应用于机器学习领域；Murray-Smith等[9]分析比较了基于蒙特卡罗方法的高斯过程先验模型与多模型方法；Kocijan[10]率先提出了一种将高斯过程模型中的方差引入控制信号的预测控制方法.高斯过程模型善于处理小样本、高维数、非线性等复杂问题.因此,本文首次将高斯过程模型应用到肌电信号的建模,并引入了小波变换(wavelet transform，WT).在高斯过程回归前,对样本集进行小波分解处理，从而减少模型学习的时间以提高预测速度.

1 表面肌电信号高斯过程模型

1.1 表面肌电信号描述

对表面肌电信号的处理方法是肌电信号分析和应用的重要部分，其处理方法的选择很大程度上要考虑肌电信号的产生机理.表面肌电信号的数学模型主要有4种：线型系统模型、双极型模型、集中参数模型和非平稳模型.前3种模型均属于稳态分析，即当肌肉用力恒定的平稳情况；当肌肉用力不均时，肌电信号变化不平稳，可以用非平稳模型表征肌电信号，即

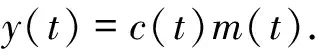
(1)

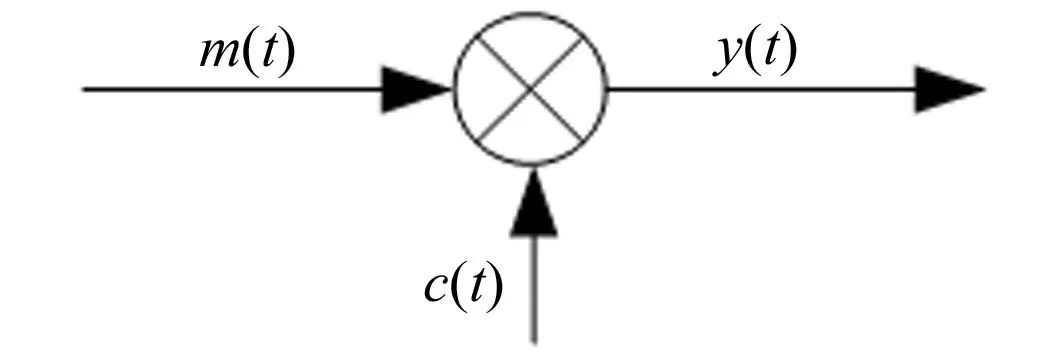
图1 非平稳模型Fig.1 Non-stationary model

式(1)中：c(t)为肌肉收缩程度的调制信号；m(t)为高斯噪声(零均值单位方差)载波信号.表面肌电信号非平稳模型,如图1所示.

1.2 高斯过程建模

高斯过程是在贝叶斯学习理论基础上,发展起来的机器学习方法.它描述了任意有限变量集合的联合密度函数,属于高斯分布的随机过程.对于任意有限随机变量x1,…,xn，其中,n≥1,且为任意整数，与其对应的过程状态f(x1),f(x2),…,f(xn)的联合概率分布服从n维高斯分布.其具体过程可由均值m(x)与协方差函数k(x,x′)确定,即

(2)

给定训练D={(xi,yi)|i=1,2,…,N}，其中，xi∈Rd为输入量，yi∈R是输出向量.则输出向量y由零均值函数m(x)和一个正定的协方差函数k(x,x′)的高斯先验分布组成，即y～N(m,p).

假设输入新的向量x*∈Rd，KN为训练样本的协方差矩阵，则其相应的待预测数据的高斯分布函数为y～N(m*,p*)，其中

(3)

协方差函数的选择没有统一的指导性原则[11]，只需满足对称性和半正定性.目前,常用的协方差函数为平方指数协方差函数，也称为径向基函数(RBF)或高斯函数，其形式为

(4)

式(4)中：x和x′为训练集或测试集中的某个变量组合；σf,l,σn为超参数；δ为符号函数.一般常用极大似然法求解最优超参数[12].

2 小波变换结合高斯模型

高斯过程模型较适用于处理小样本、高维数的问题，而表面肌电信号的样本数量多，其运算量与训练集样本数成正比.因此,在训练集样本数较大时，计算逆矩阵所需要的时间和空间将成倍增大.考虑到这种情况，提出了小波变换结合高斯模型的预测方法.

小波变换的实质是将信号分解为一系列小波函数的叠加，而这些小波函数都是由一个母小波函数经过平移和尺度伸缩得来的.对信号逐步进行时间频率多尺度细化，最终达到高频处时间细分、低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节.

通过多分辨率离散小波变换将肌电信号y(t)分解,即

(5)

式(5)中：φ(t)为尺度函数;ψ(t)为小波函数.则尺度系数和小波系数的表达式为

(6)

(7)

将小波分解产生的尺度系数和小波系数分别进行高斯过程训练，则其相应的待预测数据的高斯分布函数为cj～N(mc,pc),dj～N(md,pd).

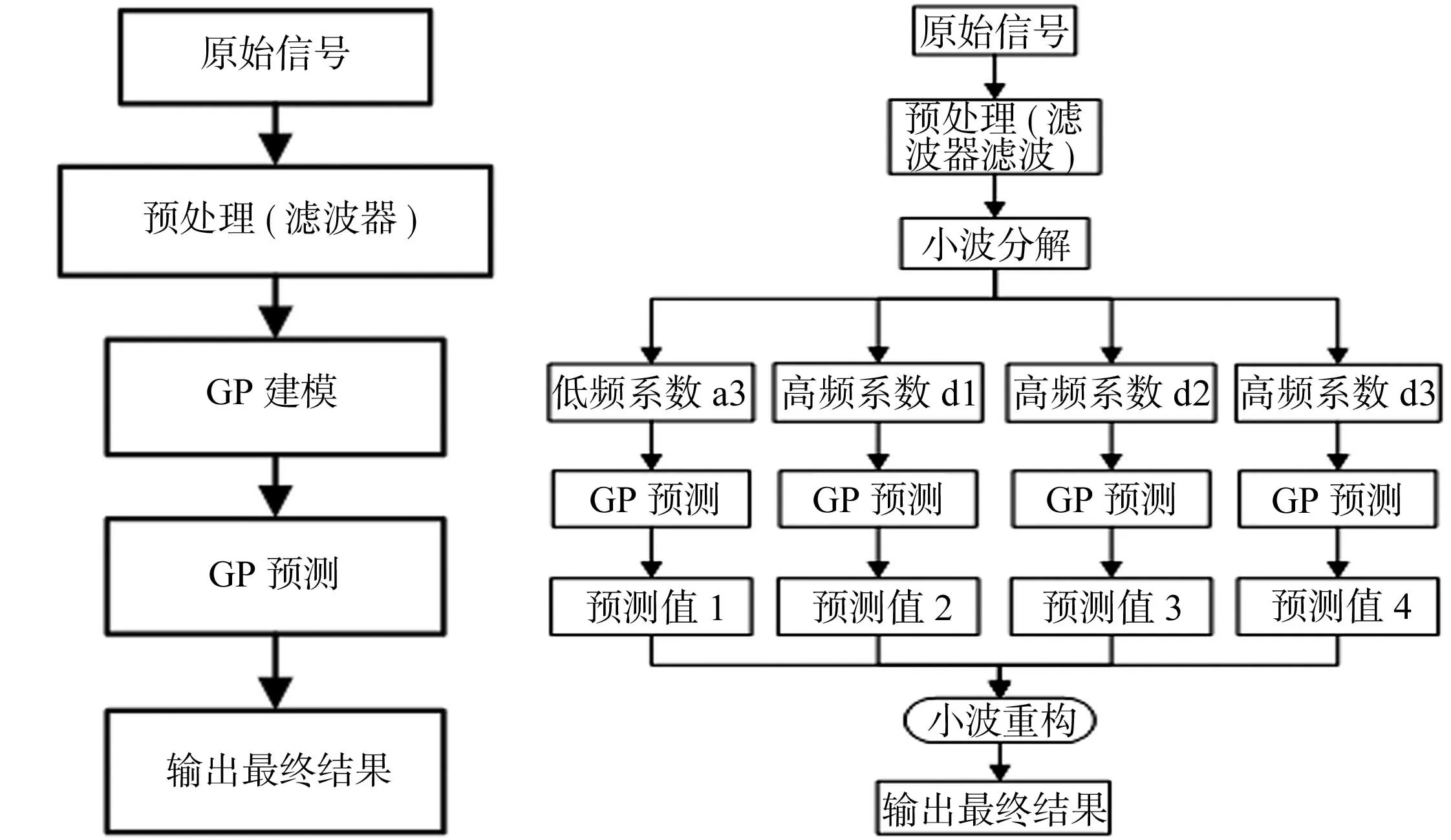
(a) GP预测模型 (b) WT-GP预测组合模型 图2 2种预测模型的对比Fig.2 Comparison of two forecast models

高斯过程模型(GP)和小波变换结合高斯过程(WT-GP)模型在实现过程上不同，具体的模型结构,如图2所示.WT-GP预测模型选用db5小波，对表面肌电信号进行三级分解.db5小波具有较好的正则性，引入的光滑误差不易被察觉，使信号重构过程较光滑.采用小波变换结合高斯过程模型对表面肌电信号进行建模预测.首先，将样本数据进行小波三级分解，第一级可以得到一组低频系数和一组高频系数，继续分解低频部分，以此类推，最终可以得到一组低频系数和三组高频系数，其样本数远小于原来的样本数据;然后,对四组系数分别进行高斯过程回归建模；最后,将每个模型预测的系数重组得到最终的预测结果.

小波变换有多尺度的分析能力，将信号按照不同的尺度分解，降低信号非线性程度.由于非线性程度降低，预测信号的误差减小，因此，提高了预测的精确度.而在小波分解后，低频系数和高频系数的维度明显低于信号本身，所以对其分别求逆的运算量也低于对信号本身求逆.即使低频和高频系数维度相加等于信号自身，但是求逆过程的计算难度确随着矩阵维数成倍增长，故运算时间明显减少.由此可以得出，引入小波后的高斯过程模型预测回归在误差和运算时间上均有优化.

3 实验仿真

3.1 肌电信号采集方案

实验采集设备：表面电极贴、PC机、PCL818L多功能数据采集卡、肌电传感器.实验采用的传感器是日本司机工工程技术公司的TYE-1000M双极型表面电极，其中,包含传感器和放大器，配合使用一次性银/氯化银按钮式电极贴片.

图3 现场信号采集实验图Fig.3 Field signal acquisition experimental picture

采集系统的构建：实验平台采用MATLAB/Simulink/xPC Target的实时环境建立整个肌电信号采集系统，采样频率1 000 Hz，信号主要能量集中在10～500 Hz.现场信号采集实验,如图3所示.实验方案：实验前,上臂经过清洗处理，减少皮肤阻抗，且实验之前未进行激烈运动;实验时，将电极贴片黏在肱二头肌和肱三头肌上，受测者坐在椅子上，手成握拳状，手臂自然下垂，采集两种动作前臂屈伸和前臂旋转各10次.

采集后的肌电信号含有噪声，需要进行滤波.文中选择常用的切比雪夫I型滤波器，其通带下限频率为20 Hz，上限频率为510 Hz；阻带下限为10 Hz，阻带上限为520 Hz；通带衰减小于1 dB，阻带衰减大于60 dB.由此，可确定切比雪夫滤波器阶数为4.

3.2 高斯过程模型预测结果

由理论分析可知：训练集和测试集是两个不同的集合，但这两个集合是由同一个动作产生，因此，这两个集合在本质上是属于同一个样本点集，其预测效果会比较好.如果测试集由其他动作产生，其效果会有所不同.

采集2种动作的肌电信号，从中分别抽取1 500组和1 000组样本数据，选择前一种动作的500组数据作为训练样本，剩下的1 000组数据作为测试样本；而后一种动作的1 000组仅作为测试样本.如此，两个测试集中，一个和样本集属于同一集合，一个属于不同集合.整个学习训练的过程如上叙述，分别对1 000组测试样本进行预测，结果如图4，5所示.

由图4可知：不管测试样本与训练样本是否来自同一动作数集，其预测值与实际值的曲线都几乎相似.图5中:误差曲线和方差曲线的精确度数量级很小.由此可以证明，高斯过程对非线性回归有很强大的学习能力和泛化能力.

由图5可知：属于同一集合测试样本的预测误差曲线优于不同集合测试样本的预测效果；同一集合的预测方差明显低于不同集合的方差.这说明训练后的高斯过程模型对同一集合的预测具有更大的可信度.在高斯过程建模时，根据训练集500组数据求取最优化参数.因此，它对训练集内1 000组数据预测时，准确度高于训练集外部的1 000组数据.由此可知：高斯过程模型对训练集外点预测的可信度已经降低，训练集内的预测效果高于训练集外的预测效果.

(a) 同一数集预测效果 (b) 不同数集预测效果图4 实际信号与预测信号对比图Fig.4 Actual signals and forecast comparison chart

(a) 同一集合误差曲线 (b) 不同集合误差曲线

(c) 同一集合方差曲线 (d) 不同集合方差曲线图5 预测的误差和方差曲线图Fig.5 Prediction error and variance of graph

3.3 基于小波的高斯过程模型预测结果

采用上面的500组作为训练样本，不同集合的1 000组作为测试样本.经过仿真结果比较可知：在误差分析和响应速度上，WT-GP模型预测的效果都有良好地改善.引入小波预测后，在误差分析上有变化.在训练和预测前,将信号进行小波三层分解，将小波分解得到的低频系数ca1和高频系数cd1，cd2，cd3分别训练和预测，分别重构得到低频分量和高频分量.各分量的实际值和预测值,如图6所示.

将得到的低频系数和高频系数组合重构，得到预测后的信号，如图7所示.由图7可知：预测信号和实际信号没有太大差别，而误差和方差的数量级依然很小.实验仿真用的数据不是同一集合，由此可见，其拟合能力和泛化能力依旧没变.比较图5与图7中非同一集合预测的误差，图7的误差更小一些，和图5中同一集合预测误差范围比较接近.

(a) 小波分解低频分量a3 (b) 预测低频分量a3

(c) 小波分解高频分量d1 (d) 预测高频分量d1

(e) 小波分解高频分量d2 (f) 预测高频分量d2

(g) 小波分解高频分量d3 (h) 预测高频分量d3图6 各分量的实际值和预测值Fig.6 Each component of actual value and predictive value

(a) 实际信号 (b) 误差曲线

(c) 预测信号 (d) 方差曲线图7 引入小波后的预测效果Fig.7 Prediction effect after introducing wavelet

两种预测模型运算时间的比较，如表1所示.表1中，运行时间指训练和测试所共用的时间.由表1可知：引入小波的高斯模型训练时间明显低于没有使用小波的情况.不论测试集合和训练集合是否来自同一集合，运行时间都会随着训练样本数的下降而明显变小；而当训练组数确定时，同一集合的时间略小于不同集合的运行时间.经过小波分解后的训练样本数减少，运行的时间有很大的变化.

表1 两种预测模型运算时间的比较

4 结束语

表面肌电信号是非线性的生物电信号，对其进行高斯过程回归建模预测，能很好地拟合其非线性.高斯过程建模时，首先,确定核函数；然后,训练高斯过程模型，从而得到最优超参数；最后,用训练好的模型进行预测.仿真结果证明，高斯过程对表面肌电信号有良好的拟合能力和强大的泛化性能.在此基础上，提出了基于小波的高斯建模，解决了单纯使用高斯过程建模带来的运行时间长和非同一集合预测误差大的缺点.从仿真结果来看，引入小波后的预测效果在减小误差和运算时间上都有明显的优势.

[1] 张启忠,席旭刚,罗志增.多重分形分析在肌电信号模式识别中的应用[J].传感技术学报,2013,26(2):282-288.

[2] RASMUSSEN C E,WILLIAMS C K I.Gaussian processes for machine learning (adaptive computation and machine learning)[M].American:MIT Press,2005:49-51.

[3] KOCIJAN J,GRANCHAROVA A.Application of gaussian processes to the modelling and control in process engineering[M]∥Studies in Computational Intelligence.Germany:Springer Berlin Heidelberg，2014:155-190.

[4] PARK C,HUANG Jianhua,DING Yu.Domain decomposition approach for fast gaussian process regression of large spatial data sets[J].Journal of Machine Learning Research,2011,12(4):1697-1728.

[5] HE Zhikun,LIU Guangbin,ZHAO Xijing,et al.Temperature model for FOG zero-bias using Gaussian process regression[J].Advances in Intelligent Systems and Computing,2012,180(1):37-45.

[6] 李鹏,宋申民,段广仁.改进的平方根UKF及其在交会对接中的应用[J].电机与控制学报,2010,14(11):100-104.

[7] 孙斌,姚海涛,刘婷.基于高斯过程回归的短期风速预测[J].中国电机工程学报,2012,32(29):104-109.

[8] WILLIAMS C K I,RASMUSSEN C E.Gaussian processes for regression[J].Advances in Neural Information Processing Systems Pages,1996,27(6):514-520.

[9] MURRAY-SMITH R,JOHANSEN T A,SHORTEN R.On transient dynamics, off-equilibrium behaviour and identification in blended multiple model structures[C]∥Proceedings of the European Control Conference.Karslruhe：IEEE Press，1999:BA-14.

[11] 张惠泽.基于高斯过程的pH中和过程控制研究[D].哈尔滨：哈尔滨工业大学,2010:26-29.

[12] 陈宝林.最优化理论与算法[M].北京：清华大学出版社,1989:280-288.

(责任编辑： 黄晓楠 英文审校： 吴逢铁)

Model Forecasting of EMG Using Wavelet Transformation and Gaussian Process

SHAO Hui, SU Fangyin, CHENG Haibo

(College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China)

According to the characteristics of the surface EMG signal, this paper uses wavelet transform and Gauss process modeling method to model and predict the surface EMG signal. The nonlinear surface EMG signal is used to model the fitting ability of the Gauss process, and the prediction effect is better, but the operation time is longer. To overcome the shortcomings of the long computation time, the wavelet decomposition of the surface EMG signal is processed, and the coefficients of the decomposition are modeled in Guassian. Experimental results show that the improved method has obvious effect on response time and prediction error.

surface electromyogram; Gaussian process; wavelet transform; model prediction

10.11830/ISSN.1000-5013.201606016

2016-01-14

邵辉(1973-)，女，副教授，博士，主要从事机器人控制、运动规划、智能控制、非线性系统LPV建模的研究.E-mail:shaohuihull@163.com.

福建省科技计划项目(2015H0026)； 教育部留学回国人员科研启动基金资助项目(Z1534004)； 福建省泉州市科技计划项目(2013Z34)

TP 391

A

1000-5013(2016)06-0743-06