飞行器操纵面嗡鸣的非结构网格并行计算方法

幺虹， 郭承鹏， 张颖

(中国航空工业空气动力研究院 高速高雷诺数气动力航空科技重点实验室， 辽宁 沈阳 110034)



飞行器操纵面嗡鸣的非结构网格并行计算方法

幺虹， 郭承鹏， 张颖

(中国航空工业空气动力研究院 高速高雷诺数气动力航空科技重点实验室， 辽宁 沈阳 110034)

为了数值模拟飞行器操纵面的嗡鸣现象，在集群计算机MPI并行计算环境下建立基于三维非定常欧拉方程耦合结构运动方程的嗡鸣计算方法.气动流场求解采用基于非结构网格的中心有限体积法进行空间离散，时间推进采用双时间方法，结构运动方程采用Adams预估校正方法求解.针对翼面与操纵面缝隙间存在的网格运动问题，在非结构网格系统上采用Delaunay图映射方法实现网格的运动变形.最后，使用飞行器操纵面标准嗡鸣计算模型对计算方法进行验证，结果表明:所建立的并行计算方法正确，程序具有很好的计算效率，能够对飞行器操纵面嗡鸣进行高效的数值分析.

嗡鸣； 飞行器； 操纵面； 并行计算； 动网格； Adams预估校正

飞行器操纵面嗡鸣是飞行器在跨音速飞行阶段发生的一种操纵面单自由度振动[1]，其本质特征与多模态耦合的经典弯/扭型颤振是完全不同的.Parker等[2]对美国航空航天局(NASA)的三维机翼操纵面标准模型(NASP)开展了嗡鸣响应特性的分析研究，发现操纵面上激波的运动和操纵面振动之间的相位差造成了嗡鸣现象.David[3]建立了操纵面偏转状态和铰链力矩之间的数学模型.Oddvar[4]使用Euler方程数值计算方法研究了跨音速副翼嗡鸣现象.刘千刚等[5]使用CFD手段开展了跨音速操纵面嗡鸣Hopf分叉分析及结构参数对嗡鸣特性影响的研究.史爱明等[6]基于Euler 方程，使用单自由度方法对机翼嗡鸣进行了数值模拟研究.张伟伟等[7]基于Euler 方程分析了二维翼型模型的B 型和C 型嗡鸣特性.杨国伟等[8]基于多块结构网格研究了飞机副翼嗡鸣现象.对于飞行器操纵面嗡鸣现象，激波及流动分离在其中起着非常重要的作用.由于非定常气动力和激波与操纵面相互干扰的特点，数值模拟计算量非常巨大，所以准确、高效的数值预测飞行器操纵面嗡鸣，对计算方法有较高的要求.本文研究在集群MPI并行计算环境下的飞行器操纵面嗡鸣计算方法和程序，采用MPI进行并行化处理以进一步提高计算效率，最后使用飞行器嗡鸣标准计算模型对计算方法和程序进行验证计算.

1 计算方法

1.1 非定常气动力计算方法

非定常气动力计算的控制方程采用三维可压缩非定常积分形式的欧拉方程，其守恒形式为

(1)

对方程(1)在空间方向上采用有限体积法进行离散，在时间方向上采用二阶精度的双时间方法进行离散，在伪时间上采用龙格-库塔方法进行推进.

1.2 操纵面结构运动方程求解

飞行器操纵面的运动可以用单自由度的结构运动方程描述[3]，忽略阻尼项，其具体形式为

(2)

1.3 非结构动网格方法

当前针对含运动边界的网格方法主要有网格变形方法、网格重构法[9]、浸入边界法[10-11]和嵌套网格法[12].除网格变形方法外，其他的动网格方法均要对流场进行插值，因而在非定常计算过程中会损失精度，文中采用不增加或减少网格节点并保持原网格拓扑结构的网格变形方法.近年来研究较多的径向基函数(RBF)动网格方法是Boer等[13]于2007年首次提出，也是一种需要全局信息的动网格方法，其计算精度高，但效率低.

考虑到翼面-操纵面缝隙间网格运动效率与鲁棒性要求，采用非结构网格进行计算，使用Delaunay方法实现网格的运动变形，具体有如下4个主要步骤.

步骤1 收集所有边界点，生成Delaunay背景网格图.

步骤2 建立计算网格节点和背景网格间的对应关系，计算插值权重系数.

步骤3 背景网格的运动和变形.

考虑到在整个计算过程中计算网格节点和背景网格单元之间的对应关系保持不变，即背景网格只需生成一次，同时为了便于实现网格变形模块的并行化，因此在程序设计上将前两步放到前处理程序进行处理；然后，将处理好的背景网格相关信息放到各个分区网格中，减少了实际并行计算过程中各线程之间的数据传递量.

(a) 运动前 (b) 运动后图1 非结构网格运动效果图Fig.1 Schematic motion effect of unstructured grids

使用文中开发出的基于Delaunay背景网格动网格方法对NACA0012翼型进行刚体旋转，动网格效果如图1所示.通过实际测试表明，使用基于Delaunay背景网格的动网格方法能够快速实现网格运动.

2 嗡鸣程序并行化设计

在中国航空工业空气动力研究院研发的非结构混合网格流场计算软件UNSMB的基础上进行嗡鸣程序设计.图2为嗡鸣程序的整体计算流程.在图2中，除了非定常流场并行求解以外，还需对操纵面的气动力矩、CSD计算模块和更新网格几何数据进行并行化处理.

图2 嗡鸣程序流程Fig.2 Flow chart of buzz program

操纵面气动力矩计算并行化设计的思路是，在每个物理时间开始之前(n-1时刻)，各进程分别计算本分区的操纵面气动力矩，使用MPI_Allgather将各区计算的气动力矩收集起来，在主进程中求和得到整个操纵面的气动力矩.在主进程进行结构运动方程的求解，可得到操纵面偏转角β，并输出该时刻的时间值及偏转角.然后，使用MPI_Bcast将偏转角β值发送到各个进程中，而各进程根据β值分别对该分区操纵面(仅操纵面物面表面网格)进行绕空间轴线旋转操作.使用MPI_Send和MPI_Recv将各进程上各分区的操纵面网格坐标收集到主进程当中，更新物面网格.

由物面网格、对称面网格、远场网格和足够大的一个背景网格区域，使用Delaunay方法生成背景网格.空间网格点就被Delaunay背景网格分区了，可以使用4个体积比表达的权值来表示空间网格点在Delaunay背景网格中的具体位置.物面边界更新之后，Delaunay背景网格各点的位置更新，空间网格随之更新.在此过程中，可以将Delaunay背景网格生成放到前处理部分.如此各分区更新操纵面表面网格之后，在本区就可以完成本区空间网格的更新，然后各进程分别对本分区的新网格点重新计算控制体几何信息、网格速度等.总体流程有如下6个主要步骤.

步骤1 前处理.使用Metis进行网格分区，Delaunay背景网格生成及网格点Delaunay背景图映射关系建立及权值的计算.

步骤2 气动力矩计算.每个物理时间步开始之前并行化计算气动力矩.

步骤3 结构运动方程求解.仅在主进程进行结构运动方程求解，然后将求解得到的操纵面偏转等信息发送到所有进程，并进行时间层的切换.

步骤4 网格运动.在各区上分别进行操纵面偏转操作，操纵面网格发生改变，然后使用Delaunay图映射法对空间网格进行运动.空间网格运动充分利用前处理分区信息及Delaunay图映射的映射关系不变的特点，方便进行并行化.

步骤5 处理网格几何信息.对更新后的网格计算法矢、面积、体积等几何信息，计算网格速度.

步骤6 进行下一时间步的流场计算.

嗡鸣计算程序并行化处理的关键是背景网格的处理,它充分利用了Delaunay图映射方法并行化程序设计方便、计算效率高的优点.经算例测试，该嗡鸣算例使用欧拉方程串行计算一个状态推进0.5 s(时间步长0.000 1 s)约需7 h，而采用并行计算，其总时间约4 h，并行效率基本呈线性关系.

3 NASP标模嗡鸣计算

3.1 计算模型及网格

NASP系列机翼是用于进行跨音速操纵面嗡鸣实验的一组不同平面形状的全翼展操纵面机翼[2,14].计算所采用的模型为NASA三维操纵面标准模型NASP，如图3所示.模型相关参数如下：操纵面质量m=0.267 624 kg，操纵面弦长c=0.101 6 m，转动频率f=16.5 Hz，转动惯量Iβ=88.17 Mg·m2，转动刚度Kβ=9.484 3 N·m·rad-1，其他几何参数详见文献[2].计算采用非结构纯四面体网格，整体计算域和计算网格示意图，如图4所示.图4中：网格节点数约8万个.

图3 NASP嗡鸣计算标准模型 图4 NASP模型表面及对称面计算网格Fig.3 NASP buzz computation standard mode Fig.4 Computation grids on surface and symmetrical plane for NASP model

(a) M=0.98，Q=1.532 2 kPa

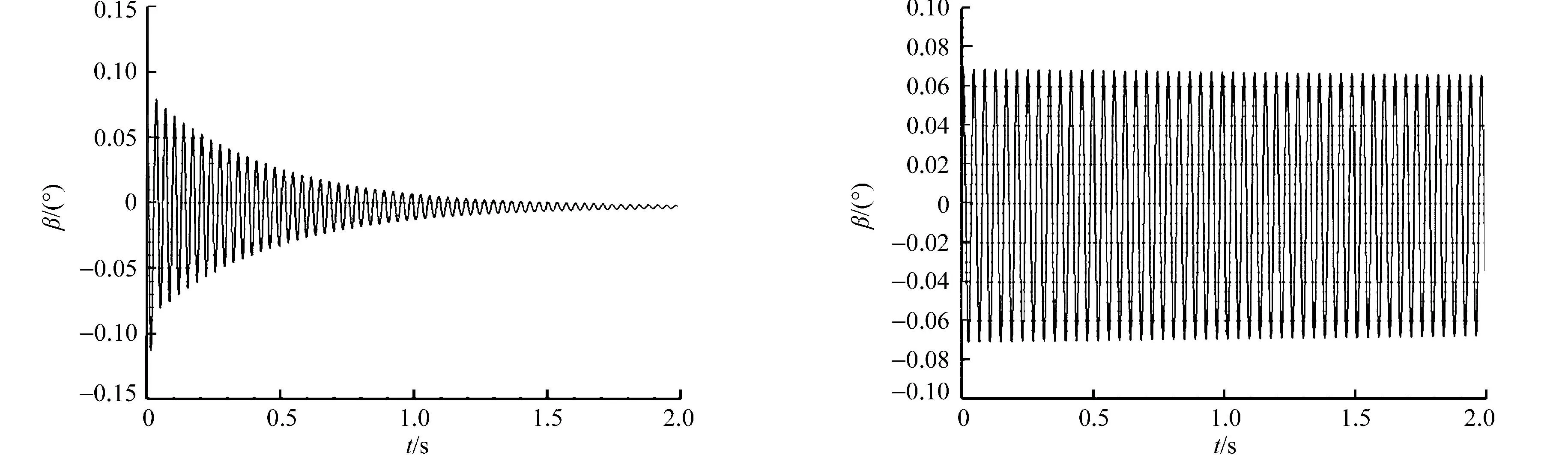
(b) M=0.96，Q=2.082 8 kPa (c) M=1.30，Q=1.819 4 kPa图5 不同风洞试验条件下操纵面偏角随时间的变化历程Fig.5 Change history deflection angle of control surface with time under experimental conditions of different wind tunnels

3.2 计算结果分析

对NASP标模M=0.98，Q=1.532 2 kPa工况的嗡鸣特性进行了计算.经过测试研究表明，非定常计算的内迭代步数和时间步长对计算结果(如嗡鸣的边界)有极大的影响.为此，选取时间步长为5×10-5s，内迭代步数为20步进行计算.共有80万个迭代，计算使用集群计算机环境，共使用CPU核心24个，机时4 h.在不同风洞试验条件下计算得到操纵面偏角随着时间的变化曲线，如图5所示.

从图5(a)可知：在0.5 s之前，操纵面偏角呈发散状态；到0.5 s之后，操纵面偏角在振幅9.3°做极限环振荡，计算结果与试验结果一致[2].假使操纵面转轴强度足够大，则操纵面在此状态下将以振幅9.3°做极限环振荡，振荡频率25.3 Hz，若结构强度不够，则在此状态，操纵面结构发生破坏.从图5(b),(c)可知：当把M值降低到0.96或提高到1.3时，操纵面偏角随时间变化呈收敛趋势.计算结果表明，在M<0.96或M>1.3时操纵面不会发生嗡鸣(等幅的极限环振荡)现象.

4 结束语

在中国航空工业空气动力研究院UNSMB软件的基础上，基于集群计算机MPI并行计算环境，研究了飞行器操纵面嗡鸣计算方法和程序模块，并对NASP操纵面嗡鸣标模进行了数值计算.结果表明，所提出的嗡鸣并行计算方法和程序模块能够高效、高精度地模拟操纵面嗡鸣现象，具有较高的工程应用价值.

[1] 叶正寅，张伟伟，史爱明.流固耦合力学基础及其应用[M].哈尔滨:哈尔滨工业大学出版社，2010:1-294.

[2] PARKER E， SPAN C，SOISTMANN D. Aileron buzz investigated on several generic NASP wing configurations[C]∥32nd Structures, Structural Dynamics, and Materials Conference.Baltimore:AIAA,1991.DOI:10.2514/6.1991-936.

[3] NIXON D.An analytic model for control surface buzz[C]∥36th AIAA Aerospace Sciences Meeting and Exhibit.Reno:AIAA,1998.DOI: 10.2514/6.1998-417.

[4] ODDVAR O B.Nonclassical aileron buzz in transonic flow[C]∥34th Structures, Structural Dynamics and Materials Conference.La Jolla:AIAA,1993.DOI: 10.2514/6.1993-1479.

[5] 刘千刚，代捷，白俊强.跨音速操纵面嗡鸣Hopf 分叉分析及结构参数对嗡鸣特性影响的研究[J].航空学报，1999，20(6):527-532.

[6] 史爱明，杨永年，叶正寅.跨音速单自由度非线性颤振: 嗡鸣的数值分析[J].西北工业大学学报，2004，22(4):525-528.

[7] 张伟伟，叶正寅，史爱明，等.基于Euler 方程的B 型和C 型嗡鸣特性数值研究[J].振动工程学报，2005，18(4):458-464.

[8] YANG Guowei，OBAYASHI S,NAKAMICHI J.Aileron buzz simulation using an implicit multiblock aeroelastic solver[J].Journal of Aircraft，2003，40(3):580-589.

[9] 周璇，李水乡，孙树立，等.非结构网格变形方法研究进展[J].力学进展，2011，41(5):547-561.

[10] SUDHAKAR Y，VENGADESAN S.Flight force production by flapping insect wings in inclined stroke plane kinematics[J].Computers & Fluids，2010，39(4):683-695.

[11] SHYY W，AONO H，CHIMAKURTHI S K.Recent progress in flapping wing aerodynamics and aeroelasticity[J].Progress in Aerospace Sciences，2010，46(7):284-327.

[12] HEATHCOTE J.Flexible flapping airfoil propulsion at zero freestream velocity [J].AIAA Journal，2004，42(11):2196-2204.

[13] BOER A，SCHOOT M S，FACULTY H B.Mesh deformation based on radial basis function interpolation[J].Computers and Structures，2007，85(11):784-795.

[14] SPAIN C，SOISTMANN D，PARKER E,et al.An overview of selected NASP aeroelastic studies at the NASA langley research center[C]∥2nd International Aerospace Planes Conference.Orlando:AIAA,1990.DOI:10.2514/6.1990-5218.

(责任编辑： 黄仲一 英文审校： 崔长彩)

Parallel Numerical Simulations of Aircraft Control Surface Buzz on Unstructured Grids

YAO Hong， GUO Chengpeng， ZHANG Ying

(AVIC Aerodynamics Research Institute， Aviation Key Laboratory of Science and Technology on Aerodynamics of High Speed and High Reynolds Number， Shenyang 110034， China)

In order to perform the numerical simulation of the buzz of aircraft control surface, a MPI parallel computation based on 3D unsteady Euler equations coupling with structural motion equations was established for cluster computers. In the solution process of pneumatic flow field, the spatial discretization was carried out using the centered finite volume method based on the unstructured grids. In addition, the time stepping was solved with the dual time method, and the structural motion equations were solved with the Adams predictor correction method. Aiming at the grid motion problem existing in the gap between the airfoil and control surface, the motion and deformation of grids were realized with Delaunay image mapping method in the unstructured grid system. Finally, the computation method was verified with the standard buzz computation model for the aircraft control surface. The results validated the established parallel computation method and indicated the excellent computation efficiency of the proposed model.

buzz； aircraft； control surface； parallel computation； dynamic mesh； Adams predictor-correction method

10.11830/ISSN.1000-5013.201606004

2016-10-10

幺虹(1963-)，女，高级工程师，主要从事飞行器非定常空气动力学的研究.E-mail:617162950@qq.com.

航空科学基金资助项目(2014ZA27003)

V 211.3

A

1000-5013(2016)06-0676-05