DFIG接入单机无穷大系统的阻尼转矩简化计算

杨玲玲，杜文娟，姚亦章，龚雁峰

(华北电力大学 电气与电子工程学院，北京 102206)



DFIG接入单机无穷大系统的阻尼转矩简化计算

杨玲玲，杜文娟，姚亦章，龚雁峰

(华北电力大学 电气与电子工程学院，北京 102206)

建立了双馈风力发电机各个部分的数学模型并简化，进而得出了双馈风机接入单机无穷大系统后的线性化模型。根据该线性化模型画出相应的Phillips-Heffron模型图。对于双馈风力发电机接入单机无穷大系统的情况，同步发电机的机电振荡回路受到的阻尼转矩来自两部分：一部分来自于同步发电机的励磁绕组及自动电压控制器(AVR)，另一部分来自于双馈风机。结合Phillips-Heffron模型图，得到同步机的励磁部分和双馈风机部分对机电振荡回路提供的阻尼转矩的完整算法。然后根据Phillips-Heffron模型图，对双馈风机部分提供的阻尼转矩进行简化分析，并提出两种简化方法。最后通过算例对所提阻尼转矩简化算法进行验证。结果表明，两种简化算法与完整算法结果相近，验证了简化的合理性。

双馈风机；单机无穷大系统；Phillips-Heffron模型；阻尼转矩分析法

0 引 言

近年来，风力发电已成为公认的“绿色电力”，在诸多新型能源开发与利用领域，风力发电技术最成熟且最具开发前景[1]。其中，交流励磁双馈型风电机组在实用化的风电技术中处于主流地位。随着并网风电规模的不断扩大，风能带给电网的小干扰稳定性问题备受关注，成为了新的研究方向[2-9]。

目前广泛使用的小干扰稳定性研究方法有两种：阻尼转矩分析方法(DTA)和模态分析方法(MA)[10-11]。基于经典控制理论的阻尼转矩分析方法是针对单机无穷大电力系统提出的，它简单易懂，物理意义清晰，从本质上分析了低频振荡的机理，能找到引起低频振荡弱阻尼的根本原因[12]。

文献[3]提出了广义元件的频率-功率动态特性的概念，依据所提的定义和命题，分析DFIG对电力系统阻尼的影响。文献[4]提供了一种分析DFIG风电场的接入对电力系统暂态和小干扰稳定的影响的研究方法。文献[5,6]则针对包含风电场的实际电网进行小干扰稳定分析。文献[13-15]研究了适用于小干扰稳定性分析的双馈感应风电机组的数学模型。文献[16]建立了双馈风机接入单机无穷大系统的详细线性化模型并进行了阻尼转矩分析。

本文建立了DFIG的简化三阶模型以及其接入单机无穷大系统后的线性化模型，并根据该线性化模型画出Phillips-Heffron模型图。与文献[16]不同的是，由于所采用的DFIG三阶简化模型不同，所得Phillips-Heffron模型图也不同。另外，本文着重对阻尼转矩法进行简化分析，进而在完整算法的基础上提出两种简化算法，并对其合理性进行了验证。

1 数学模型

1.1 双馈风机的简化数学模型

双馈感应发电机的定子直接接入电力系统，而转子侧依次通过机侧变流器、电容器、网侧变流器和变压器接入电力系统，如图1所示。

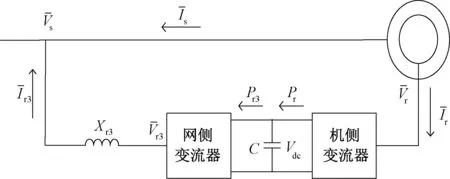
图1 DFIG接入电力系统示意图Fig.1 Schematic of DFIG connected to the power system

在DFIG完整模型的基础上，进行如下简化：

(1) 转子侧与电网连接处电感电流两阶动态描述的是电磁暂态过程，在研究机电暂态过程中可以将其忽略。基于此电磁暂态过程设计的网侧变流器的内环控制也随之忽略。

(2) 忽略电容电压的一阶动态方程。网侧变流器的外环直流电压控制环节也随之忽略。

(3) 双馈感应发电机的转子磁链两阶动态描述的是电磁暂态过程，在研究机电暂态过程中可以将其忽略。基于此电磁暂态过程设计的机侧变流器的内环控制也随之忽略。

(4) 由于DFIG的原动机部分并未参与到同步机的机电振荡环，因而在研究阻尼转矩时，可以将其忽略。

经过如上简化，机侧换流器的控制系统可以表示为图2。

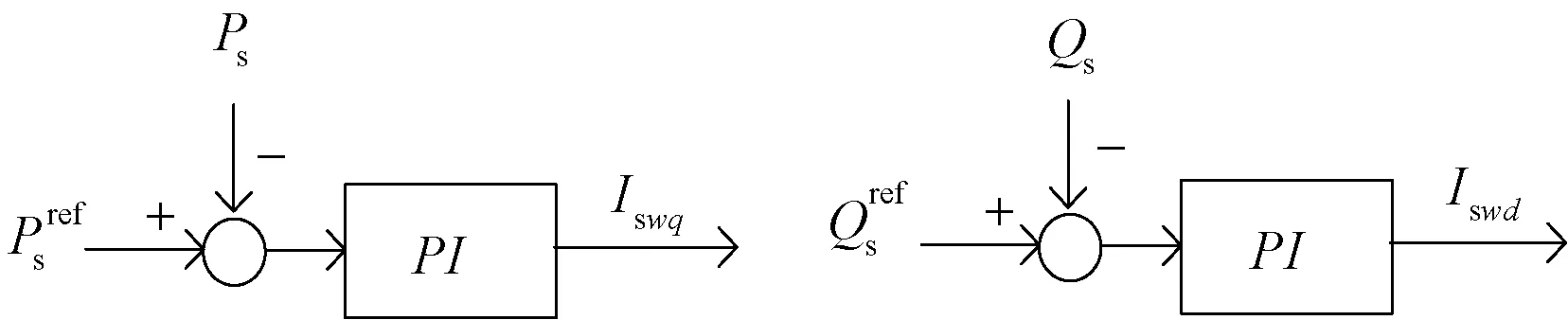
图2 机侧变流器的控制示意图Fig.2 Control schematic of machine side converter

由图2，采用定子电压定向，把双馈感应发电机旋转坐标轴的wq轴放在定子电压上，在wd-wq坐标系下，可得

其中，XP和XQ是两个PI控制器对应的状态变量，其微分方程为

双馈感应发电机的转子运动方程为

式中:Dw为转子运动阻尼系数;TJ为转子的惯性时间常数;sw0为稳态时的转差率。Twm为发电机输入的机械转矩，由机械部分参数确定，Twe为发电机的输出电磁转矩。

于是经过上面的简化，可得双馈风力发电机简化的三阶数学模型，包括转子转差率一阶和机侧换流器功率控制对应的两阶。

1.2 双馈风机接入单机无穷大系统的线性化模型

双馈风力发电机接入单机无穷大系统的结构图如图3所示。

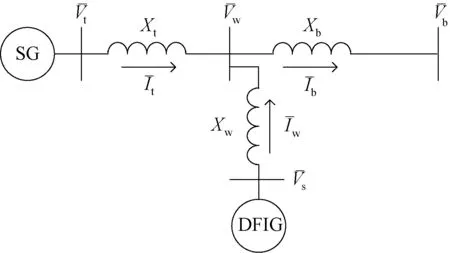
图3 DFIG接入单机无穷大系统的结构图Fig.3 Schematic of DFIG connected to single machine infinite bus power system

由于发电机电磁暂态过程很快，即使加了也不会影响秒级的机电暂态的仿真结果，故而同步发电机采用四阶动态方程：

经线性化，可以得到风电厂接入单机无穷大电力系统的线性化模型为

2 阻尼转矩分析

对于图3所示的双馈风力发电机接入单机无穷大系统的情况，同步发电机的机电振荡回路受到的阻尼转矩来自两部分：一部分来自于同步发电机的励磁绕组及自动电压控制器(AVR)，另一部分来自于双馈风机。前一部分表征了同步发电机的励磁部分对其转子运动方程的影响；后一部分则表征了双馈风机与同步发电机的动态交互影响，这种动态交互影响直接体现在在暂态过程中双馈风机与同步机之间的动态功率交换。

当计算只来自于同步机的励磁提供的阻尼转矩时，可以将双馈风机替代为恒功率源，这样就在保留双馈风机接入引起的潮流变化的同时，略去了双馈风机与同步机的动态交互对单机无穷大系统小干扰稳定性的影响，从而可以计算出同步机的励磁绕组及自动电压控制器对机电振荡回路提供的阻尼转矩。将双馈风机替代为恒功率源在数学上的表达为式(5)中的ΔP和ΔQ都设为0。

下面用四种阻尼转矩分析法分别计算上述两要素的分解计算。

2.1 完整算法

根据式(5)可得接入双馈风机后单机无穷大系统的Phillips-Heffron模型图，如图4所示。

对图4进行化简，得如图5所示的简化示意图。

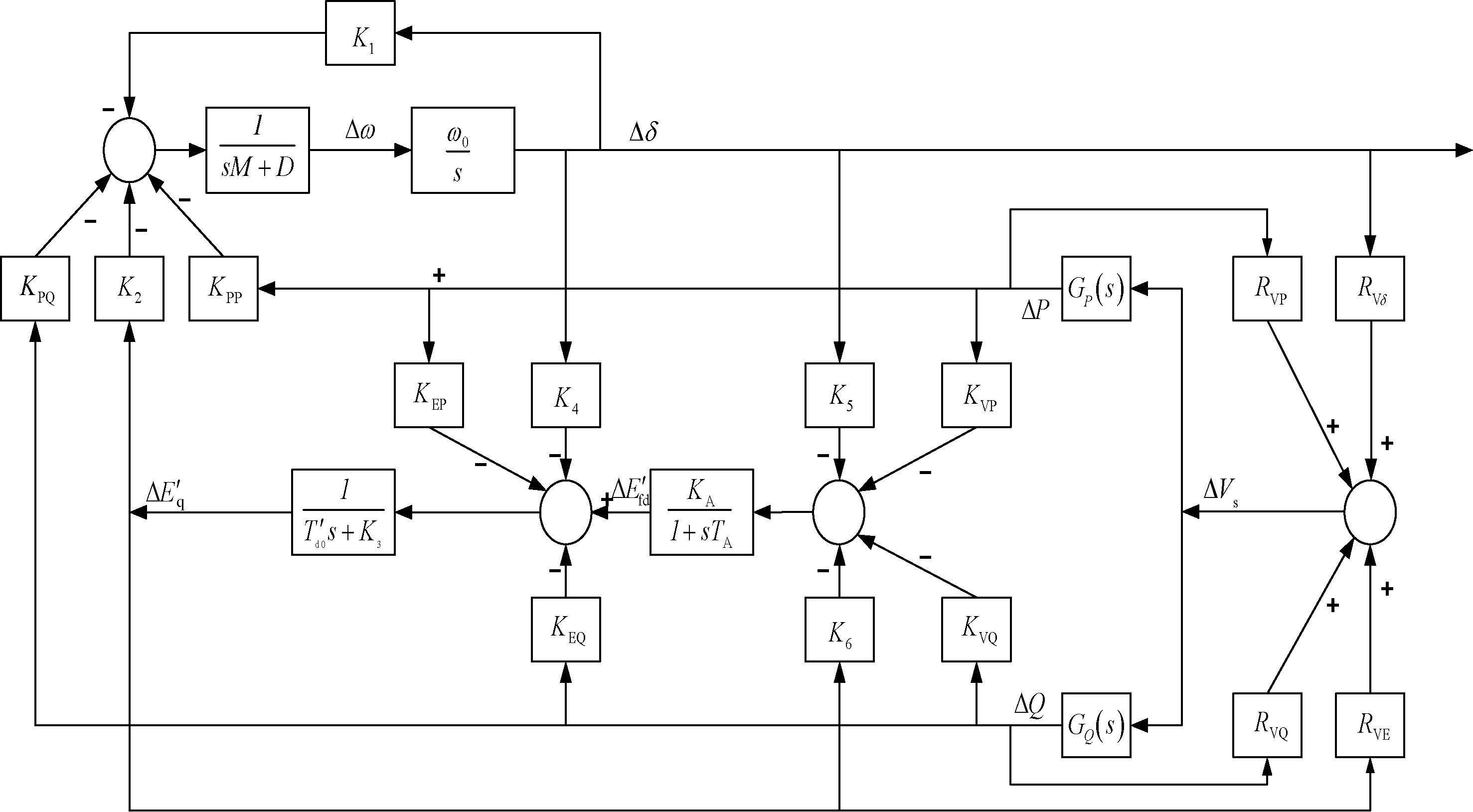
图4 图3所示系统的Phillips-Heffron模型图Fig.4 Phillips-Heffron model of system in Fig.3

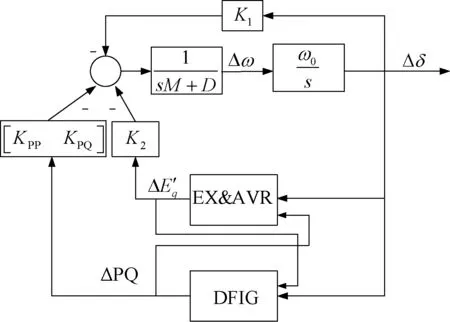
图5 图4所示的Phillips-Heffron模型简化图Fig.5 Simplified Phillips-Heffron model of Fig.4

由图5得

当忽略双馈风机的动态影响，即令ΔPQ=0时，由图5可得，同步发电机的励磁绕组及AVR部分提供的电磁转矩为

利用Δδ和Δω之间的关系式sΔδ=ω0Δω，可得

当振荡角频率为ωs时，由同步机的励磁部分提供的阻尼转矩系数为

当加入双馈风机的动态影响后，ΔPQ≠0，对机电振荡回路增加的电磁转矩来自于ΔPQ：

由式(6)的后两式可得

由式(8)和式(9)可得

2.2 简化算法一

图6清晰地给出了风力发电场和同步发电机之间的动态联系。可以看出风电场向同步机机电振荡回路提供的电磁转矩包括两部分：直接电气转矩 ΔTdet和间接电气转矩ΔTiet。根据阻尼转矩分析，电磁转矩又可以分解成同步转矩和阻尼转矩，风力发电厂提供的阻尼转矩决定了其对系统振荡稳定性的影响。一般情况下可以假设直接阻尼转矩要比间接阻尼转矩大得多，ΔTddt≫ΔTidt。这是因为信号经过路径a (path a) 和路径b (path b) 形成间接阻尼转矩，这两条路径中滞后环节一般情况下会削弱信号的强度。因此，在阻尼转矩分析中，可以只考虑直接阻尼转矩。

由图6可见：风力发电厂通过变量ΔEq′提供的阻尼转矩全部是间接的，这就意味着在阻尼转矩分析中若不考虑间接阻尼转矩就相当于忽略不计ΔEq′的影响。这样，在阻尼转矩分析中只考虑直接阻尼转矩部分，可以大大简化阻尼转矩分析的过程。

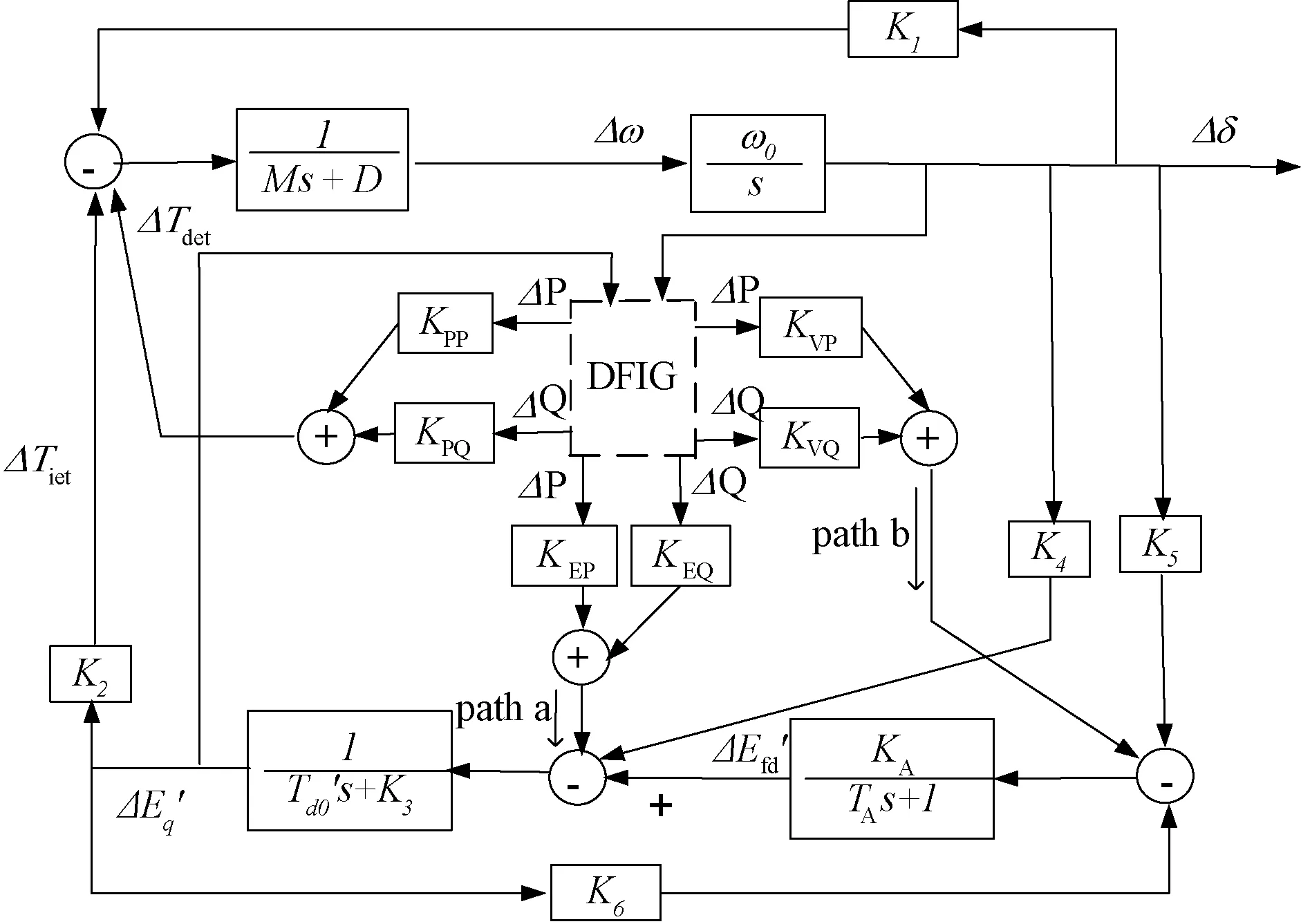
图6 有风力发电厂接入的单机无穷大系统线性化模型Fig.6 Linear model of single machine infinite bus power system with wind farm connected

图7所示为风力发电厂及其控制环节的线性化模型图。根据线性系统的叠加原理，图7中风力发电厂模型的两个中间变量(ΔP和ΔQ)向发电机机电振荡回路提供的阻尼转矩可以分别加以讨论。

如果只考虑ΔQ的影响，由线性叠加原理，可设RVP为零。由图6，中间变量ΔQ通过三个通道向发电机机电振荡回路提供阻尼转矩，其中，通道2 (path 2) 和通道3(path3)由于有一个滞后环节GP(s)及GQ(s)，信号被削弱。故风力发电厂中间变量ΔQ提供的直接阻尼转矩，应与其通过通道1 (path 1) 贡献的直接阻尼大致相当。故由图7，通过通道1提供的直接电磁转矩是

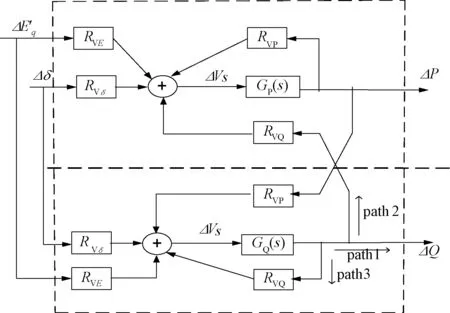
图7 风力发电厂及其控制环节的线性化模型Fig.7 Linear model of the wind power plant and its control part

同理，只考虑风力发电厂中间变量ΔP，可得所提供电磁转矩为

那么，风电场向同步机机电振荡环提供的电磁转矩为

在振荡角频率ωs下，风电场向机电振荡环提供的阻尼转矩为

2.3 简化算法二

在2.1节完整算法中，双馈风机通过G2部分向机电振荡回路提供的阻尼转矩为间接转矩，故而忽略G2，则风电场向机电振荡环提供的电磁转矩为

进而

3 算例分析

有DFIG接入的单机无穷大电力系统结构如图3所示。系统参数见附录。在MATLAB中编程仿真，得出DFIG和SG发出不同功率的各种工况下的仿真结果见表1～3及图8～10。

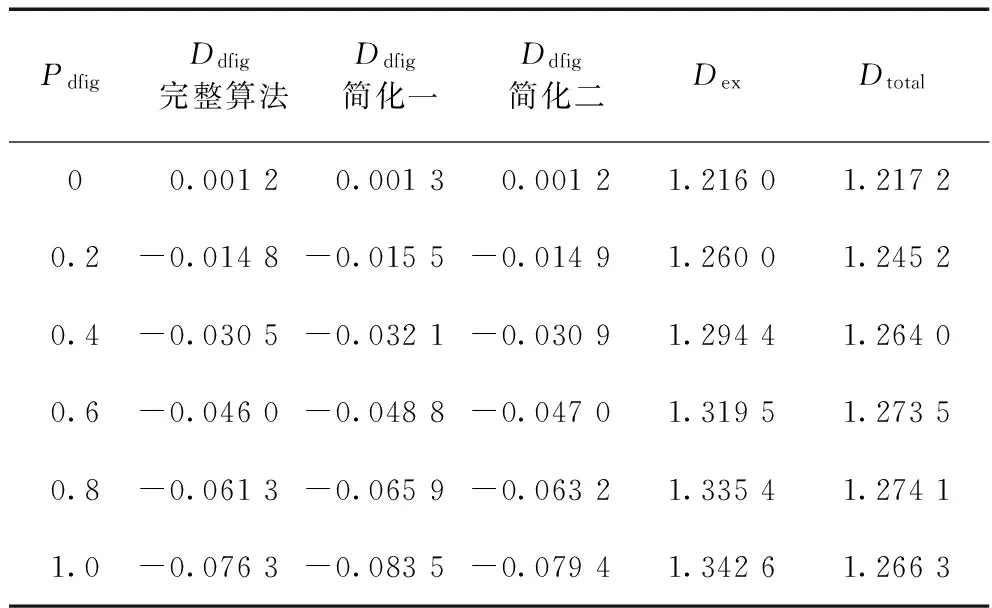
表1 SG功率为0.6，DFIG的功率变化时的结果

由表1及图8可以看出：(1)同步机励磁部分对机电振荡回路的阻尼转矩为正，说明励磁与同步发电机的动态交互有利于系统的小干扰稳定性。当同步机出力固定0.6时，随着DFIG发出功率的增加，励磁提供的阻尼转矩也会随之增加；(2)DFIG对机电振荡回路的阻尼转矩为负，说明DFIG与同步发电机的动态交互不利于系统的小干扰稳定性；随着DFIG发出功率的增加，DFIG提供的负的阻尼转矩也会随之增加。(3)励磁部分提供的阻尼转矩比DFIG所提供的阻尼转矩大的多，所以总的阻尼转矩为正。

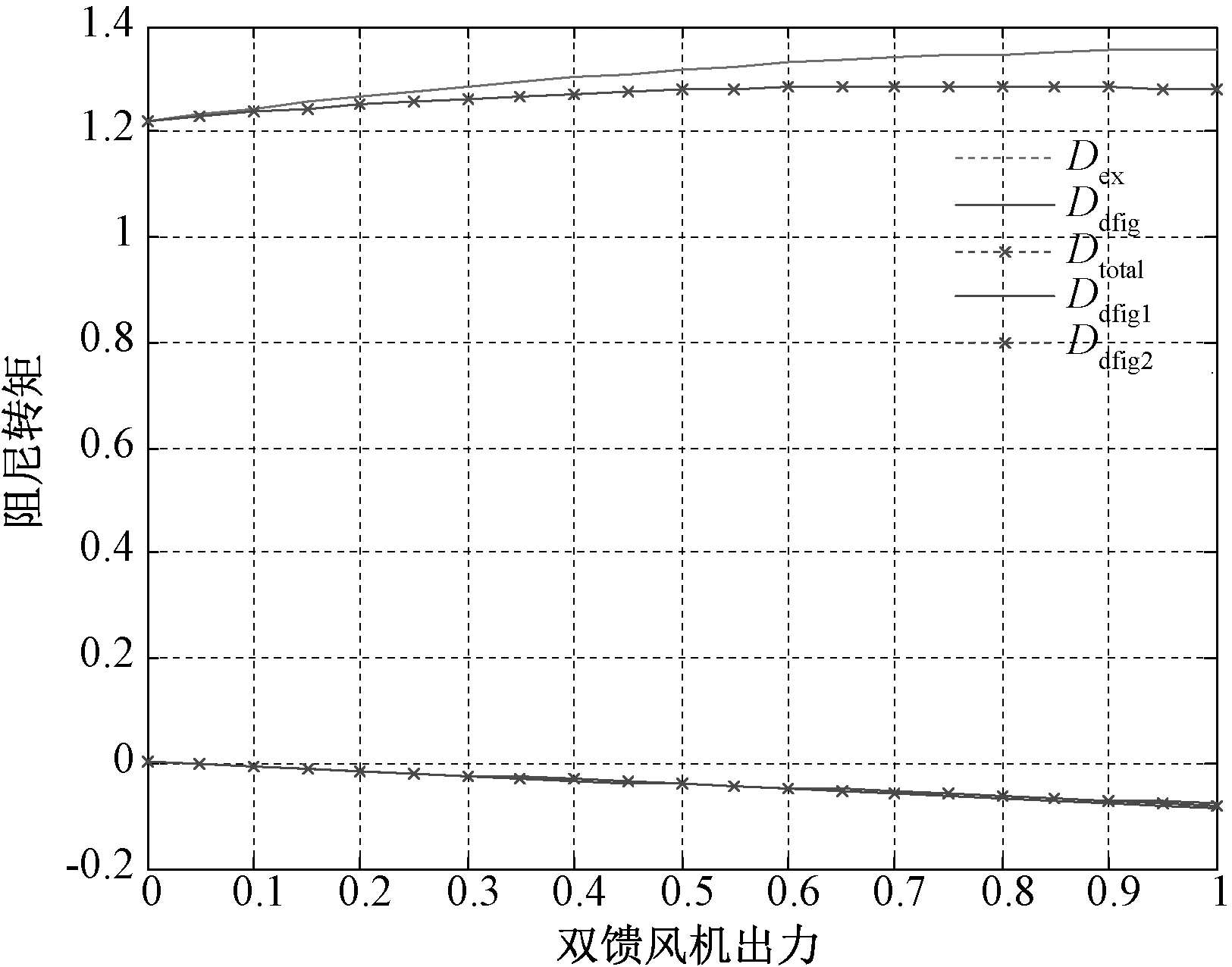
图8 SG功率为0.6，各阻尼转矩随DFIG功率变化图Fig.8 Damping torque figure with SG’s power fixed 0.6 and DFIG’s power changed

Tab.2 DFIG’s power fixed 0.6 and SG’s power changed

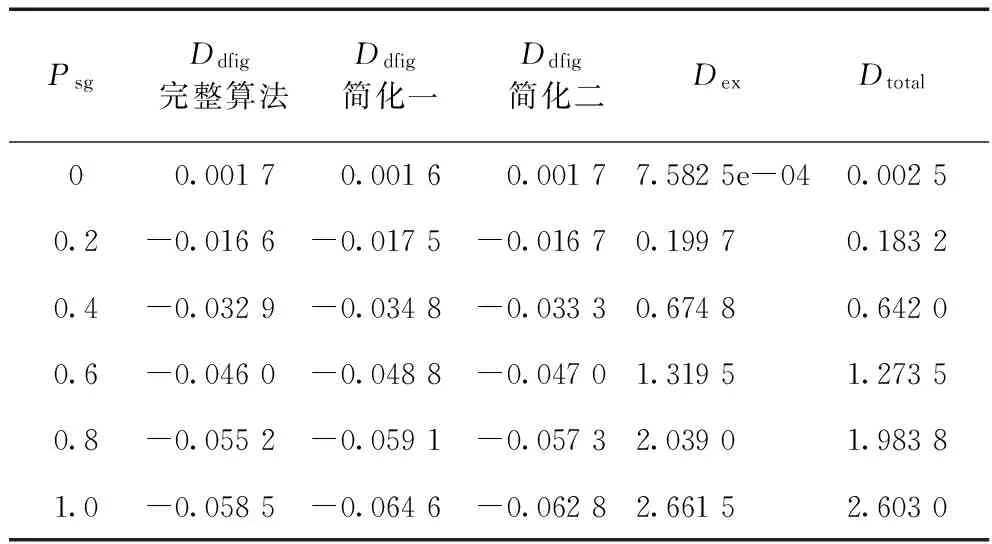
PsgDdfig完整算法Ddfig简化一Ddfig简化二DexDtotal00.00170.00160.00177.5825e-040.00250.2-0.0166-0.0175-0.01670.19970.18320.4-0.0329-0.0348-0.03330.67480.64200.6-0.0460-0.0488-0.04701.31951.27350.8-0.0552-0.0591-0.05732.03901.98381.0-0.0585-0.0646-0.06282.66152.6030

由表2及图9可以看出：(1)当DFIG出力不变，同步发电机的有功出力为0时，DFIG提供的阻尼转矩为正；当同步机的出力增大后，阻尼转矩值很快会由正变负，并随着同步机出力的增大，负的阻尼转矩会起来越大。(2)当DFIG出力不变时，随着同步机出力的增加，励磁提供的阻尼转矩一直为正，并且数值越来越大；(3)励磁部分和DFIG提供的总的阻尼转矩也是为正，并且有越来越大的趋势。

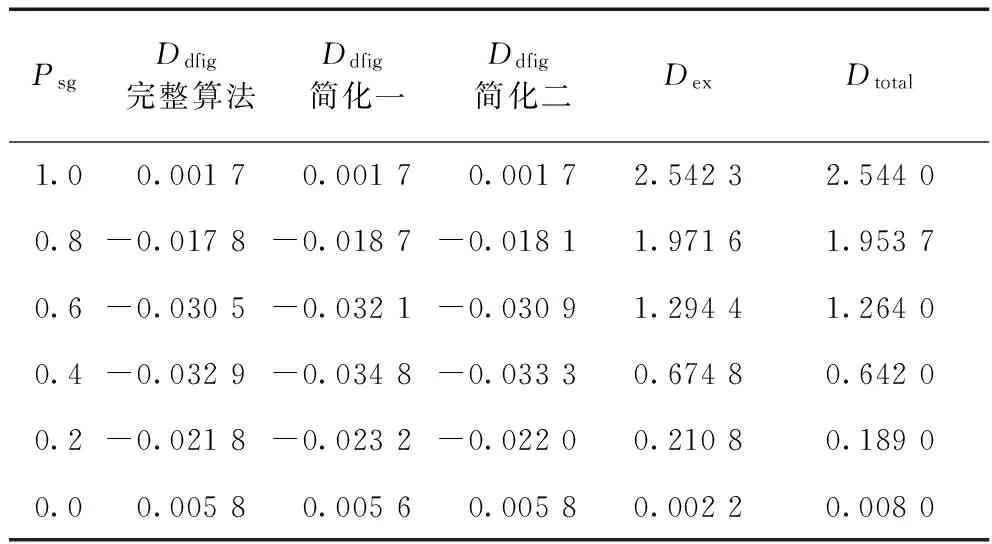
表3 DFIG和SG提供的总功率为1.0时的结果

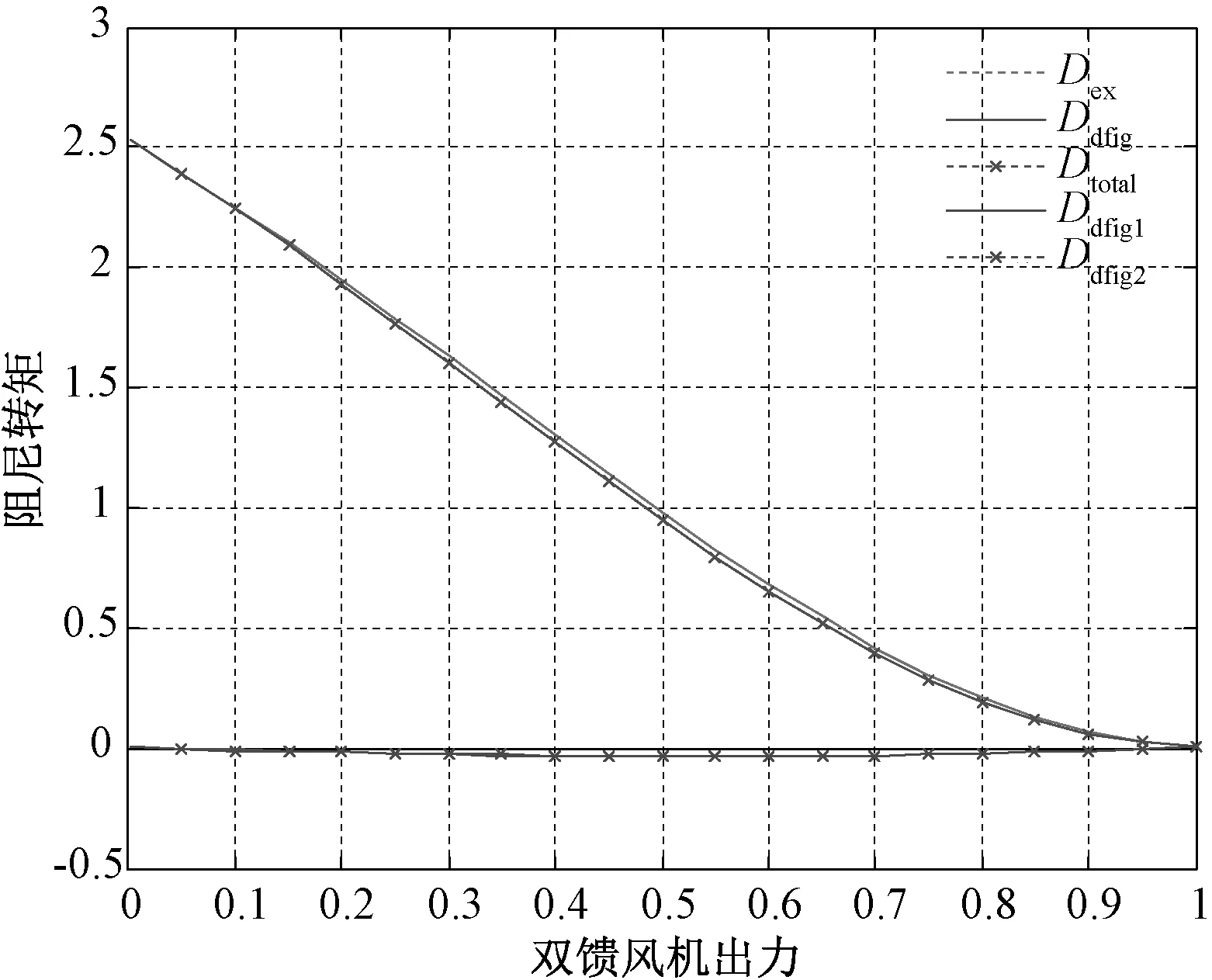
图10 DFIG和SG提供的总功率为1.0时阻尼转矩的仿真图Fig.10 Damping torque figure with total power of SG and DFIG fixed 1.0

由表3及图10可以看出：(1)当同步机和DFIG向无穷大母线提供的总功率保持不变时，随着同步机出力的增加，励磁提供的阻尼转矩一直为正，并且有越来越大的趋势；(2)随着DFIG出力的增加与同步机出力的减小，DFIG提供的阻尼转矩由接近为0的值先是减小，直到同步机和DFIG出力相同时到达最小值，之后DFIG提供的阻尼转矩会一直增大，最后增大到一个正值。(3)随着同步发电机出力的降低、DFIG出力的增加，总的阻尼转矩一直为正值，并且有越来越小的趋势。

综合表1～3及图8～10中不同工况下的仿真结果可看出，简化法一和简化法二计算结果都接近完整算法的结果，说明两种简化算法是合理的。其中，简化法二较简化法一更接近简化之前的结果。

4 结 论

(1)DFIG接入单机无穷大系统的不同工况下，励磁部分对机电振荡回路的阻尼转矩为正，说明励磁与同步发电机的动态交互有利于系统的小干扰稳定性。励磁提供的阻尼转矩大小会随着DFIG发出功率的变化而有所不同，但是比DFIG提供的阻尼转矩大得多，所以总的阻尼转矩为正。

(2)DFIG接入单机无穷大系统的大多工况下，DFIG对机电振荡回路的阻尼转矩为负，说明DFIG与同步发电机的动态交互不利于系统的小干扰稳定性。同时，不同工况下DFIG提供的阻尼转矩不同，有一定的变化规律，所以在实际系统中需要考虑SG与DFIG出力的大小配比，使DFIG提供的阻尼转矩尽可能大。

(3)阻尼转矩法分析有DFIG接入的单机无穷大系统时，可以采取较为准确的完整算法，也可以采取两种合理简化的方法。此种简化对于复杂电力系统的阻尼转矩计算具有一定的参考意义。

[1] 叶杭冶.风力发电机组的控制技术[M].北京：机械工业出版社，2002.

[2] 贺益康，胡家兵.双馈异步风力发电机并网运行中的几个热点问题[J].中国电机工程学报，2012，32(27)：1-15.

[3] 郝正航，余贻鑫.双馈风电场对电力系统阻尼影响的转矩分析[J].电工技术学报，2011，26(5)：152-158.

[4] GAUTAM D, VITTAL V, HARBOUR T. Impact of increased penetration of DFIG-based wind turbine generators on transient and small signal stability of power systems[J]. IEEE Transactions on Power System, 2009,24(3):1426-1434.

[5] 张红光，张粒子，陈树勇，等.大容量风电场对电力系统小干扰稳定和阻尼特性的影响[J].电网技术，2007，31(13)： 75-80.

[6] 杨涛，郑涛，迟永宁，等.大规模风电外送对电力系统小干扰稳定性影响[J].中国电力，2010，43(6)：20-25.

[7] TSOURAKIS G, NOMIKOS B M, VOURNAS C D.Effect of wind parks with doubly fed asynchronous generators on small-signal stability[J]. Electrc Power System Research, 2009,79(9):190-200.

[8] 李辉，陈宏文，杨超，等.含双馈风电场的电力系统低频振荡模态分析[J].中国电机工程学报，2013，33(28)：17-24.

[9] 杨黎晖，马西奎.双馈风电机组对电力系统低频振荡特性的影响[J].中国电机工程学报，2011，31(10)：19-24.

[10] WANG H F, SWIFT F J. The connection between modal analysis and electric torque analysis in studying the oscillation stability of multi-machine power systems[J]. Electrical Power & Energy Systems,1997,18(5):321-330.

[11] POURBEIK P, GIBBARD M J, VOWLES D J. Proof of the Equivalence of Residues and Induced Torque Coefficients for Use in the Calculation of Eigenvalue Shifts[J]. Power Engineering Review, 2002,22(1):58-60.[12] 杜文娟，王海风.电力系统低频功率振荡阻尼转矩分析理论与方法[M].北京：科学出版社，2015.

[13] 陈树勇，常晓鹏，孙华东，等.风电场接入对电力系统阻尼特性的影响[J].电网技术，2013，37(6)：1570-1577.

[14] WANG C, SHI L,WANG L,et al. Modelling analysis in power system small signal stability with grid-connected wind farms of dfig type[J]. Wind Engineering, 2008,32(3): 243-264.

[15] 魏巍，刘莹，丁理杰，等,改进的双馈风力发电系统小干扰模型[J].电网技术，2013，37(10)：2904-2911.

[16] LV C, DU W, LITTLER T. Damping torque analysis of power systems with DFIG wind turbine generators[C]//IET Conference Proceedings. The Institution of Engineering & Technology, 2015.

附录 算例参数

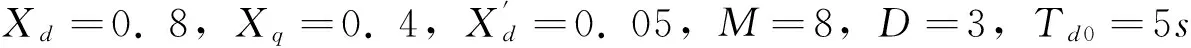
Simplified Calculation of Damping Torque of Single-machine Infinite-bus Power System Connected with DFIG

YANG Lingling, DU Wenjuan, YAO Yizhang, GONG Yanfeng

(School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China)

The mathematical model of each part of Doubly Fed Induction Generator (DFIG) is given and simplified, and the linear model of single-machine infinite-bus power system connected with DFIG is derived. According to the linear model, the figure of Phillips-Heffron model can be drawn. For single-machine infinite-bus power system with connected DFIG, the damping torque of electromechanical oscillating circuit of synchronous generator can be divided into two parts: one part is synchronous generator’s excitation winding and automatic voltage controller (AVR), the other part is DFIG. Integrity algorithm of the damping torque to the electromechanical oscillating circuit which is from excitation of synchronous generator and DFIG individually can be derived by using the figure of Phillips-Heffron model. Then, according to the figure of Phillips-Heffron model, the paper simplifies the damping torque from DFIG and proposes two simplified algorithms. Finally, DTA is validated by an example. Results of these two simplified methods are close to results of integrity algorithm, which verifies the rationality of simplification.

DFIG; single-machine infinite-bus power system; Phillips-Heffron model; Damping Torque Analysis (DTA)

10.3969/j.ISSN.1007-2691.2016.05.05

2016-01-04.

国家重点基础研究发展计划973计划资助项目(2012CB215204);自然科学基金资助项目(51407068);国家电网科技项目(SGZJ0000BGJS1500265).

TM614

A

1007-2691(2016)05-0029-07

杨玲玲(1992-)，女，硕士研究生，研究方向为电力系统分析、运行与控制；杜文娟(1979-)，女，副教授，研究方向为电力系统稳定性分析和运行控制；姚亦章(1991-)，女，硕士研究生，研究方向为电力系统分析、运行与控制；龚雁峰(1977-)，男，教授，博士生导师，研究方向为电力系统保护与控制、电力系统稳定分析等。