基于总效率最优的中低温余热有机朗肯循环性能
2016-12-07樊明强周天孙志强周孑民
樊明强,周天,孙志强,周孑民
(中南大学 能源科学与工程学院,湖南 长沙,410083)
基于总效率最优的中低温余热有机朗肯循环性能
樊明强,周天,孙志强,周孑民
(中南大学 能源科学与工程学院,湖南 长沙,410083)
为提高有机朗肯循环在回收中低温余热领域的效率,建立固定换热面积的蒸发器离散模型,分析变压力比、冷凝温度、蒸发温度和工质质量流率对有机朗肯循环性能的影响。研究结果表明:当蒸发温度和压力比一定时,存在不同的最佳冷凝温度使系统总效率和循环效率最高,其值分别可达8.95%和7.20%;当冷凝温度一定时,系统总效率随蒸发温度升高而增加;系统总效率与工质质量流率变化规律一致;而除在蒸发温度变化工况下,冷却水温度对系统总效率的影响不超过0.23%。
有机朗肯循环;中低温余热;离散模型
近年来,随着煤炭、石油、天然气等化石燃料的日益消耗,占总体余热近48%[1]且传统水蒸汽动力循环难以高效利用中低温余热回收[2],越来越受到人们的广泛关注。相比其他余热回收方法,有机朗肯循环凭借其简易、高效等优势已成为回收中低温余热的理想途径[3]。在有机朗肯循环中,循环工质往往决定着系统的性能。LIU等[4]研究发现水、氨、乙醇等湿流体工质由于其蒸发潜热较大,不适合用作有机朗肯循环工质。孙志强等[5−7]分析了工质类型对回收中低温余热有机朗肯循环性能的影响,发现在相同工况下,采用干流体工质的循环净功率和总热量回收效率比湿流体的大。GARY[8]发现当废热温度为150~200 ℃时,等熵流体R245fa的性能优于R123的性能。在有机朗肯循环应用系统分析和优化方面,WEI等[9−10]研究了烟气流量、进口温度、冷却空气流量及环境温度等对有机朗肯循环系统输出功率及循环效率的影响规律。BADR等[11−13]利用定泵和膨胀机效率的简单热动力模型比较了不同工质的系统循环效率,结果表明蒸发压力影响系统循环效率,且最优工质与具体适应工况相关。综上所述,国内外对有机朗肯循环的研究多集中在工质优选、系统参数对循环影响及优化方面[14−15]。对于工厂生产实际,希望尽可能减少换热器等装置的改造以达到最大回收余热的目的,因此,对已有换热装置的系统优化及最大系统总效率的研究有着极其重要的应用价值,而相关方面研究较少。本文作者旨在基本有机朗肯循环模型的基础上,研究在蒸发器换热面积一定下,以R245fa作为循环工质,探讨变压力比、冷凝温度、蒸发温度及工质质量流率对系统性能的影响。
1 有机朗肯循环系统及工质
1.1基本有机朗肯循环
基本有机朗肯循环系统简图如图1所示,图中t,P,M和N分别表示温度、压强、质量流率和转速。系统主要由蒸发器、膨胀机、冷凝器、储液罐和工质泵等组成,分为4个过程(1~4)。经冷却水冷却的有机工质通过工质泵输送到蒸发器中(过程1至过程2),与热源流体热交换成为饱和或过热蒸汽(过程2至过程3),推动膨胀机做功(过程3至过程4),排出的气体进入冷凝器,与冷却水热冷凝成为液体(过程4至过程1),再由工质泵输送到系统中,完成1个循环,从而实现能量的转换。
1.2工质的选取
有机朗肯循环采用有机流体作为工质。有机工质应具有良好的饱和气体曲线、较低的临界温度和压力、高汽化潜热,并且具有较强的热稳定性、不易燃、环境友好、价格便宜且易获得[16−17]。鉴于热源流体温度范围[18−19],选用R245fa作为循环工质。
R245fa为等熵流体且临界温度较高,不用考虑在膨胀做功过程中产生的液滴对膨胀机叶片造成的损害。其汽化潜热高达196.09 J/g,有助于提高热交换效率,且无腐蚀性,不可燃,因此,在实际运行中有较高的安全系数。其臭氧层破坏潜能值为0,属于环境友好型工质。
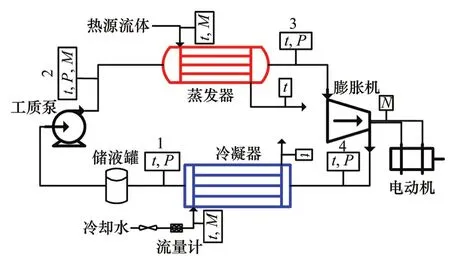
图1 有机朗肯循环系统图Fig. 1 Conceptual scheme of modeled ORC system
2 热力学分析
2.1蒸发器换热模型
采用单级蛇形管壳式换热器,工质在蒸发器中与热源流体逆流换热,从过冷液体状态变为饱和气体或过热气体状态。与此同时,热源流体温度从入口温度thf,i降低为出口温度thf,o,假定热源流体为理想气体,比定压热容cp为定值。
设蒸发器总换热面积为A,管道内径为d,管壁距壳壁距离为d。由于工质在换热器中存在相变,使对其整体分析变得复杂。为简化计算模型,忽略蛇形管弯折处影响,将其看成1个等同换热面积的水平直管道,同时按等换热面积离散成N段,如图2所示,认为每段工质流体物性参数一定[20],且能量和质量守恒,忽略动量和压降的影响。
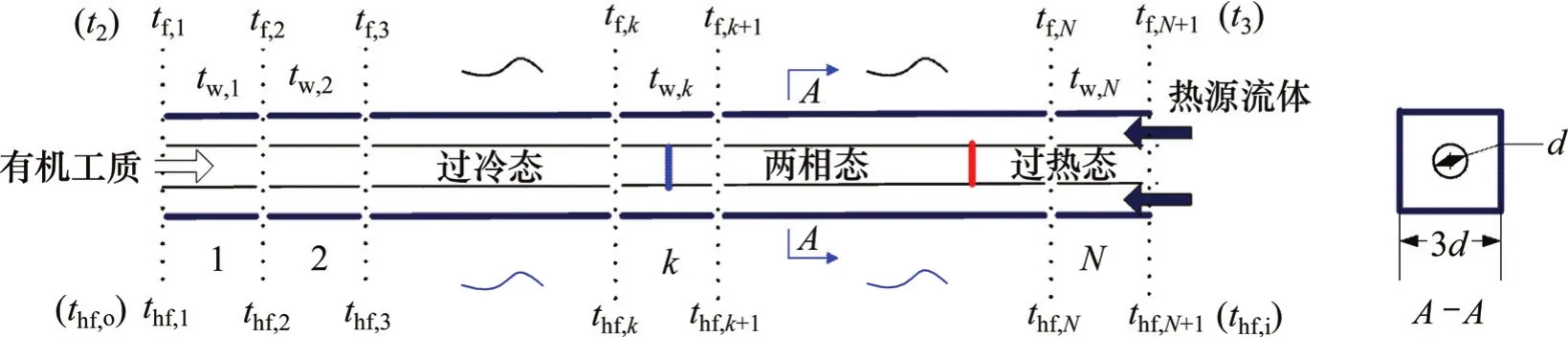
图2 蒸发器计算模拟图Fig. 2 Modeling paradigm of evaporator
对于任意k分段,蒸发压力、蒸发温度、换热面积、热源进、出口温度和工质进、出口温度分别定义为pev,tev,Ak(Ak=A/N,A为蒸发器换热面积,N为分段数),thf,k+1,thf,k,tf,k和tf,k+1(按照上述表示方法,图2中thf,N+1和thf,1分别与热源进口温度thf,i和出口温度thf,o表示同一温度;tf,1和tf,N+1分别为工质流体进口温度t2和出口温度t3表示同一温度),则由能量守恒可知

式中:mhf为热源流体质量流率;mf为有机工质质量流率;Hf,k和 Hf,k+1分别为工质流体k分段进出口比焓,其为压强pev、温度tf的函数,即Hf=f( pev,tf)。则有
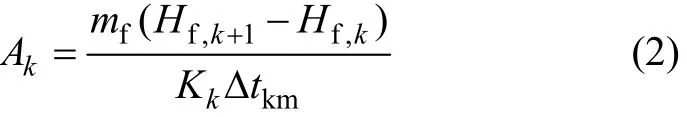
其中:

式中:Δtkm为对数平均温差;Kk为第k段总换热系数;Kf,k和Khf,k分别为工质和热源流体强制对流换热系数。
据式(2),将换热面积Ak与假定换热面积Ak0比较,在相对误差Z1之内则进入下一分段迭代,最终验算在总换热面积A一定时,thf,N+1与热源进口温度thf,i是否满足在相对误差Z2之内,若满足,则完成1次稳态运算,反之,改变相关参数重新运算。
迭代过程设置蒸发器中夹点温差Δtev[21]和工质出口过热度Δtf,out为:
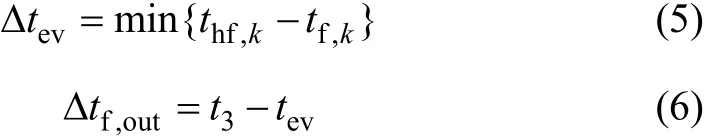
由此,可以得出工质出口温度t3下的比焓H3,则工质在蒸发器中吸热量Qevap为
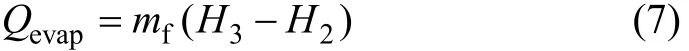
式中:H2为有机工质在蒸发器入口处比焓。
2.2冷凝器换热模型
有机工质在冷凝器中与冷却水逆流换热,从过热气体或饱和气体状态变为饱和液体状态,与此同时,冷却水吸收热量,从入口温度tw,i上升到出口温度tw,o。相比于蒸发器模型,冷凝器模型较为简单,令tc为冷凝温度,Δtc为冷凝器中传热的夹点温差。
根据能量守恒定律和冷凝器夹点温差Δtc可求冷凝器换热量Qc和水泵功耗Wwp,为:
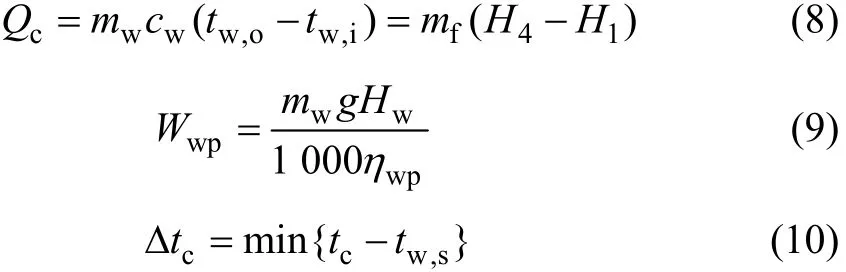
式中:mw为冷却水质量流率;cw为水比定压热容;H4和H1分别为冷凝器中有机工质进出口比焓;g为当地重力加速度;Hw为冷却水泵扬程;ηwp为冷却水泵等熵系数;tw,s为在有机工质饱和气相处冷却水温度。
2.3性能参数计算式
系统总净功率Woverall为膨胀机所作功减去工质泵、冷却水泵的功耗,即
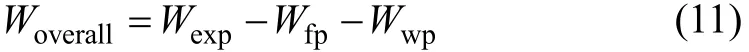
其中:Wfp为工质泵功耗。膨胀剂功耗Wexp为
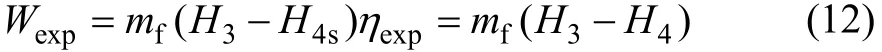
式中:H4s为理想情况下有机工质在膨胀机出口处比焓;ηexp为膨胀机等熵系数。
工质泵功耗Wfp为
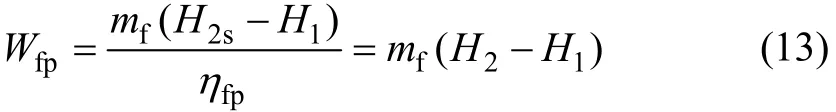
式中:H2s为理想情况下有机工质在泵出口处比焓;ηfp为工质泵等熵系数。
热源拥有最大热量Qhf为
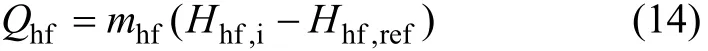
式中:Hhf,i为热源流体进口比焓;Hhf,ref为热源流体在温度t=20 ℃时(即环境温度)的比焓。
由式(7)和式(11)可知循环效率ηcycle为
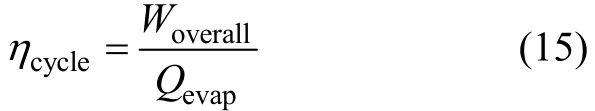
由式(7)和式(14)可知蒸发器效率ηevap为
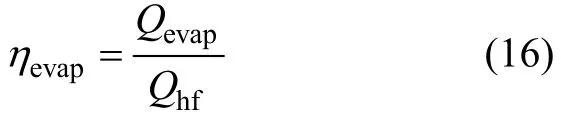
由式(11)、式(14)~(16)可知系统总效率ηoverall为
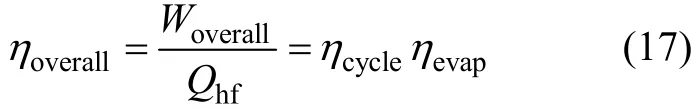
3 结果与分析
在进行结果分析时,本研究假定以下条件:1) 热源流体进口温度thf,i=200 ℃,质量流率mhf=0.1 kg/s,比定压热容cp=1 J/(g·K);2) 工质流体质量流率为mf=0.07 kg/s;3) 蒸发器换热面积A=3 m2,分段数N=100,相对误差Z1=0.001%,Z2=0.1%,所有管道直径d设为0.02 m;4) 膨胀机等熵系数为ηexp=75%,工质泵等熵系数为ηfp=72%;5) 冷却水泵扬程为Hw= 25 m,冷却水入口温度为tw,i=20 ℃,重力加速度g= 9.8 g/cm3,冷凝器夹点温度Δtc=5 ℃。
3.1变化蒸发温度下蒸发器夹点温度及过热度分析
由于本研究蒸发器换热面积给定,只要给予足够的换热面积,绝对温差可接近足够小。为避免出现热源流体与有机工质温差为0 ℃或负数的情形,设终止夹点温度。
在图3所示的不同蒸发温度(起始设置tev=85 ℃,每步增加5 ℃)、冷凝温度(起始设置tc=20 ℃,每步增加5 ℃)下,根据式(5)和式(6)计算,得到蒸发器中实际夹点温度Δtev和有机工质出口过热度Δtf,out变化规律,发现两者变化趋势基本相反。即实际夹点温度随蒸发温度的升高而升高,随冷凝温度的升高而降低;而工质出口过热度与之相反。由图3可知:夹点温度、出口过热度均为正值,可知蒸发器模型可满足本研究循环。
从整体蒸发器分析式来看,当冷凝温度一定时,随着蒸发温度的升高,过冷工质为达到饱和状态,需要吸收更多的热量,使过冷段换热面积增加,而蒸发器总换热面积一定,必将导致两相区和过热区换热面积的相对减少。对于工质而言,换热主要存在于两相区,这使蒸发器整体换热量Qevap减少,工质出口过热度降低,热源出口温度升高;当蒸发温度一定时,随着冷凝温度的升高,工质出口过热度变化不大,然而由于换热温差的存在,使热源出口温度相应增加,Qevap反而减小。
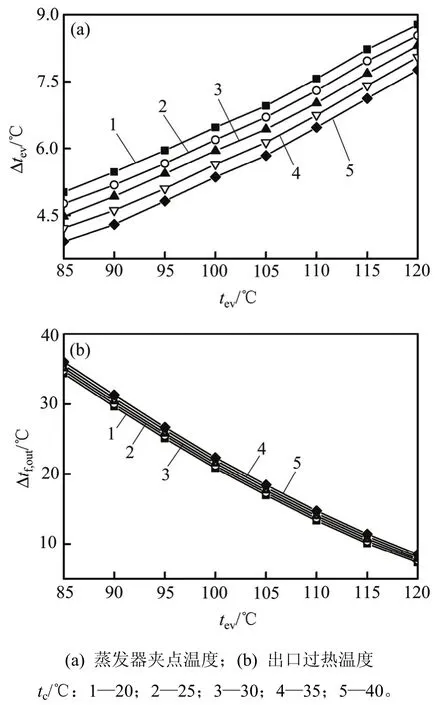
图3 不同冷凝温度下蒸发器夹点温度和出口过热度随蒸发温度的影响Fig. 3 Effect of evaporation temperature on Δtevand Δtf,outat various condensing temperatures
3.2固定压力比下有机朗肯循环性能分析
图4所示为在不同冷凝温度、压力比rp为2.5,3.0,3.5,4.0和4.5的条件下,根据性能参数计算式,得到的蒸发器效率ηevap、循环效率ηcycle和系统总效率ηoverall。由图4可知:当冷凝温度一定时,系统压力比rp越大,ηevap略微下降,而ηcycle和ηoverall越大。这是因为压力比的增大意味着蒸发温度的升高。由式(16)可知:当冷凝温度一定时,Qevap随蒸发温度的增大而减小,ηevap减少。而由式(8)~(10)可知:当冷凝器夹点温度一定时,冷却水温升一定,所需质量流率不变,从而水泵功耗Wwp不变,而膨胀机和工质泵进出口焓差随压力比增加而增加,即膨胀机做功Wexp和工质泵功耗Wfp增加,但由于工质泵进出口焓差较小,因此,由式(11)可知Woverall变化基本与Wexp变化类似,故ηcycle和ηoverall增加。当系统压力比一定时,随冷凝温度的升高,ηevap呈基本线性递减趋势,ηcycle和ηoverall均先增大后减少,同时存在最优冷凝温度,使此时循环效率和系统总效率最大。在压力比为2.5,3.0,3.5,4.0和4.5时,最大循环效率分别为6.05%,7.01%,7.78%,8.47%和8.95%,其所对应的冷凝温度分别为77,70,65,60和57 ℃;最大系统总效率分别为4.62%,5.47%,6.16%,6.77%和7.20%,其所对应的冷凝温度分别为41,40,38,37和37 ℃,因此,以有机朗肯循环最佳冷凝温度作为最佳系统冷凝温度,势必造成系统总效率(即系统实际对外输出功)减小。
由于在不同压力比下,膨胀机做功Wexp、工质泵功耗Wfp和水泵功耗Wwp变化趋势相似,故本文仅给出压力比为3.5情况下分析结果,如图5所示(图5中ηr为各功占热源拥有最大热量百分比)。从图5可见:Wexp和Wwp随冷凝温度的增加而降低,而Wfp与之相反;当冷凝温度低于38 ℃时,Wwp占有比例较大且下降幅度超过Wexp,而Wfp占有比例较小,由式(11)可知:系统总净功率Woverall呈上升趋势;当冷凝温度大于38 ℃时,Wwp可基本忽略不计,而Wfp占有比例增大,故Woverall呈下降趋势。由3.1节可知,冷凝温度升高,使蒸发器换热量Qevap相应减小。因此,通过式(15)和式(17)可知:Woverall增加,ηcycle增加;当Woverall的减小幅度小于Qevap时,ηcycle增加,反之,ηcycle减小。而ηoverall为Woverall与热源拥有最大热量Qhf之比。由于热源入口温度和质量流率及环境温度不变,由式(14)可得Qhf不变,故ηoverall的变化规律与Woverall的变化规律一致。故ηcycle和ηoverall对应的最优冷凝温度不同。
图6所示为冷却水温度对系统总效率ηoverall的影响。由图6可知:在不同冷却水温度下,随着冷凝温度升高,ηoverall均先增大后减小,存在不同最佳冷凝温度使ηoverall最大;当冷凝温度大于50 ℃时,ηoverall变化基本一致。这是因为冷却泵功耗相对其他部件可忽略不计,如图5所示。经计算表明,在冷却水温度为10,12,14,16,18和20 ℃时,最大ηoverall分别为6.39%,6.35%,6.30%,6.26%,6.21%和6.16%,最大差仅为0.23%,与之相对应的冷凝温度为29,32,32,35,36和38 ℃,存在一定的右移现象。因此,降低冷却水入口温度,对最优ηoverall的影响较小。为避免不必要的能量损耗,建议采用常温态冷却水即可。
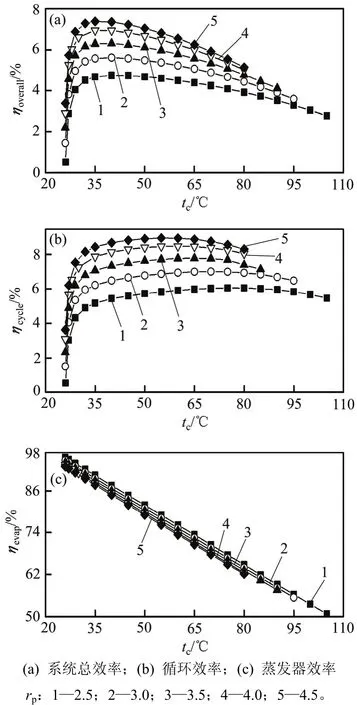
图4 不同压力比下ηevap,ηcycle和ηoverall随冷凝温度的影响Fig. 4 Effect of condensing temperature on ηevap, ηcycleand ηoverallat various pressure ratios
图5 压力比为3.5时功随冷凝温度的影响Fig. 5 Effect of condensing temperature on work with rpof 3.5
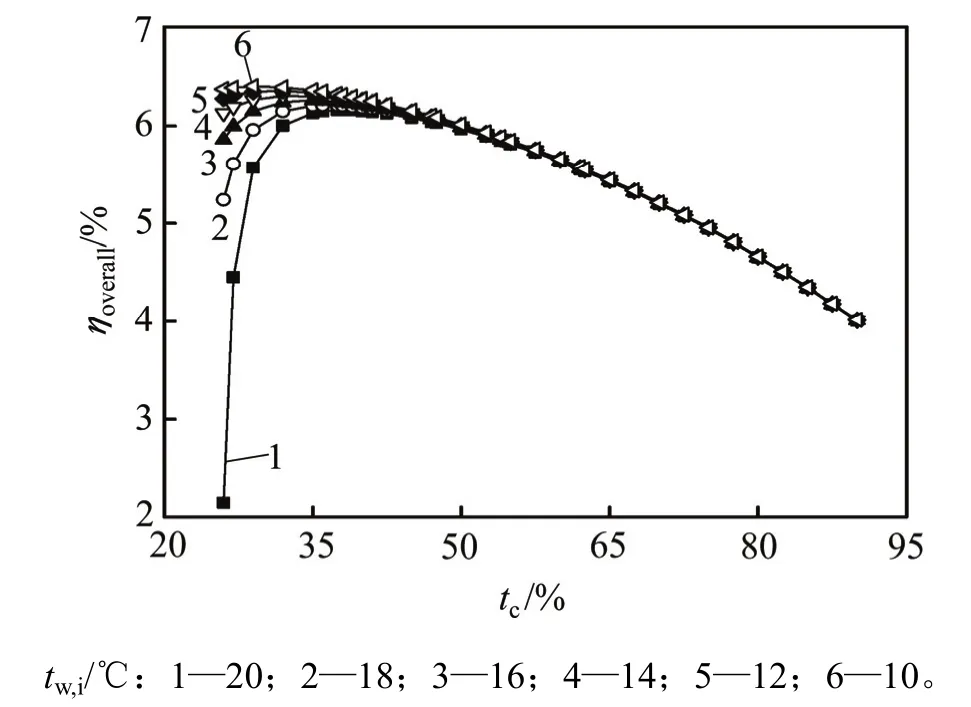
图6 压力比为3.5时系统总效率ηoverall在不同冷却水温度下随冷凝温度的影响Fig. 6 Effect of condensing temperature on ηoverallat various temperature of cooling water with rpof 3.5
3.3固定冷凝温度下有机朗肯循环性能分析
图7所示为蒸发温度、冷凝温度(tc=26,30,35,40和45 ℃)条件下,根据性能参数计算式,所得的蒸发器效率ηevap、循环效率ηcycle和系统总效率ηoverall。由图7可知:当蒸发温度一定时,在不同的冷凝温度下,除26 ℃外,各温度下ηcycle和ηoverall基本重合,且随冷凝温度的增加而轻微减少。这是因为水泵功耗的影响,由式(8)和式(10)可知:冷凝温度过低,使冷却水的温升降低,需要更大质量流率的水用于冷却工质,由式(9)得水泵功耗与冷却水的质量流率呈正比,故当冷凝温度为26 ℃时,水泵功耗占有比例较大,使ηcycle和ηoverall均较低;而当冷凝温度高出冷却水入口温度10 ℃后,水泵功耗基本可忽略不计,ηcycle和ηoverall主要受膨胀机作功影响。当冷凝温度一定时,随着蒸发温度的升高,ηevap逐渐减小,而ηcycle和ηoverall均呈增大的趋势,且变化曲线基本一致。
由于在不同冷凝温度下,膨胀机作功Wexp、工质泵功耗Wfp和水泵功耗Wwp变化趋势相似,故本文仅给出了冷凝温度为35 ℃情况下分析结果,如图8所示。由图8可知:Wexp和Wfp与蒸发温度的变化趋势相同,而Wwp基本保持不变。这是因为冷凝温度不变,故Wwp随蒸发温度的增加而基本不变,且占有比率极低,同时蒸发温度的升高,意味着系统压力比的增加,导致Wexp和Wfp增加。由于Wexp增加明显,由式(11)、式(16)和式(17)可知:系统总净功率Woverall呈增加趋势,并且蒸发器换热量Qevap的减少,使ηcycle逐渐增大,而热源拥有最大热量Qhf为常值,使ηoverall与Woverall变化规律一致,故ηoverall逐渐增大。
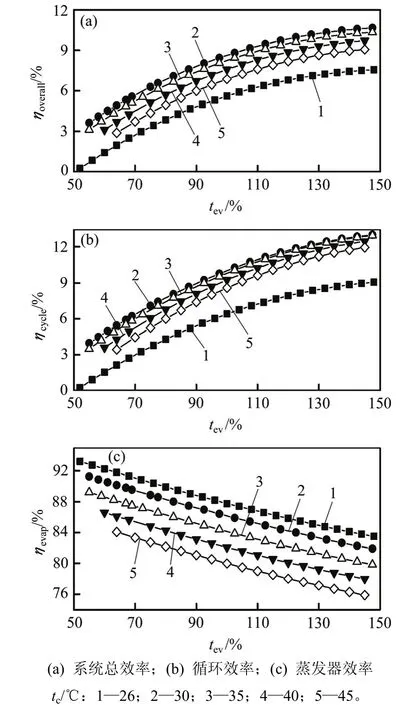
图7 不同冷凝温度下ηevap,ηcycle和ηoverall随蒸发温度的影响Fig. 7 Effect of evaporation temperature on ηevap, ηcycleandηoverallat various condensing temperatures

图8 冷凝温度为35 ℃时功随蒸发温度的影响Fig. 8 Effect of evaporation temperature on work with tcof 35 ℃
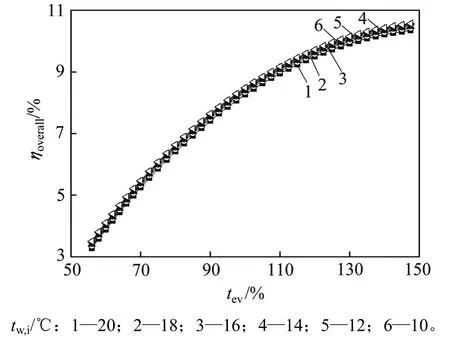
图9 冷凝温度为35 ℃时系统总效率ηoverall在不同冷却水温度下随蒸发温度的影响Fig. 9 Effect of evaporation temperature on ηoverallat various temperatures of cooling water with tcof 35 ℃
图9所示为冷却水温度对系统总效率ηoverall的影响。同样仅给出冷凝温度为35 ℃时分析结果:在不同冷却水温度下,随着蒸发温度的升高,ηoverall均逐渐增大,并趋于平缓。这是因为膨胀机作功占主要部分,如图8所示。在一定蒸发温度下,尽管ηoverall随冷却水温度的增加而减少,但变化不明显,曲线基本趋于重合。可见,只要冷凝水温差达到一定值时,其温度对系统影响较小,采用常温态冷却水即可满足循环要求。
3.4固定蒸发温度下有机朗肯循环性能分析
图10所示为冷凝温度、蒸发温度(tev=80,90,100,110,120和130 ℃)条件下,根据性能参数计算式,得到的蒸发器效率ηevap、循环效率ηcycle和系统总效率ηoverall。由图10可知:当冷凝温度一定时,ηevap与蒸发温度变化趋势相反,而ηcycle和ηoverall与之相同。由于随着蒸发温度的升高,蒸发器换热量Qevap减少,导致ηevap减少。同时,随系统压力比增加,由3.2节可知ηcycle和ηoverall随之增加。当蒸发温度一定时,ηevap呈基本线性下降趋势,而ηcycle和ηoverall均先增大后减少,同时存在最优冷凝温度,使此时的ηcycle和ηoverall最大。不同蒸发温度的最优ηcycle所对应的冷凝温度相同,均为31 ℃,此时最优ηcycle对应值分别为7.75%,8.98%,10.06%,10.98%,11.75%和12.36%,而最优ηoverall所对应的冷凝温度也相同,均为30 ℃,其值分别为6.84%,7.82%,8.64%,9.32%,9.85%和10.25%。
由于在不同蒸发温度下,膨胀机做功Wexp、工质泵功耗Wfp和水泵功耗Wwp变化趋势相似,故本文仅给出了蒸发温度为110 ℃情况下的分析结果,如图11所示。由图11可知:随着冷凝温度的升高,Wexp基本呈线性递减趋势,Wfp缓慢减少,可视为保持不变,这是由系统压力比减少所导致的;而当冷凝温度小于30 ℃时,由于冷却水的温升较小,通过式(9)可知,此时所消耗Wwp较大,反之,超过一定温度后其基本保持不变且比例较小。由式(11)可知,Woverall仅与Wexp和Wwp变化趋势有关,由于Wwp在冷凝温度小于30 ℃时减小幅度大于Wexp的减小幅度,故Woverall增加,反之则Woverall减小。这使ηcycle和ηoverall均先增大后减少,同时存在最优冷凝温度。由于冷凝温度的升高会造成Qevap轻微减少,而Qhf为常值,故最优ηcycle所对应冷凝温度相比最优ηoverall对应冷凝温度有一定增大,但相差较小。
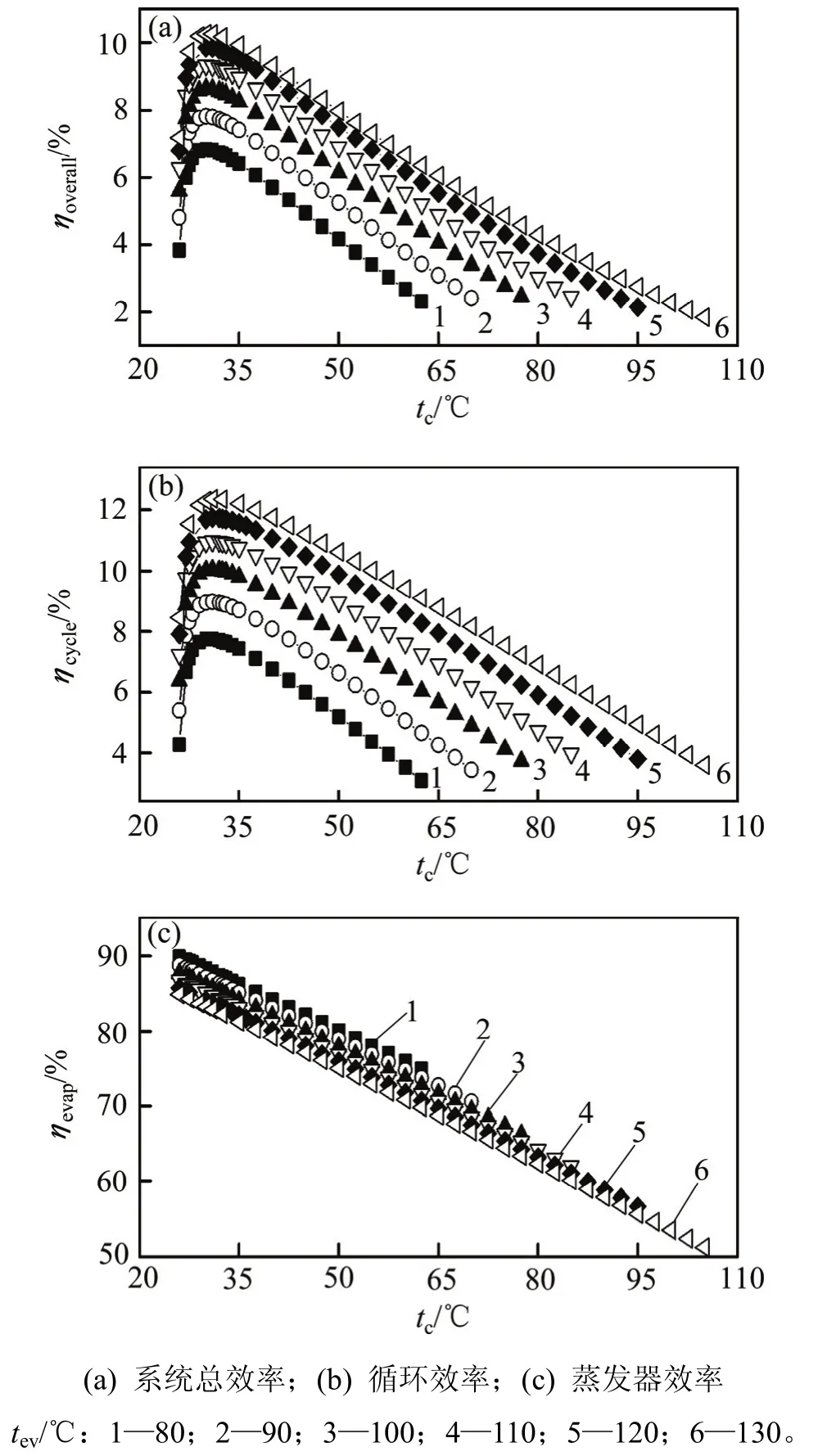
图10 不同蒸发温度下ηevap,ηcycle和ηoverall随冷凝温度的影响Fig. 10 Effect of condensing temperature on ηevap, ηcycleand ηoverallat various evaporation temperatures
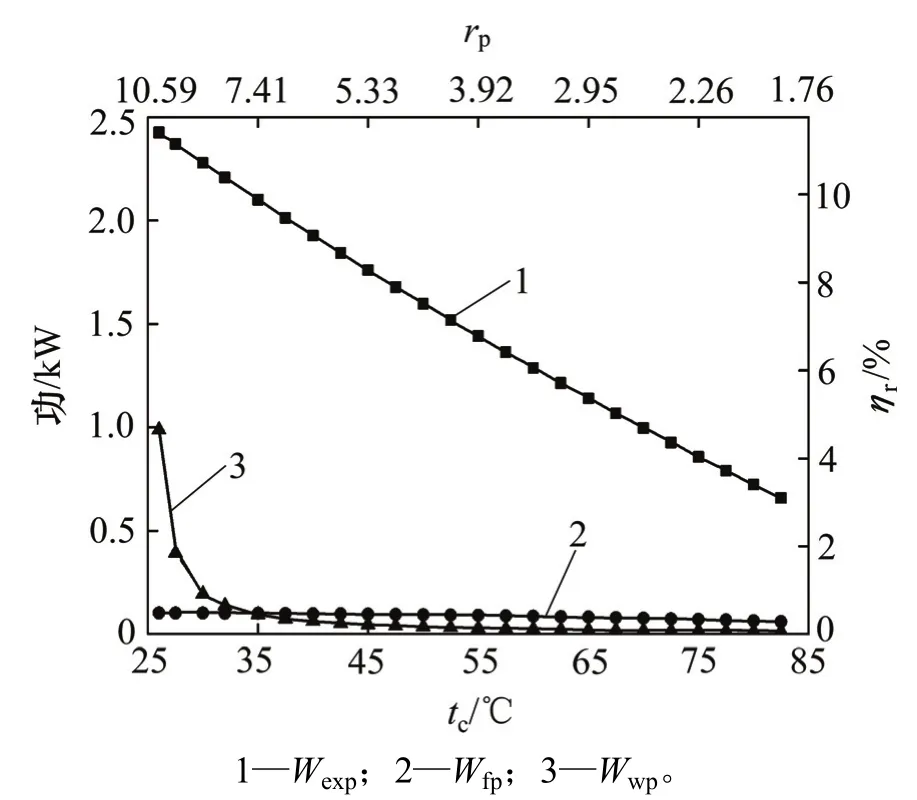
图11 蒸发温度110 ℃下功随冷凝温度的影响Fig. 11 Effect of condensing temperature on work with tevof 110 ℃
图12所示为冷却水温度对ηoverall的影响,同样仅给出蒸发温度为110 ℃时分析结果。由图12可知:在不同冷却水温度下,随着冷凝温度升高,ηoverall均先增大后减小,存在不同最佳冷凝温度使ηoverall最大。当冷凝温度大于40 ℃后,ηoverall变化基本一致,这是因为冷却泵功耗相对其他部件可忽略不计,如图11所示。在冷却水温度10,12,14,16,18及20 ℃时,最大ηoverall分别为11.02%,10.67%,10.32%,9.99%,9.65%和9.31%,最大差为1.71%,与之相对应的冷凝温度为20,22,24,26,28和30 ℃。故降低冷却水入口温度,对最优ηoverall的影响有一定影响。综合考虑成本及长期收益,选用较低温度冷却水如地下水,可提高系统总效率。
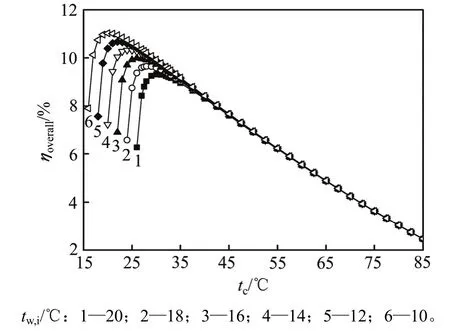
图12 蒸发温度为110 ℃下系统总效率在不同冷却水温度下随冷凝温度的影响Fig. 12 Effect of condensing temperature on ηoverallat various temperatures of cooling water with tevof 110 ℃
3.5变化工质质量流率下有机朗肯循环性能分析
在有机工质质量流率mf=0.07 kg/s情况下,通过更改有机工质质量流率,研究不同工质质量流率下系统性能参数的变化情况。在不同工况下,变化趋势相似,故这里仅给出不同工质质量流率(每步增加0.05 kg/s)、压力比(rp=2.5,3.0,3.5,4.0和4.5)情况下,系统总效率的变化趋势,如图13所示。
由图13可知:系统总效率ηoverall随压力比和工质质量流率的增加而增加。这是因为当蒸发温度和压力比一定时,增加工质质量流率,使工质密度增加,将导致蒸发器内单位换热面积换热量增加,从而蒸发器热源出口温度降低并且工质出口过热度也降低。由式(12)可知:尽管压力比一定,膨胀机进出口焓差变化较小,然而受工质质量流率的影响,导致实际膨胀机做功增加,由式(17)可知ηoverall增大。该结果与QUOILIN等[22]关于有机朗肯循环工质质量流率影响所得的结果一致。
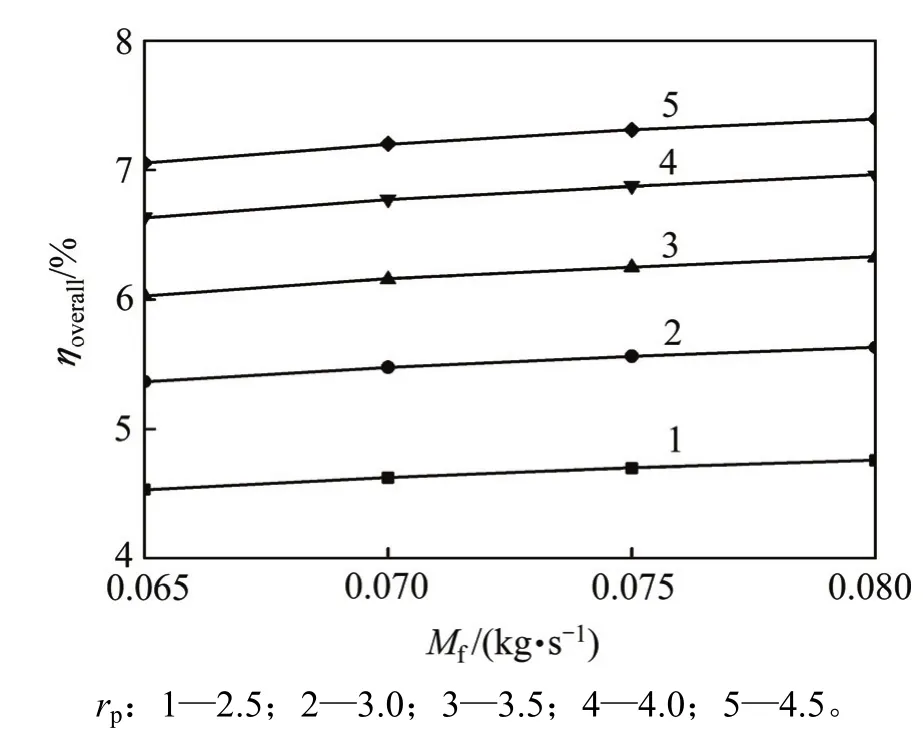
图13 在不同压力比下系统总效率随工质质量流率的影响Fig. 13 Effect of mass flow rate of refrigerant on ηoverallat various pressure ratios
4 结论
1) 在压力比和蒸发温度工况下,系统总效率和循环效率均先随着冷凝温度的升高而增大,当冷凝温度达到某一值后减小,且存在最佳冷凝温度使两者达到最大值,分别可达8.95%和7.20%,但其所对应的冷凝温度不同。因此,选用以循环效率对应最佳冷凝温度作为系统最佳冷凝温度,将造成实际净输出功减少。
2) 在冷凝温度工况下,系统总效率和循环效率均随着蒸发温度的增加而增加,因此,在考虑安全运行的条件下,提高蒸发温度,有助于提高系统输出功。
3) 系统总效率随工质质量流率单调变化,而不同冷却水温度对系统总效率的影响有限,除在蒸发温度工况下,其他工况下总效率变化不超过0.23%,因此,采用常温态冷却水冷却工质即可。
[1] 苑中显. 中国能源状况与发展对策[J]. 中国冶金, 2005, 15(5): 7−9. YUAN Zhongxian. The energy situation and development countermeasures in China[J]. China Metallurgy, 2005, 15(5): 7−9.
[2] 葛国耀. 美国工业节能及其启示[J]. 江苏科技信息, 2005(12): 10−13. GE Guoyao. The energy conservation and enlightenment in the industry of the United States[J]. Jiangsu Science and Technology Information, 2005(12): 10−13.
[3] GUO Tao, WANG Huaixin, ZHANG Shengjun. Comparative analysis of CO2-based transcritical Rankine cycle and HFC245fa-based subcritical organic Rankine cycle using lowtemperature geothermal source[J]. Science China: Technological Sciences, 2010, 53(6): 1638−1646.
[4] LIU B T, CHIEN K H, WANG C C. Effect of working fluids on organic Rankine cycle for waste heat recovery[J]. Energy, 2004, 29(8): 1207−1217.
[5] 孙志强, 易思阳, 郭美茹, 等. 利用中低温余热的回热有机朗肯循环性能分析[J]. 热能动力工程, 2015, 30(1): 24−30. SUN Zhiqiang, YI Siyang, GUO Meiru, et al. Performance analysis of an organic Rankine cycle for low-medium temperature waste heat recovery with heat regeneration[J]. Journal of Engineering for Thermal Energy and Power, 2015, 30(1): 24−30.
[6] 朱启的, 孙志强, 周孑民. 工质类型对回收中低温余热有机朗肯循环性能的影响[J]. 中南大学学报(自然科学版), 2013, 44(3): 1215−1220. ZHU Qidi, SUN Zhiqiang, ZHOU Jiemin. Effect of working fluid types on performance of organic Rankine cycle for low-and-medium temperature waste heat recovery[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 1215−1220.
[7] ZHU Qidi, SUN Zhiqiang, ZHOU Jiemin. Performance analysis of organic Rankine cycles using different working fluids[J]. Thermal Science, 2015, 19(1): 179−191.
[8] GARY J Z. Opportunities for HFC-245FA organic rankine cycle appended to distributed power generation systems[C]// Proceeding of the 21st International Congress of Refrigeration. Washington DC, USA: Island Press, 2003: 306−313.
[9] WEI Donghong, LU Xuesheng, LU Zhen, et al. Performance analysis and optimization of organic ranking cycle for waste heat recovery[J]. Energy Conversion & Management, 2007, 48(4): 1113−1119.
[10] 魏东红, 陆震, 鲁雪生. 废热源驱动的有机朗肯循环系统变工况性能分析[J]. 上海交通大学学报, 2006, 40(8): 1398−1402. WEI Donghong, LU Zhen, LU Xuesheng. Performances analysis of the organic Rankine cycle driven by exhaust under disturbance conditions[J]. Journal of Shanghai Jiaotong University, 2006, 40(8): 1398−1402.
[11] BADR O, OCALLAGHAN P W, PROBERT S D. Rankine-cycle systems for harnessing power from low-grade energy-sources[J]. Applied Energy, 1990, 36(4): 263−292.
[12] GU W, WENG Y, WANG Y, ZHENG B. Theoretical and experimental investigation of an organic Rankine cycle for a waste heat recovery system[J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2009, 223(3): 523−533.
[13] CHEN Y, LUNDQVIST P, JOHANSSON A, et al. A comparative study of the carbon dioxide transcritical power cycle compared with an organic Rankine cycle with R123 as working fluid in waste heat recovery[J]. Applied Thermal Engineering, 2006, 26(17/18): 2142−2147.
[14] VAJA I, GAMBAROTTA A. Internal combustion engine(ICE) bottoming with organic Rankine cycle(ORCS)[J]. Energy, 2010, 35(2): 1084−1093.
[15] PEI Gang, LI Jing, JI Jie. Analysis of low temperature solar thermal electric generation using regenerative organic Rankine cycle[J]. Applied Thermal Engineering, 2010, 30(8/9): 998−1004.
[16] BADR O. Selecting a working fluid for a Rankine cycle engine[J]. Applied Energy, 1985, 21(1): 1−42.
[17] MAIZZA V, MAIZZA A. Working fluids in non-steady flows for waste energy recovery systems[J]. Applied Thermal Engineering, 1996, 16(7): 579−590.
[18] ZYHOWSKI G J, BROWN A P, ACHAICHIA A. HFC-245fa working fluid in organic Rankine cycle-a safe and economic way to generate electricity from waste heat[C]// Proceedings of ECOS 2010. Lausanne, Switzerland: Elsevier, 2010: 231−239.
[19] 朱启的. 利用低温余热的有机朗肯循环性能分析及其工质优选[D]. 长沙: 中南大学能源科学与工程学院, 2013: 4−16. ZHU Qidi. Performance analysis and working fluid selection of organic Rankine cycle for low temperature waste heat recovery[D]. Changsha: Central South University. School of Energy Science and Engineering, 2013: 4−16.
[20] LIU Huawei, LI Saiwei, CHEN Yu. The melting of phase change material in a cylinder shell with hierarchical heat sink array[J]. Applied Thermal Engineering, 2014, 73(1): 975−983.
[21] GUO Meiru, ZHU Qidi, SUN Zhiqiang. Selection of organic rankine cycle working fluid based on unit-heat-exchange-area net power[J]. Journal of Central South University, 2015, 22(4): 1548−1553.
[22] QUOILIN S, AUMANN R, GRILL A. Dynamic modeling and optimal control strategy of waste heat recovery organic Rankine cycles[J]. Applied Energy, 2011, 88(6): 2183−2190.
(编辑 刘锦伟)
Performance of a low-medium temperature organic Rankine cycle(ORC) based on optimal overall energy conversion efficiency
FAN Mingqiang, ZHOU Tian, SUN Zhiqiang, ZHOU Jiemin
(School of Energy Science and Engineering, Central South University, Changsha 410083, China)
In order to improve the efficiency of organic Rankine cycle (ORC) in the field of low-medium temperature waste heat recovery, a discretized model of evaporator with constant heat exchange area was built. The effects of the pressure ratio, the condensing temperature, the evaporation temperature, and the mass flow rate of the refrigerant on the performances of the ORC were analyzed. The results show that the different optimal condensing temperatures are found to maximize the overall energy conversion efficiency and the cycle efficiency which can reach 8.95% and 7.20%, respectively, when both the evaporation temperature and pressure ratio are fixed. The overall energy conversion efficiency increases with the increase of the evaporation temperature at certain condensing temperature. The overall energy conversion efficiency is consistent with the mass flow rate of the refrigerant. The maximal influence of the temperature of cooling water on the overall energy conversion efficiency is less than 0.23%, except under the working conditions of varying the evaporation temperature.
organic Rankine cycle; low-medium temperature waste heat recovery; discretized model
TK11+5
A
1672−7207(2016)03−1030−09
10.11817/j.issn.1672-7207.2016.03.041
2015−04−11;
2015−06−20
国家自然科学基金资助项目(U0937604);长沙市科技计划项目(K1403055-11) (Project(U0937604) supported by the National Natural Science Foundation of China; Project(K1403055-11) supported by the Changsha Scientific Program)
孙志强,博士,教授,从事多相流测试技术、新能源与节能技术研究;E-mail: zqsun@csu.edu.cn
