基于滑模观测器的永磁直线同步电机速度控制

张 亮，许傲然，白 迪，谷彩连，王月志

(沈阳工程学院，沈阳110136 )



基于滑模观测器的永磁直线同步电机速度控制

张 亮，许傲然，白 迪，谷彩连，王月志

(沈阳工程学院，沈阳110136 )

针对永磁直线同步电机(PMLSM)在速度跟踪控制过程中因其模型具有非线性、参数时变性以及变量间的随机耦合等特点，导致电机速度跟踪控制精度低，提出了一种滑模观测器的永磁直线同步电机反馈线性化速度跟踪控制方法。首先建立了永磁直线同步电机的非线性模型，采用非线性坐标变换以及非线性状态反馈方法将电机系统进行了解耦处理，从而得到具有独立的非线性特点的电流和速度子系统。并设计了速度跟踪控制器，对反馈线性化所需要的动子加速度以及负载扰动信号,设计了一种扩张滑模观测器对其进行有效观测。仿真实验结果表明：该控制方法能够有效提高电机的速度跟踪精度拥有较好的鲁棒性。

永磁同步直线电机;速度跟踪控制;滑模观测器;稳定性

0 引 言

永磁直线同步电机(以下简称PMLSM)因其具有结构简单、体积小、功率密度高、转矩惯量大等优点，在数控机床、航天等领域得到了广泛应用[1]。在一些高精度领域中，要求永磁直线同步电机跟踪速度快、跟踪精度高，但PMLSM是一个非线性、多变量耦合系统，其控制性能在实际应用过程中往往受到机械参数的变化、外部负载扰动、内部参数变化和非线性动态特性等不确定性的影响[2]。在电机伺服系统中要求对电机速度进行精确跟踪并控制，但目前存在的问题是其模型具有非线性和变量间强耦合特点，给控制带来了很大难度。由于电流和速度的变化过程在时间尺度上非常接近，如果简单的采用磁场定向矢量控制方法进行静态解耦，电流和速度间的非线性耦合势必会破坏速度跟踪品质。为此能否实现变量之间的非线性的动态解耦，分别得到互不关联的线性速度模型以及电流模型，对于整个系统控制性能的提高至关重要。

为了提高电机的控制性能，获得良好的速度跟踪品质，近年来很多先进的控制方法在的PMLSM速度跟踪控制中得到了成功应用，例如自适应控制[3-4]、神经网络控制[5-7]、模糊控制[8-9]、滑模变结构控制[10]和反馈线性控制[11]等。其中反馈线性化思想的非线性控制理论得到了很大的发展，通过非线性坐标变换和非线性反馈将永磁同步电机的非线性系统转化为线性系统。文献[12]采用逆系统理论对该问题进行了研究，但该研究成果还仅仅停留在电流源型逆变器供电的电机上。文献[13]采用反推控制方法，该方法是一种较为新颖的非线性控制方法，以系统稳定性为基础，并逐步对控制器算法进行修正。文献[14]通过对输出变量进行李微分，以实现永磁同步电机系统输入和输出的线性化，但该方法也存在非线性扰动，将使系统误差性能变差等缺点。

本文在基于反馈线性化思想的非线性控制理论基础上，通过非线性坐标变换和非线性反馈实现PMLSM模型的线性化，将系统成功解耦成相互独立的线性的电流子系统和速度子系统。要实现电机速度的精确跟踪控制，就必须知道电机的动子加速度的精确信息。而采用加速度计成本过高，速度微分法又会引入噪声影响控制品质，为此本文设计了一种扩展滑模观测器以实现对电机动子速度和加速度的鲁棒观测，后对本文提出的控制策略进行了仿真验证。

1 PMLSM状态反馈线性化

通过Clarke变换和Park变换，在两相旋转坐标系下，永磁同步电动机的数学模型主要包括磁链方程、电压方程、转矩方程、运动方程和状态方程。其中磁链方程：

(1)

式中:φd,φq分别对应d轴和q轴的磁链；Ld,Lq分别对应d轴和q轴的电感。

电压方程：

(2)

式中:ud,uq分别对应d轴和q轴的电压；v为动子线速度。

电磁推力方程：

(3)

式中：p为极对数。

动子的状态方程：

(4)

式中:s为动子线位移；F1为负载的阻力；M为动子的总质量；B为粘滞摩擦系数。

设x=(id,iq,s,v)T,可以得到PMLSM的非线性数学模型：

(5)

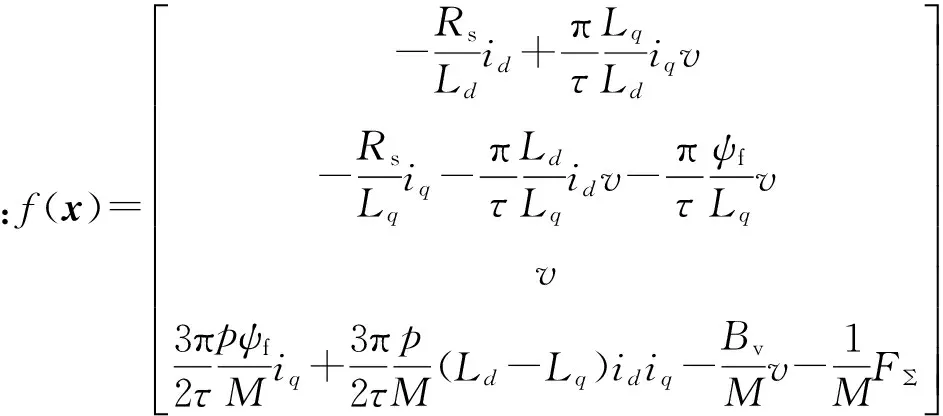
由式(5)可知，该系统中包含了速度和电流的非线性耦合项iqv，idv，idiq，为了减小因速度和电流之间的耦合对速度跟踪精度的影响，需要对非线性项进行解耦处理。

对式(4)求三次导数可得：

(6)

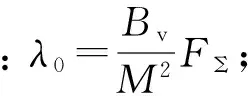
由式(3)和式(4)可得：

(8)

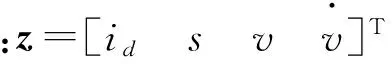
设非线性反馈控制律：

(9)

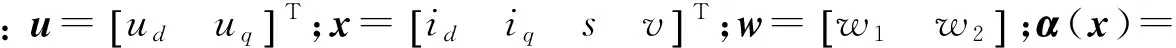
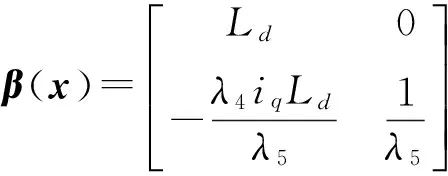
由式(8)和式(9)可以对式(5)反馈线性化解耦，由此可得：

2.审计委员会社会独立性研究。中国是一个重视人情的国家，费孝通教授（2007）指出中国特色的人情世故，使得企业内部的组织活动和外部的经营活动，都存在独特的社会关系。那么能否将这种特色的社会关系引入审计委员会？这种社会关系又会怎样影响审计委员会成员的独立性？为此，我们进一步梳理有关社会关系的文献。

(10)

由上式可知，式(5)被解耦成两个相互独立的线性系统。

2 速度控制器设计

设计解耦后的式(10)的速度跟踪控制律：

(11)

式中：idref为直轴参考电流;vref为动子速度参考轨线。

式(11)可以等效：

(12)

由式(11)可以得到误差动态方程：

(13)

由此可以看出对增益kid，kI，kP以及kD进行适当调整便可使系统误差达到稳定点ε=0。

3 滑模观测器的设计

为了估计系统状态和观测扰动能够同时进行，设计了一种扩展滑模观测器。通过对扰动的观测和反馈可以有效抑制扰动，进而保证系统闭环渐进的稳定性。

对式(10)做如下扩展可得到扩展系统：

(14)

由式(14)进行滑模观测器设计，滑模观测器设计：

(15)

由式(14)和式(15)可得估计误差动态方程：

(16)

图1 滑模观测器结构原理图

由式(9)、式(11)和式(15)可得基于滑模扩展观测器的控制策略：

(17)

(18)

由式(5)、式(7)和式(11)、式(17)可得整个系统的闭环方程：

(19)

跟踪误差动态方程：

(20)

通过扩张滑模观测器以及反馈控制器得到的闭环系统误差状态方程：

(21)

基于滑模观测器的永磁同步电机速度跟踪原理如图2所示。

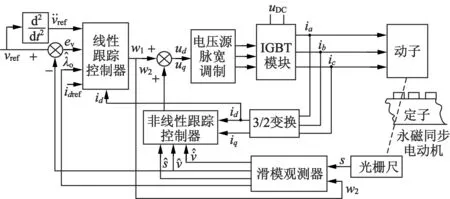
图2 滑模观测器的永磁同步电动机速度跟踪原理

4 仿真分析

为了验证上述方法的可行性，基于MATLAB软件，对采用传统矢量控制方法和基于扩展滑模观测器的控制方法的永磁同步电机速度跟踪控制进行了仿真。选取线性跟踪控制器的增益为kid=30，kP=251，kI=24.6，kD=0.34。选择滑模观测器的增益系数ks=120，kv=6 000，ka=1.24×104，kλ=106。永磁直线同步电机参数为：Rs=1.2 Ω，Ld=Lq=L=18.0 mH，τ=30 mm，Mn=11 kg，Bn=1.2 N·s/m，Φf=0.001 44 Wb，p=3，Fen=100 N，idref=0。

当系统起动和突然负载时，采用这两种控制方式时对比曲线如图3所示。图3(a)、图3(b)为系统起动时转速对比曲线；图3(c)、图3(d)图6分别为当负载突然减小到0时转速。

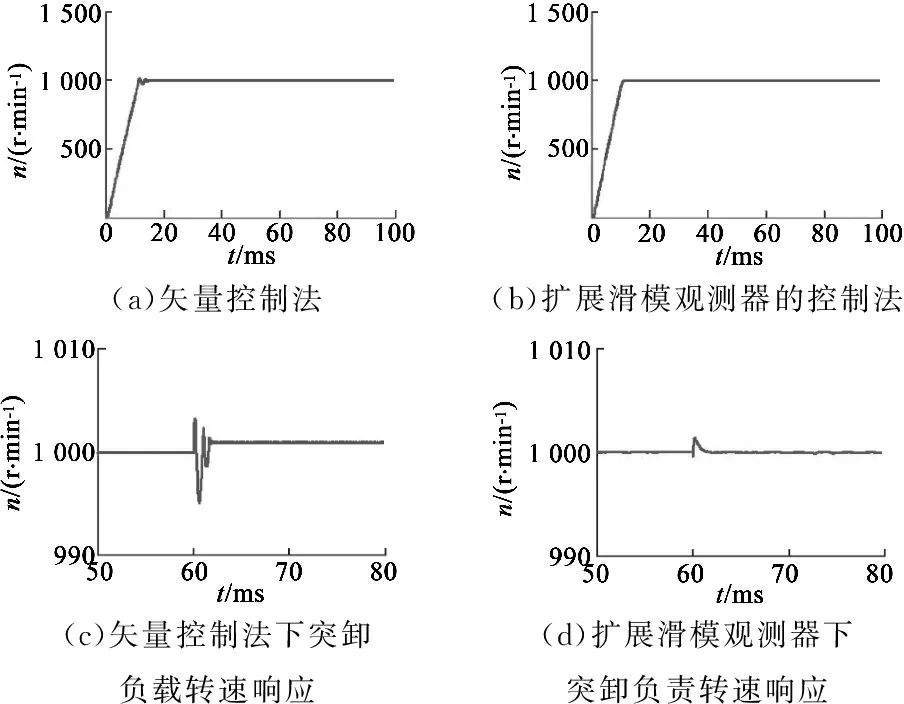
(a)矢量控制法(b)扩展滑模观测器的控制法(c)矢量控制法下突卸负载转速响应(d)扩展滑模观测器下突卸负责转速响应

图3 两种控制方式转速响应对比曲线

通过仿真结果可以看出，当采用矢量控制方法时，系统转速有明显波动，且存在稳态误差；而采用扩展滑模观测器的控制法时，系统转速更加平稳，具有较强的抗外界干扰能力，鲁棒性更好。

5 结 语

本文针对PMLSM在速度跟踪控制过程中因其模型具有非线性、参数时变性以及变量间的随机耦合等特点，导致电机速度跟踪控制精度低，提出了一种滑模观测器的PMLSM反馈线性化速度跟踪控制方法。通过解耦处理，将电机电流和速度子系统解耦成相互独立的系统，设计了速度跟踪控制器，对反馈线性化所需要的动子加速度以及负载扰动信号设计了一种扩张滑模观测器对其进行有效观测。仿真结果表明，在基于滑模观测器的反馈线性化方法下，永磁同步电动机起动转速具有很小的超调量和上升时间；而当出现负载的突然增加和减小时，在滑模观测器的反馈线性化方法下电机转速和转矩响应波动更小，具有较好的动态特性，抗外界扰动能力强，鲁棒性好。

[1] 王鑫, 李伟力, 程树康. 永磁同步电动机发展展望[J].微电机,2007,40(5):69-72.

[2]ANDONVT,GIUSEPPELC,VINCENZOG,etal.Slidingmodeneuro-adaptivecontrolofelectronicdrives[J].IEEETransactionsonIndustrialElectronics,2007,54(1):671-679.

[3] 张国柱,陈杰,李志平.直线电机伺服系统的自适应模糊摩擦补偿[J].电机与控制学报,2009,13(1):154-160.

[4]MOHAMEDYARI,EI-SAADANYEF.Acurrentcontrolschemewithanadaptiveinternalmodelfortorquerippleminimizationandrobustcurrentregulationinpmsmdrivesystems[J].IEEETransactionsonEnergyConversion,2008,23(1):92-100.

[5]CHANGSH,CHENPY,TINGYH,etal.Robustcurrentcontrol-basedslidingmodecontrolwithsimpleuncertaintiesestimationinpermanentmagnetsynchronousmotordrivesystems[J].ElectricPowerApplication,IET,2010,4(6):441-450.

[6] 张月玲,党选举.基于死区迟滞函数的永磁同步直线电机滑模控制[J].中国电机工程学报,2011,31(3):67-74.

[7] 曹先庆，朱建光，唐任远．基于模糊神经网络的永磁同步电动机矢量控制系统[J]．中国电机工程学报，2006，26(1):137-141．[8] UTKIN V I.Variable structure systems with sliding modes[J].IEEE Transactions on Automatic Control, 1997, 22(2): 212-222.

[9] 张家明,卢京潮.积分滑模控制在飞控中的应用[J].系统仿真学报,2009,21(13):4069-4071.

[10] BAI K I C,KIM K H,YOUN M J.Robust nolinear speed control of PM synchronous motor using boundary layer integral sliding mode control technique[J].IEEE Transactions on Control Systems Technology, 2000, 8(1): 47-54.

[11] 陈伯时,徐荫定.电流滞环控制PWM逆变器异步电动机的非线性解耦控制系统[J]自动化学报,1994,20(1):50-56.

[12] 曹建荣.基于逆系统理论的感应电机解祸控制的研究[J].电工技术学报,1999,14(1):7-11.

[13] 刘保彬，周伟．永磁同步电动机的自适应反推控制[J]．中小企业管理与科技， 2010，3(6):17-18．

[14] 汪军， 王文．基于线性反馈法的永磁同步电机混沌控制[J].大连交通大学学报，2010，31(4):50-52.

Speed Control of Permanent Magnet Linear Synchronous Motor Based on Sliding Mode Observer

ZHANGLiang,XUAo-ra,BAIDi,GUCai-lian,WANGYue-zhi

(Shenyang Institute of Engineering,Shengyang 110136,China)

For the low control accuracy of permanent magnet linear synchronous motor during in the speed tracking control process as the model is nonlinear, parameter variability and variable random coupling characteristics, a synovial observer for permanent magnet linear synchronous motor feedback linearization speed-tracking control method was put forward. First the nonlinear model of permanent magnet linear synchronous motor was established, using non-linear coordinate transform and nonlinear state feedback to decouple the motor system, and the independent current and speed subsystems with nonlinear characteristics were gotten. The speed tracking controller was designed, and the extended synovial observer was designed for rotor acceleration speed and load disturbance signal that feedback linearization needs. Simulation results show that the control method can greatly improve the accuracy of motor speed tracking with better robustness.

permanent magnet linear synchronous motor (PMLSM); speed tracking control; synovial observer; stability

2015-08-11

TM359.4；TM351

A

1004-7018(2016)01-0051-04

张亮(1992-)，男，助理工程师，研究方向为从事电力系统及其自动化。