带整流负载的六相方波永磁发电机建模仿真
2016-12-06李明昊
周 石,李明昊,周 羽
(海军工程大学,武汉 430033)
带整流负载的六相方波永磁发电机建模仿真
周 石,李明昊,周 羽
(海军工程大学,武汉 430033)
建立一个普适的发电机数学模型可以有效地帮助人们了解和优化发电机性能。首先简述了六相方波永磁发电机的定转子结构,计算了电机的电感矩阵,利用解析法建立了电机的基本数学方程,然后将电机与整流负载联系起来,共同建立了系统方程。通过系统方程,在MATLAB纯代码环境下建立整个系统的数学模型,并进行仿真计算。最后将仿真计算结果与原理样机实验数据对比,确认了所建立模型的正确性和有效性。
整流负载;六相方波永磁发电机;电感矩阵;数学模型;仿真
0 引 言
在分布式发电领域,使用多相发电机能够方便有效地提高用电品质。相比于传统三相电机,多相电机能够大幅减小气隙磁场的谐波含量,从而使电机性能得到改善,也使全系统的可靠性和稳定性得到提升[1]。六相电机作为最早被提出的多相电机,已经得到广泛的应用。
方波发电机在交-直变换系统中,由于其能提供稳定的外电压、外电流,可以有效地降低负载电流脉动。而且对方波电机结构的优化,可以更有效地利用铁心。在铜损相同的情况下,提供更大的输出功率[2]。
相对于电励磁结构发电机,永磁发电机由于省却了励磁绕组和电刷,大大简化了电机结构,提升了电机可靠性,并减小电机的体积、重量。永磁体作为励磁源,减小铜耗,提高了发电机的效率[3-5]。这些特性使得永磁发电机很适合用于分布式发电领域。
然而,六相永磁发电整流系统由于其绕组数的增加,各绕组间的耦合关系相对比较复杂,整流器的导通情况的非连续性,得到其工程适用的数学模型并非易事。尽管如此,人们仍然希望找到合适的数学模型,以便更深入地发挥六相永磁发电机的长处[6]。文献[7]利用Park方程,基值变换,等效三相同步电机给出了计算六相双Y同步电动机参数的方法。文献[8]采用傅里叶级数法计算了表贴式双三相永磁同步电机的电磁性能,建立了解析模型,并与有限元结果对比,确定了解析法的准确性。文献[9]在Simulink环境下建立了六相凸极永磁同步电机——变流器系统的仿真模型,文献[10]同样也是在Simulink环境下建立六相永磁同步发电机的模型。为了深入研究六相永磁发电机整流系统的各项特性,必须对整个系统有更仔细的分析,以建立更准确的模型。
本文研究的是一台3对极36槽无阻尼绕组六相方波永磁发电机,两个Y之间相移30°。文中计算了六相永磁发电机的电感矩阵,根据发电整流系统的拓扑结构,提出了一种全解析的六相永磁发电整流系统的数学模型。
1 系统模型建立
1.1 永磁发电机的基本方程
采用一般电机假设和发电机的正向规定惯例[11],建立abc自然坐标下的磁链和电压方程。
磁链方程:
电压方程:
故可得到端电压:
(1)
式中:ψabc=[ψa1,ψb1,ψc1,ψa2,ψb2,ψc2]T为各相绕组的磁链;iabc=[ia1,ib1,ic1,ia2,ib2,ic2]T为各相电流;Uabc=[Ua1,Ub1,Uc1,Ua2,Ub2,Uc2]T为各相端电压;ψfmabc为永磁体在各相绕组中产生的磁链。
永磁发电机无阻尼绕组,电机绕组电感矩阵:
(2)
式中:Lxy=Lyx,Lxx为x相绕组的自感,Lxy为x与y相绕组之间的互感。L是对称矩阵。由于此电机没有阻尼绕组,电感矩阵中只含有定子绕组的电感,且与转子位置无关,所有电感为确定的常数。
电机绕组内阻矩阵r=diag[ra,ra,ra,ra,ra,ra]。
(3)
1.2 反电动势
方波电机由于其反电动势顶端较平整,因而当用在整流系统中,输出直流侧可以得到非常平整的直流电压,这样可以有效地降低直流侧的谐波,对直流负载停供更高品质的电力。方波永磁发电机由于其励磁是由永磁体提供,所以其反电动势的形状完全由永磁体的形状与充磁方向决定。在实践中,反电动势并不是标准的方波,常见的反电动势的形状一般呈现梯形波的形状。
为了对方波永磁发电机进行数学建模,反电动势也是重要的参数之一。常见的获取反电动势的方法有三种:一、根据永磁体的形状与充磁方向,定、转子的结构直接计算[12];二、利用有限元软件建立电机剖面二维模型进行计算;三、直接测量样机反电动势,利用数学离合等方法获取反电动势波形。
1.3 电感矩阵
如何获取电机的电感矩阵是电机建模中至关重要的问题,准确地得到电感参数将会决定电机建模的准确性。双Y移30°六相永磁发电机的定子部分绕组如图1所示。
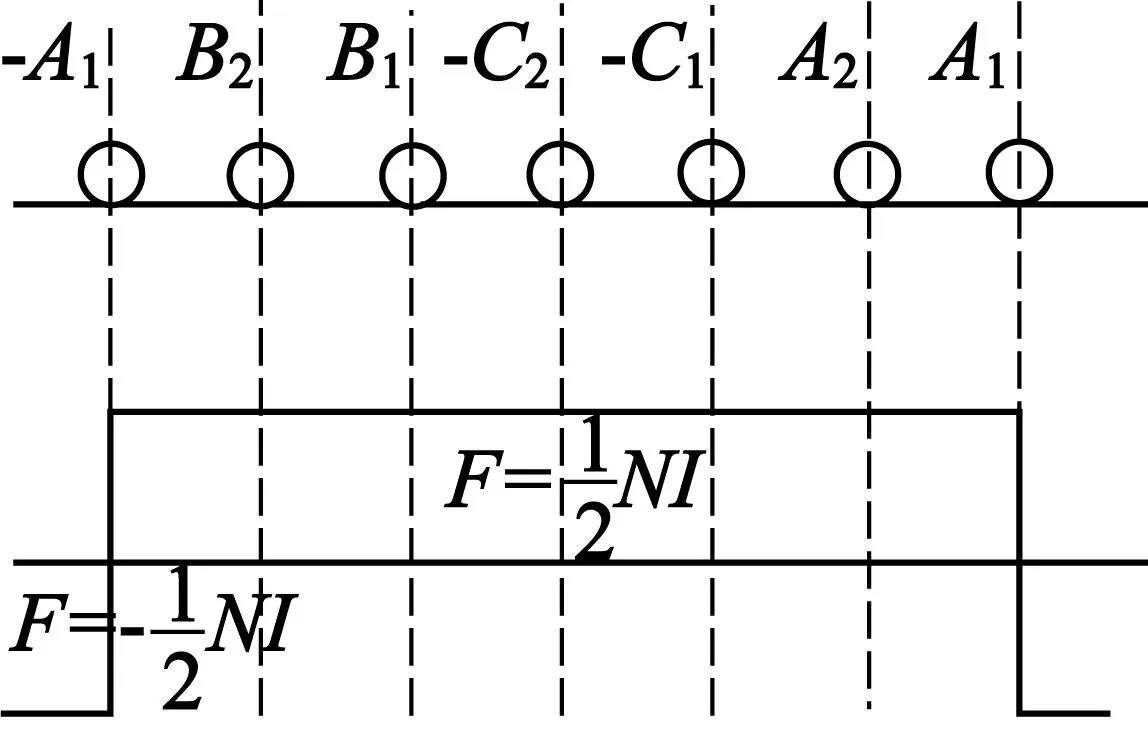
图1 双Y移30°六相PMSM的定子绕组示意图
(4)
故可得到A1相自感:
(5)
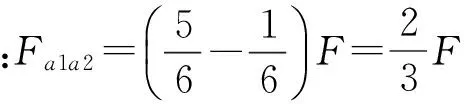
(6)
同理可得到:
(7)
由于L是对称矩阵,故可得到完整的电感矩阵L。
1.4 槽漏感
上述电感矩阵并不包含漏感,然而此种电机的槽漏感对电机性能的影响非常大,因此不能简单地利用修正系数,而需要对其有仔细的分析。槽漏感是指绕组中的电流在槽中产生磁场能量的电感。该磁场并未对气隙磁场产生任何影响,但会对绕组中的反电动势造成一定的影响,对相电流产生较大的影响。
由于绕组是集中整距,因此该电机并没有槽互漏感,所以只考虑槽自漏感。
对槽体进行分析,槽形如图2所示。
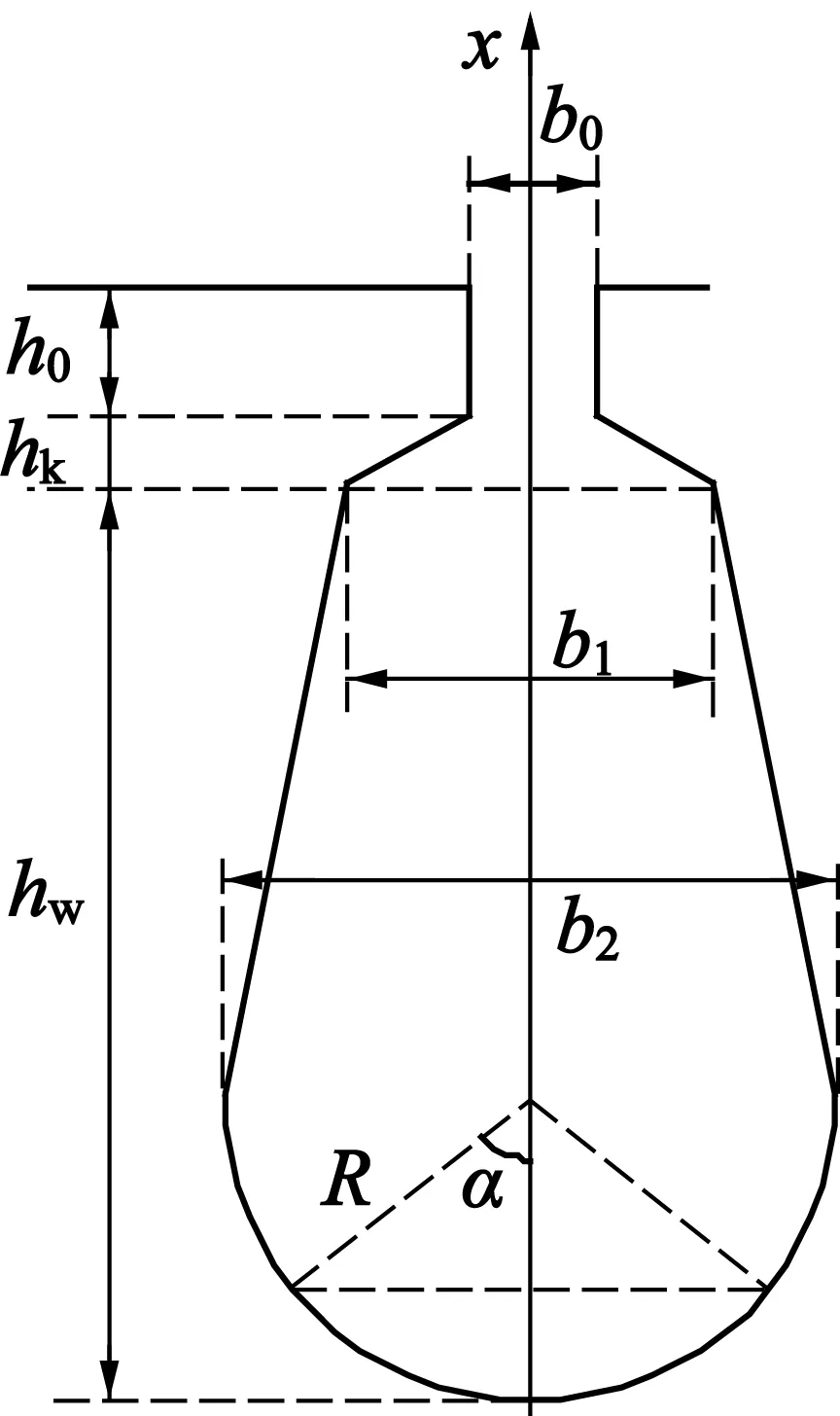
图2 定子槽示意图
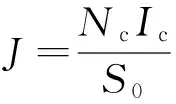
(8)
为计算Wm,沿x方向将槽分成0~R,R~hw,hw~hk,hk~h0四个部分分别进行积分,记为Wm1,Wm2,Wm3,Wm4。
(9)
最后可得:
(10)
电感矩阵式(2)修正:
(11)
1.5 整流负载方程
六相永磁发电机通过不控整流带有反电动势的阻感性负载,如图3所示。
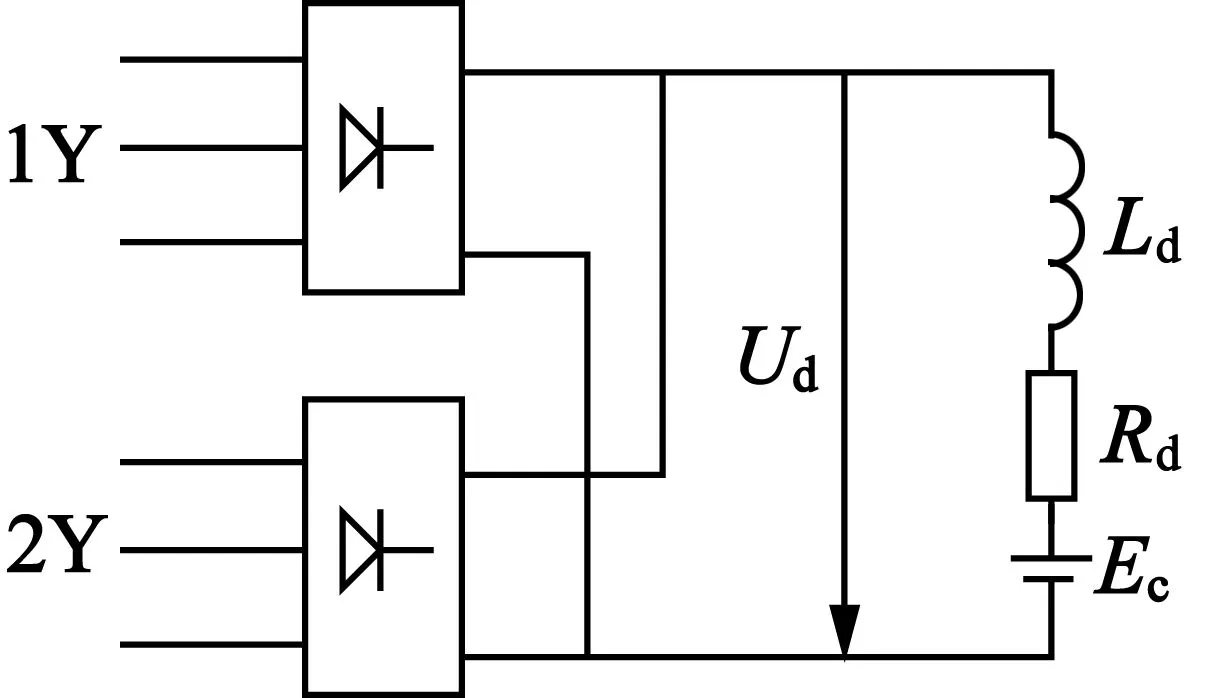
图3 整流负载示意图
负载端电压方程:
(12)
式中:Ud为整流器直流侧电压;id为直流侧电流;Ld为负载电感;Rd为负载电阻;Ec为负载反电动势。
1.6 导通矩阵
两个Y绕组整流后并联向反电动势负载供电,各个Y绕组的导通情况取决于各自绕组的线电压与Ud的关系。引入导通模式矩阵,简称导通矩阵,由导通矩阵可方便地建立起电机绕组回路与外电路的联系。导通矩阵的生成步骤如下:
设定基本矩阵:
(13)
由基本矩阵Db与绕组电压Uabc相乘,判断其各元素与Ud的关系,考虑整流管稳态管在下降时,其判断式:
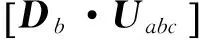
1.7 系统方程
导通矩阵Dk表征了电机定子绕组导通情况。
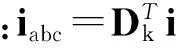
将负载电压方程式(11)扩展到k维,得到:
(14)
式中:(Ud)k×1为元素都是Ud的k行1列矩阵;(Ec)k×1同理;(Ld)k×k为元素都是Ld的k行k列方阵,(Rd)k×k同理。
考虑到电源负载平衡,可得到方程:
(15)
代入式(3)和式(14)化简可得到系统方程:
(16)
2 模型验证
为验证该模型,在MATLAB下搭建了该六相方波永磁发电机的数学模型。为了减小迭代误差,使用四阶龙格-库塔法进行仿真计算。为验证所述理论的正确性,并在本文上述原理样机上进行了实验,样机参数如表1所示,实验现场如图4所示。

图4 实验现场
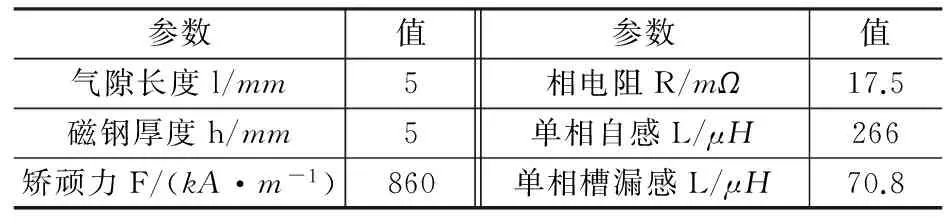
表1 方波永磁发电机基本参数
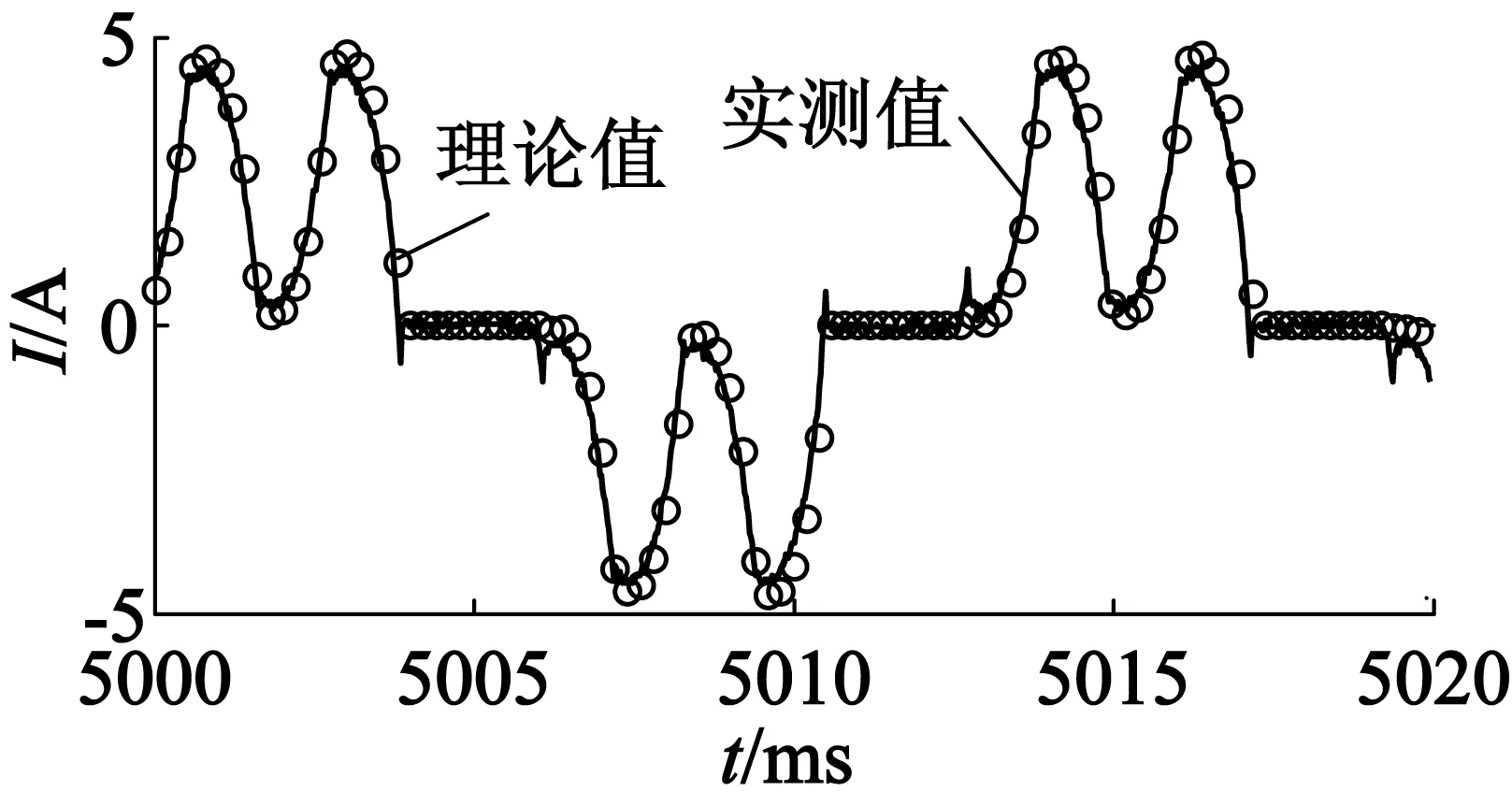
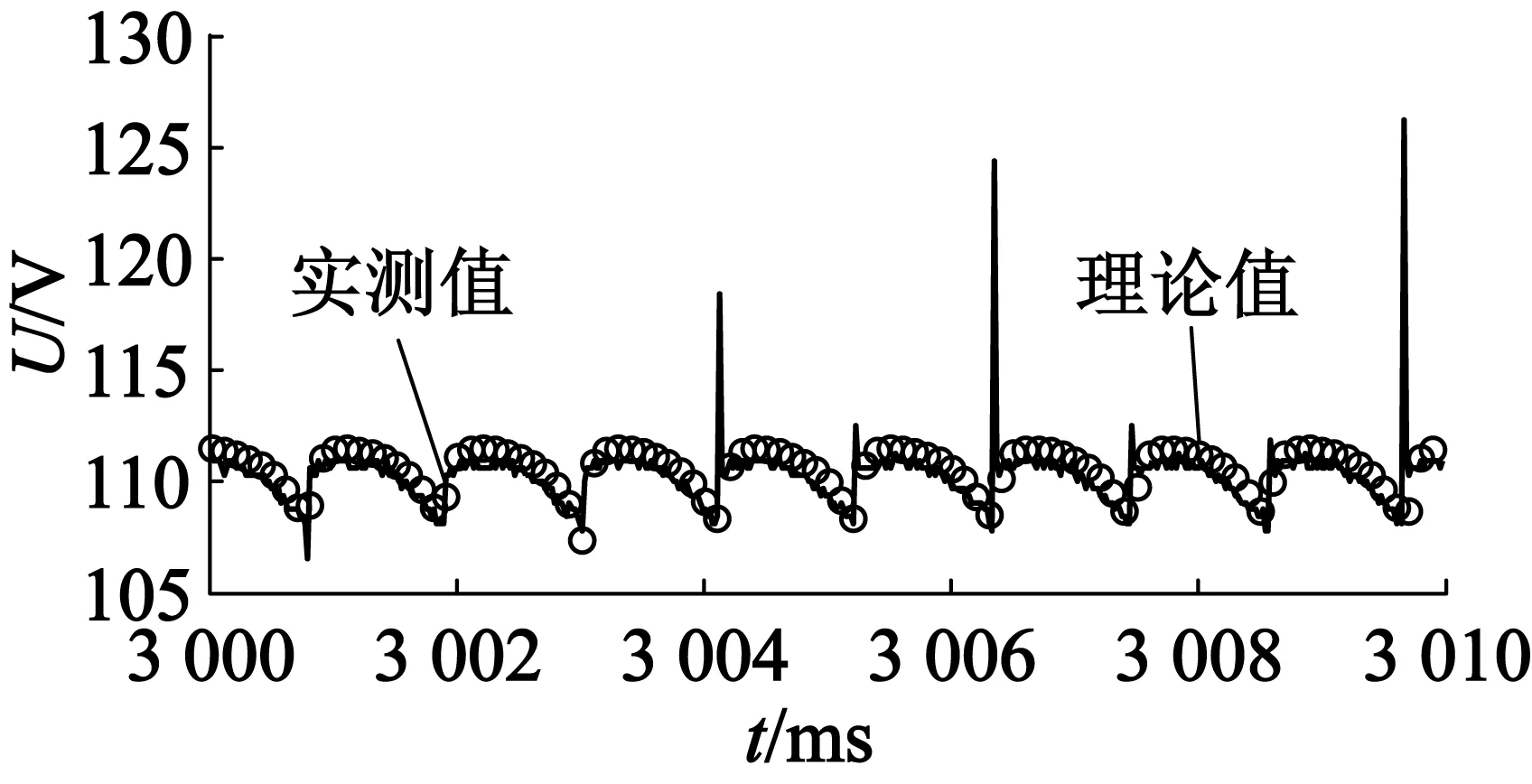
在恒定转速不同的负载下分别记录了电机的相电压、相电流、整流侧直流电压与整流侧直流电流波形,实验数据与仿真结果基本一致。图5是稳态相电压波形对比,图6是稳态相电流波形对比,图7是稳态整流后负载端电压对比,图8是稳态整流后负载端电流对比,所有的结果都很吻合。
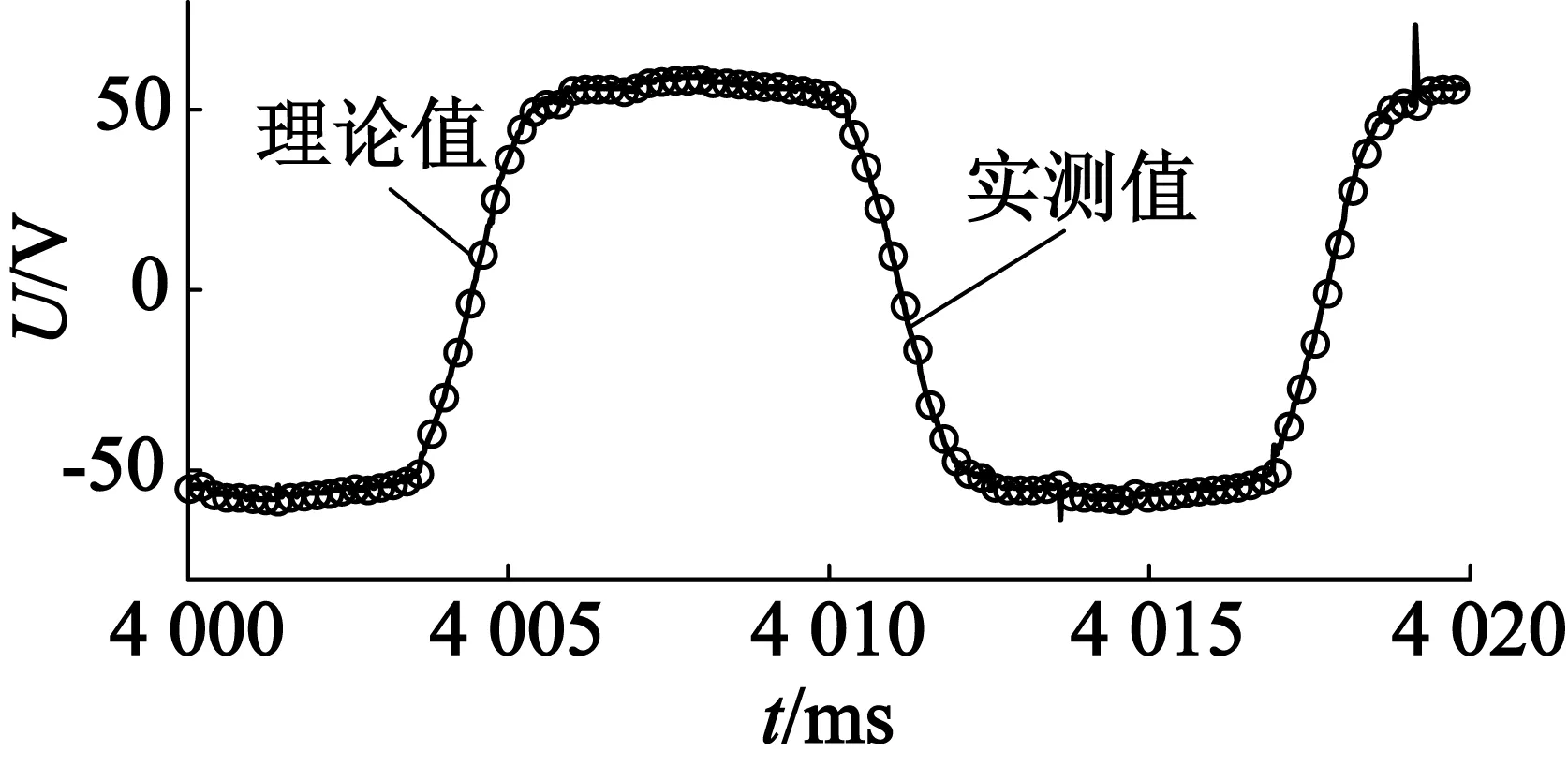
(a) 负载23.5 Ω
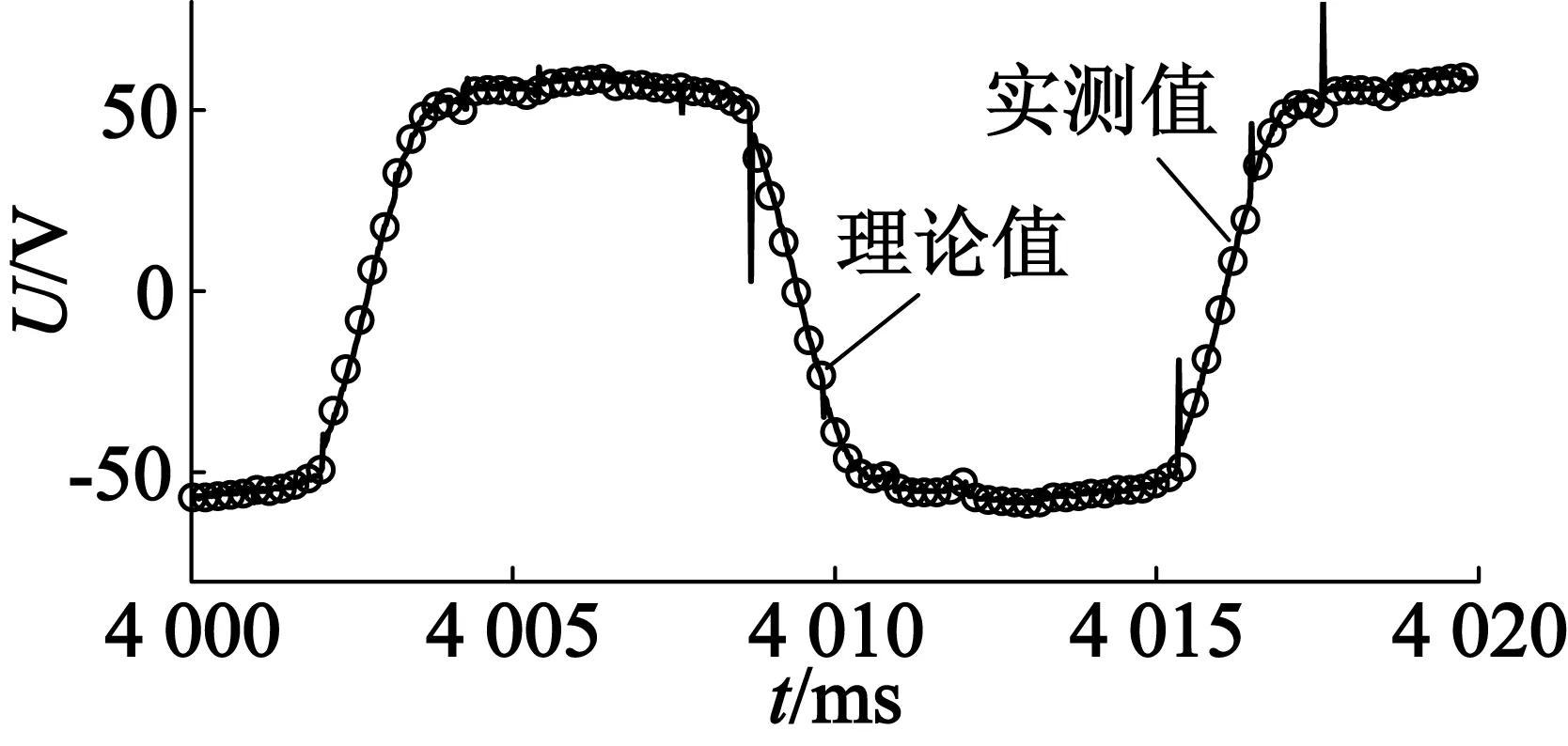
(b) 负载11.9 Ω
(a) 负载23.5 Ω

(b) 负载11.9 Ω
(a) 负载23.5 Ω
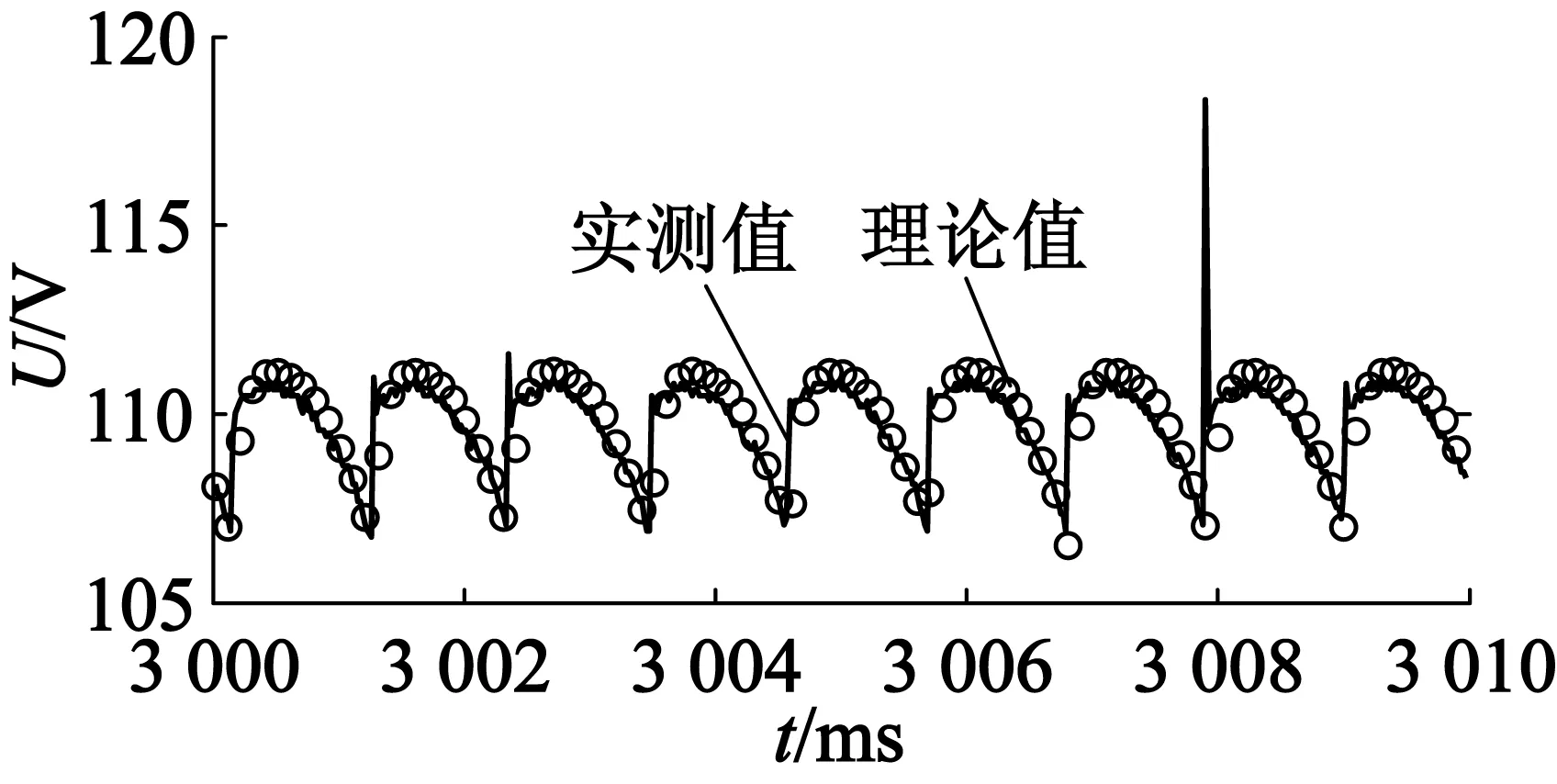
(b) 负载11.9 Ω
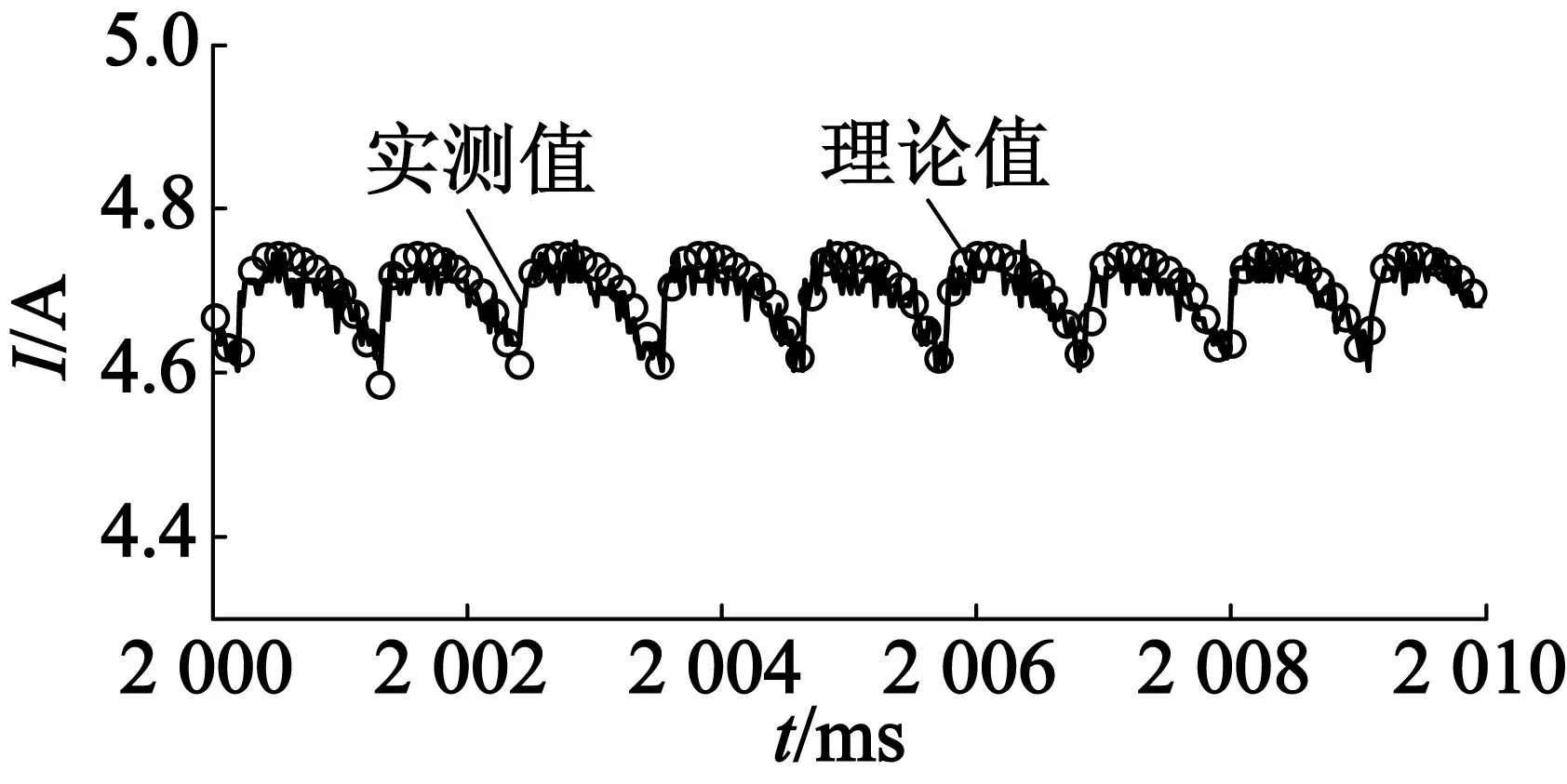
(a) 负载23.5 Ω
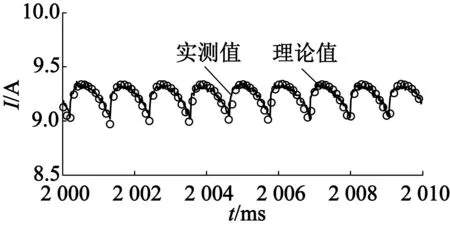
(b) 负载11.9 Ω
综合上述实验验证结果,可以说明本文所给出的理论分析方法和解析模型是正确有效的。
由于多种类别的多相电机的定子绕组结构是类似的,因而本文所使用的等效方法可以用到其它多相永磁电机中去。
3 结 语
(1)利用定义计算了电机的电感参数,并利用整流电路拓扑结构,建立整流导通矩阵。
(2)利用整流导通矩阵将电机与整流负载统一起来,建立完整的六相永磁发电整流系统的系统方程,即系统解析模型。
(3)利用MATLAB仿真、原理样机实验等手段,对本文所提出的解析模型进行了验证,证实了所建立模型的正确性与有效性。
[1] 欧阳斌,晏明,马伟明,等.40°双九相同步电机数学模型研究[J].中国电机工程学报,2015,35(1):206-213.
[2] 张西虎,朱震莲.磁方波电机及其控制[J].微特电机,1993,21(5):39-41.
[3] 骆继明,孔婉琦,黄明明,等.一种磁通切换型永磁同步发电机并网控制方法研究[J].微特电机,2015,43(5):1-3.
[4] 周羽,李槐树,胡绪昌.电流型多相永磁同步电动机调速系统建模与仿真[J].微特电机,2009,37(2):20-26.
[5]ZHOUYu,LIHuaishu,ZHOUShi,etal.Analyticalcalculationofmagneticfieldandcoggingtorqueinsurface-mountedpermanent-magnetmachinesaccountingforanyeccentricrotorshape[J].IEEETransactionsonIndustrialElectronics,2015,62(6):3438-3447.
[6] 范子超,于庆广,张晓明.双定子绕组同步电机及其单绕组等效模型[J].电工技术学报,2007,22(2):2-8.
[7] 汤广福,傅鹏.六相双Y同步电机等效电路及其参数的确定[J].中小型电机,1997,24(2):17-28.
[8] 郭思源,周理兵,齐歌.双三相永磁同步电机电磁性能解析计算[J].电工技术学报,2014,29(5):17-28.
[9] 王舰威,张凯.用于分布式发电的六相永磁同步电机仿真建模[J].船电技术,2013,33(3):57-60.
[10] 汪远林,窦满峰.六相永磁同步发电机的整流稳压电路仿真[J].微电机,2012,45(8):46-49.
[11]ZHANGGaifan,MAWeiming.TransientAnalysisofSynchronousMachines[M].Wuhan:HubeiScienceandTechnologyPress,2001.
[12]ZHOUYuZhou,LIHuaishu,WANGWei,etal.Improvedmethodforcalculatingmagneticfieldofsurface-mountedpermanentmagnetmachinesaccountingforslotsandeccentricmagnetpole[J].JournalofElectricEngineeringandTechnology,2015,10(3):2015.
Modeling and Simulation of Six-Phases Trapezoidal Permanent Magnet Generator with Rectifying Load
ZHOUShi,LIMing-hao,ZHOUYu
(Naval University of Engineering, Wuhan 430033, China)
A general suitable mathematical model gives people an easy access to knowing and development the performance of permanent magnet generator. Structure of the six-phases trapezoidal permanent magnet generator was briefly presented, then the inductance matrix and an analysis mathematical model were given in this article. Combining with rectifying load, a system equation was presented. With this equation, simulation was done in MATLAB with pure code. Compared to the experimental data of prototype, the model was verified in the end.
rectifying load; six-phases trapezoidal permanent magnet generator; inductance matrix; mathematical model; simulation
2015-04-22
TM313
A
1004-7018(2016)01-0007-05
张智华(1983-),男,讲师,硕士,研究方向为电机控制技术。
